一道高考导数压轴题的解法探究及背景和推广
刘 冰
(厦门外国语学校石狮分校,福建 厦门 362700)
2023年高考数学新课标Ⅱ卷的导数压轴题,第(1)问考查的是证明不等式,构造函数即可解决.而第(2)问考查的是已知函数f(x)的极值点,求参数a的取值范围,有一定的难度.其难点主要在于对参数a的讨论以及对极值的判断与取点上.该试题很好地考查了考生的分类讨论思想和数学运算、逻辑推理等素养.
1 真题再现
2023年高考数学新课标Ⅱ卷第22题如下:
(1)证明:当0 (2)已知函数f(x)=cosax-ln(1-x2),若x=0是f(x)的极大值点,求a的取值范围. (1)先证:当0 设g(x)=x-sinx,x∈(0,1),则g′(x)=1-cosx>0,所以g(x)在(0,1)单调递增,g(x)>g(0)=0,即sinx 再证:当0 解法1利用x>sinx.设h(x)=x2-x+sinx,x∈(0,1),由x>sinx,得 所以h(x)在(0,1)单调递增,故h(x)>h(0)=0,即x-x2 解法2两次求导.设h(x)=x2-x+sinx,x∈(0,1),则h′(x)=2x-1-cosx,h″(x)=2-sinx.当0 (2)解法1令1-x2>0,解得-1 若a=0,则f(x)=-ln(1-x2),x∈(-1,1), 因为y=-lnu在定义域内单调递减,y=1-x2在(-1,0)上单调递增,在(0,1)上单调递减,则f(x)=-ln(1-x2)在(-1,0)上单调递减,在(0,1)上单调递增,故x=0是f(x)的极小值点,不合题意,所以a≠0. 当a≠0时,令b=|a|>0,因为 f(x)=cosax-ln(1-x2)=cos(|a|x)-ln(1-x2)=cosbx-ln(1-x2), 且f(-x)=cos(-bx)-ln[1-(-x)2]=cosbx-ln(1-x2)=f(x), 即当x∈(0,m)⊆(0,1)时,f′(x)>0,则f(x)在(0,m)上单调递增,结合偶函数的对称性可知,f(x)在(-m,0)上单调递减,所以x=0是f(x)的极小值点,不合题意[1]. 因为x=0是f(x)的极大值,由函数的连续性,我们知道还需满足在x=0的左侧附近,f′(x)>0,在x=0的右侧附近,f′(x)<0.由题意易得,f(x)是关于x的偶函数,也是关于a的偶函数, 因此只需要关注x∈(0,1),a>0的情况. 本题的高数背景是极值的第二充分条件和第三充分条件.合并后即是如下定理. 定理设函数f(x)在U(x0,δ)内n阶可导,且 f′(x0)=f″(x0)=…=f(n-1)(x0)=0,f(n)(x0)≠0,则 (1)当n为奇数时,f(x)在点x0不取极值; (2)当n为偶数且f(n)(x0)>0时,f(x)在x0取极小值; (3)当n为偶数且f(n)(x0)<0时,f(x)在x0取极大值. 利用定理,可得到本题的另一解法. 解法3S表示f(x)的极大值点的集合,则 由定理可得: 本题还可以作如下推广 . (1)证明:当0 (2)已知函数f(x)=cosax-aln(1-x2),若x=0是f(x)的极大值点,求a的取值范围[2]. 解(1) 略. (2)显然f(x)的定义域是I=(-1,1).易见x∈I时 f″(0)=2a-a2; f‴(0)=0; f(4)(0)=a4+12a. 设S表示f(x) 的极大值点的集合. 由定理可得: 若0 若a<0或a>2,则f′(0)=0,f″(0)<0,0∈S; 若a=2,则f′(0)=f″(0)=f‴(0)=0,f(4)(0)>0,0∉S; 若a=0,则f(x)=1为常数,0∉S. 综上,a的取值范围为(-∞,0)∪(2,+∞). 试题以三角函数、对数函数为背景.三角函数的导数是中学数学教学的重点与难点.试题巧妙地将三角函数与对数函数相结合,讨论函数的极值问题,具有一定的综合性.试题的高等数学背景是极值的第三充分条件,起点高,但落点低,设计新颖,紧扣课程标准.通过第(1)问铺设好的不等式,给第(2)问的证明提高了思路,降低了思维强度.2 解法探究







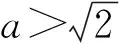

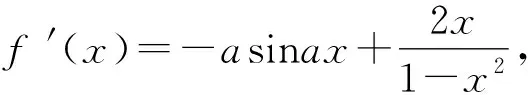

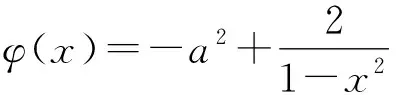


3 背景分析
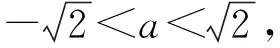



4 试题推广

