三种非线性时变识别方法的对比研究

陈长龙 刘启方

摘要：

利用2021年日本福岛地震（MJMA 7.3）中6个KiK-net台站的观测记录，分别基于移动窗解卷积法、移动窗谱比法和移动窗自相关函数法对场地非线性时变过程进行研究，分析非线性发生的阈值和程度。研究表明：三种方法识别场地非线性时变特征的稳定性不同。移動窗解卷积法更容易获得较为稳定的土体非线性时变过程，但其反映的是地表至井下平均波速的变化，识别的非线性程度偏低。对于存在强波阻抗比的浅表层土体，移动窗谱比法和移动窗自相关函数法识别的非线性程度更强;对于较低波阻抗比的浅表层土体，则不容易识别出稳定的非线性时变结果。三种方法识别的非线性最强时刻基本一致，皆位于整条记录加速度峰值附近。基于三种方法识别的6个台站的非线性阈值约在40～140 gal，剪切波速下降比在16%～53%之间，场地非线性程度较明显。

关键词：

移动窗解卷积; 移动窗谱比; 自相关函数; 场地非线性; 时变

中图分类号： P631      文献标志码：A   文章编号： 1000-0844（2023）02-0372-10

DOI：10.20000/j.1000-0844.20211110002

Comparative study on three identification methods of the nonlinear time-

varyin  process： a case study of the 2021 Fukushima earthquake in Japan

CHEN Changlong， LIU Qifang

（Suzhou University of Science and Technology， Suzhou 215011， Jiangsu， China）

Abstract：

Based on the records of six KiK-net stations in the 2021 Fukushima earthquake （MJMA7.3）， the nonlinear time-varying process of the site was studied using the moving-time-window deconvolution method， moving-time-window spectral ratio method， and moving-time-window autocorrelation function method. Then， the threshold and degree of nonlinearity were analyzed. Results show that the ability of the three methods to identify the nonlinear time-varying characteristics of the site differs. The moving-time-window deconvolution method can easily obtain a more stable nonlinear time-varying response for soil， but the degree of nonlinearity is low. The method reflects the change of average wave velocity from the surface to the underground. For shallow soils with a strong wave impedance ratio， the nonlinear degree of identification results derived from the moving-time-window spectral ratio method and moving-time-window autocorrelation function method are strong. These two methods cannot provide stable nonlinear time-varying results of shallow soils with a low wave impedance ratio. The strongest nonlinear moments identified by the three methods are basically the same and are located near the peak acceleration of the whole record. The nonlinear threshold values of the six stations identified by the three methods are about 40-140 gal， and the shear wave velocity drops between 16% and 53%， indicating that the degree of site nonlinearity is high.

Keywords：

moving-time-window deconvolution; moving-time-window spectral ratio; autocorrelation function; site nonlinearity; time-varying

0 引言

场地非线性是地震工程领域的研究热点，土体在强震动作用下会产生损伤，从而导致应变幅值增加，剪切模量降低及阻尼比增强［1-7］，非线性发生的阈值、程度及恢复过程均是场地非线性研究的主要问题。目前，基于强震动观测数据直接分析场地非线性的方法主要有谱比法［2-3］、广义反演法［8］、S变换法［9］、地震干涉测量法［10］和自相关函数法［11］等。这些传统分析方法一般是利用主震之前的小震记录确定场地处于线性状态时的水平，利用主震记录确定非线性状态时的水平，利用余震记录分析非线性恢复情况。基于以上方法，研究人员判断的不同场地非线性阈值差别较大［1-3］，在100～300 gal之间，非线性的恢复过程也有很大差异，既有震后几分钟甚至更短时间内恢复［10］，也有需几年恢复［2，12］。另外，研究人员还提出了一些非线性程度指标［5，13-14］（DNL、ADNL、PNL等）。

场地经历的强地震动一般会从较低幅值逐渐增加到较高的震动水平，然后再降低到弱震动水平。因此可根据一条强震记录作用下不同时段场地的反应，获得场地土的非线性时变特性。近十几年来，研究人员将移动时间窗技术与传统分析方法结合，提出了移动窗谱比法、移动窗解卷积法和移动窗自相关函数法等，针对一条记录分析不同时间窗内非线性程度的变化，从而获得非线性时变特性。如Wu等［15］ 利用移動窗解卷积法，针对2011 Tohoku 地震（MW9.0）KiK-net台网中6个台站主震记录的分析表明，场地共振频率明显下降，等效剪切波速最大下降到主震前的70%。Sawazaki等［16］利用移动窗谱比法和2000年日本Western-Tottori地震（MW6.7）的主震记录，对KiK-net台网的SMNH01台站场地土的分析表明，在峰值加速度最大值（PGA）附近，剪切模量下降到主震前的52%，等效剪切波速下降30%。Wu等［17］利用移动窗谱比法对KiK-net 台网中6个台站1999年1月至2008年5月2 204个地震的观测记录分析表明，PGA在60～100 gal时场地发生非线性反应，明显低于传统方法的结果。Federico等 ［18］ 利用移动窗解卷积法和2011 Tohoku 地震（MW9.0）主震记录，分析了IBRH16台站土体剪切模量的时变特性，Bonilla等［19］则进一步利用该台站同一记录，分析了自相关函数法和移动窗解卷积法在识别非线性时变特性的差异，结果表明，两种方法均可有效识别出场地非线性的发展过程，但自相关函数法获得的非线性程度大于移动窗解卷积法，且非线性恢复速度更快。

为了分析移动窗解卷积法、谱比法和自相关函数法在识别场地非线性时变特性的差异，本文从KiK-net台网中选择6个台站，其中4个台站的表层与下卧基岩波阻抗比很大，另外2个台站土层波速则由表层向下逐渐增大，无强波阻抗比分界面。利用2021年日本福岛地震（MJMA7.3）中接收到的主震记录，分析三种方法对于这两类不同场地的非线性时变特性识别的差异和可行性。

1 数据选取

2021年2月13日23时8分日本福岛县东部近海地区发生7.3级地震，震源深度约为55 km，震中位于（37.728°N，141.698°E），日本防灾技术研究所（NIED）所属的KiK-net台网有超过384个台站记录到了完整的主震记录。此次地震与2011年东日本大地震（MW9.0）的震中距离约75 km，是2011年东日本大地震的余震［20］。本文选择获得此次地震主震记录的6个台站识别场地的非线性时变特性，图1为台站和震中位置。表1给出了这6个台站的土层地质资料［21］，其中1个台站为C类场地，其余台站均为D类场地，这些台站记录到的地表峰值加速度在300～1 100 gal之间，易发生非线性。其中FKSH17、FKSH18、FKSH19和FKSH11台站存在强波阻抗比的分界面，而FKSH20和MYGH10台站剪切波速变化较平缓。

2 研究方法

本文采用移动窗解卷积法、谱比法和自相关函数法分析场地土的非线性时变特征。移动窗解卷积法是对固定宽度时窗内的地表和井下记录解卷积，获得一个时间窗内的等效剪切波速，然后沿时间轴按一定的窗口距离移动时间窗，获得下一个时间窗内结果［如图2（a）中红色框表示一个时间窗，黑色框为下一个时间窗］。通过计算每个窗口的PGA（亦称为窗内PGA），获得不同时段的土体波速随时间或窗内PGA的变化。根据等效剪切波速的变化，判断土体是否发生非线性及其程度。该方法首先将井下和地表处的地震动记录进行解卷积计算，解卷积结果G（ω）为：

G（ω）=U1（ω）U2（ω）=U1（ω）U*2（ω）U′2（ω）2 （1）

式中：地表和井下加速度记录的傅里叶谱分别为U1（ω）和U2（ω）;* 表示复共轭;分子为地表与井下加速度在频域内的互功率谱，分母为井下加速度的功率谱。为稳定计算，一般采用U′2（ω）对U2（ω）的进行校正：

U′2（ω）2=U2（ω）2;当U2（ω）≥0.1maxU2（ω）

0.1maxU2（ω）2;当U2（ω）<0.1maxU2（ω）（2）

然后对解卷积结果进行傅里叶逆变换，获得井下脉冲输入时地表的响应。通过脉冲响应获得井下台站到地表地震波的传播时间（一般取正或负时间轴上最大值所对应的时刻），利用式（3）计算土体等效剪切波速。

vS=hΔt （3）

式中：vS代表等效剪切波速;h代表井下台站到地表的距离;Δt代表井下台站到地表脉冲波的传播时间。

移动窗谱比法中窗口的选择与移动窗解卷积类似，不同的是通过计算每一时间窗内地表和井下记录傅氏谱比，获得时间窗内的峰值频率，得到峰值频率随时间或窗内PGA的变化。在进行谱比前，一般需要对傅里叶谱进行平滑，本文采用0.5 Hz的帕曾窗进行平滑。通过峰值频率的变化，判断土体是否发生非线性及其程度。设v0和f0是线性状态土体波速和固有频率，某一时间窗内识别的波速和峰值频率为v和f，由于每个时间窗内的峰值频率为其下覆土层的固有频率，正比与土层的波速，则土体波速的变化Δv正比峰值频率的变化Δf［式（4）］，因此，可以通过固有频率的变化判断剪切波速的变化。

Δvv0=Δff0 （4）

移动窗自相关函数法［11］是利用一定时间窗内地表记录进行自相关，从地震事件波形中提取土层某一界面反射波信号，观察时间延迟，由于反射波延时正比于界面之上土层波速，因此可以通过延时的变化计算波速的变化，如式（5）

Δtt=t0-tt0=v0-vv0=-Δvv0 （5）

式中：t0和v0是土层线性状态下延时和波速;t和v是某一时间窗自相关函数法计算的延时和波速;Δt是延时变化;Δv波速变化。

采用这三种方法进行分析时，时间窗宽和窗距的选取是移动窗技术的关键，其直接决定了结果的稳定性和分辨率。时间窗口宽度过窄，会导致结果的不稳定。时间窗口宽度过长，时间分辨率太低，无法很好地反映频谱特性随时间的变化特征。为此，我们参考了相关研究［16-19］，并进行了大量的窗长和窗距测试，最终确定10 s窗长、2 s窗距可获得稳定结果，上述三种方法采用相同的窗长和窗距。为消除截断误差的影响，本文对截取窗口两端采用10%窗口长度的边瓣余弦函数进行处理。由于所有观测记录未滤波的加速度傅氏谱对应的能量主要集中在1～13 Hz范围，本文选择此频段进行滤波。

3 分析与讨论

图2～图7给出了利用移动窗解卷积法、谱比法和自相关函数法识别的4个存在强波阻抗比分界面台站的非线性时变过程。

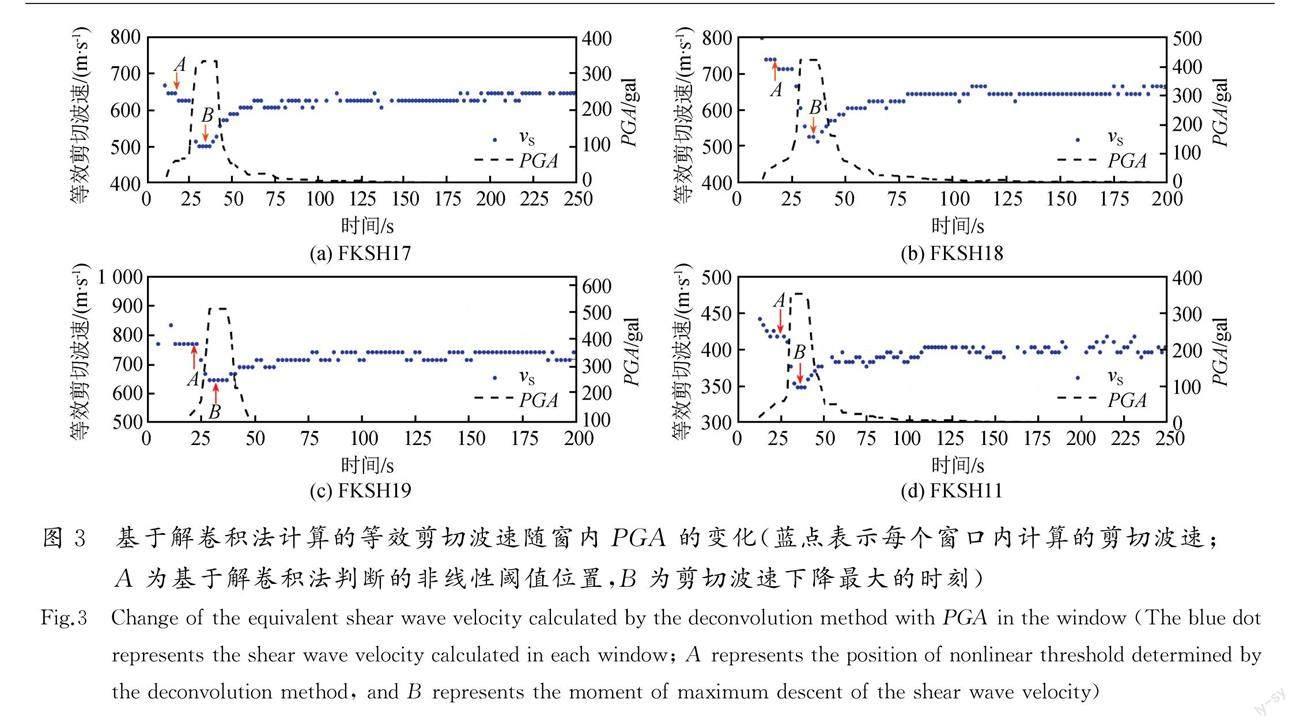
FKSH17台站的钻孔深度100 m，vS30为544 m/s，属于美国NEHRP规范中的C类场地，钻孔资料表明（表1），表层6 m是剪切波速为180 m/s 的砂砾，其下是剪切波速为1 100 m/s的风化花岗岩和花岗岩，两层之间的波阻抗比为9.9（表1），存在强波阻抗比分界面，强波阻抗比分界面之上的土层总厚度为6 m，等效剪切波速为180 m/s。由于风化花岗岩波速较高，非线性很可能主要发生在浅表层6 m的砂砾中，地表的峰值加速度（PGA）为333 gal。三种方法在该台站识别非线性时变过程大致相同，即非线性程度随着窗内PGA的增大而增强，当PGA达到整条记录的峰值时，非线性特征最明显，随着PGA的逐渐减小，非线性逐步恢复。从非线性发生的阈值看，三种方法识别出结果差别不大，在60～70 gal之间。非线性下降程度也基本一致，识别的波速最大下降分别为22%、24%和22%（表2），均位于PGA最大值附近。

FKSH18台站钻孔深度100 m，vS30为307 m/s，属于美国NEHRP规范中的D类场地，表层4 m是剪切波速为140 m/s的风化花岗岩，第二层8 m是剪切波速为220 m/s的风化花岗岩，第三层18 m是剪切波速为550 m/s的风化花岗岩。二三层之间的波阻抗比为3.8。强波阻抗比分界面之上的土层总厚度为12 m，等效剪切波速为185 m/s。地表的PGA为424.8 gal，三种方法识别出的非线性阈值相差不大，在56～66 gal之间。三种方法识别的非线性下降程度不同，识别的波速最大下降为29%、40%和43%（表2），谱比法和自相关法的结果较为接近，且明显大于解卷积法的结果。

FKSH19台站钻孔深度100 m，vS30为338 m/s，属于美国NEHRP规范中的D类场地。表层2 m是剪切波速为170 m/s的表土，第二层18 m是剪切波速为270 m/s的花岗岩，第三层20 m是剪切波速为970 m/s的花岗岩，二三层之间的阻抗比为5.0，强波阻抗比分界面之上的土层总厚度为20 m，等效剪切波速为255 m/s。地表的PGA为513.2 gal，解卷积法和谱比法识别的非线性阈值较接近，分别为141 gal和133 gal，从自相关函数法得到的延时结果看，突变点不明显，不易识别准确结果，本文识别为55 gal，三种方法识别的波速最大下降为16%、28%和23%（表2），仍表现为谱比法和自相关函数法的结果较为接近，且大于解卷积法的结果。

FKSH11台站钻孔深度115 m，vS30为240 m/s，属于美国NEHRP规范中的D类场地，表层1 m是剪切波速为110 m/s 的砾质土，第二层33 m是剪切波速为250 m/s的粉土混砂砾，第三层22 m是剪切波速为1 200 m/s的溶结凝灰岩，二三层之间的波阻抗比为5.2。强波阻抗比分界面之上的土层总厚度为34 m，等效剪切波速为241 m/s。地表的PGV为353.9 gal，三种方法识别非线性时变特性的能力不同，解卷积法和自相关函数法识别的非线性时变特性较明显，识别的非线性阈值分别为59 gal和63 gal，波速最大下降为18%、32%（表2），随着PGA的逐渐减小，波速逐步恢复。但自相关函数法识别的恢复过程振荡较大。而谱比法则几乎识别不出非线性的时变过程，该台站谱比结果在1 Hz、5 Hz、10 Hz处显示3条峰值曲线，但各峰值曲线随时间变化均不明显。

图8给出了利用移动窗解卷积法、谱比法和自相关函数法识别的2个无强波阻抗比分界面台站的非线性时变过程。MYGH10台站钻孔深度205 m，vS30为348 m/s，属于美国NEHRP规范中的D类场地。表层1m是剪切波速为110 m/s 的黏性土，第二层2 m是剪切波速为250 m/s的砂岩，第三层31 m是剪切波速为390 m/s的砾岩和砂岩，第四层80 m是剪切波速为590 m/s的凝灰质砂岩，第五层91 m是剪切波速为770 m/s的砂岩，土层剪切波速逐渐增大，无强分界面。该台站地表PGA很高，达1041.5 gal，值很大。从图8可以看出，三种方法识别出的非线性阈值相差不大，分别识別的阈值为103、93和98 gal。三种方法识别的非线性下降程度不同，识别的波速最大下降为18%、53%和42%，均位于PGA最大值附近。谱比法和自相关函数法的结果较为接近，且显著大于解卷积法的结果，约为2.5～3倍。

FKSH20台站钻孔深度109 m，vS30为350 m/s，属于美国NEHRP规范中的D类场地。表层32 m是剪切波速为350 m/s的腐殖土和砂砾，第二层28 m是剪切波速为500 m/s的砂砾，第三层49 m是剪切波速为610 m/s的砂岩，一二层和二三层的波阻抗比为1.4和1.3，阻抗比较小，剪切波速逐渐增大，无强波阻抗比分界面。地表的PGA为345 gal。从图8可以看出，解卷积法、谱比法分别识别的阈值为39 gal和35 gal，识别的波速最大下降为32%和35%，均很接近。自相关函数法则无法识别非线性时变过程。

从上述分析可见，对于存在强阻抗比分层的4个台站，三种方法识别的阈值总体上差别不大，但在识别非线性程度上，谱比法和自相关函数法的结果较为接近，除FKSH17台站，后两种方法识别的非线性程度均且明显大于解卷积法的结果，这很可能因为谱比法和自相关函数法更容易反映强阻抗比界面之上的浅层波速变化，而解卷积法则反映地表至井下平均波速的变化，由于强阻抗比界面之下的波速较高，非线性程度可能很低（或者不发生），所以平均波速的变化会低于强阻抗比界面之上土层波速的变化。Bonilla等［19］利用获得2011年东日本大地震主震记录的IBRH16台站，分析了自相关函数法和移动窗解卷积法在识别非线性时变特性的差异。结果表明，自相关函数法获得的非线性程度大于移动窗解卷积法，本文结果与其基本一致。

对于无强阻抗比界面的土层，波速随深度变化不明显，因而通过谱比法和自相关函数法不易获得稳定的峰值频率和土层界面的反射波延时，不易获得非线性时变过程。此时解卷积法仍可得到稳定结果，主要由于该方法给出的是井下台站到地表的平均波速，强震动作用下土层平均剪切波速随震动水平的增加仍出现了明显的下降，因此仍可以较好地反映出土层非线性的平均变化，如FKSH20台站。同时我们发现，尽管土层中不存在明显强阻抗比界面，但当场地PGA很高，如MYGH10台站达到1 041.5 gal，三种方法也均能识别出较稳定非线性时变过程。

4 结论

本文利用2021年日本福岛地震（MJMA 7.3）中6个KiK-net 台站的观测记录，分别用移动窗解卷积法、谱比法和自相关函数法分析了场地非线性时变过程，研究表明：

（1） 三种方法识别场地非线性时变特征的稳定性不同。解卷积法更容易获得较为稳定的土体非线性时变过程，但其反映的是地表至井下平均波速的变化，识别的非线性程度偏低。但对于浅表层存在强阻抗比的土体，谱比法和自相关函数法可以获得更强的非线性程度，对于浅表层不存在强阻抗比的土体则不容易识别出稳定的非线性时变过程。三种方法识别的非线性阈值基本上相差不大，对于非线性最强时刻的判定也基本相同，皆位于整条记录加速度峰值附近。

（2） 6个台站地表峰值加速度在300～1 100 gal之间，三种方法识别的非线性阈值在40～140 gal之间，剪切波速下降比在16%～53%之间，表明场地产生较严重的非线性反应。对于PGA最大（1 041.5 gal）的MYGH10台站，剪切波速最大下降达到53%。

本文仅用6个台站初步分析了三种方法的优缺点，由于场地非线性的复杂性，拟在今后的研究中，我们将通过更多的钻井台阵记录，进一步分析上述方法的可靠性和有效性。

参考文献（References）

［1］ BERESNEV I A，WEN U K L.Nonlinear soil response：a reality？［J］.Bulletin of the Seismological Society of America，1996，86（6）：1964-1978.

［2］ WEN K L，BERESNEV I A，YEH Y T.Nonlinear soil amplification inferred from downhole strong seismic motion data［J］.Geophysical Research Letters，1994，21（24）：2625-2628.

［3］ HARTZELL S.Variability in nonlinear sediment response during the 1994 Northridge，California，earthquake［J］.Bulletin of the Seismological Society of America，1998，88（6）：1426-1437.

［4］ 王海云.基于强震观测数据的土层场地反应的研究现状［J］.地震工程与工程振动，2014，34（4）：42-47.

WANG Haiyun.A review of study on soil site response estimating from strong motion data［J］.Earthquake Engineering and Engineering Dynamics，2014，34（4）：42-47.

［5］ 任叶飞.基于强震动记录的汶川地震场地效应研究［D］.哈尔滨：中国地震局工程力学研究所，2014.

REN Yefei.Study on site effect in the Wenchuan earthquake using strong-motion recordings［D］.Harbin：Institute of Engineering Mechanics，CEA，2014.

［6］ 李小军.非线性场地地震反应分析方法的研究［D］.哈尔滨：中国地震局工程力学研究所，1993.

LI Xiaojun.Study on seismic response analysis method of nonlinear site［D］.Harbin：Institute of Engineering Mechanics，CEA，1993.

［7］ 陳学良.土体动力特性、复杂场地非线性地震反应及其方法研究［D］.哈尔滨：中国地震局工程力学研究所，2006.

CHEN Xueliang.Study on soil dynamic characteristics，nonlinear seismic response of complex site and its methods［D］.Harbin：Institute of Engineering Mechanics，CEA，2006.

［8］ REN Y F，WEN R Z，YAMANAKA H，et al.Site effects by generalized inversion technique using strong motion recordings of the 2008 Wenchuan earthquake［J］.Earthquake Engineering and Engineering Vibration，2013，12（2）：165-184.

［9］ BONILLA L F，TSUDA K，PULIDO N，et al.Nonlinear site response evidence of K-NET and KiK-net records from the 2011 off the Pacific coast of Tohoku earthquake［J］.Earth，Planets and Space，2011，63（7）：785-789.

［10］ YAMADA M，MORI J，OHMI S.Temporal changes of subsurface velocities during strong shaking as seen from seismic interferometry［J］.Journal of Geophysical Research：Solid Earth，2010，115（B3）：B03302.

［11］ SCHERBAUM F.Seismic imaging of the site response using microearthquake recordings.Part Ⅱ.application to the Swabian Jura，southwest Germany，seismic network［J］.Bulletin of the Seismological Society of America，1987，77（6）：1924-1944.

［12］ 王苏阳.基于日本KiK-net地震动数据的场地反应研究［D］.哈尔滨：中国地震局工程力学研究所，2017.

WANG Suyang.Study on site effect using ground motion data from KiK-net in Japan［D］.Harbin：Institute of Engineering Mechanics，CEA，2017.

［13］ NOGUCHI S，SASATANI T.Quantification of degree of nonlinear site response［C］// Proceedings of the 14th World Conference on Earthquake Engineering.Beijing：Seismological Press，2008.

［14］ REGNIER J，CADET H，BONILLA L F，et al.Assessing nonlinear behavior of soils in seismic site response：statistical analysis on KiK-net strong-motion data［J］.Bulletin of the Seismological Society of America，2013，103（3）：1750-1770.

［15］ WU C Q，PENG Z G.Temporal changes of site response during the 2011 MW9.0 off the Pacific coast of Tohoku earthquake［J］.Earth，Planets and Space，2011，63（7）：791-795.

［16］ SAWAZAKI K，SATO H，NAKAHARA H，et al.Time-lapse changes of seismic velocity in the shallow ground caused by strong ground motion shock of the 2000 western-Tottori earthquake，Japan，as revealed from coda deconvolution analysis［J］.Bulletin of the Seismological Society of America，2009，99（1）：352-366.

［17］ WU C Q，PENG Z G，BEN-ZION Y.Refined thresholds for non-linear ground motion and temporal changes of site response associated with medium-size earthquakes［J］.Geophysical Journal International，2010，182（3）：1567-1576.

［18］ FEDERICO D，BONILLA L F，FOTI S.In-situ shear modulus reduction computation using seismic interferometry by deconvolution from borehole and surface data：theory and examples［C］//Proceedings of the 5th IASPEI/IAEE International Symposium：Effects of Surface Geology in Seismic Motion.Taiwan：［s.n.］，2016：15-17.

［19］ BONILLA L F，GUGUEN P，BEN-ZION Y.Monitoring coseismic temporal changes of shallow material during strong ground motion with interferometry and autocorrelation［J］.Bulletin of the Seismological Society of America，2019，109（1）：187-198.

［20］ 張喆，许力生.2021年2月13日日本本州东海岸MW7.2地震矩心矩张量解［J］.地震学报，2021，43（2）：255-259.

ZHANG Zhe，XU Lisheng.The centroid moment tensor solution of the 13 February 2021 MW7.2 earthquake in the east coast of Honshu，Japan［J］.Acta Seismologica Sinica，2021，43（2）：255-259.

［21］ GARDNER G H F，GARDNER L W，GREGORY A R.Formation velocity and density：the diagnostic basics for stratigraphic traps［J］.Geophysics，1974，39（6）：770-780.

［22］ NIED.NIED K-NET，KiK-net，National Research Institute for Earth Science and Disaster Resilience［Z］.2019.doi：10.17598/NIED.0004.