7E教学模式助数学核心素养落地生花

张茹苑 苏克义

【摘要】本文以7E教学模式为主线，借助时效性材料，以“数学之美”的角度引入课题，融函数奇偶性的历史、动手操作法及数学核心素养于教学过程，实现7E教学模式助数学核心素养落地生花.

【关键词】7E教学模式；函数的奇偶性；核心素养

1 7E教学模式

《普通高中数学课程标准》（2017年版2020年修订）中提出数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析六个数学学科核心素养.它们既是数学课程目标的集中体现，又在教学过程中起到关键作用. 因此，教师在进行教学设计时，应该依据课程标准，培养核心素养，体现育人价值.

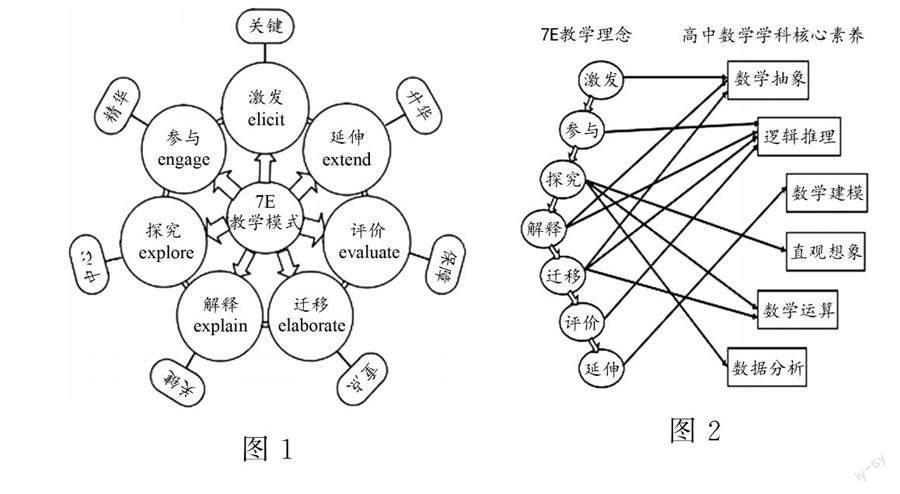
Arthur Eienkraft认为，一个好的教学模式应该与时俱进，他将高度成功的5E教学模式进行扩展，由elicit（激发）、engage（参与）、explore（探究）、explain（解释）、elaborate（迁移）、evaluate（评价）、extend（延伸）组成的7E教学模式应运而生，如图1、图2所示，它们相辅相成，环环相扣，在教学中各司其职，也可随具体情境灵活运用.陈金玲分别针对初中生物教学中运用7E教学模式的具体步骤和相关效果做出详细探究. 本文将其与数学核心素养结合，用7E 教学模式助数学核心素养落地生花.

2 教材分析

本节课选自《人教A版普通高中数学必修第一册》（2019年版）教科书第三章的第二节：函数的基本性质（第二课时），是一节概念课. 在学生掌握函数概念、表示法以及函数图象绘制的前提下，继续探究函数的性质.

在研究方法层面，以坐标系为桥梁，将代数与几何问题相互转化，借助图象探索函数性质，体现了数形结合的思想；在内容结构层面，它既是函数概念的拓展，又是研究基本初等函数的有效手段，具有承上启下的作用；在教学意义层面，有助于发展学生的数学抽象、数学运算、邏辑推理等数学核心素养，培养学生用数学的眼光看待问题，树立正确的价值观.

3 教学过程

3.1 激发［时效案例引入，激发学生兴趣］

教师引导 有人提出奇偶性是函数最美的性质，那么“美”在何处呢？

创设情境 2023年8月25日，谷神星一号遥八运载火箭在我国酒泉卫星发射中心成功发射升空，发射任务获得圆满成功. 作为当代中国青年，同学们定会为祖国的强盛感到自豪，一种震撼之美也油然而生. 这种美体现在形的对称，如图3所示.

设计意图 结合时事材料引入教学内容，吸引学生的兴趣，激发爱国之情. 以“数学之美”为起点探究函数奇偶性，颇具新意，体现了数学抽象素养.

3.2 参与［分享课前成果，引导学生参与］

课程活动 在课前搜集资料的基础上，挑战1分钟讲述函数奇偶性的“前世故事”.

教学处理 邀请三名同学进行挑战，教师对发言进行补充和形成性评价，课后继续该活动，评选本次“故事王”.

设计意图 汪晓勤主张，“知其所以然”才能更好地“知其然”，据此培养学生逻辑推理的素养.牛伟强［6］也认为在回顾历史概念的基础上，设计“函数奇偶性”的教学更有意义.

3.3 探究［设置问题情境，组织开展探究］

请完成以下活动，独立思考后小组合作探究.

探究活动 观察图4、图5，描述这组图片的共同特征.

教学处理 请一组学生分享成果，其他同学补充，正如大家发现：图中均为轴对称图形. 师生回顾轴对称图形特点.

教师引导 事实上，图形的对称性与函数的奇偶性密不可分，如图6所示，下面请拿出课前分发的函数f（x）=x2的图象.

课程活动 已知点L0，2，M0，4，N0，9，现在请按照要求动手操作：首先分别过L、M、N三点作y轴垂线，与图象交点依次记为点A，B，C，D，E，F，观察图象沿y轴折叠是否重合，并记录重合的三组点坐标，最后得出这三组点横纵坐标的关系.

教学处理 得到该函数图象是轴对称图形，其中点A与点F、点B与点E、点C与点D分别重合. 每组对应点的横坐标互为相反数，纵坐标相等.

教师引导 由活动得知：x取±1，±2，±3时函数值分别对应相等. 猜想：对于这类函数，当x取相反数时，y值都相等.

教学处理 教师用几何画板软件绘制函数f（x）=x2图象，任取一点A，过点A作y轴垂线，与函数图象交于另一点B，接着教师平行移动直线AB，得出当横坐标互为相反数时，纵坐标相等，这与刚才的猜想不谋而合.

设计意图 孟俊强调课堂教学应与信息技术融合，教师操作几何画板软件，引导学生自主探究得出结论，培养其数学运算、数据分析素养. 同时，应用“数形结合”思想，为得出偶函数的概念和几何意义做准备.

3.4 解释［引入相应定义，明确几何意义］

教师引导 如何用数学语言描述以上类型的函数呢？

教学处理 得到偶函数定义和几何意义. 同理，可类比学习奇函数的定义及几何意义.

设计意图 黄继蓉等认为数形结合思想应贯穿于数学教学的始终，因此教师通过启发性问题引导学生由“形”过渡到“数”再抽象出“定义”和“几何意义”，该过程能够培养学生数学抽象、逻辑推理素养.

3.5 迁移［应用所学新知，补充相关理论］

牛刀小试1 绘制图象判断下列函数g（x）=x2+110x4的奇偶性，再用定义验证结论.

设计意图 先后应用函数奇偶性的几何意义和定义进行针对性训练，如图7，得出图象法判断函数奇偶性的流程.

牛刀小试2 根据定义判断函数f（x）=1x5+x11， x∈（－1，2）的奇偶性.

设计意图 本题是牛刀小试1的进阶题目，精心设计，意在强调首先要判断定义域是否关于原点对称，如图8，最后得出定义法判断函数奇偶性的流程.

牛刀小试3 已知fx是x>0上的奇函数，当f（x）=－2x2+3x+1时，求fx的解析式.

设计意图 利用奇偶性定义确定函数表达式，是对新知的进一步应用，可以培养数学抽象、逻辑推理、数学运算素养，提高学生应用能力.

教师引导 对于判断函数奇偶性，除定义法、图象法外还有其他常用方法吗？

教学处理 如表1所示，引入复合法判断函数奇偶性.

设计意图 教师应引导学生发散思维，及时补充知识，使教学内容更加完整，以此培养学生逻辑推理素养.

3.6 评价［多种评价结合，总结教学优劣］

教学处理 对于学生，采用“自评、生生互评、教师评价”三级评价体系，并在课后进行小测验，以保证学生清楚掌握自己的学习情况. 对于教师，采用“自评、学生评价、其他教师评价”三级评价体系，以便及时了解学生学习状况、教学效果等.

设计意图 评价环节既要求学生对学习情况有清晰认知，又需要教师对教学过程进行反思.以此达到更好的教学效果，体现了数学教学的逻辑性.

3.7 延伸［延伸课堂思维，理论联系实际］

教學处理 思考如何将所学的函数奇偶性的知识应用到生活实际中？如何与其他学科内容结合？

设计意图 “举一反三者，博学.” 新课改下的教学观要求教师由“教会学生知识”转变为“教会学生学习”，因此教师应抛砖引玉，引导学生举一反三，应用所学知识解决现实问题和其它学科问题.

4 结语

本节课借助高效的7E教学模式，通过时事政治，结合函数奇偶性的历史，以“数学之美”的角度引入教学，引导学生动手操作、自主探究. 主要内容为函数奇偶性的定义和几何意义，并会根据定义法、图象法、复合法判断函数奇偶性，了解函数按照奇偶性的四种分类. 在此过程中，调动学生积极性，培养数形结合、应用新知和以数学的眼光看待问题的能力，增强六大数学核心素养，实现7E教学模式助数学核心素养落地生花.

【本文系宁夏大学研究生教育改革创新与实践项目（项目编号：JXAL202205）研究成果】

参考文献：

［1］中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［S］.北京：人民教育出版社，2020.

［2］Expanding the 5E Model： A proposed 7E model emphasizes “ transfer of learning ” and the importance of eliciting prior understanding［J］. The Science Teacher，2003，70 （6）.

［3］陈金玲.“7E”教学模式在初中生物教学中的实践研究［J］.教师，2020（16）：81-82.

［4］马岩.基于7E教学模式提高初中生科学探究能力的实践研究［D］.上海：华东师范大学，2021.

［5］汪晓勤.“奇、偶函数”考源［J］.数学通报，2014，53（03）：1-4.

［6］牛伟强.数学史视角下的探究性学习——“函数的奇偶性”教学设计与思考［J］.教育研究与评论（课堂观察），2016（05）：44-47.

［7］孟俊.信息技术与数学教学融合的实践探究——以“函数奇偶性”教学为例［J］.中学数学教学参考，2022，No.863（21）：12-14.

［8］黄继蓉，陈光喜，黄文韬.多媒体技术与数学“数形结合”教学［J］.数学教育学报，2009，18（02）：76-78.