基于多类型信号多平台的无人机定位方法*

袁 江 兰增武 熊 鹏

（中国长江电力股份有限公司 宜昌 443000）

1 引言

随着社会的发展，国家的大型工程对安全和保密的要求也越来越高。因此，大型工程反无人机的需求非常旺盛，许多重点工程也已加装了反无人机系统。无人机的入侵有多种形式，有单无人机入侵，有多无人机入侵，有白天入侵，也有夜晚入侵。每种形式，都对反无人机系统的无人机探测部分提出了不同的要求。例如多无人机入侵就会有定位出现虚假点的问题，夜间入侵时监视摄像头会不起作用的问题。因为要求不一样，因此目前的无人机检测技术，所适应的场景的广度一直都不够。

本文基于红外线辅助功能的无人机摄像头探测单元作为前端传感器，建立多径回波信号的目标检测模型，最后使用多平台无源定位法，动态与静态相结合的方式，给出入侵无人机的实时坐标。结合多种探测方法，加上对无源定位算法的改进，可以提高无人机检测的适应场景广度。

2 多角度摄像头探测

整个检测系统的前端使用一种基于红外线辅助功能的无人机摄像头探测单元。探测单元包括发射红光的红光灯、能够透过红光的滤光片，以及探测孔。其中，所述滤光片位于探测孔。一般人眼可以感知到电磁波长在400nm～760nm 之间，红光波长范围是760nm～622nm，上述滤光片采用600nm的长波通滤光片，能够透过红光。人眼感受不到红外线，但探测相机的感光原件的感知是在红外线光谱范围之内的，通过上述滤光片，便可查觉到无人机相机发射的红外线的存在。

夜间探测时，摄像头探测单元处于光线不足的暗环境中，由于摄像头探测单元设有用于发射红光的红光灯，如此通过红光灯发射红光，如果远方有无人机，红光照射到无人机摄像头镜面上会发生反射，反射回来的光波长和发射的光波长是相同的。

反射回来的光到达滤光片，由于滤光片能够透过红光，其他颜色的光被滤光片过滤掉，这样滤光片上就会出现一个红点。从而实现对具有红外线辅助功能的侦测无人机的探测。在探测到无人机的同时，摄像头探测单元还可以通过发射光线的方向判断出无人机所处的方向。图1 为摄像头探测单元结构图。

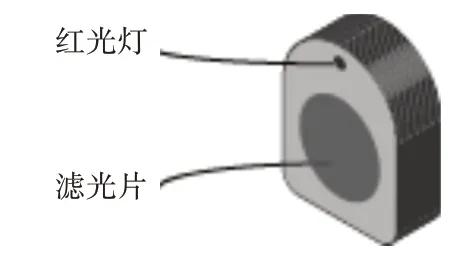
图1 摄像头探测单元结构图

图1 的摄像头探测单元结构简单成本低，但有探测角度小的问题。且飞行的无人机在侦测的时处于运动状态中，其摄像头的角度是不固定的。这样会使摄像头探测单元探测到无人机的概率降低，影响实用性。

针对“1”所述的摄像头探测单元在探测角度上局限性，同时又针对摄像头探测单元成本低结构简单的特点，可对其进行优化，使其能扩大探测范围和探测角度，从而提高探测概率。

如图2 所示，将多个摄像头探测单元按不同角度安装，角度可以是三维空间内的角度。进一步地，给每个摄像头探测单元加装旋转云台，机械臂等可以改变方向的装置，形成一个多角度摄像头探测模块。多角度摄像头探测模块可以有效地扩展探测出无人机的角度。

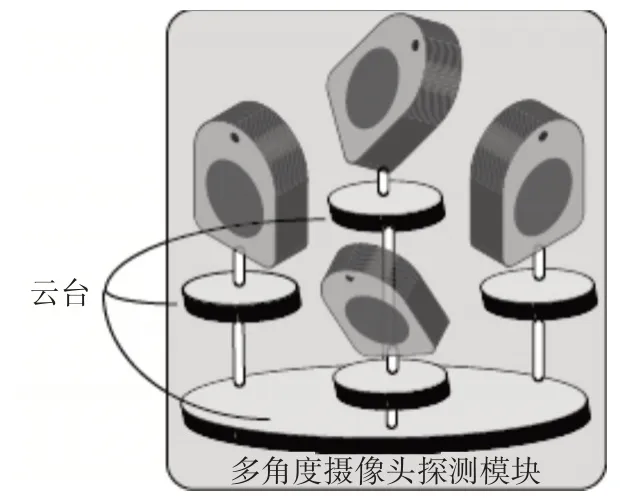
图2 多角度摄像头探测模块结构（探测平台）

3 目标检测模型

3.1 低空多径传播

无人机在飞行时传递的信号，除声音外，都可以归类于电磁波范畴中。而电磁波的传输过程会随着其所处空间物理特性的不同产生传播行为和传播模式的改变。在低空飞行的无人机发出的电磁波会受到山脉、峡谷、高楼等各种地形地物的阻碍，而阻碍物不同的几何特性和电磁特性会导致无人机发出的电磁波出现反射、透射和衍射等多种传播行为。其中，对无人机目标检测最有作用的是多径反射。

常见的两种反射模型是理想平面反射模型和近似平面反射模型。其中，理想平面反射模型就很适用于目标的高度较低，距离较近的非合作无人机入侵场合，这种情形下的探测器和目标的高度在米量级，距离在千米量级。理想平面反射模型示意图如图3所示［1］。

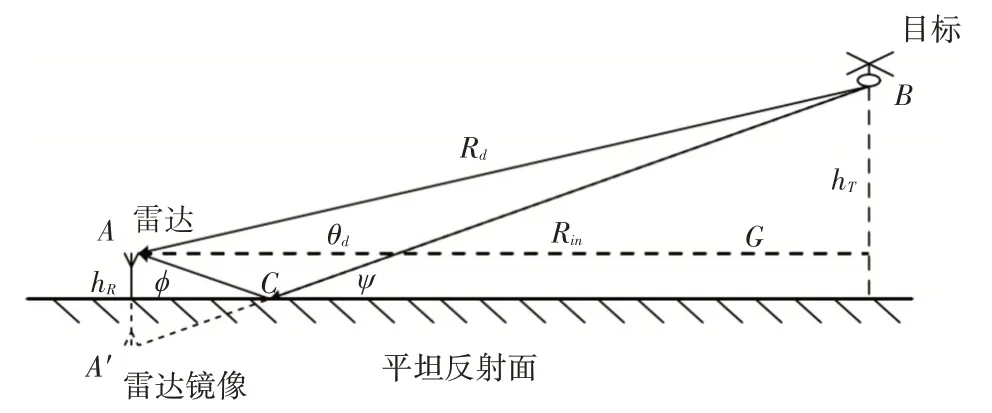
图3 理想平面反射模型

探测雷达位于点A处，高度为hR，无人机目标位于点B处，高度为hT。目标和探测雷达之间的距离为Rd，水平距离为G，一般来说，hR和hT相对于G来说可以忽略不计，因此可以使用近似计算，得到探测雷达信号的直达路径与反射路径的长度分别为

式（1）的两式相减，可得直达路径与多径路径的路程差为

3.2 多径回波信号分析与建模

本文的研究对象是低空小型无人机，符合理想镜面反射模型的“低空”“近距离”的要求。因此，多径信号传播模型可以参考如图3。图3 中，点C为信号从点A出发反射到目标无人机B的反射点，从探测器到点C再到点B的距离为Rin。由于高阶多径回波的能量下降明显，因此仅考虑二阶及以下的多径回波。各阶次多径及其对应的路径长度如表1 所示［1］。

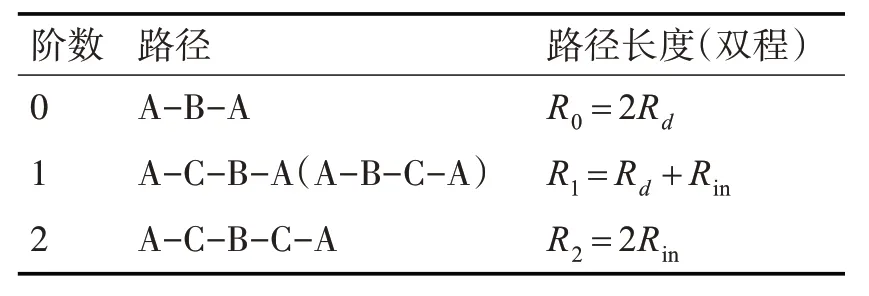
表1 各阶多径传播的路径长度

由表1 可知，存在两条1 阶多径，这两条1 阶多径拥有相同的路线，入射和反射的方向相反，因此这两条1阶多径会产生同样的时延。

相应地，代入不同阶数多径回波的时延τi以及表1 中的不同阶数多径路径的长度，结合上一节给出的多径反射系数的概念，可以分别得到各阶多径回波的信号形式为

直达波：

一阶多径回波：

二阶多径回波：

将式（3）、（4）、（5）相加，即可得到最终接收机接收到的回波信号，即

4 主从多平台无源定位

4.1 多平台定位原理

当空域中出现多个无人机目标时，检测时会产生虚假目标问题。如图4所示［2］，假设有三个平台，则三条角度射线的交叉点有四个，其中真实目标无人机3 个，虚假目标为1 个。 除了虚假目标，多平台的多目标检测还存在比平台数量少1 的波门数量，如图5所示［2］，波门区域重合处可形成更小更精确的波门区域。由现有的理论和实践可得出，重叠的波门区域会随着平台数量的增加而减小。

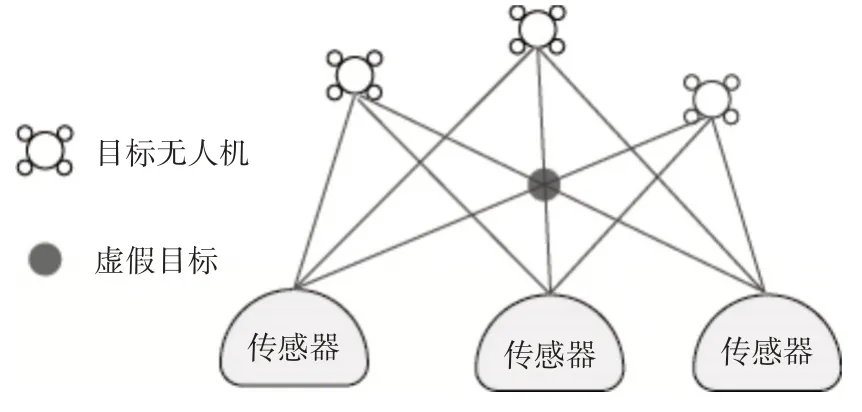
图4 多平台无源交叉定位虚假点示意图

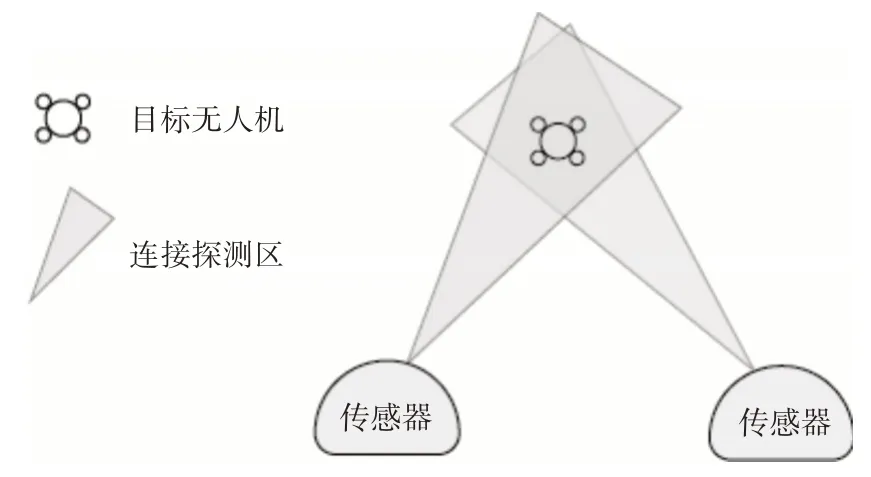
图5 多平台无源交叉定位波门区域示意图

因此，增加平台的数量，交叉点形成的虚假目标会减少，波门区域会变小，波门中的交叉点数量也会减少。所以，增加平台数量可使多目标定位的精度大大提高。但是，平台数量的增加也会使系统的复杂度呈几乎式增长，包括解算复杂度，平台间的数据通信频次，同步难度等等，还推高了系统成本。因此，实际应用中，平台数目不能无限增大，应选择一个高性阶比的择中的平台数目。

本文采用了多平台对多目标融合定位方法，通过融合协调平台数目、平台布局以及虚假点滤除算法，准备识别出真正的无人机并获得较高的定位精度。

例如使用三平台联合空间三角布局，首先，将两个平台放于同一高度，通过方位角的交叉定位［3］可确定目标的水平距离；然后，将第三个平台在垂直面上与前两个平台通过俯仰角的交叉定位［4］确定垂直距离，形成相互约束，用于消除虚假目标；最后，通过解耦的方式进行定性分析，实现对目标无人机精确的三维定位。

多平台多目标定位系统的实现结构图如图6所示［5～8］。

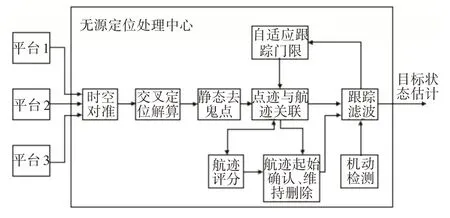
图6 多目标多平台无源定位系统的实现结构

4.2 侧向与时差定位

4.2.1 侧向定位法

测向定位法是利用多个平台获得目标无人机的角度信息，根据平台位置坐标和角度值可以在空间中确定每个经过目标无人机的直线，从而根据直线的交点确定无人机的位置［9］。

假设布置的N个平台坐标矩阵为是Si=(xi，yi，zi)，i=1，2，…，N，其中，平台i测得的方位角为θi，俯仰角为φi，目标无人机的坐标为(x，y，z)，根据空间几何学，方位角和信仰角可由下式求得：

4.2.2 时差定位法

时差定位法是在平台位置坐标己知的情况下，通过对同一目标无人机发出的信号到达不同平台的时差进行处理来对目标无人机进行空间定位。同时根据几何学原理，要实现定位，二维空间中最少需要3个平台，三维空间最少需要4个平台［10～13］。

时差定位法可分为两步：

1）使用时差测量算法，测得目标无人机信号到达多个平台的时间差，通过时间差可以确定出一组关于目标无人机坐标的非线性方程组。

2）使用时差定位算法，从非线性方程组中解得一个最优解。

假设定位系统平台数量为N［14］，位置为si=(xi，yi，zi)T，其中i=0，1，2，…，N。设i=0 表示主平台，i=0，1，2，…，N表示辅平台。目标辐射源的位置为u=(x，y，z)T；设ri表示目标无人机与第i个平台的距离，ri0表示目标无人机到第i个平台与其到主平台之间的距离差，τi0表示目标到第i个平台与到达主平台的到达时间差［9］，则时差法定位法测量目标位置的方程如下：

4.3 主从分布式安装

在实际应用中，在待保护的工程（XX 电站、XX基地等）的关键的地方（中控室，关键结构部位等）都安装上图2 中所述的探测平台，通过局域网络，将探测平台连接起来，形成一个无人机探测子系统。图7 为无人机探测子系统分布式安装示意图［14～16］。

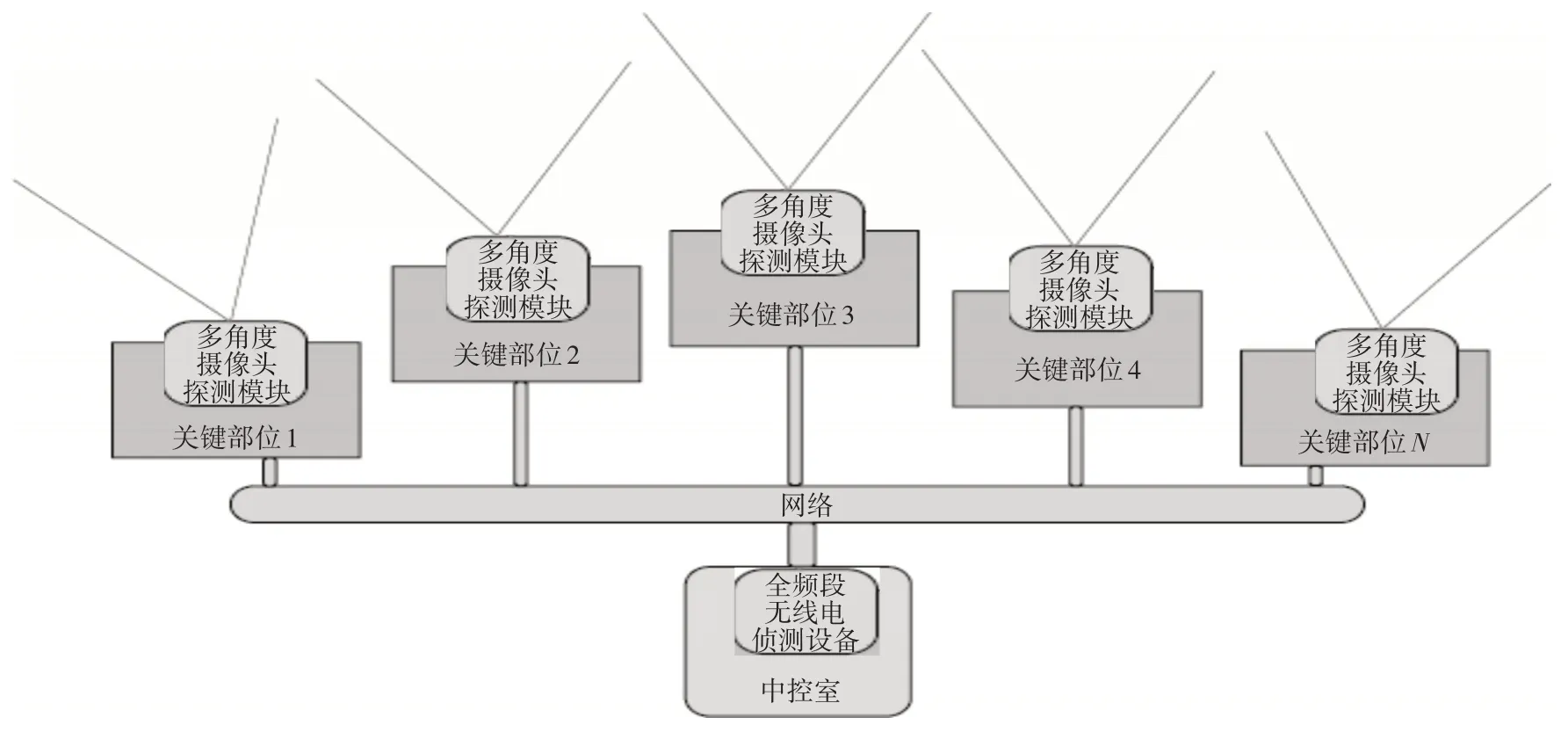
图7 无人机摄像头探测子系统分布式安装示意图

然后，红外探测子系统与其他探测系统（全频段无线电探测系统，光电探测系统，探测器探测系统）一起，形成无人机探测分系统。最后，无人机探测分系统和无人机反制分系统以及无人机防控指挥分系统通过全局网络连接在一起，形成待保护的工程所需的无人机防控系统。图7 为无人机防控系统的结构图。

5 结语

目前，尽管反无人机技术的研究如火如荼，但无人机的飞行技术也在不断进步，这就给反无人机技术提出了更高的要求。因此无论是无人机检测、反制、干扰，都还有很大的上升空间。尤其是在无人机的检测方面，无人机的各类特征都可以用作检测的对象。以后，在无人机检测和定位上还可以进一步研究，以使检测更快速，定位更精确。