基于K-means 与SVR 的致密油藏水平井压裂产能预测研究*

刘新平 邓 杰 杨鹏磊

（中国石油大学（华东）计算机科学与技术学院 青岛 266580）

1 引言

致密油藏是当今非常规油气开采的主要来源之一，随着近年钻井水平和开发技术的进步，多数油田已采用水平井配合体积压裂技术的开采方式来替换原有开发手段而达到增产和提高采收率［1］。在这样的开采模式下，研究致密油水平压裂井长时间持续高产的主要因素以及准确预测油藏产能，对后序致密油的高效开发具有重要指导意义［2］。

自Giger［3］1985 年首次论述压裂水平井的产能问题之后，相继出现了一系列的研究方法，这些方法大致可以分为两类：一类是纵向预测，主要是以非达西渗流［4］为基础推导出的产能公式，另一类是横向预测，主要是用模式识别等数学方法来处理参数，从而建立产能预测模型。以非达西渗流为基础的产能公式又可根据不同的油气田开发阶段、不同方法的适应性将产能评价方法分为解析法和数值模拟法［5］。解析法主要假设地层为均质、流体为单相渗流，对于早期开发井的部署具有一定的实际意义；数值模拟法在20世纪90年代才逐渐成熟，可以在精细油气藏模型构建的基础上，利用基础的渗流理论对复杂的对象进行仿真模拟，但是该方法需要丰富的储层、流体、动态的资料作为支撑才能达到好的应用效果。解析法和数值模拟法都有其特定的适用范围，由于影响致密油产能的因素可为地层因素、原油物性因素、压裂施工因素，而每一项因素中又存在多种子因素，且相关子因素又存在某种相关性，其中地层因素与原油物性因素又因不同区域存在较大差异，不能适用于多种地层，对每一口井的不同层位进行解释时都需要选择不同的经验公式，极大地增加了预测的难度和准确性。

机器学习和深度学习［6］技术具有极强的数据挖掘能力，主要通过模式识别等数学方法来处理参数，从而建立产能预测模型。目前国内外学者已经开始应用机器学习方法进行产能预测和压裂参数优化，LUO 等［7］利用井深、射孔厚度、孔隙度、含水饱和度、压裂段数、压裂液用量和支撑剂用量来建立神经网络模型，得到第一年采油量与重要特征之间的关系；宛利红［8］利用四种测井参数对致密油产能进行分析，建立了上述四种测井参数与采油指数的关系模型；王威［9］采用灰色关联度分析法、复相关系数法和熵值法，分析了体积压裂后初期产能与影响因素的相关程度，得到支撑剂用量，压裂液用量，渗透率和地层压力为重要影响参数；周于皓［10］基于循环神经网络对缝洞型油藏的单井产能进行预测，学习到了油井产量的变化规律；WANG 等［11］对加拿大的Montney 储层的3610 口压裂水平井进行了分析，应用人工神经网络、支持向量机等多种机器学习算法进行了预测评估。由于实际油田现场是以区域来划分，各区域参数不一，单一模型的使用不完全满足所有区域特征。

本文提出基于K-means 聚类分析与支持向量回归的组合预测模型，通过主成分分析方法计算筛选后的地质类和原油物性类因素权重系数，对其特征进行赋权再聚类从而解决K-means 中欧式距离对所有特征贡献程度一致的缺点［12］；K-means聚类结果来代表地质类参数和原油物性类参数对产能的影响程度，聚类结果与压裂类参数结合作为SVR［13～14］预测的训练样本［15］。通过实验对比了相同数据下BP神经网络模型，SVR 模型的表现情况，其结果表明，本文提出的组合模型具有较优的准确性和合理性，组合模型中先聚类的方式解决了不同区域地质与原油物性的差异影响，故提高了模型的精度从而满足油田现场精度要求。

2 油藏数据预处理

影响致密油水平井压裂后产能的因素较多，总体分为三个类别：地质类特征、流体物性类特征、压裂施工类特征。主要包括：地层密度、地层粘度、凝固点、含蜡、胶质、饱和压力、溶解气油比、总矿化度、渗透率、孔隙度、自然伽马、段数、簇数、压裂液用量、支撑剂用量等。

2.1 数据标准化

各种参数的度量单位不同，如：原油粘度（mPa·S），渗透率（mD）。为了便于不同单位或量级的指标能够进行比较和加权，将数据统一变换为无单位（统一单位）的数据集，采用最大-最小标准化方法消除量：

式（1）中：x为数据清洗后的样本数据，xmin，xmax为样本数据中各参数的最大值和最小值，x*表示归一化后的样本数据。

2.2 主控因素提取

过多的参数会提高模型的复杂程度，可能导致过拟合，影响程度较小的参数会降低模型的准确率，故对各类参数进行主控因素分析，按照相关性排序来筛选。本文采用灰色关联分析方法来计算各个参数与产能的相关性。

通过灰度关联分析算法，可得到特征值（子序列）与周期（母序列）关联度大小的排序，关联度越高则表示两个因素变化的趋势具有强一致性，即同步变化程度越高。子序列的各个指标与母序列的关联系数计算方法如下：

式（2）中ρ为分辨系数，0 ＜ρ＜1，若ρ越小，关联系数间差异越大，区分能力越强，通常ρ取0.5；x0(k)和xi(k)分别表示母序列第k个数和子序列第i个特征值的第k个数；ζi(k)则表示第i个特征的第k个值与母序列第k个值的关联系数。通过关联系数来计算关联度再进行最后的排序。其中关联度得计算如下：

式（3）中ri为第i个特征与母序列的关联度大小，n为样本数量。基于计算结果，对所有ri进行排序即可得到关联度排序。最终选取参数为

1）地质类参数：渗透率、孔隙度、声波时差AL、自然电位GR、自然伽马SP；

2）原油物性类参数：原油粘度、原油密度、含有饱和度、溶解气油比、总矿化度；

3）压裂施工类参数：支撑剂用量、压裂液用量、段数、簇数、返排率；

最终选取以上15 个特征作为算法模型的数据集。

2.3 特征赋权

权重系数的大小与影响目标的重要程度有关，传统K-means 聚类算法通过欧氏距离计算样本的相似度，将数据所有的属性特征均平等的对待，忽略每个特征的不同贡献，导致样本相似度计算的准确率不高。本文采用主成分分析算法计算地质类与原油物性类特征权重系数并赋值解决K-means中欧氏距离的硬聚类问题。表1 为通过主成分分析计算权重后地质类与原油物性类特征的权重系数，对赋权后的特征再生成新的样本数据。

3 致密油产能预测模型建立

由于地质类参数与原油物性类参数属于静态参数，即同一区域油藏的地质和物性参数基本一致，故采用K-means聚类算法对赋权后的地质类与原油物性类样本进行分类，得到的无监督分类结果代表影响程度再与压裂施工参数结合作为SVR 的训练数据，构建产能预测模型。

3.1 K-means聚类原理

利用K-means算法在样本集上对静态参数（地质类参数、原油物性类参数）进行分类，以聚类结果代表不同区块静态数据对产能的影响程度。具体K-means算法步骤如下：

算法1 特征赋权后的K-means聚类算法

1）初始化，确定聚类数目K和初始化聚类中心；

2）计算各样本特征赋权后距K个初始中心的距离，按照距离大小将样本分配给最近的中心点，形成K个聚类。

式中Zik为样本点，r为参数的权重系数，Zjk为聚类中心点。

3）计算每一类的均值，并以此为K个聚类新的聚类中心。

式中：Ci为样本集和，mi为聚类中心，Zq为样本。

5）重复步骤2），3）至E摆动很小，聚类结束，得到聚类结果。

3.2 支持向量回归实现原理

基于SVR 的预测模型函数为F(x)=wϕ(x)+b，式中：w为权值向量，ϕ(x)为聚类后的结果与地质类参数结合的新样本，b为偏置向量。由于SVR 存在容忍偏差ε，于是SVR问题可形式化为

式（4）中C为正则化常数，Loss为损失函数：

为了确保大部分数据参与模型训练，引入松弛变量ζi和ζi*，则优化为

由拉格朗日乘子法可得拉格朗日函数：

在KKT条件下，拉格朗日的对偶形式为

将其对偶形式求解获得回归函数为

式（9）中K(xi，xj)=ϕ(xi)Tϕ(xj)为核函数。在SVR 产能预测模型中，核函数K（x，x）的类型对模型的性能影响较大，可以通过比较不同核函数的性能情况来选择最佳核函数类型。

3.3 致密油产能预测组合模型构建流程图

应用单一模型在多因素影响下往往预测效果不够理想，且地质类参数与流体物性类参数属于静态参数，为准确预测产能，本文将结合K-means 与SVR两种机器学习模型，以充分发挥组合模型的优势，构建流程如图1所示。

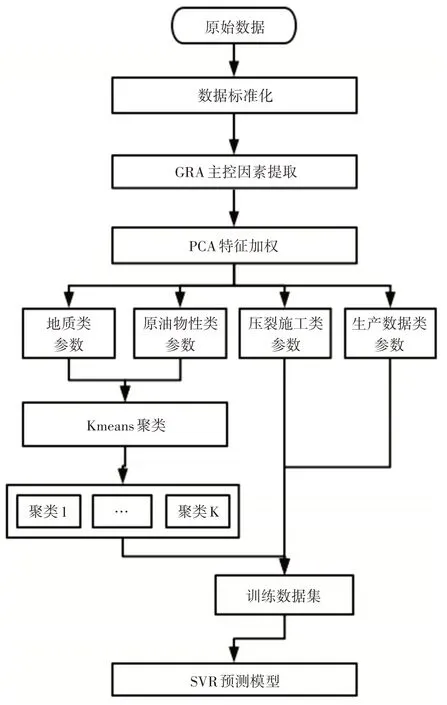
图1 组合模型构建流程图

4 实验结果对比

为了进一步验证本文提出的基于K-means+SVR组合预测模型的准确性和可靠性，将该组合模型与单一模型SVR、BP 神经网络模型进行预测对比。通过网格搜索算法寻找到SVR 模型最优参数C=1.17，g=1.8；基于K-means+SVR组合模型的部分预测结果如图2所示，样本拟合情况较好。

图2 K-means+SVR预测结果部分展示

通过图3 三种算法在测试集中部分井的预测结果与实际投产当年累计产油量的对比结果可以看出：K-means+SVR 组合模型的产能预测效果更贴合真实值，拟合效果更优。

图3 算法预测结果对比图

表2 为三种预测模型在均方误差（Mean Squared Error，MSE）和平均绝对误差（Mean Absolute Error，MAE）下的评估指标情况，其计算公式为

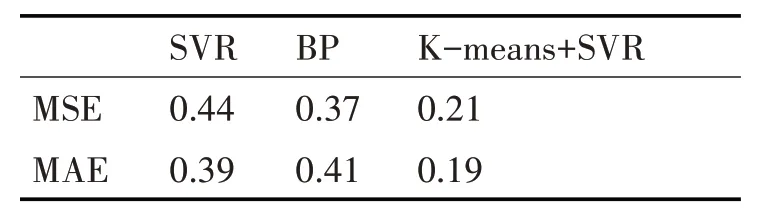
表2 预测模型评价指标

其中m为数据量，h(xi)和yi分别为预测值和真实值。

5 结语

本文针对致密油藏情况复杂的一系列问题，通过主成分分析算法（PCA）计算各特征权重并赋值，从而解决了K-means中欧式距离的硬聚类问题；采用K-means聚类算法对数据样本中静态数据（地质类数据和流体物性类数据）以聚类结果代表不同区域影响程度，解决了不同区域间地质差异性问题，简化了决策参数的数据类型，最终通过聚类结果和压裂施工类参数结合后的样本进行SVR 预测分析。采用本文方法的组合模型，避免了单一预测模型泛化能力差，预测精度不足等问题，通过实验结果验证其预测效果比常规SVR，BP 神经网络模型更贴合实际产能，更能满足现场施工的精度要求，且通过聚类的结果可以对不同区域的最优产能井的压裂施工参数进行研究，从而对新井压裂工艺设计的方案编制具有指导和借鉴意义。