基于PSO-SVM 的制造业采购经理指数预测*

汪 明 李少波 傅 广 马 旺

（1.贵州大学机械工程学院 贵阳 550000）

（2.贵州大学公共大数据国家重点实验室 贵阳 550000）

1 引言

采购经理指数（PMI）最早起源于20 世纪30 年代，它是通过对采购经理或者企业采购的主要负责人的月度问卷调查结果汇总计算得到的。国家统计局以及相关的机构每个月都会进行调查并且公布在国家统计局的网站上。中国PMI 指标体系和国际上主要国家PMI 体系基本相同［1］。作为国际上惯用的监测宏观经济的先行性指标之一，PMI具有很强的预测性，涉及《国民经济行业分类》（GB/T4754-2017）中制造业的31个行业大类，3000家调查样本。它几乎涵盖了企业生产、运输、采购、雇员、配送等企业运转的每一个流程，可以衡量一个国家的生产情况，就业情况以及物价表现。是反映经济增长与衰退的晴雨表［2］。同时对于政府来说，通过采购经济指数也便于为监督和决策工作提供依据［3～4］。采购经理指数一般分为制造业采购经理指数、非制造业采购经理指数以及综合采购经理指数。采购经理指数以50%作为国家经济形势的分界线（荣枯线），PMI＞50%表示经济总体扩张，多数企业愿意生产，企业营收可观，此时企业可扩大生产规模，新建生产线，招聘更多的员工，经济总体趋势向好。PMI＜50%表示经济总体收缩，多数企业不想生产，生产和销售不成正比，库存积压严重，企业可能面临裁员的风险，经济在衰退。对于大多数的中小生产企业而言，PMI主要可以反映各企业目前的营运状况，可以为企业的生产经营提供依据，更能有助于企业管理层预测行业未来的经济的趋势。在如今高速发展的社会，企业如果能更快地掌握行业经济形式，就能减少“牛鞭效应”，提前布局，提前规划［5］。更合理地安排企业生产运行的各个环节，提升企业的整体竞争性。而企业新建生产线扩大产能需要的时间较长，所以根据历史的PMI值预测未来的PMI 值对于企业来说尤为重要。对于PMI 的预测可以为企业规划布局提供理论依据及参考。本文通过PSO-SVM 算法对PMI 进行了预测，并且对比了PSO-SVM 算法与传统SVM 算法的预测准确性。

2 PSO-SVM算法

2.1 支持向量机（SVM）

支持向量机的非线性回归问题就是拟合一条曲线y=f(x)，使训练的样本基本拟合在一条曲线上。它是依靠一个非线性映射将数据映射到一个高维空间，再到高维空间进行线性回归［6］。在本文中假设有一组训练样本信号集(xi，yi)，i=1，2，…，N，其xi∈Rn，yi∈Rn，N为样本的数量。通过一个映射函数Φ(x)实现从低维空间到高维空间的非线性映射。函数f(x)转换为如下形式［7］：

式中，y为输出向量；x为输入向量；W为权重系数；b为偏置项；Φ(x)为输入向量在高维空间上的映射函数。

因为预测值和实际值之间会有偏差，所以引入不敏感损失函数ε：

式中，f(x，w)为SVM 的预测值；y为样本集的真实值；w为权重参数。

假设在支持向量机回归学习的精度ε下，所有样本表示为

函数的回归最优化问题等价于如下函数最小化问题：

在SVM 训练学习中，非线性拟合曲线会存在一定的偏差，为了适应这种偏差，需要添加一个松弛变量ξi［8］。如图1所示，松弛变量添加后拟合曲线更加精确。此外，还需要引入惩罚系数C，并且在引入一个惩罚系数C后，此时函数的回归最优化问题变为

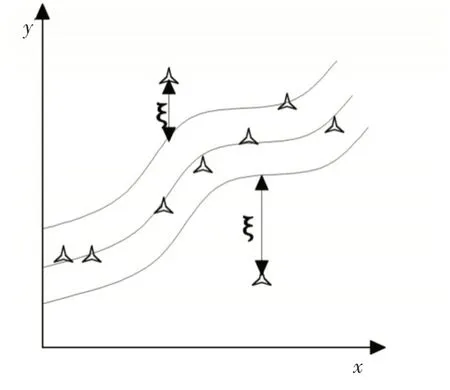
图1 SVM非线性拟合曲线

惩罚系数C对支持向量机的预测准确率有较大的影响，所以惩罚系数C的选取尤为重要。

为了求解最优化问题，在引入拉格朗日乘子对偶参数αi、和径向核函数k(xi，xj)后，式（5）这个具有线性不等式约束的二次规划最优问题可以转化为如下问题［9］。

由于高斯径向基（RBF）核函数计算量小，运算快，收敛区间宽，适用于小样本的数据处理。所以本文采用RBF核函数，RBF核函数如下所示［10］：

式中σ为核参数，对支持向量机的预测准确率也有较大影响，通常选取的C和σ不能确保支持向量机预测的准确率，所以我们引用粒子群算法对参数C和σ进行寻优。引入核函数后求解最优回归函数表达式为

2.2 粒子群算法

粒子群优化（Particle Swarm Optimization，PSO）算法是Kennedy 和Eberhart 在1995 年提出的一种群智能优化算法［11］。粒子群算法是受鸟类在觅食的过程中个体和整体行为规则的启发，在PSO算法中个体最优值是个体经过的最佳位置，全局最优值是种群觅食过程中的最佳位置。在不断的迭代过程中，每个粒子会根据个体最优值和全局最优值更新自己的速度和位置［12］。算法经过随机初始化后，每个粒子按如下式（9）和式（10）进行迭代，直到满足收敛准则：

式中，为粒子i在上一次迭代结束后的速度且，在迭代过程中如果粒子的速度超过了vmax，则认为粒子的最大速度为vmax；表示粒子i在任意t+1 时刻的速度和位置的更新；为粒子在i时刻的位置；w为惯性权重；c1为认知参数；c2为社会参数；为个体i在迭代过程中的历史最优位置；gbestt为迭代过程中所有粒子的全局最优位置。粒子群优化算法流程如图2 所示，通过不断迭代更新个体最优位置和种群最优位置来满足迭代条件。

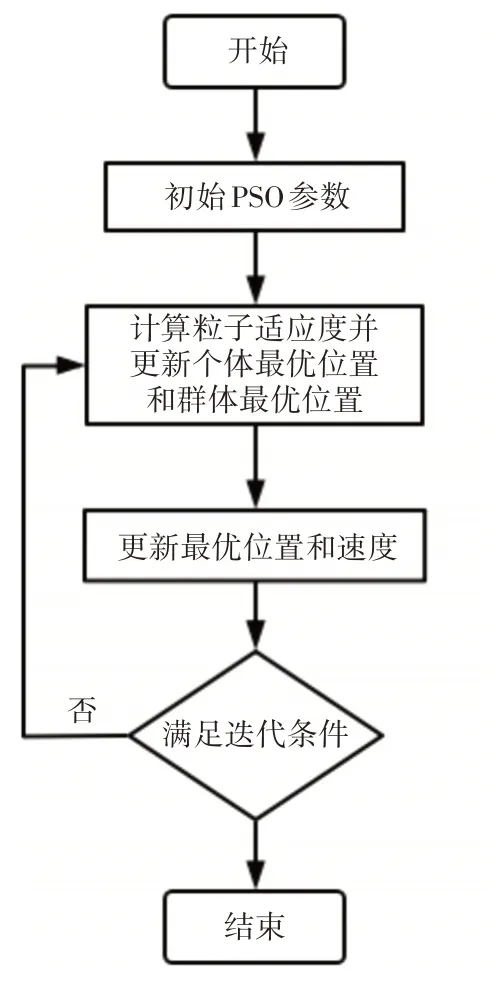
图2 粒子群优化算法流程

2.3 粒子群算法优化支持向量机

用粒子群算法优化SVM，实际上就是优化参数惩罚系数C和核参数σ［13～15］，其寻优过程如下：

1）生成训练的样本，进行归一化处理到［0，1］区间，并划分数据集。

2）初始化参数C1、C2以及最大进化数量、种群最大数量等参数。

3）通过更新粒子的速度、位置等参数寻优SVM。

4）利用最新得到最优惩罚参数C与核参数σ重新训练一次支持向量机。

5）用训练的PSOSVM对数据进行预测。

3 实验与结果分析

本文用Matlab2019 进行实验仿真，对比PSOSVM 与SVM 的预测准确率。采取的实验数据来自于国家统计局［16］。本实验选取了从2016年12月到2021 年3 月的月度制造业采购经理指数，共计52个实验数据，分成13 组。用前四个月的制造业采购经理指数预测后四个月的采购经理指数，原始数据如表1所示，归一化处理后的数据如表2所示。

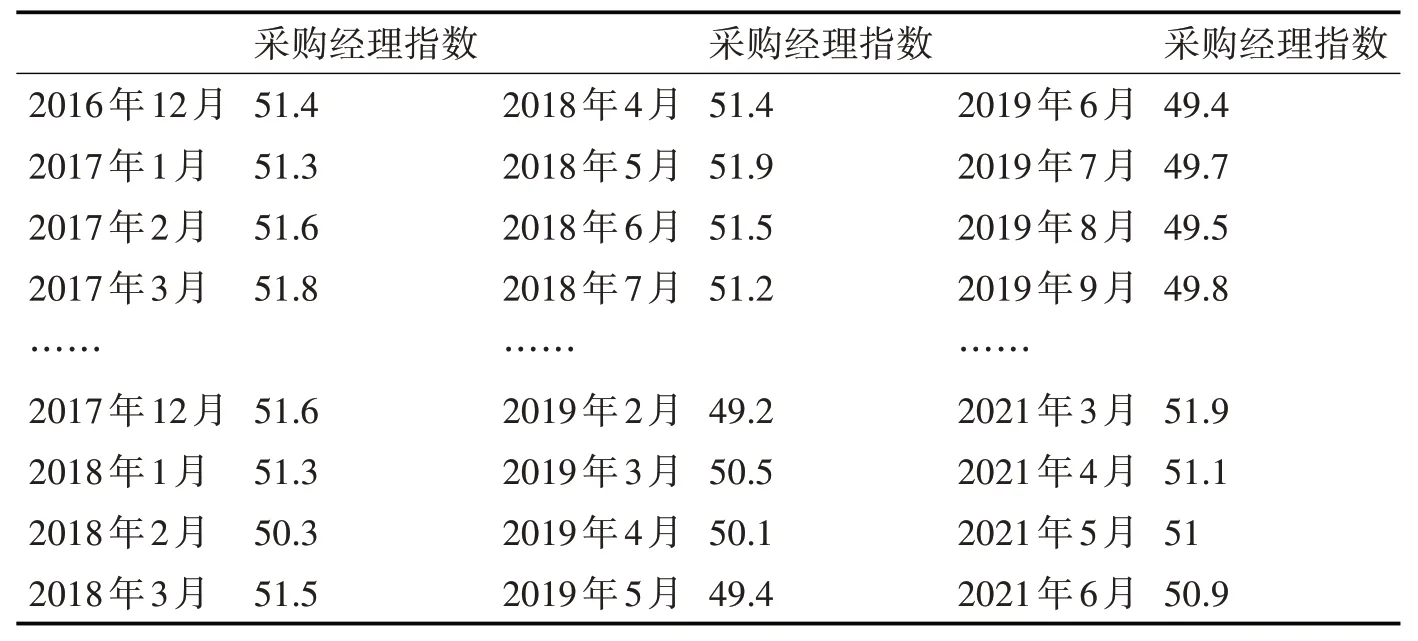
表1 原始数据

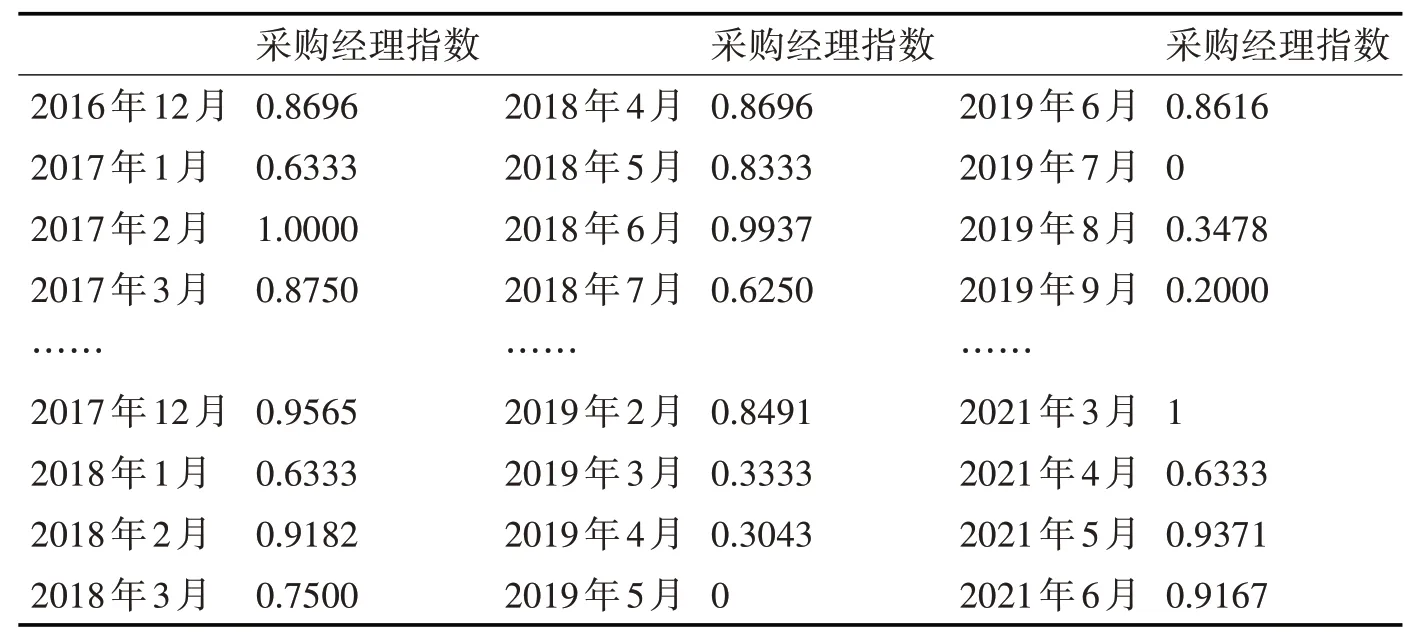
表2 归一化处理后的数据

在只运用传统支持向量机的情况下用Matlab进行仿真结果如图3。

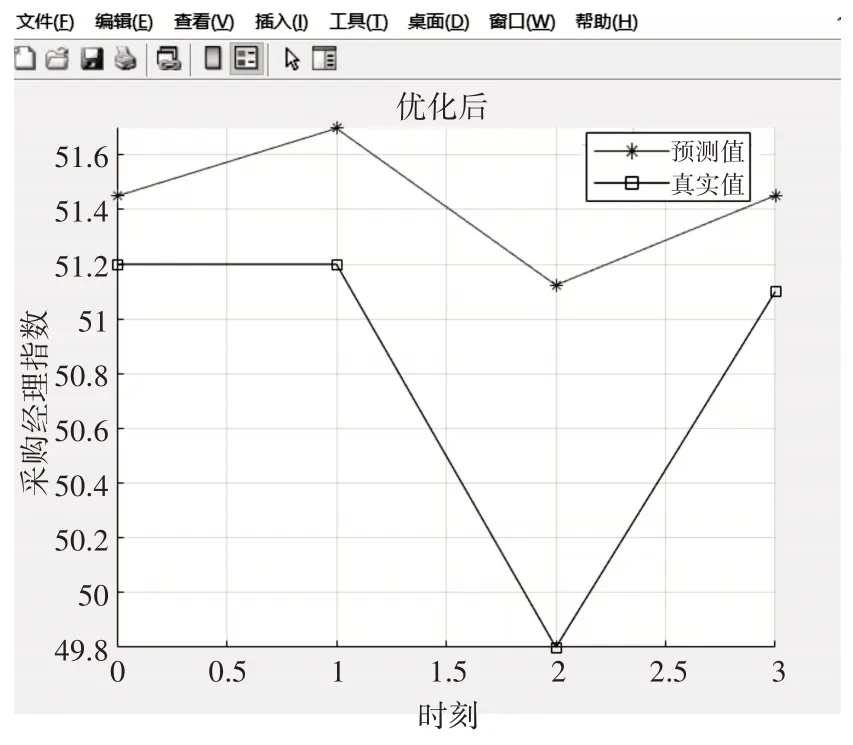
图3 SVM仿真结果

可以看出虽然SVM 能预测指数的涨跌情况，但是预测结果与真实结果存在了一定的差异。这些差异就是没有寻优惩罚系数C和核参数σ所导致的。利用2.3 节中的训练方法，设置粒子群算法寻优的基本参数，设置最大迭代次数K=100 次，种群最大数量sizepop 为20 个，种群最大进化数量为200 个。认知参数C1 的初始值为1.5，社会参数C2的初始值为1.7。用Matlab 进行适应度寻优迭代过程如图4。

图4 PSOSVM寻优曲线

由图4 可知此预测模型迭代到50 次左右达到最优值。根据此模型，在寻优最优参数的基础上，对SVM进行仿真结果如图5。

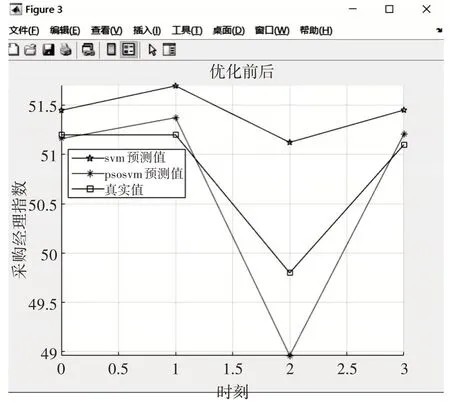
图5 PSOSVM仿真结果

可以看出PSO-SVM 的每次一的预测结果都比SVM 预测结果更加接近真实值，PSO-SVM 的预测准确率较高，与真实值差异小。

4 结语

制造业企业需要能够时刻调整自己的生产规划来适应市场的需求变化，PMI以其可靠性为企业提供了参考。通过对支持向量机参数的寻优，PSO-SVM 算法能够大致判断PMI 的涨跌情况，预测值与实际值相差不大，且PSO-SVM 算法具有较强的稳定性，收敛速度也比传统SVM 快，相比于传统SVM，PSO-SVM 算法能够提供更精准地预测来满足企业的需求。