物流配送中心选址问题研究*

张平东 马 军

（沈阳工业大学管理学院 沈阳 110870）

1 引言

物流配送中心是整个物流系统运作的核心，在物流系统中起着关键性的作用。物流配送中心上游是供应商、厂商等，下游就是需求点、用户，物流配送中心的合理选址直接影响整个物流系统的运作效率［1］。合理的物流配送中心选址可以节约物流运作成本，有效地提高经济效益，保证物流系统的协调运作，对物流行业的发展具有重要意义［2～3］。

近些年，有很多学者研究了物流配送中心选址的问题，其中包括单一配送中心选址问题以及多个配送中心选址问题等［4］，朱晓敏等［5］采用重心法以物流运输成本最小为目标研究了物流园区选址的问题；曹勇锋等［6］将重心法和层次分析法结合起来研究了生活垃圾转运站选址的最佳方案；沙磊等［7］采用非线性规划法研究了铁路应急物资存储仓库的选址问题；刘善球等［8］运用了遗传算法以成本最小为目标研究了快递物流配送中心的最优选址方案；徐利民等［9］则采用动态规划法考虑到时间变动对选址问题的影响，研究了仓库存储中心的最优选址方案。但以上方法都存在一个缺点，那就是精度不高、偏差较大、寻优效果不理想等［10］。针对以上问题，本文提出了粒子群算法和模拟退化算法来优化物流配送中心的选址问题，这两种方法具有适用性强、精度较高、收敛速度快等特点，并通过多次仿真实验得出了两种算法的适用范围，为物流配送中心选址问题提供了新的解决方案。

2 物流配送中心选址模型

本研究是以物流配送中心的总配送量最小为研究目标，分别采用粒子群算法和模拟退火算法在给定物流配送中心数目的条件下，在某一确定范围内确定物流配送中心的最优位置。使得配送中心到已知需求点的总配送量（距离×需求量）达到最小，并且满足各需求点的要求。为了方便建立本文的物流中心选址的数学模型，做出如下假设：

1）各配送中心容量不限，但必须满足各需求点需求；

2）每个需求点只能由一个配送中心负责配送；

3）配送中心到需求点距离为直线距离。

根据以上假设条件，建立物流中心选址的数学模型可表示为

其中：所有需求点的集合用N表示；所有备选配送中心的集合用M表示；需求点i到离它最近配送中心j的距离用dij表示；需求点i对应的需求量为wi；zijϵ{0 ，1} ，zij=1 表示需求点i的需求量由配送中心j负责供应，否则zij=0；配送中心到需求点距离的上限用l表示。

式（1）为目标函数；式（2）表示配送中心的承载容量应该大于或等于需求点的需求量；式（3）表示每个需求点只能由离它最近的配送中心进行配送；式（4）表示每个需求点都会有配送中心进行配送；式（5）表示需求点中被选为配送中心的数量p；式（6）表示在一定的范围内，配送中心可以对需求点进行配送。

3 求解选址问题的算法介绍

3.1 粒子群算法

粒子群算法实质上是模拟鸟类飞行寻找食物的行为，鸟群在飞行中集体协作，使群体效用达到最优化。粒子群算法就是模拟鸟群捕食的行为来解决现实中的优化问题，在迭代过程中，粒子本身找到的最优解叫做个体极值点，用pbest表示其位置；整个种群找到的最优解叫做全局极值点，用gbest表示其位置。粒子就是通过跟踪这两个极值来不断更新寻找方向［11～12］。粒子找到这两个最优解后，根据式（7）和式（8）来更新自己的速度和位置。粒子i的信息可以用D维向量表示，位置表示为Xi=(xi1，xi2，…，xiD)T，速度表示为Vi=(vi1，vi2，…，viD)T，其他向量类似。则速度和位置更新方程为

式中，c1，c2为学习因子，为粒子i在第k次迭代时，速度的第d维分量。rand1，2是分布在[0 ，1]间的随机数。是粒子i在第k次迭代时，位置的第d维分量。

实现过程如下：

第一步：种群初始化；

第二步：迭代设置：设置迭代次数，并令当前迭代次数为1；

第三步：更新粒子的速度向量；第四步：更新粒子的位置向量；第五步：更新粒子的局部最优解和种群的全局最优解；

第六步：终止条件判断：判断是否满足寻优结束条件，如果满足，输出全局最优解，否则继续进行迭代［13］。

3.2 模拟退火算法

模拟退火算法起源于固体退火原理，固体物质通过加温使温度变高，然后缓慢的冷却，此时原子无规则移动、排列重组，可以释放残余应力，消除材料中差排。整个过程实现了固体内部粒子从无序到有序的过程，最终在常温状态下达到基态，内能减至最小［14～15］。目前该算法普遍适用于优化问题的求解。

实现过程如下：

第一步：设定冷却进度表。主要包括冷却开始温度、终止温度、降温函数以及马尔可夫链长度；

第二步：在所建立的数学模型中找出解空间和目标函数，并生成初始解；

第三步：新解的产生与接受和最优解的存储；

第四步：在任一温度下，以第一步设定的马尔可夫链长度重复第三步过程，在按照设定的冷却进度表设置降低温度，直至满足终止温度的要求［16］。

4 案例分析

案例一：为了研究粒子群算法和模拟退火算法在物流配送选址问题的应用，本文以超市物流中心选址问题为例，进行实验仿真研究。设在范围（0，0）到（100，100）的矩形范围内，散布着40 个连锁超市，每个连锁超市的坐标及需求量见表1。

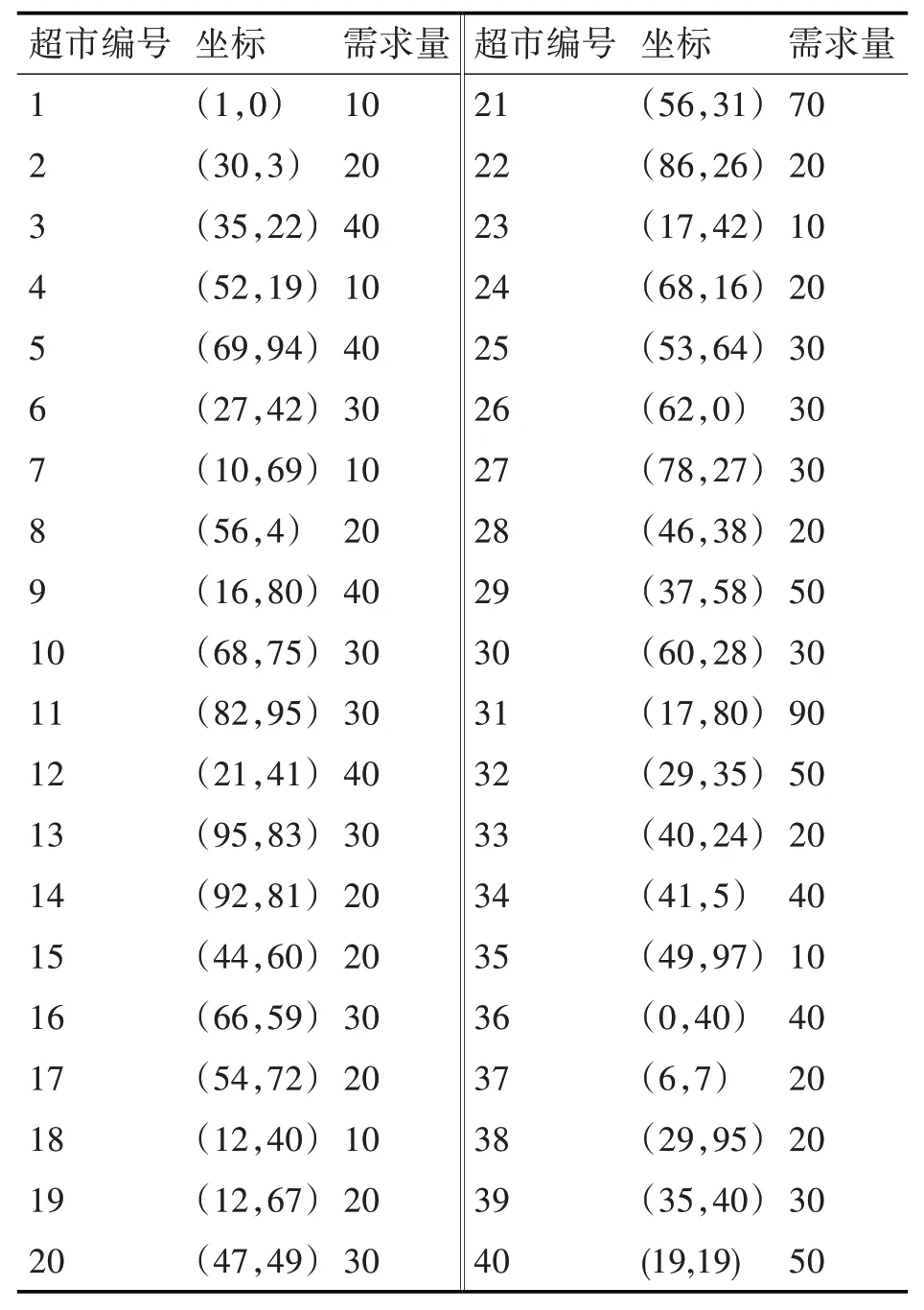
表1 40个连锁超市的坐标及需求量

要求在该矩形区域内选择5 个位置建立物流配送中心。已知各物流配送中心容量不限，并且每个超市只能由一个物流配送中心负责配送，使得5个物流配送中心到所有超市的总配送量（距离×需求量）最小，其中物流配送中心到超市距离为直线距离。

在仿真中，首先采用粒子群算法求解该问题，其中设置学习因子c1=c2=2，粒子群规模为1500，最大迭代次数为50。超市坐标位置图如图1所示，每个圆点表示各个超市的位置。图2 为初始路径图，其中每个小正方形表示物流配送中心，圆点与小正方形之间的连线表示某个超市的物资由该物流配送中心进行配送。具体优化过程见图3。经过50 次迭代，得到图4 的最优路径图，即配送中心为所选配送中心编号（共5 个）：11、15、30、31、32，此时总配送物流量为15896.7738。物流中心选址方案表如表2所示。

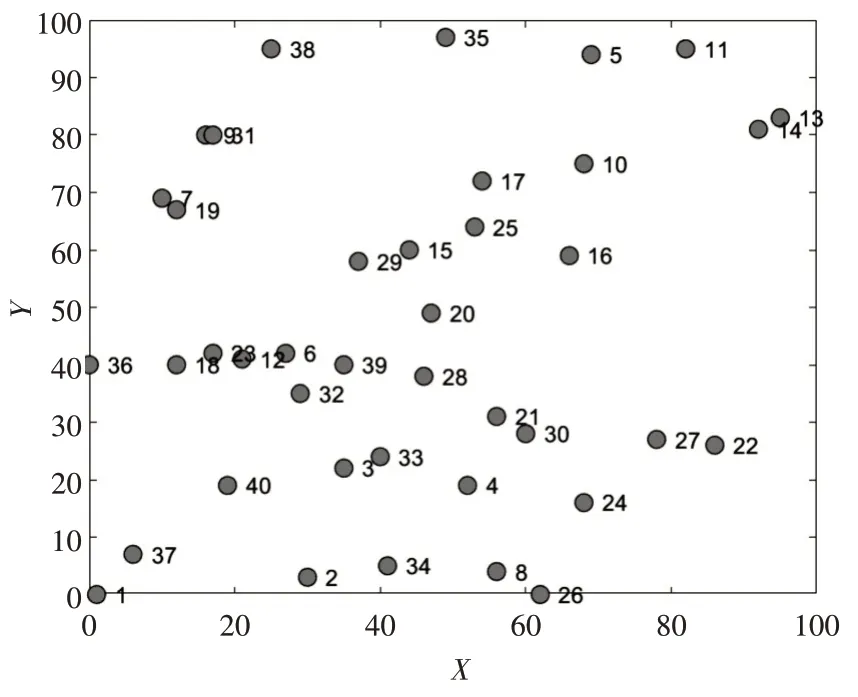
图1 超市坐标位置图

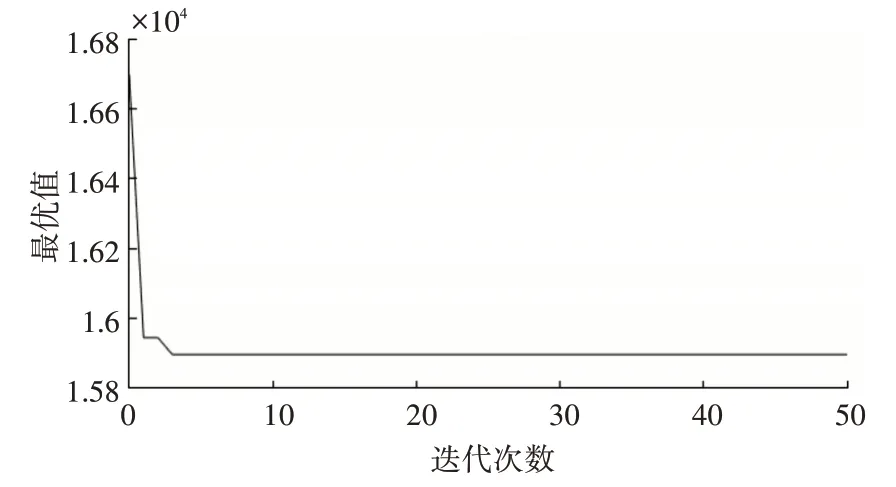
图3 粒子群算法优化过程图

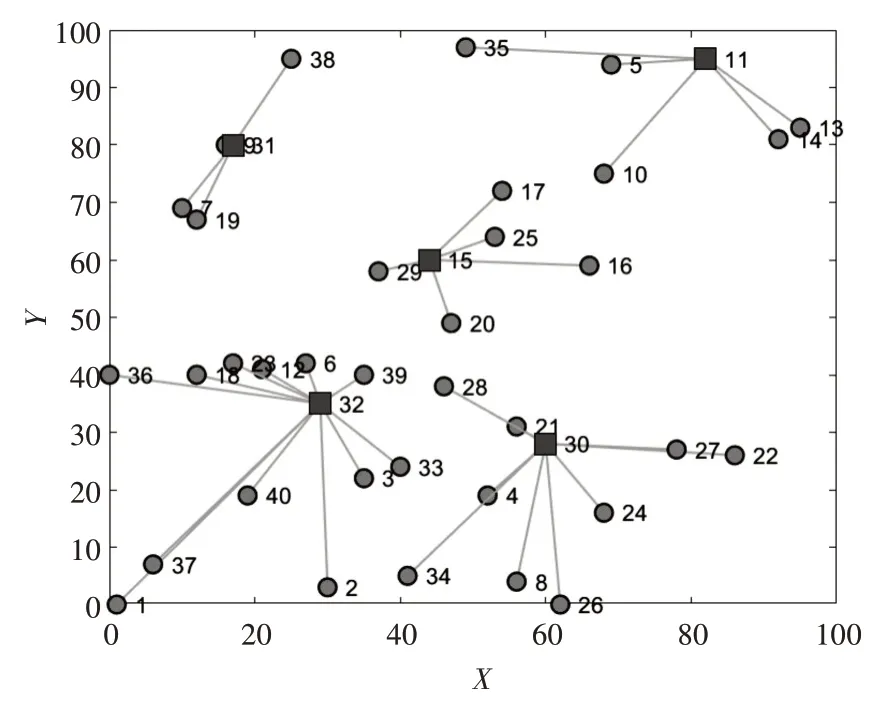
图4 粒子群算法最优路径图

表2 物流中心选址方案表

接着，本文采用模拟退火算法对该问题进行求解，其中设置初始温度值为10000，温度下降速率为0.98，终止温度为0.01，此时算法停止迭代。具体优化过程和最优路径图如图5和图6所示。最后得出配送中心为所选配送中心编号（共5 个）：3 6 10 30 31，此时总配送物流量为16091.7801。物流中心选址方案表如表3 所示，两种算法的选址性能对比分析表，如表4所示。

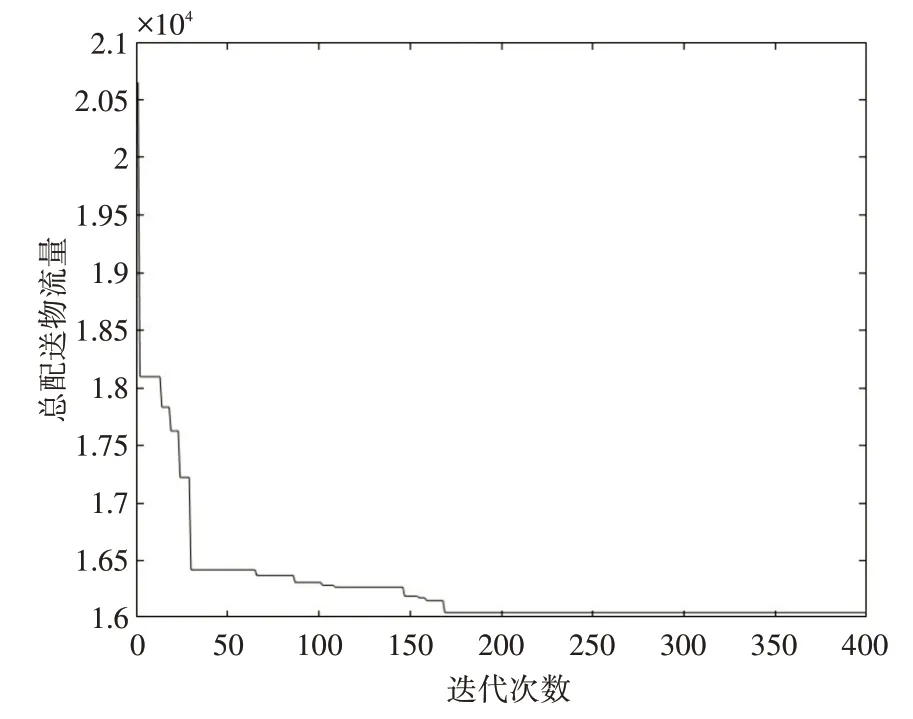
图5 模拟退火算法优化过程图

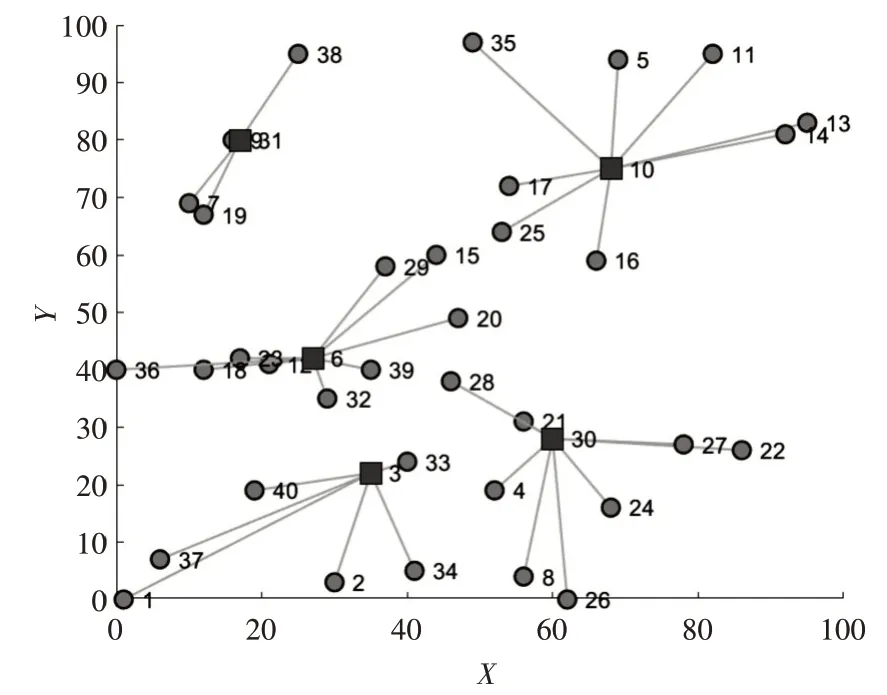
图6 模拟退火算法最优路径图

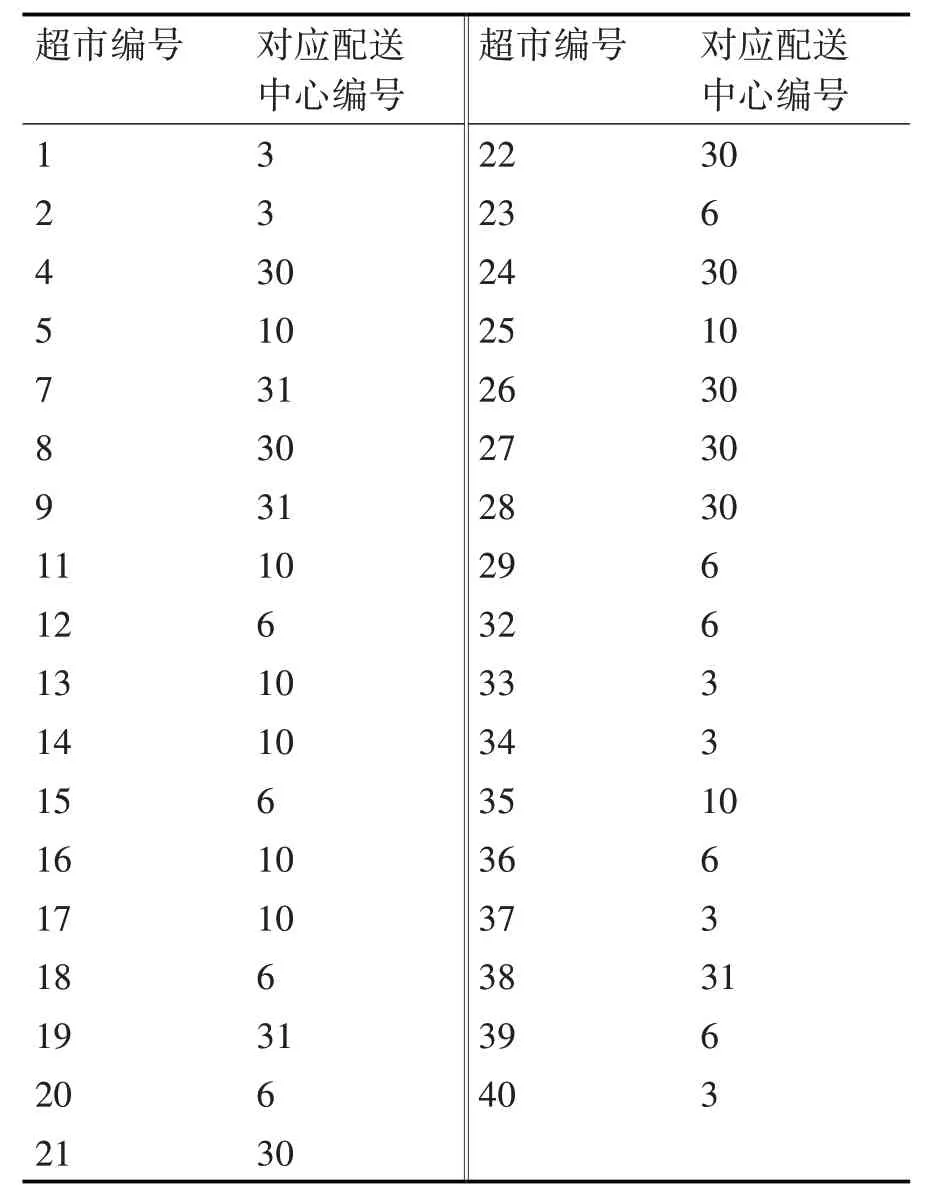
表3 物流中心选址方案表

表4 两种算法性能对比分析表

从表3 可以看出，在40 个连锁超市中确定5 个位置建立配送中心的情况下粒子群算法其整体性能是优于模拟退火算法的。

案例二：为了验证算法性能的普遍性，本文将上述案例中连锁超市的数量增加到80 个，配送中心数量增加到10 个，连锁超市的坐标及需求量如表5所示。

表5 80个连锁超市的坐标及需求量

再次进行仿真模拟，采用粒子群算法经过50次迭代，具体优化过程见图7，图8 为最优路径图，即配送中心为所选配送中心编号（共10 个）：14、18、27、31、48、51、65、70、79、80，此时总配送物流量为22355.5598。

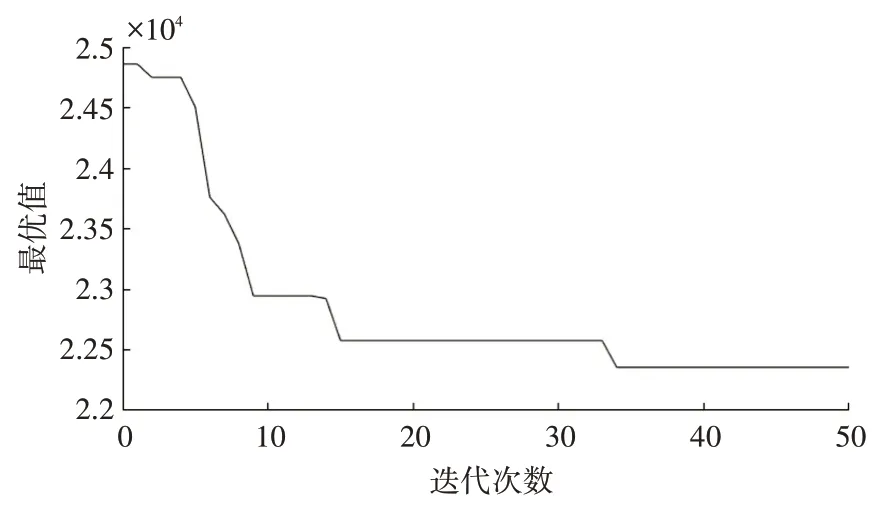
图7 粒子群算法优化过程图

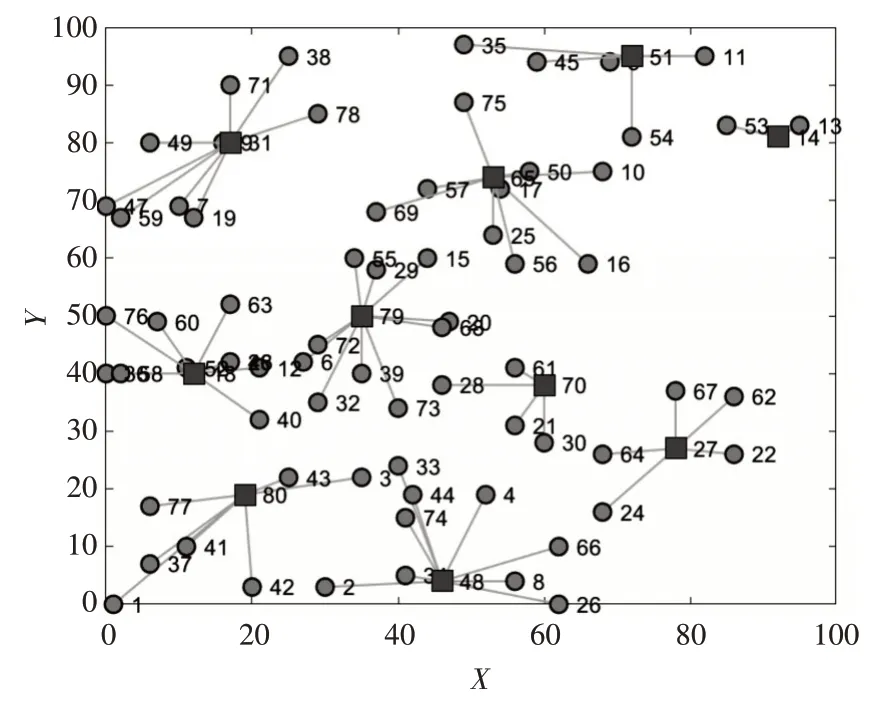
图8 粒子群算法最优路径图

接着采用模拟退火算法求解此问题，具体优化过程和最优路径图如图9和图10所示，并将两种方法性能进行对比，如表6所示。

图9 模拟退火算法优化过程图

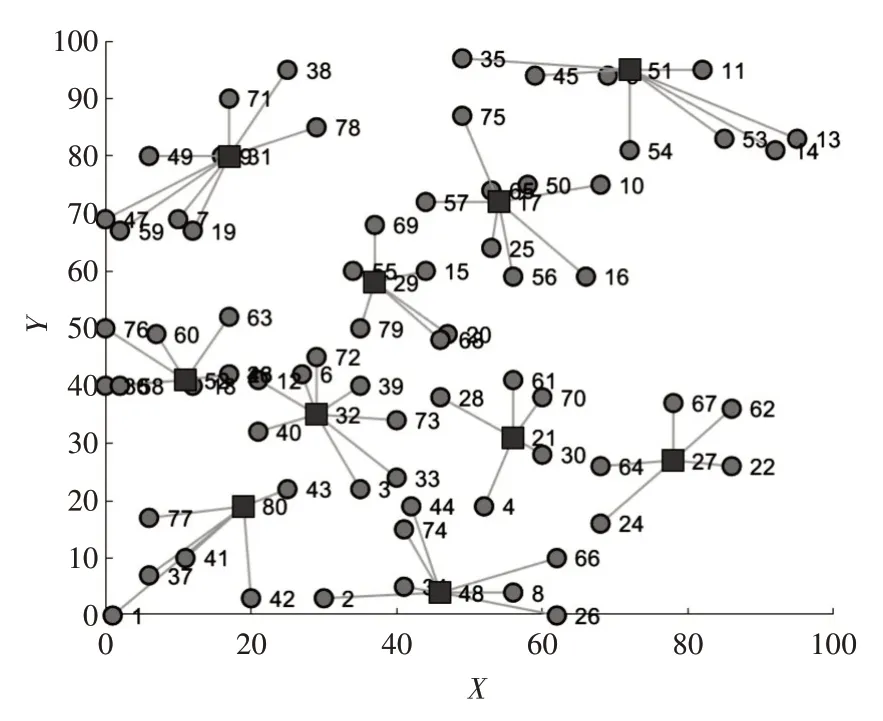
图10 模拟退火算法最优路径图

表6 两种算法性能对比分析表

通过上诉分析，可以看出，在80 个连锁超市中确定10 个位置建立配送中心的情况下，模拟退火算法在求解物流配送中心选址问题上是优于粒子群退火算法的。

案例三：为了更加有效地验证算法性能的适用性，本案例延续案例二的连锁超市坐标和需求量，将连锁超市扩大到100 个，配送中心扩大到12 个，继续进行仿真模拟。增加的20 个连锁超市坐标及需求量如表7 所示。具体优化过程和最优路径图如图11 和图12 所示，两种方法性能对比分析表见表8。

图11 粒子群算法最优路径图

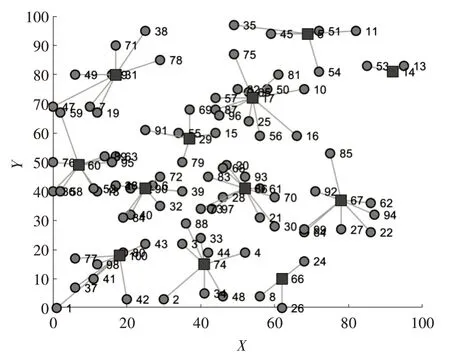
图12 模拟退火算法最优路径图

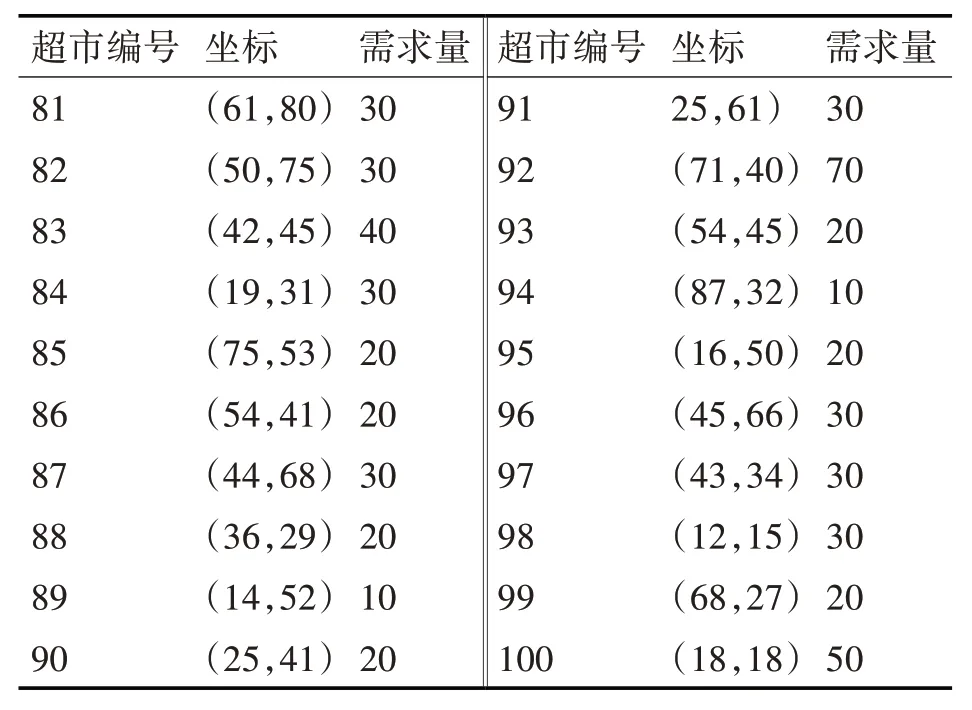
表7 增加20个连锁超市的坐标及需求量

表8 两种算法性能对比分析表

通过上诉分析，可以看出，在100 个连锁超市中确定12 个位置建立配送中心的情况下，模拟退火算法在求解物流配送中心选址问题上也是优于粒子群退火算法的。

5 结语

本文将粒子群优化算法和模拟退火算法引入到求解物流配送中心选址的问题上，两种算法在处理物流中心选址问题上都具有操作简单、收敛速度快、寻优精度高等特点。通过多次仿真模拟实验结果表明，在需求点和配送中心规模较小时，采用粒子群算法求解该问题是优于模拟退火算法的；在需求点和配送中心规模较大时，采用模拟退火算法求解该问题是优于粒子群算法的，并具有一定的普遍性和可靠性，这两种方法都可以精准地在众多需求点中确定物流配送中心的最佳位置。