基于同步提取变换和LightGBM 算法的电能质量复合扰动分类方法研究*

冯 昆 徐天奇 李 琰 何兆磊 朱梦梦

（1.云南省高校电力信息物理融合系统重点实验室（云南民族大学） 昆明 650504）

（2.云南电网有限责任公司计量中心 昆明 650217）

（3.云南电网有限责任公司电力科学研究院 昆明 650217）

1 引言

随着电网中高铁、电弧炉等大量非线性负荷的快速发展以及大功率电力电子设备的大规模使用，使得电网的负荷端变得日趋复杂。由此将降低电网的电能质量，影响电网运行安全。智能电网发展中的一个关键挑战就是提高供电质量。电力系统扰动的监测和分析对于查明系统异常运行的原因、评估保护、制定控制方案以及确保系统快速恢复非常重要。并且准确识别电网中的各类扰动是改善电能质量的必要前提和基础［1～3］。

电能质量扰动的判别通常有特征提取和模式识别两个步骤。需要通过信号处理技术对原始信号进行初步的分析，将原始信号分解成若干子信号对每个子信号进行特征提取［4］。主要的方法有模态分解、傅里叶变换、S 变换、短时傅里叶变换、小波变换系列等［5］。快速傅里叶变换FFT（Fast Fourier Transform）通常用来表征平稳信号的频谱和谐波，但由于其固定的窗函数，因此不适合识别非平稳信号特征。短时傅里叶变换STFT（Short-Time Fourier Transform）的分解效果受窗函数的影响较大。小波变换WT（Wavelet Transform）是在STFT的基础上发展而来，用于改进固定分辨率的问题［6］，但分解效果同样受所选小波母函数的影响较大，容易出现模态混叠现象，影响特征的提取。同步提取变换SET（Synchroextracting Transform）［7］是在同步挤压变换SST（Synchrosqueezing Transform）基础上提出来的一种新的时频分析方法。SST 仅考虑频率/尺度方向上的系数压缩，会出现能量发散，在噪声环境下会有较大影响，而SET是利用在瞬时频率位置的时频系数产生时频谱，使其获得更好的噪声鲁棒性，运算速度上也有很大的优势［8］。

特征提取完后使用机器学习或深度学习进行分类。文献［9］使用改进HHT 和决策树进行扰动信号的分类，仅实现了五种单一扰动和两种双重扰动的分类，可识别的扰动类型较少，远不能满足电网的需求，并且在一定程度上受噪声的影响较大。文献［10］利用二维灰度图和卷积神经网络进行特征提取和分类，但神经网络在电能质量扰动识别中的学习速率和分类效果易受网络结构、权值自适应算法和噪声强度的影响，并且仅实现单一扰动，难以适应复杂的多重扰动。文献［11］用极大重叠离散小波变换和并行隐马尔科夫模型进行分类识别，虽然训练时间较短，但分类准确率却很低，并且10类事件类型没有考虑噪声对分类准确率的影响。LightGBM（Light Gradient Boosting Machine）是一种boosting集成学习算法。在工业大数据应用场景中具有运算速度快，运算效率高的优势，在故障预测［12］，电动机故障诊断［13～14］等领域已有了很好的应用效果。

针对信号分解出现的“模态混叠”和扰动识别种类较少，分类准确率较低的问题，提出了一种基于同步提取变换，复合多尺度排列熵，PCA（Principal Component Analysis）降维和LightGBM 算法的电能质量复合扰动分类方法，首先对7 种单一扰动、6种二重扰动进行同步提取变换，提取子信号时域、频域特征，及复合多尺度排列熵变换得到的特征矩阵，对特征矩阵进行PCA 降维以减小运算复杂度。用所构造的特征集合训练LightGBM 分类器进行分类。与现有的XGBoost，Catboost 和随机森林算法进行分类准确率和耗时比较，验证所提方法的有效性。

2 同步提取变换和复合多尺度排列熵的扰动信号特征提取

2.1 同步提取变换基本原理

假设一个信号s(t) ，其标准表达式为［15］

式中g(u-t) 为窗函数。令gw(u)=g(u-t)·。由Parseval定理，STFT公式可以表示为

信号s(t)傅里叶变换后为式中的为(gω(u) )傅里叶变换的复共轭。

使u-t=t′，((u) )的频域形式则有：

即可得到：

STFT公式乘一相位因子eiωt时，式（4）可表示为

令u-t=τ，则STFT可改写为

若一信号的频率为ω0，其频域可表示为

将式（7）带入式（5）中可得到：

由于窗函数在频域中是紧支撑的，且在0 频率处有ĝ(ξ)≤ĝ(0)。因此，在频谱Ge(t，ω)中当ω=ω0时，时频系数具有最大的幅值A·ĝ( )0 ，STFT 谱中时频系数的立即频率为

其中，∂tGe(t，ω) 是Ge(t，ω) 对时间的一阶导数。为了得到精确的立即频率估计，可进行计算得：

在二维时频平面中，可以得到一个新的时频谱ω0(t，ω)，并且与STFT 的谱系数Ge(t，ω)是一一对应的。同步提取变换仅提取STFT谱在瞬时频率位置的时频系数，公式可表示为

其中δ(ω-ω0(t，ω) )称为同步提取算子。

2.2 同步提取变换的扰动信号分解实验

为比较说明同步提取变换的信号分解能力，设置扰动信号包含幅值为1 的50Hz 基波、幅值为0.2的3 次、5 次、7 次、9 次、11 次谐波，并加上30dB 的噪声分量。

利用CEEMDAN 分解扰动信号如图1，由图可知基波信号被分解到IMF7中。但受到噪声信号的干扰，谐波信号出现了很大程度的变形，难以区分各次谐波信号，并且虚假分量较多。

经实验对比，选用“db10”母小波进行小波变换六层分解，能较好分离出基波信号，分解扰动信号如图2。由图可知IMF1为基波信号，IMF2-IMF4为扰动信号谐波分量，但是出现了严重的“模态混叠”现象，小波变换在噪声环境下难以准确分解谐波信号，IMF5-IMF6为噪声分量。

图2 小波变换分解图

利用SET 分解扰动信号，将分解层数设置为6层，窗长度选为800，分解结果如图3，由图3可以观察到基波被分解到IMF1 中，谐波信号被分解至IMF2-IMF6 中，谐波子信号不存在“模态混叠”现象，各个分量分解幅值也较为精准。由于SET是利用在瞬时频率位置的时频系数产生时频谱，即使在噪声背景下，SET仍然有不错的分解质量。

图3 扰动信号SET分解

2.3 多尺度排列熵算法

多尺度排列熵（Multiscale Permutation Entropy，MPE）是一种度量时间序列复杂程度的方法，具有非线性单调变换不变的特点，所以适应于对SET分解后的子信号进行时间复杂度排列，更好的区分不同扰动信号的特征。具体步骤如下［16］：

1）将原始信号的时间序列{x(i)，i=1，2，…，N}，粗粒化时间序列通过式（12）进行构造：

其中：τ是尺度因子。τ=1时粗粒化序列为信号的原时间序列；τ＞1 时原始时间序列被粗粒化成长度为p=[]的τ个粗粒化序列，…，[·]表示取整。

2）计算每个尺度因子τ下的排列熵值，得到给定的所有尺度因子的排列熵值。若尺度因子较大，原始序列长度较小，粗粒化序列的长度则相对较小，在尺度较大时，时间序列的所包含的信息则会减少。排列熵值越小，则表明原始信号时间序列越规整。

2.4 复合多尺度排列熵算法

CMPE（Composite Multiscale Permutation Entropy）将MPE 的单一粗粒化改进为复合粗粒化。其具体计算步骤如下［17］：

1）序列{x(i)，i=1，2，…，N}通过式（13）定义粗粒化序列即：

表示尺度因子τ下的第k个粗粒化序列，j表示的第j个点。

2）对于尺度因子τ，计算该尺度因子下每个粗粒序列的排列熵（PE），再对τ个PE 值求平均，则得到CMPE在尺度因子τ下的值，即：

式中m为嵌入维数；λ为延迟时间。

图4 为原始信号时间序列被分为两个粗粒化时间序列。

图4 第二尺度因子下的粗粒化过程

2.5 其他特征提取

除复合多尺度排列熵外本文还对SET 分解后的子信号提取最大值、最小值、峰值、峰峰值、均值、平均幅值、方根幅值、方差、标准差、有效值、峭度、偏度、波形因子、峰值因子、脉冲因子、裕度因子、余隙因子中心频率、小波能量比、过零点次数、希尔伯特变换后的瞬时幅值曲线能量、希尔伯特变换后的瞬时幅值曲线标准差、希尔伯特变换后的瞬时频率曲线标准差、与标准信号分解的子信号能量分布的差异、总谐波畸变率、小波尺度熵、小波奇异熵。利用这些特征构造信号的特征集。

3 LightGBM模型训练

传统的boosting集成学习算法能提高单个模型的分类准确率和模型的泛化能力，具有训练效果好，不易过拟合等优点。但是在每一次的迭代运算中都需要遍历训练数据多次，增加了模型训练的时间，因此难以适应于数据量巨大的电力系统。LightGBM 解决了GBDT（Gradient Boosting Decision Tree）解决海量数据时所遇到的问题，更加适用于电能质量扰动分类识别。

3.1 LightGBM的直方图算法

LightGBM 用直方图算法代替了xgboost的预排序算法，将特征值离散成K个整数，并构造宽度为K的直方图。在遍历时，根据直方图的离散值，找到最佳分割点［12］，直方图算法如图5。同时LightGBM 还拥有带有深度限制的按叶子生长（leaf-wise）算法如图6。数据经过Level-wise 的同时分裂同一层的叶子，进行多线程优化。Histogram还可以做差加速，如图7，父节点与子节点的直方图做差，可以得到子节点兄弟节点的直方图，直方图做差仅需遍历直方图的k个桶。利用做差加速，LightGBM极大提高了运算效率。

图5 直方图算法

图6 Leaf-Wise生长策略

图7 直方图做差加速

3.2 LightGBM 的单边梯度抽样算法和互斥特征捆绑算法

单边梯度抽样算法GOSS（Gradient-based One-Side Sampling）仅保留了梯度较大的样本，并对梯度较小的样本进行随机抽样，为了不改变样本的数据分布，在计算增益时为梯度小的样本引入一个常数进行平衡。通过GOSS，LightGBM 减少了样本的数量，提升了训练的速度。

高维度的数据大都具有稀疏性的特点，EFB（Exclusive Feature Bundling）将一些互斥的特征捆绑在一起，这样两个特征捆绑起来不会造成信息的丢失。EFB 算法利用特征和特征间的关系构造一个加权无向图，并将其转换为图着色的问题来求解，求解过程中采用的贪心策略。EFB在保证精度的同时提升了算法的效率［18］。

4 实验分析

参照文献［5］仿真生成标准信号（C0）、暂升（C1）、中断（C2）、暂降（C3）、谐波（C4）、暂态振荡（C5）、暂态脉冲（C6）、电压闪变（C7）7种单一扰动，中断加暂态震荡（C2+C5）、谐波加暂态振荡（C4+C5）、谐波加暂态脉冲（C4+C6）、谐波加闪变（C4+C7）、暂态振荡加闪变（C5+C7）、暂态脉冲加闪变（C6+C7）6 种双重扰动。每类扰动随机生成600 条实验数据，采样频率为6.4kHz，采样长度为2048 个采样点。实验采用十折交叉验证。

将构造的14 类信号进行SET 分解后提取上述复合多尺度排列熵在内的特征构成特征集，复合多尺度排列熵的嵌入维数选择为6，尺度因子设定为12。由于复合多尺度排列熵的维数较高，使用PCA对其进行降维运算，提取3 个主元分量，以减少特征的复杂程度。在LightGBM 中进行分类实验，为说明本文算法的优势将构造的特征集用XGboost，CATboost，随机森林进行对比实验，为证明本文所提方法的在噪声环境下的分类效果，在原始扰动信号中分别添加30dB、40dB、50dB 噪声，分类结果如表1。分类准确率对比实验结果如表2。训练及分类总时间对比实验结果如表3。

表1 不同噪声环境下本文所提方法分类准确率

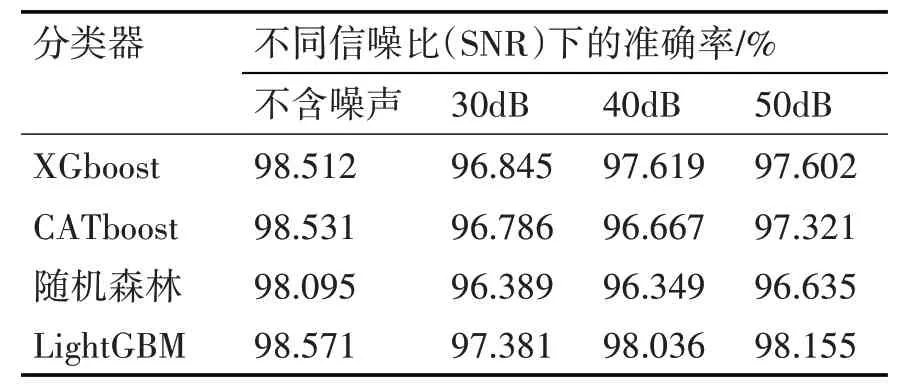
表2 不同分类器平均分类准确率对比

表3 不同分类器不同噪声环境下训练及分类耗时对比

由表1～3 可得本文所提方法的复合电能质量扰动可达98.571%，在30dB～50dB 的噪声环境下准确率也没有大幅度下降，最低仍有97.381%，仍然有较高的准确率，2 重和3 重扰动也有不错的准确率。与不同的分类器对比在训练耗时和分类准确率上有显著的优势。boosting集成学习算法对比随机森林的分类准确率较高，但是CATboost 的训练和分类所需的时间较长。

选择使用4 种不同信号处理方法的参考文献与本文所提方法做比较如表4，本文所提方法可以实现的分类类别更多，并且在噪声环境下，准确率没有明显下降。表中-表示文献未提及。

表4 电能质量扰动分类算法性能比较

5 结语

针对电力系统复合扰动分类问题，本文提出了一种基于同步提取变换、复合多尺度排列熵、Light-GBM 的新方法，利用同步提取变换能准确进行扰动信号的分解，提取用PCA降维后的复合多尺度排列熵在内的多种信号特征，构造成特征集，利用LightGBM算法进行分类试验，所提方法对比于XGboost，CATboost，随机森林，具有较好的分类准确率，并且在运算效率、分类耗时上也有显著优势。在原始信号中加入3 种噪声分量分类效果并没有显著下降，具有一定的抗噪性。与其他文献相比提高了识别的种类和噪声环境下的准确率。