一种求解团簇优化问题的混合进化算法*

向 垚 郑斯瑞 赖向京

（南京邮电大学先进技术研究院 南京 210023）

1 引言

全局优化问题广泛存在于各个领域，其中通过搜索原子团簇势能函数的全局最小值，是计算化学领域中一个著名的全局优化问题。在计算化学领域，原子团簇的许多物理和化学性质是由其几何结构决定的，因此确定它们的基态结构对于理解它们的各种性质具有重要意义［1］。由于团簇的局部最优结构的数量随团簇规模呈指数型增长，确定原子团簇基态结构（即团簇的几何优化）是一项非常具有挑战性的任务。事实上，原子团簇优化问题也已经被证明为NP-hard问题［2］。

原子团簇的结构优化问题由于其NP-hard 特性和应用价值，受到了许多研究者的广泛研究。在文献中已有大量相关算法被提出，这些方法可以分为两种，包括基于单解的算法和基于种群的算法。对于基于种群算法，具有代表性的算法包括随机隧道优化算法（Random Tunneling Algorithm，RTA）［3］，自适应免疫优化算法（Adaptive Immune Optimization Algorithm，AIOA）［4］，构型空间退火算法（Conformational Space Annealing，CSA）［5］，基于种群的盆地跳跃算法（Population Basin Hopping，PBH）［6］等。对于基于单解的算法，具有代表性的算法包括basin-hopping 算法（BH）［2］，带有表面算子和内部算子的启发式算法（Heuristic Algorithm with the Surface and Interior Operators，HA-SIO）［7～8］，动态格子搜索算法（Dynamic Lattice Searching，DLS）及其变种［9～11］，和模糊全局优化算法（Fuzzy Global Optimization，FGO）［12］等。

PBH算法是一种混合进化算法，在许多全局优化问题上表现出了很高的性能，例如圆形packing问题［13］。本文通过整合PBH 算法的框架和基于连通表（Connectivity Table，CT）［4］的距离函数，为Gupta 势能函数建模的原子团簇的结构优化提出了PBH算法的一个变种，并将该算法成功应用于银团簇的结构优化。计算结果很好地表明了该算法的有效性。

2 Gupta势能函数模型

Gupta 势能［14］常用于给金属团簇建模，其势能函数具有如下形式：

其中N为原子数目，rij为原子i与原子j之间的欧式距离，r0为团簇两原子之间的平衡距离，r0=1.0，A，p，q，UN为势能函数的参数，这些参数的不同组合能表示不同类型的原子团簇。对于银团簇，其相应的参数取值如下：

3 基于连通表的种群盆地跳跃算法（PBH-CT）

3.1 PBH-CT算法的主框架

本文提出的PBH-CT 算法是一种混合进化算法，它由一个种群初始化方法、一个局部优化方法，一种扰动算子和一个种群更新策略组成，其伪代码如算法1所述。

从一个随机生成的m个个体构成的初始种群开始，算法执行若干次迭代，直到连续MaxNoImp次迭代无法改进当前最好解为止，其中MaxNoImp 是一个参数。在每个迭代，首先找到种群X中与当前解Yk距离最近的构型Xr，然后通过将两个构型之间的距离与接收罚值dcut进行比较，来判断当前构型Yk是否与种群X的解Xr相似。

若d(Yk，Xr)＞dcut，则表示两个构型Yk与Xr是不相似的。此时，我们比较Yk与种群X中的最差构型Xw的目标函数值；若E(Yk)＜E(Xw)，则用Yk替换种群X中的Xw；若d(Yk，Xr)≤dcut，则认为两个构型是相似的，此时，我们比较这两个构型的目标函数值；若E(Yk)＜E(Xr)，则用Yk替换种群X中的Xr。

3.2 初始种群

在基于种群的算法中，种群的多样性对算法性能起着关键作用。因此，为了保证初始种群X的多样性，本文采用了如下的初始种群策略：随机生成m个构型来构成初始种群，每个个体都是在一个半径为R=（3N/（4Π））1/3·r0的球体中随机撒入N个原子中心点，从而得到一个随机构型，并通过局部优化方法对该构型进行局部优化，从而得到初始种群X。在本文算法中，局部优化方法采用的是L-BFGS［16］算法，其中L-BFGS 算法是一种高效的局部优化算法，已被广泛应用于可导函数的局部优化。

3.3 扰动

对于团簇优化问题，其势能函数具有大量的局部最优解，且局部最优值的个数随着原子个数N呈指数关系增长。因此，对于规模较大的算例，如何跳出这些局部陷阱变成了解决团簇优化问题的主要难点。为了避免陷入局部最优陷阱，本文采用经典的随机扰动策略。具体而言，给定一个候选解x=(x1，x2，…，x3N)，通过随机小扰动来生成后代解，即xi←xi+rand(-Δ，Δ) (1 ≤i≤3N)，其中rand(-Δ，Δ)表示[-Δ，Δ]中的一个随机数，Δ 是一个参数，在本文中设置成0.7。

3.4 构型间的距离函数

在该算法中，采用团簇的最近邻接数（记为nnn）和连通表（CT）［4］来定义两个团簇构型的距离函数d（A，B），具体而言，对于一个团簇来说，nnn的定义如下：

其中rij表示原子i和原子j之间的欧式距离，r0为原子间的平衡距离。

另外，CT 是一个基于团簇构型的拓扑信息的向量，由团簇中原子的最近邻居个数生成。CT 为14 维向量，其中CT［i］（1 ≤i≤14）表示在团簇中有i个邻居原子的原子个数。值得注意的是，在所研究的原子团簇中，原子的最近邻居数均不超过14。

借助连通表（CT）和最近邻接数（nnn），可以如下定义团簇构型A和团簇构型B之间的距离函数d（A，B）：

其中，（或）是构型A（或B）的最近邻接数。CT（Ai）（或CT（Bi））是构型A（或B）中有i个邻居原子的原子个数。

4 实验结果与比较

4.1 实验条件

本文算法通过C 语言实现，并在Windows 10操作系统、主频为2.5GHz、内存为8GB 的PC 机上进行实验。算法参数设置如下：m=20，MaxNoImp=400。另外，由于算法的随机性，对于n∈［10，61］范围内的每个银团簇，本文算法独立地运行了10次。

4.2 实验结果

实验结果总结在表1 中，其中第1 列给出了团簇中的原子个数（N），第2 列给出了文献中已知的最优解，本文所提出的算法的计算结果在随后3 列中给出，包括算法的最优解，达到最优解所需要的平均计算时间和达到最好解的成功率。

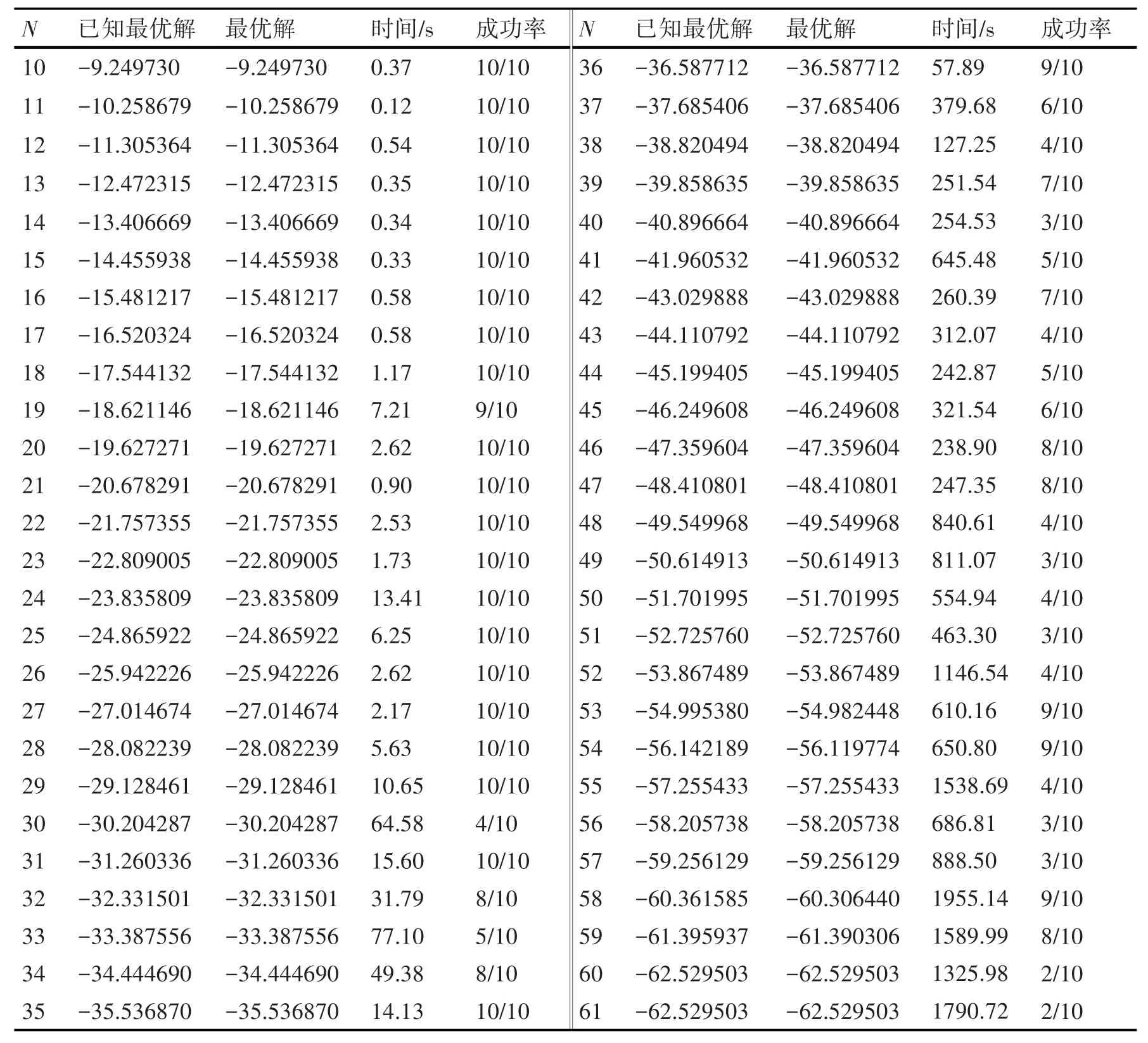
表1 计算结果与当前文献中最好的结果比较，其中最好的结果来自参考文献［3］和［9］

从表1 中可以看出，所提出的算法在大多数测试的算例中都可以找到当前文献中最好的结果，这表明所提出的算法在10 ≤N≤61 的范围内具有强的搜索能力。然而，该算法在4 个难例（即Ag53、Ag54、Ag58、Ag59）上未找到当前已知的最优结果，其计算结果在表1中用斜体表示。

对于10 ≤N≤29 的小团簇来说，所提出的算法在平均计算时间和算法成功率上都具有较高的性能。但是随着原子个数N的增加，算法的计算时间会显著增加。

另外，为了直观地表示计算结果，我们在图1中分别给出4 个代表性团簇构型的最优构型的图形。如图1所示，Ag33的构型是基于十面体的结构，Ag39的构型是基于面心立方体（FCC）的结构，Ag46的构型是无序形态的，而Ag49的构型是基于二十面体的结构。

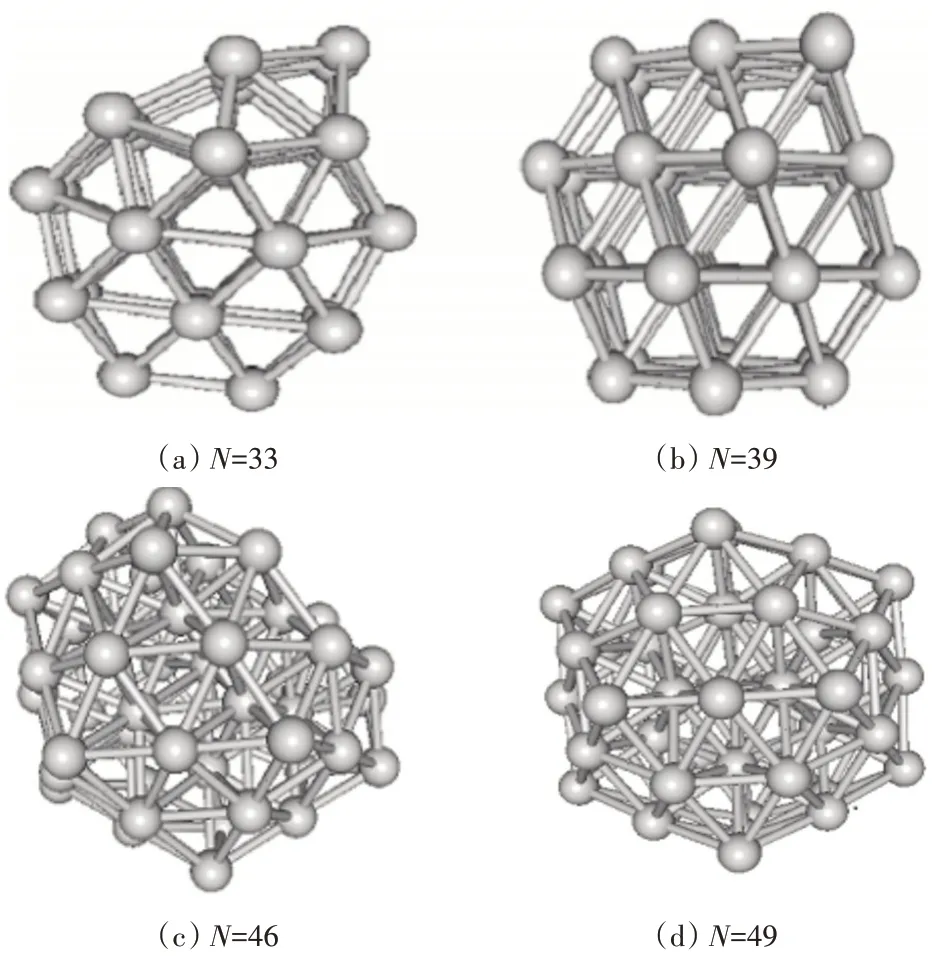
图1 4个代表性算例的最优构型

5 结语

本文针对Gupta 势能描述的银团簇的结构优化问题，提出了一个PBH 算法的新变种，并对原子数在10 ≤N≤61范围内的银团簇进行了优化。与文献中已有的PBH 算法不同的是，本文提出的PBH 算法的变种利用了连通表来定义团簇构型间的距离函数。计算结果表明，该算法对于Gupta 势能描述的银团簇的结构优化是有效的。具体而言，在10 ≤N≤61范围内，提出的算法能够获得除4个难例以外的已知全局最优构型。实验结果再次表明，连通表是定义团簇构型间距离函数的一种很好的工具。在将来，我们打算在其他原子团簇上验证它的有效性。