含CVaR 及增广ε-约束法的多目标光储充电站容量优化配置

黄婧杰，李金成，刘科明，任一鸣，杨洪明，周任军

（1.湖南省清洁能源与智能电网协同创新中心（长沙理工大学），长沙 410114；2.中车株洲电力机车研究所有限公司，湖南 株洲 412001）

0 引言

在双碳目标驱动下，电动汽车（electric vehicle，EV）和充电站行业发展迅速，耦合了光伏和储能的光储充电站因具有就地消纳光伏、直接降低碳排放等优点而受到广泛关注［1-2］。

在规划建设光储充电站时，投资商注重光储充电站投运过程中的收益。合理的光伏和储能容量大小及配比，不仅能够降低光储充电站的设备投资或者运行成本，还能通过提升光伏消纳空间［3-4］、降低购电功率曲线的峰谷差［5］等降低运行成本。然而光伏出力和EV 充电需求的不确定性会影响光储充电站的容量配置，并进一步影响光储充电站投资商的投运过程的收益［6-7］。因此，利用机会约束规划将不确定性规划转化为确定性规划，降低了投资成本［6］，从而减小投资回收期实现了光储充电站投资运行的经济性［7］。但是，在大多数规划运行中投资商还会面临不确定性导致的收益的波动［8-9］。在光储充电站的规划中这一风险是由光伏出力和EV 充电需求的不确定性造成的，忽略该波动将影响投资商对投运过程收益的估计，因此需要量化收益的CVaR值，并衡量其对收益的影响程度。

处理风险的主要方法有：方差法、风险价值（value at risk，VaR）和条件风险价值（conditional value at risk，CVaR）等［10-12］，其中CVaR 具有良好的数学性质，在满足次可加性、一致性公理的情况下，能准确量化不确定量在给定概率分布下的尾部风险，已在电力系统规划和优化调度方面得到大量应用。如：综合能源系统规划和虚拟电厂容量配置时，采用CVaR 度量可再生能源出力和负荷变动以及电价波动的不确定性带来的运行成本风险［13-14］；风电系统安全经济调度时，采用CVaR 度量不确定性因素给电网安全运行带来的风险［15］。

含风险管理的研究都是通过优化复合目标函数来实施的。其中，处理风险项的传统方法是用一个加权因子将其线性加权到目标函数中，并提供主观设定的不同加权因子下的解集和方案［13-14］。但采用线性加权法处理多目标问题时并不能保证得到最优分布的pareto 解集，而增广ε-约束法能够保证在求解多目标优化问题时，得到的pareto 解集具备更良好的分布性［16-18］、边界最优性，能够映射出多目标问题的实际pareto 前沿，为投资商提供更易调控收益和CVaR 解集梯度的投资方案。故采用增广ε-约束法处理多目标优化问题，为投资商提供不同收益、CVaR 组合投资方案的同时，通过熵权-TOPSIS法为投资商筛选出客观决策方案。

综上分析，为量化收益的CVaR 值，建立含收益和CVaR 多目标容量的配置模型，提出增广ε-约束法处理收益和CVaR 的多目标模型，优化光储充电站的容量配置，量化投资商收益低于预期的CVaR 的值，为投资商提供客观的规划方案及运行策略。

1 EV充电需求及光储充电站函数

1.1 EV不确定性充电需求函数

EV 的充电需求由充电初始时间、充电初始荷电状态（state of charge，SOC）决定，而EV 充电初始SOC值近似服从对数正态分布，充电初始时间近似服从正态分布［6，19］。

式中：SOC1为EV充电初始SOC值；t1为充电初始时间；和分别为EV 充电初始SOC 变量对数的平均值和标准差；和分别为EV 充电初始SOC变量对数的平均值和标准差。

1.2 光伏典型出力函数

式中PPV(t)、PPV、per(t)分别为t时刻的光伏输出功率、光伏配置容量、t时刻的光伏出力百分比。其中，光伏四季典型出力百分比如图1所示［20］。

图1 光伏四季典型出力百分比Fig.1 Typical output percentage of PV in four seasons

1.3 储能电池容量功率函数

储能电池能够在电价低谷期或者光伏发电功率大于EV 充电功率时存储电能；在光伏发电功率低于EV充电功率时释放电能，满足EV的充电需求。

式中WESS、PESS分别为储能电池所配置的容量和额定功率。式（4）为储能容量和功率的约束关系。

1.4 光储系统投资维护成本函数

光储系统投资维护成本包括等年值初始投资成本和年维护成本两个方面。

式中Ccost、Cinv、COM分别为光储系统投资维护成本、光储系统等年值投资成本、光储系统的年维护成本。

1.4.1 等年值初始投资成本Cinv

式中：CPV、CESS，W、CESS，P、CRF分别为光伏单位容量投资成本、储能系统的单位容量投资成本、储能系统的单位功率投资成本、等年值投资系数；r、m分别为贴现率和对应系统的使用年限。

1.4.2 年维护成本COM

2 计及CVaR的光储充电站多目标函数

2.1 场景说明

包含光伏出力、EV 充电需求等不确定量的光储充电站多目标容量优化配置问题属于随机规划问题。场景法处理光伏出力、EV 充电需求的不确定性，通过大量场景模拟各种可能会出现的情况，最终将随机规化问题转化为确定性规划问题［10，13-14］。设定光伏出力场景集S={si，i=1，2，…，nS}，EV充电需求场景集E={ej，j=1，2，…，nE}，其中nS和nE分别为光伏出力、EV 充电需求的总场景数量。

2.2 光储充电站的收益

光储充电站的收益包括投资维护成本和年运行收益两个部分。其中，年运行收益为各场景年运行收益与其概率乘积之和。因此，最大化光储充电站收益的优化问题，得到的收益为期望值［9］。

2.3 总收益的CVaR值

CVaR 是在VaR 理论基础上发展出来的。VaR是指在一定的置信水平下，某一金融投资在未来时段所面临的损失阈值。CVaR 则是当损失大于VaR时，面临的平均损失［21］。CVaR 不仅可用于量化成本型函数的损失，也可以用于量化效益型函数的收益问题，类似于求解电网安全裕度［15］、新能源厂商的收益［8］、风电企业利润［9］等效益型问题。

而收益的CVaR 值指的是在一定置信水平下收益不超过VaR 的预期收益，即通过收益的CVaR 值量化预期收益过低的值［8-9］。

式中：α为置信水平；VaR为总收益小于或等于y时的最大值，此时概率小于或等于1-α［8-9］。

因此，总收益的CVaR值CVaR为［8-9］：

式中：zs，e为虚拟变量；ρ为场景序号（ρ=1，2，…，nSnE）。CVaR衡量了场景（s，e）中光伏出力和EV 充电需求不确定性给投资商收益带来的风险，与各场景的概率π(si)、π(ej)及随机变量有关，而受不确定性量条件复杂与否的影响较小。如果场景（s，e）的收益大于VaR，则zs，e等于0；对于其他场景，zs，e等于VaR与相应场景的收益差［9］。

2.4 含风险偏好系数的多目标处理方法

本文的多目标包括光储充电站收益和收益的CVaR 值。求解计及CVaR 的多目标优化问题时，多使用线性加权法［13-14］，引入风险偏好系数处理风险项，将多目标优化问题转化为单目标优化问题。线性加权法构建含收益和CVaR 的复合目标函数，如式（17）所示。

式中β为一个范围在[0，1]的加权因子，用于实现收益和CVaR 之间的权衡，即风险偏好系数［13］。通过改变参数β可以得到不同的投资方案，构建收益和CVaR 的有效前沿。β越大，表明越看重风险，此类投资商为风险规避型；β越小，表明越看重收益，即希望尽可能地最大化收益。

求解线性加权法构造的多目标模型得到的pareto 前沿分布性、边界最优性较差。即投资商在基于各个投资方案的收益和CVaR（预期收益）作出选择权衡时，不易调控投资方案梯度。

2.5 增广ε-约束法的多目标处理方法

为改善线性加权法构造的多目标组合问题解集的分布性和边界点的值，提出增广ε-约束法构造含风险管理的多目标模型，映射出多目标优化问题的实际pareto 前沿［16］，提供更易调控收益和CVaR 解集梯度的投资方案，以及更优边界点的解集。

增广ε-约束法的思想是以一个次要目标作为约束条件对另外一个主目标进行优化，在一定范围内调整辅助变量ε 的值进行求解。首先，计算出每个目标的取值范围，即本文中收益和CVaR 目标的取值范围如表1所示。

表1 收益与CVaR目标取值范围Tab.1 Profit and CVaR target value range

表1 中的F11和F22均为在单目标下的最大值，即只考虑F1(x)或F2(x)时的最大值，F12为在收益单目标最大的前提下最大化CVaR，F21为在CVaR单目标最大的前提下最大化收益，计算过程如下。

式中D为满足式（4）、（25）—（36）的决策变量x可行域集合。

表1 中每一列的最大值和最小值可以确定每个目标在pareto 前沿的范围。此时选择收益为主目标，CVaR 作为次要目标和约束将其范围划分为p个相等的间隔，结合辅助变量ε 和松弛变量s将多目标优化问题转为单目标优化问题。

式中：l为CVaR 的最小值；p为CVaR 被划分的间隔数；r为CVaR 值的范围；α为一个足够小的数字；s为CVaR对应的非负松弛变量。

3 收益和CVaR 增广ε-约束法的光储充电站多目标容量优化配置模型

3.1 目标函数

见2.5节的式（22）—（24）。

3.2 约束条件

3.2.1 储能系统电量及充放电功率约束

式中：PESS为储能系统所配置的额定功率；ut为0-1变量，值为1 时仅可充电，值为0 时仅可放电。式（28）和式（29）限定了储能系统充放电功率的范围并保证了储能系统不同时进行充放电。

由于在式（28）和（29）中引入了0-1 变量ut，而PESS也是决策变量，导致了非线性约束的出现。因此，采用big-M法［14］解耦式（28）和（29）。

式中M为设定的一个足够大的正数，实现了非线性约束的解耦，此时，约束式（28）—（29）被转换成约束式（30）—（33）。

3.2.2 功率平衡约束

3.2.3 与电网功率交换约束

式中：Pmax为光储充电站与电网交换功率的最大值，ue为0-1变量，值为1时仅可向电网购电，值为0时仅可向电网售电，保证了光储充电站不同时向电网购售电。

3.3 基于熵权-TOPSIS法筛选客观最优解

求解3.1—3.2 节构造的多目标模型得到pareto前沿，投资商可以根据自身对于收益和CVaR 的权衡主观选择决策方案，也可以采用熵权-TOPSIS 法客观的确定决策方案［22-23］。其核心思想是标准化处理收益和CVaR 指标，基于指标数据的信息熵对收益和CVaR 指标客观赋权，量化各解集与正理想解和负理想解的相对距离作为综合评价值。

1）采用极差法对各指标Xij进行标准化处理，以便消除数量级和量纲的影响。

式中：i为解的序号；j为测度指标，即收益或者CVaR 指标；Xij和Yij分别为收益值、CVaR 值和标准化后的收益值、CVaR 值；max(Xij)和min(Xij)分别为收益或者CVaR的最大和最小值。

2）计算各指标Yij的信息熵Ej。

3）计算各指标Yij的权重Wj。

4）构建各指标的加权评价矩阵S。

式中：n为pareto 解集中的解集数，即本文中的p+1；m为指标数，sij=Wj×Yij。

5）根据加权评价矩阵S确定各个指标的正理想解和负理想解。由于收益和CVaR 都属于效益型指标，即越大越好，则：

7）计算综合评价值。

综合评价值Ri最大的解集最优。

4 算例分析

4.1 算例参数

在MATLAB 中调用Gurobi 求解器求解3.1—3.2 中建立的模型。光伏四季典型出力场景概率均为0.25［13］，采用蒙特卡洛抽样得到EV 的充电需求并利用kmeans 将EV 充电需求聚成四类如图2所示。

聚类后4 类充电功率的概率分别为0.238、0.262、0.262、0.238。从时间角度考虑，光储充电站全部采用快速充电桩给EV 提供充电服务，并且假设不会出现排队充电的情况，即EV 到达光储充电站后立即给EV 充电［6］。公交车、私家车、出租车的充电特征指标及参数见参考文献［19］，EV充电功率及电池容量见参考文献［24］。EV 充电电价a、光储充电站向电网购售电电价b、c如图3 所示。光储充电站与电网交换功率最大值200 kW。光伏和储能的参数见参考文献［25-27］，储能电池初始电量为其总容量的50%。在对3 种价格的设定中，EV 充电电价大于购电电价且远远大于售电电价，确保光储充电站尽可能地给EV提供充电服务，而不是将电量卖给电网［6］。

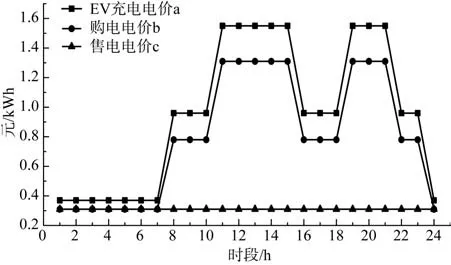
图3 EV充电电价和购售电电价Fig.3 EV charging price and purchase and sale price

4.2 算例结果与分析

4.2.1 增广ε-约束法与线性加权法的比较

现有文献中对含CVaR 风险项的求解问题都采用诸如文献［8］的线性加权法，本文提出增广ε-约束法求解此类问题，为对比两种算法的优劣性，绘制出各自的有效前沿如图4 所示。在传统线性加权法中，置信水平α=0.9，风险偏好系数按0.05 的值递增，而在增广ε-约束法中，间隔p=20，则解集数均为21。

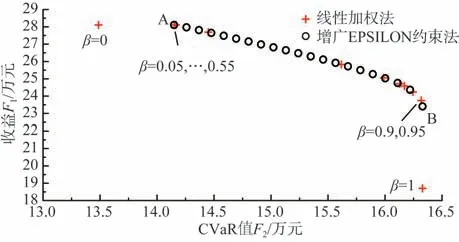
图4 线性加权法和增广ε-约束法有效前沿对比Fig.4 Comparison of effective frontier between linear weighting method and augmented ε-constraint method

在有效前沿上，随着CVaR 值的增大、收益的降低，表明注重CVaR 忽视收益，为风险规避型投资商的投资趋势；随着收益的增大、CVaR 值的降低，表明注重收益忽视CVaR，为效益追逐型投资商的投资趋势。且从线性加权法求得的有效前沿可以看出，均匀分布的权重系数集β并不能保证有效解集{F1，F2}的均匀分布，因此，pareto 有效集合的映射是不充分的，且不同的权重组合会产生相同的有效解，例如：当β=0.9、0.95 或者β=0.05，…，0.55时。因此，可以得知：采用增广ε-约束法求得的pareto 有效前沿的分布性更好，能够提供更易调控收益和CVaR解集梯度的投资方案。

两种方法求得的有效解集是不可比的，因为这两种方法的结果是同一pareto 边界的两种不同映射。但在边界点B、β=1 和A、β=0 是可以比较的，在两者的边界上，方案B 与方案A 分别支配了β=1 和β=0 的方案。对于右下边界，此时相当于相同CVaR，而方案B 相较于β=1的方案具有更高的收益；对于左上边界，此时相当于相同收益，而方案A 相较于β=0 的方案具有更高的CVaR。综上，证明了增广ε-约束法的优越性。

从图4 的pareto 有效前沿可以看出，随着解集中收益的提高，对应的CvaR 值将降低，预期收益可能会低于CVaR 值。这意味着并不存在一个最优解，能够保证收益和CvaR 值同时最大。此时投资商收益的期望值为F1，为各场景收益与其概率乘积之和，而由于光伏出力与电动汽车充电需求的不确定性，实际的收益会出现波动——在一个范围内波动，在90%的置信度预期收益会高于收益的CVaR值，在10%的置信度预期收益会低于收益的CvaR值。图4中的A点对应的收益为281 085元，为投资商收益的期望值为281 085元；CvaR值为141 492元，即在极端市场风险下低收益的平均值为141 492元。

4.2.2 收益和CVaR以及不同容量配置分析

本小节将基于增广ε-约束法所求解集的容量配置进行分析，光伏容量、储能容量功率配置结果如图5所示。

图5 光伏容量和储能容量功率配置结果Fig.5 Photovoltaic capacity and energy storage capacity power configuration results

由于光伏出力和EV 充电需求的不确定性给规划结果带来影响，本文采用场景法处理不确定性后，收益最大的寻优结果实际上是所有场景收益与其概率乘积之和，即一个收益的期望值。而实际上的收益值对应于一个收益分布，为了克服这种模糊性，本文引入的CVaR 能够量化这种收益的波动性，让投资商在投资时能够自主权衡收益和CVaR的关系作出主观决策。

光伏出力和EV 充电需求的不确定性会给各个场景的运行成本带来波动，产生收益波动的风险，并进一步影响光伏储能的容量配置。从图5 可得知：投资商在愈发重视CVaR 进行投资的过程中，会降低对于光伏和储能的容量配置，但是储能对于光伏容量所占比重会提高。降低容量配置能够在一定程度上降低投资维护成本，但是会降低运行收益，由于储能容量的变化不大，这样能够保证通过降低投资而提高的CVaR 值能够比降低投资而降低的运行收益大，即总的CVaR 值能够呈上升趋势。此过程中将增加从电网购电满足EV 的充电需求，并降低光伏容量平抑波动，减少向电网售电。

相反地，投资商在重视收益忽略CVaR 时，会大量投资光伏和储能的容量，虽然提高了投资维护成本，但是保证满足EV 充电需求后减少向电网购电增加向电网售电提高运行收益，且提高的运行成本大于提高的投资维护成本，则总收益提高。但由于投资增大，且光伏波动大，投资商收益的CVaR值将降低，此时实际收益会面临变得很低的情况。

4.2.3 基于熵权-TOPSIS法筛选客观决策方案

首先通过熵权法计算出图4 中增广ε-约束法解集中成本和风险目标的权重：W1=0.546 1、W2=0.453 9。根据TOPSIS 法得出各解集的综合评价值如图6所示。

图6 pareto解集综合评价值Fig.6 Pareto solution set comprehensive evaluation value

图6 中由小到大的解集序号与图4、图5 中CVaR 值从左至右增大的解集一一对应。综合评价值越大表明解集越优，综合评价值最大为0.617 6位于图6 中的第7 个解集，为客观决策方案；对照图5，客观决策方案中各设备容量配置结果为：PPV=265 kW、WESS=352 kWh、PESS=145 kW，收益为271 521 元，为投资商收益的期望值为271 521 元，CVaR 值为148 031 元，即在90%置信水平下收益不低于148 031 元，且在极端市场风险下低收益的平均值为148 031元。

图6中解集6—9综合评价值相近，以客观最优的第7 个解集为基准值，对比解集6、8、9 相对于解集7 的收益和风险变化情况。解集6 的收益提高了0.61%，CVaR 值降低了0.73%；解集8 的收益降低了0.61%，CVaR 值提高了0.74%；解集9 的收益降低了1.23%，CVaR 值提高了1.47%。因此客观最优解集7 是对于成本（收益）和风险给投资商提供的一种客观最优解。若是对于收益或者CVaR值有自己主观倾向意愿的投资商，则可根据收益或者风险的变化情况自主选择其他方案。效益追逐型投资商愿意将效益收益高的方案视为最优方案，风险规避型投资商愿意将CVaR 值高的方案视为最优方案。

4.2.4 客观决策方案与典型方案运行结果对比

在实际投资中，按照投资商的主观意愿，有仅以成本或风险单目标最小的两种典型方案，图6 中的第1个解集和第21个解集分别代表这两种典型方案。第1 个解集的投资结果为：PPV=315 kW、WESS=354 kWh、PESS=146 kW，收益281 085 元，CVaR 值为141 492 元，第21 个解集的投资结果为：PPV=112 kW、WESS=272 kWh、PESS=112 kW，收益234 071 元，CVaR 值为163 290 元。本文共16个场景，仿真结果中各方案第13 个场景的成本均超过了风险值。第13 个场景光伏出力及EV 充电需求如图7 所示，该场景下客观决策方案、仅考虑收益的投资方案、仅考虑CVaR 的投资方案的运行情况如图8、图9、图10所示。

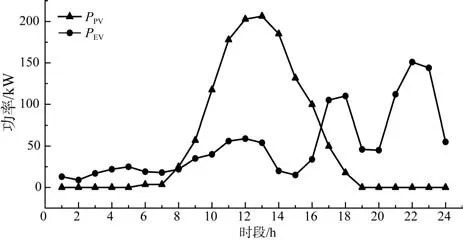
图7 第13个场景的光伏出力及EV充电需求Fig.7 Photovoltaic output and EV charging demand in the 13th scenario

图8 客观决策方案中第13个场景的运行情况Fig.8 Operation scheme of the 13th scenario in the optimal investment scheme

图9 仅考虑收益的投资方案中第13个场景的运行情况Fig.9 Operation of scenario 13 in the investment scheme considering only profits

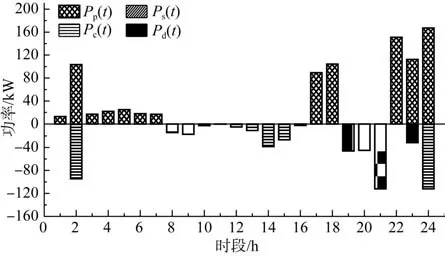
图10 仅考虑CVaR的投资方案中第13个场景的运行情况Fig.10 Operation of scenario 13 in the investment scheme considering CVaR only

由于仅考虑CVaR 的投资方案过度规避风险，光伏和储能的容量配置远远低于客观决策方案以及仅考虑收益的投资方案的容量配置，从图8 和图9、图10的对比中可看出：在仅考虑CVaR 的投资方案中，由于配置的光伏和储能的容量很低。当光伏发电能力很弱时（01：00—07：00时段），该方案只能通过向电网购电来满足EV 的充电需求。当光伏发电能力很强时（11：00—15：00时段），该方案不仅不能向电网卖电获得收益，而且只能存储少量电能。因此，该方案过度的保守投资虽然提高了CVaR 值，但是极大地降低了收益。

客观决策方案相较于仅考虑收益的投资方案：光伏容量配置降低，储能容量基本不变。客观决策方案降低了光伏容量配置，从图8 和图9 的对比可看出，客观决策方案减少了对电网的售电量，虽然降低了运行收益，但是降低光伏容量而降低了投资成本。客观决策方案相比于只考虑收益的投资方案在仅降低3.4%的收益的前提下，CVaR 值提高了4.6%；最优投资方案相比于只考虑CVaR 值的投资方案在仅降低9.3%的CVaR 值的前提下，收益提高了16.0%。

综上，应用本文的模型和方法研究规划问题时需注意以下事项。

1）为投资商度量不确定性给收益带来的风险，需要将收益项放入CVaR 的损失函数部分，并结合虚拟变量求得收益的CVaR 值。同理，也可以拓展到研究成本的CVaR值。

2）建立含CVaR 风险项的模型时，需要将收益及CVaR 分别作为两个目标，并结合增广ε-约束法求解，通过间隔数来调节参数ε 的大小，达到为不同风险偏好投资商提供相应规划运行方案的效果。

5 结语

度量光伏出力及EV 充电需求的不确定性给光储充电站投资商的收益带来的影响，直观地显示收益与CVaR 值的关系，收益越高，预期收益低于的CVaR 值越小，为不同风险偏好的投资商提供投资及运行方案。

与传统处理风险项的线性加权法相比，采用增广ε-约束法得到的pareto 有效前沿分布更均匀、边界点更优，更细致地划分了不同风险偏好的投资及运行方案，便于投资商对CVaR和收益的把控。

在不同的投资运行方案中，投资商可依据风险偏好主观的选择决策方案；也可以采用熵权-TOPSIS 法综合评价各方案，筛选出客观决策方案，得到收益和CVaR的最优权衡。