STATCOM 和同步调相机响应时间的仿真分析和比较

戴朝波，于弘洋，赵国亮，段方维，杨滢璇

（1.先进输电技术全国重点实验室（国网智能电网研究院有限公司），北京 102209；2.国网辽宁省电力有限公司电力科学研究院，沈阳 110003）

0 引言

电力系统电压稳定问题一直是困扰世界电力学术界的难题之一［1-2］。在特高压直流换相失败、闭锁等故障及其恢复过程中，除有功功率大幅波动之外，直流会从交流电网吞吐大量无功功率，导致直流送、受端近区交流电压大幅快速波动，存在新能源机组大规模无序脱网等运行风险［2-3］。

众所周知，提高电网电压稳定水平的动态无功补偿装置主要有SVC［4］、STATCOM［5-7］和同步调相机［8-9］等。关于这三者的比较已有不少［3，9-22］，但都没有事先约定装置响应时间的定义和相应的计算方法，也就没法实质性比较STATCOM 和同步调相机装置本身的响应时间。

通过各种控制，同步调相机励磁系统输出励磁电压Ef，在转子上得到励磁电流If，再通过磁链耦合，最终在定子侧得到期望的内电势E0［11］。从电路机理上讲，同步调相机输出的无功功率及其响应时间由同步调相机的内电势、机端电压和等值电抗共同决定。STATCOM 补偿无功功率的机理与同步调相机相似，不同之处在于：STATCOM 通过控制和脉宽调制等技术使换流器输出期望的交流电压，相当于同步调相机的内电势；同时，等值电抗通常为STATCOM 连接电抗L，与同步调相机不同，其电感值通常是固定的。

文献［22］对西北新甘青750 kV 送端电网无功补偿措施进行比较研究，结果表明：调相机对电网输电能力的提升效果最好，STATCOM 次之，SVC最差，并归因于调相机输出的无功功率最大，即和装置响应时间关系不大。现阶段，鉴于调相机价格远高于STATCOM，而 SVC 价格略低于STATCOM［12］，并且同步调相机运行维护成本和有功功率损耗是三者中最高的，SVC 是最低的，因此，宜对电网有相似电压支撑效果的方案进行比较，而不是对装置相同额定容量的方案比较。

早期，普遍认为STATCOM 响应速度比同步调相机快［20-22］，或同样快［11］。文献［3］基于定子绕组磁链不能突变，认为同步调相机能无延时地输出超出其额定容量的无功功率。工程现场单相短路故障试验结果却表明［23］：同步调相机在10～30 ms 内可提供1.2～1.3 倍额定容量的无功功率，即响应时间不为0。这一显著差异应是对响应时间的不同理解造成的。文献［10］通过机电暂态仿真发现SVC 和STATCOM 呈现无功电压“反调”特性，并归因于这两者响应速度不够快，同时同步调相机能快速发出或吸收无功功率，没有无功电压“反调”现象而被推荐，可见响应速度至少是一项重要技术指标。文献［24］研究了同步调相机接入等值电网后电网电压幅值发生突变时的暂态响应特性，但没有探讨响应时间。没有涉及响应时间的原因在于装置的响应特性受电网条件等诸多因素影响，也在于电网条件发生突变后，仿真得到的无功功率存在幅值较大的高频振荡［3，24］。毕竟在没有约定相关定义和计算方法前提下很难给出有说服力的结果。

本文首先明确阶跃响应时间的定义，并约定相应的计算方法，统一了比较基准。接着分别搭建了简化的、便于验证的同步调相机和STATCOM 等值系统，降低了诸多因素交叉影响的错综复杂性。采用电磁暂态仿真分析方法分别从参考值阶跃、电网等值电压幅值阶跃、相角阶跃这3 个维度试图得到装置本身的响应特性。实际应用时，上述3 个量肯定会同时变化，本文的研究结果将为分析和理解更为复杂的实际工况下的响应时间提供有益参考。

1 仿真比较的约定

1.1 阶跃响应时间

图1 给出阶跃响应时间的示意，约定动态无功补偿装置阶跃响应时间为从阶跃发生时刻开始，到输出达到实际变化值90%为止，且期间没有过冲。这里的实际变化值指图1的稳态值与初始值的差。

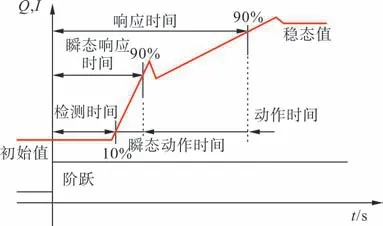
图1 阶跃响应时间示意图Fig.1 Schematic diagram of step response time

实际应用时有采用无功功率Q或输出电流I来表征阶跃响应时间的，本文采用无功功率Q来表征。

如图1 所示，阶跃响应时间包括检测时间和动作时间这两部分。对于STATCOM 等电力电子装置，检测时间和动作时间通常都不为0。

考虑到同步调相机的特殊性，如图1 所示，本文引入瞬态响应时间，相应的实际变化值为局部最大值和初始值的差。

在此约定系统频率不变，并采用快速傅里叶变换、递推离散傅里叶变换（recursive discrete Fourier transform［25］）等措施减少谐波分量、有功分量的影响。本文采用一个工频周波128 点的傅里叶变换计算相应的有功功率、无功功率和基波分量等。

1.2 等值系统

图2 给出STATCOM 和同步调相机响应时间比较时用到的、在PSCAD 软件中搭建的仿真等值系统。P、Q和i分别为动态无功补偿装置输出的有功功率、无功功率和电流，正方向如箭头所示，并约定动态无功补偿装置等效为电容时的无功功率Q为正，等效为电感时Q为负。

图2 比较时采用的等值系统Fig.2 Equivalent system for comparison

以动态无功补偿装置额定值为标幺化基准值，在参数设置时，确保变压器和等值阻抗ZS的参数标幺值在同步调相机和STATCOM 算例中的对应值都是相等的。这样一来，即使同步调相机和STATCOM 额定容量不同，仿真计算结果也同样具有可比性。

按照工程现场相对较弱的交流系统，通过约定的短路比来设置图2 的等值阻抗，这样处理的目的在于：在适当考虑电网特性的前提下，尽可能地聚焦于装置本身，使比较结果更能体现装置自身的性能。

动态无功补偿装置的参考值阶跃、等值电源的幅值阶跃、等值电源的相角阶跃是本文比较装置阶跃响应时间的3 个维度。其中，参考值阶跃时的特性属于装置的主动响应特性，等值电源的幅值和相角阶跃时的特性则属于装置的被动响应特性。

现有电力行业标准［26］规定STATCOM 正常运行最低工作电压应为0.4 p.u.，在韩国投运的400 Mvar STATCOM 最低工作电压为0.3 p.u.［5］。实际电网不一定都要求这样严格，有时0.6 p.u.最低工作电压也是可以接受的［6］。本文选用0.5 p.u.最低工作电压较为适中的要求进行比较。如电压跌落幅度太小，同步调相机需要高压侧电压附加励磁控制［22］等辅助调节来优化响应特性。当然，电压跌落速度慢会增加动态无功补偿装置的响应时间。本文选用阶跃响应，即瞬时改变以确保同步调相机能呈现出尽可能小的响应时间。

已有研究结果表明［27］，在电网发生故障的整个过程中，电压有可能发生大到90 °的相角跃变。同时考虑到，如分布式调相机一样，STATCOM 也应能应用到新能源基地等场景，所以，本文也选用90 °相角跃变进行比较。

2 同步调相机的仿真和分析

2.1 仿真条件的说明

图3 给出了仿真分析时同步调相机的等值系统，其中Vref为同步调相机端电压参考值，Ef为励磁电压，If为励磁电流。尽管有研究结果表明同步调相机在频率为5.0 Hz以上区间的响应特性基本上与励磁控制策略无关［9］，在仿真等值系统搭建时还是考虑了励磁系统及其参数的影响。

图3 同步调相机的等值系统Fig.3 Equivalent system with a synchronous condenser

仿真时用到的同步调相机参数按上海电气额定容量为50 MVA 的空冷调相机进行设置，其中，额定定子线电压为10.5 kV，额定定子电流为2 749 A，额定转速为3 000 r/min。

当同步调相机并网以后，通常采用调节速度快、可控性强的自并励静止励磁系统［8］。本仿真采用IEEE的ST5静止励磁系统模型及其参数值［28-29］。

变压器额定容量为75 MVA，采用△/Y0接线，变比为10.5 kV/500.0 kV，基波正序漏抗为0.12 p.u.。电网的等值阻抗为一电感，按调相机额定参数进行标幺化，对应值约为0.0261 p.u.。

2.2 仿真分析

2.2.1 机端电压参考值的阶跃

图4给出了同步调相机端电压参考值Vref的阶跃响应曲线。无功功率Q从0 p.u.上升到1.0 p.u.时的响应时间约为0.854 s。显然，励磁电压Ef上升速度相对较快，但励磁电流If变化速度要慢许多，最终导致端电压参考值的阶跃响应时间较长，这和文献［3］中相关论述相符。尽管通过优化励磁系统及其参数可以缩短阶跃响应时间，但很难改变阶跃响应时间至少为数百毫秒的这一判断。

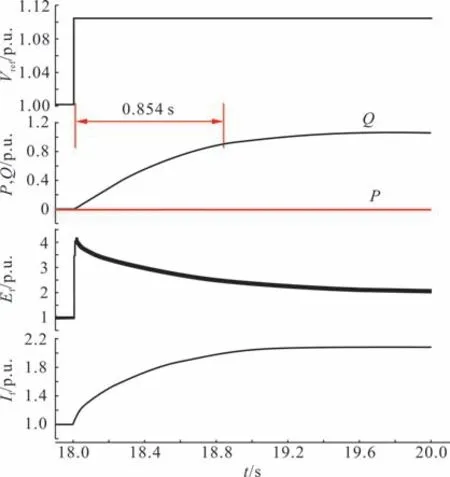
图4 电压参考值的阶跃响应曲线Fig.4 Step response waveforms of voltage reference

2.2.2 等值电源电压幅值的跃变

图5 给出图3 中等值电源幅值Vs的阶跃响应曲线。在18.0 s 时刻，幅值Vs由1.0 p.u.瞬间跌到0.5 p.u.，相应地，VH由1.0 p.u.跌到0.56 p.u.，V由1.0 p.u.跌到0.75 p.u.，VH和V的下降幅度都有所减少，这是由于受到等值阻抗Zs和变压器漏抗的影响。由于同步调相机无功功率Q缓慢增加，VH和V也都随之增加一些，且V增加的幅度更为显著。

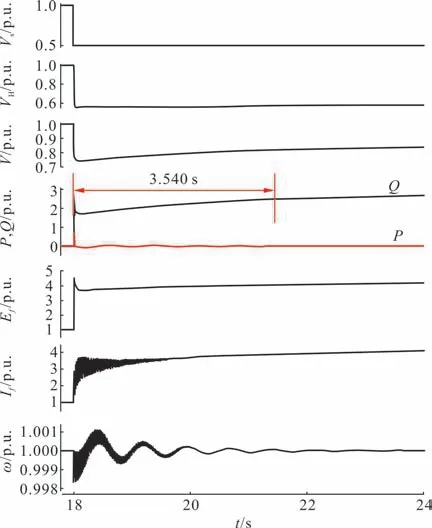
图5 电压幅值的阶跃响应曲线Fig.5 Step response waveforms of voltage amplitude

如图5 所示，采用Q稳态值时，电压幅值的阶跃响应时间约为3.540 s，比较大，这主要是因为无功功率Q的增速在后期比较缓慢。通过增加高压侧电压附加励磁控制［22］、优化励磁系统及其参数值等措施，应能缩短响应时间，但很难改变阶跃响应时间在1.0 s 以上的这一判断。文献［24］给出了系统电压突然跌落到0.6 p.u.时的无功功率响应曲线，其阶跃响应时间大约为2.0 s，大于1.0 s。

如图5 所示，等值电源幅值Vs阶跃时，励磁电压Ef和励磁电流If都有幅值较大的跃变，不同的是励磁电流If有频率相对较高的振荡分量，同步调相机励磁绕组的等值电阻不大是该振荡分量持续时间较长的主要原因。同步调相机转子角速度ω峰峰值变化范围仅为额定转速的0.3%左右，可忽略。

如图6 所示，对于瞬态响应时间，从等值电源幅值VS阶跃发生时刻到无功功率Q达到局部最大值的0.9 大致需要14 ms，阶跃响应速度非常快。显然，电流i几乎是无延时地突增，并含有数值较大、缓慢衰减的直流分量。如此大的直流分量至少对升压变压器是不利的。如电流i幅值不变且没有直流分量的话，达到局部最大值的0.9 最快也需要18 ms。I1ave是电流i三相基波分量的平均值，其值在快速上升到最大值后略有下降，其实，电流i幅值是一直在变化的，在等值电源电压幅值Vs阶跃时，其大小通常由同步机超瞬态参数所主导，之后逐渐过渡到由瞬态参数所主导，因此电流i幅值应该是衰减的，这是瞬态阶跃响应时间能小于18 ms 的原因之一。另外一个原因是电流中含有衰减的直流分量。

图6 电压幅值的阶跃响应曲线Fig.6 Step response waveforms of voltage amplitude

与文献［3］、［24］不同，由于采用了1.1 节中约定的计算方法，图5 和图6 中Q才没有高频振荡的分量，也就能相对容易地确定阶跃响应时间。

如图6 所示，无功功率Q达到1.2 p.u.的时间约为10.6 ms，达到1.3 p.u.的时间约为11.06 ms，确实让同步调相机呈现出较快的响应特性。这和文献［23］中“同步调相机在10～30 ms 内可提供1.2～1.3 倍额定容量的无功功率”的结论是相符的。50 MVA 同步调相机的仿真分析结果能和300 MVA 同步调相机的现场试验结论相符，从一个侧面反映出本文所采用的仿真模型及其仿真结果是能反映实际设备的响应特性，具有一定的代表性。

2.2.3 等值电源电压相角的跃变

图7 给出了图3 中等值电源相角θ的阶跃响应曲线。在18.0 s 时刻，VS相角瞬间跃变90 °，由于同步调相机具有机械惯性，再加上励磁系统的调节作用，使得同步调相机输出呈现幅值较大的振荡，这些振荡对电网电压暂态控制显然是不利的。a 相电压有效值VHa、Va和励磁电压Ef都有比较明显的大幅振荡，VHa振荡的最大峰峰值为0.235 p.u.，Va振荡幅度比VHa的还要略大些，这是因为电压的振荡是由同步调相机及其励磁系统的调整引起的；有功功率P也出现幅值较大的振荡，振荡的峰峰值最高达8.12 p.u.，相应的振荡持续时间长达1.5 s；无功功率Q振荡的最大幅值达3.0 p.u.，相应的振荡持续时间大约为20 ms；转子角速度ω的振荡频率有两个，频率较低的和有功功率P的振荡频率相近，频率较高的和励磁电压Ef、励磁电流If中高频振荡的振荡频率相近。

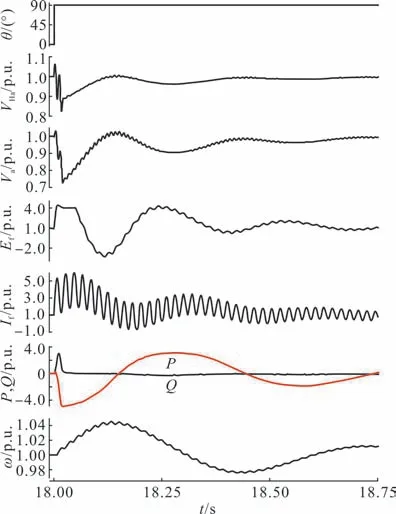
图7 电压相角的阶跃响应曲线Fig.7 Step response waveforms of voltage phase angle

有功功率的振荡体现出同步调相机具有正的整步功率系数特性，但这一特性也带来电压幅值的振荡，对电网暂态电压稳定来说，这应该是不利的。

3 STATCOM的仿真和分析

3.1 仿真条件的说明

图8 给出了仿真分析时STATCOM 的等值系统。按闽粤联网背靠背直流输电工程来设置相应的等值阻抗、变压器、STATCOM 主电路及其参数。

图8 STATCOM 的等值系统Fig.8 Equivalent system of STATCOM

STATCOM 三相额定容量为± 120 Mvar，每相换流链由16 个H 桥功率模块串联而成，其中，1 个功率模块是冗余的。换流链采用星形接法，中性点直接接地，并通过升压变压器接入500 kV 电网。功率模块直流电压的期望值为2.1 kV，功率模块直流电容额定容值为10 mF。功率模块的开关频率为275 Hz，采用单极倍频PWM 调制方式，通过载波移相使整个换流链等效的开关频率为8.8 kHz。升压变压器采用Y0/Y0接法，变比为500 kV/ 35 kV，额定容量为180 MVA，基波正序漏抗为12.0 %。连接电抗L额定电感值为2.0 mH。按直流输电额定容量的短路比为2.3 来设置电网的等值阻抗，即按照相对较弱的交流系统来设置。

STATCOM 确实可以采用类似电网构造（grid forming）型［30］的控制策略，从而获得不一样的阶跃响应时间，但是，现有工程中应用的STATCOM 几乎都是采用电网跟随（grid following）型的。鉴于此，本文也选用电网跟随型策略。

当电网电压在正常范围内时，STATCOM 通常采用无功控制和电压控制这两种模式；当超出约定范围时，STATCOM 通常采用电流控制模式，即输出允许的最大容性或感性电流［6］。STATCOM 采用分相控制策略，从而具有较强的电网不对称运行能力。分相瞬时电流控制由单相锁相环、无功电流参考值、有功电流参考值、瞬时电流控制等4 个部分组成，并采用准比例谐振（quasi-proportional resonant，QPR）控制实现对瞬时电流参考值的无静差跟踪，详见文献［6］。

3.2 仿真分析

如无特殊说明，仅给出a 相波形。vdcMax、vdcMin、vdcAve分别为STATCOM 的a 相16 个级联H 桥功率模块直流电压中的最大值、最小值和平均值。

3.2.1 无功电流参考值的阶跃

图9 给出了STATCOM 无功电流参考值Iqref在1.0 s 时刻从0 p.u.阶跃到1.0 p.u.容性的仿真波形。仿真结果显示阶跃响应时间约为19.2 ms，比理想值18 ms 仅慢了1.2 ms，这是因为：a）STATCOM 输出电流跟踪参考电流大约需要1.0～2.0 ms 时间［3］，这可以从电流i波形曲线可以看出；b）由于电流的快速跟踪需要换流器输出电压的剧烈变化，从而导致电压v波形产生畸变，使无功功率值变小，即阶跃响应时间变长。毫无疑问，与图4仿真结果相比较，STATCOM 参考值阶跃响应时间要小许多。

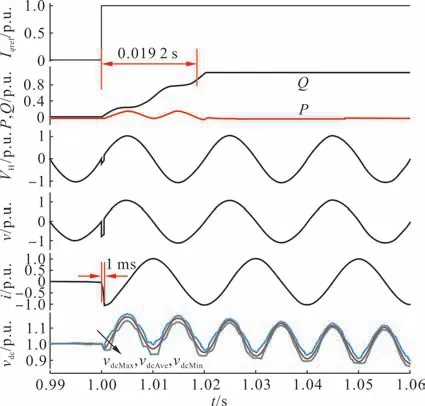
图9 无功电流参考值的阶跃响应曲线Fig.9 Step response waveforms of reactive current reference

此外，vdcMax、vdcMin和vdcAve波形都没有出现振荡发散和越过限值等现象，说明H 桥直流电压的均压和稳压控制都能正常工作。

3.2.2 等值电源电压幅值跃变

图10给出图8中等值电源幅值Vs的阶跃响应曲线。在1.0 s 时刻，幅值Vs由1.0 p.u.瞬间跌到0.5 p.u.，相应地，VH由1.0 p.u.跌到0.534 p.u.。与图5 的同步调相机结果相比，下跌得更多，这是由于STATCOM 过载能力相对较弱，所提供的无功功率较小造成的。电压幅值的阶跃响应时间约为22.6 ms，比同步调相机图5 的3.540 s（稳态值的对应值）要小许多，但比同步调相机图6 的14 ms（瞬态响应时间的对应值）略大些。除在3.2.1 中提到的输出电流跟踪参考电流需要1.0 ms～2.0 ms 时间之外，参考电流Iqref本身也有相应的响应时间，即图10 中所示的4.7 ms。这是因为在实际工程中，通常采用电网电压有效值进行判断［6］，尽管VH能瞬时突降，有效值VH变化则要慢不少。

图10 电压幅值的阶跃响应曲线Fig.10 Step response waveforms of voltage amplitude

在此需要补充的是，与同步调相机图6 结果相比，可以认为图10 输出电流ia是没有直流分量的，这对升压变压器是有利的。

文献［31］采用电流来表征STATCOM 响应时间，大小为15.8 ms，换算成用无功功率来表征响应时间，大小约为31.7 ms。比本文前面的22.6 ms还要大些的原因有两个，一是文献［31］中STATCOM 对电流指令的上升率做了限制，二是控制器的延时略大。文献［31］代表了2012 年STATCOM 的技术水平。当前，数字信号处理器的处理能力和处理速度比2012 年都有大幅提升，控制器延时能大幅减小。正如本仿真算例所示，控制策略改进让STATCOM 不再需要对电流指令上升率等进行限制。总之，按照现有技术水平，STATCOM 应能达到本仿真算例的响应时间。

如采用电网电压瞬时值进行判断，且约定相应的判断延时为0.5 ms 时，图11 给出对应的等值电源电压幅值阶跃响应曲线。无功电流参考值Iqref上升时间显著减少，从而使电压幅值的阶跃响应时间由之前的22.6 ms 减小到20.2 ms，不过，仍然比同步调相机图6 的14 ms（瞬态响应时间的对应值）要略大些。同样，电流的快速变化也带来电压vHa和va波形畸变的问题。

图11 电压幅值的阶跃响应曲线Fig.11 Step response waveforms of voltage amplitude

3.2.3 等值电源电压相角跃变

图12 给出图8 中等值电源vs相角θ的阶跃响应曲线。在1.0 s 时刻，VS相角θ瞬间跃变90 °，a相电压vHa和va波形有明显突变，a相电压有效值VHa也有明显波动，相应波动的峰峰值达0.161 p.u.，但比图7同步调相机VHa的0.235 p.u.还是要小些。与图7 结果相比较，STATCOM 有功功率和无功功率的波动完全可以忽略不计。图12中ω是STATCOM锁相环估计出的角速度，最大值达1.243 p.u.，比图7 同步调相机转子角速度的最大值1.045 p.u.要大不少。可见，尽管STATCOM 锁相环估计的频率也是剧烈变化的，但由于STATCOM 无功电流参考值Iqref没有随之剧烈变化，输出的有功功率和无功功率也就没有剧烈变化。从无功功率补偿的角度，这是有利电网暂态电压稳定的。

图12 电压相角的阶跃响应曲线Fig.12 Step response waveforms of voltage phase angle

4 同步调相机和STATCOM的比较和分析

表1 总结同步调相机和STATCOM 的比较结果。

表1 同步调相机和STATCOM 的比较Tab.1 Comparison between the synchronous condenser and the STATCOM

对于参考值阶跃，同步调相机端电压参考值Vref阶跃响应时间至少为数百毫秒。STATCOM 无功电流参考值阶跃响应时间仅为19.2 ms，明显优于同步调相机。

对于电网电压幅值由1.0 p.u.瞬时跌到0.5 p.u.这一工况，按稳态值计算时，受励磁系统响应速度慢的不利影响，同步调相机阶跃时间要大许多，基本上都在1.0 s 以上，引入瞬态响应时间这一新概念后，同步调相机瞬态阶跃响应时间约为14 ms，确实比较小。采用有效值进行电网电压跃变判断时，STATCOM 响应时间大致为22.6 ms，改为电压瞬时值进行判断时，响应时间大致能做到20 ms 左右，仍比同步调相机瞬态阶跃时间要大6.0 ms 左右。如再充分利用装置的过载能力，让STATCOM 输出电流在电压瞬时跌落后的半个工频周波内略大些，计算得到的响应时间还能再小些。

对于电网电压相角阶跃，同步调相机出现幅度较大的振荡，对电网电压暂态控制应该是不利的，与之相反，STATCOM 有功功率、无功功率等几乎没有变化，有利于电网电压暂态稳定。

5 结语

本文约定阶跃响应时间的定义及其计算方法，统一了比较基准并消除了高频振荡等不利影响。通过简化的、便于验证的等值系统降低实际应用中诸多因素交叉影响的错综复杂性，并从参考值阶跃、等值电源的幅值阶跃和相角阶跃这3 个维度较为详细地比较了同步调相机和STATCOM 装置自身的阶跃响应特性。结果表明：同步调相机仅在电网电压幅值阶跃时，瞬态响应时间才略优于STATCOM。