基于集成聚类及改进马尔科夫链模型的光伏功率短期预测

李一，杨茂，苏欣

（现代电力系统仿真控制与绿色电能新技术教育部重点实验室（东北电力大学），吉林 吉林 132012）

0 引言

受到复杂、变化多端的气象因素影响，光伏电站的有效功率输出具有强烈的波动性和不确定性，光伏发电系统并网后可能会影响电力系统的发电计划及检修机组等任务［1-3］，光伏出力曲线的预测对调度部门与未来发电规划具有重要意义。

明确功率序列各分量特征有助于提高功率预测效果，文献［4］阐明了光伏功率序列可分解为多种频率分量，分别代表受不同气象因素影响而产生的功率分量，但并未考虑实际物理意义［5-6］，实现高低频序列进一步合并，增加计算成本的同时，无法解决间断信号数据的存在会导致单一本征模态分量（intrinsic mode function，IMF）中包含多种频率分量［7-10］，不符合IMF 的定义。文献［11］将光伏功率曲线进行分解预测，提出不同特征分量分别建模预测，在考虑突变天气的影响下，引入白噪声辅助分解，但这些噪声并未滤除，在后续预测中可能增加预测误差，降低模型预测的准确性。

光伏日出力曲线受气象因素影响会出现多种类型，划分出全年可能出现的趋势序列一定程度上能够减小预测误差，文献［12］针对光伏出力的特点，使用K-means 算法距离公式选择欧式距离，从大量原始数据集中划分不同特征的出力序列，但每次预测得到的聚类中心并不固定［13］，无法确定聚类初始中心，同时可能会出现波动剧烈但幅值较大的序列与光伏出力曲线平缓幅值较小的序列划入同一聚类簇中，直接影响该出力类型的模型建立及预测效果。文献［14］阐明了马尔科夫链模型具有很好的预测效果，但对于区间划分没有考虑状态转移矩阵的特点［15-20］，当日出力最值未处于某一区间端点时，状态转移概率矩阵无法控制两种相反的变化，导致模型预测精度下降。文献中针对马尔科夫链模型出现平稳分布及训练集数据存在常返态的情况并未做出假设与解决办法。预测模型可以提取有效特征作为模型的输入［21-22］，同时也可以作为模型改进的依据［23］，但未考虑模型输入特征量的增加对计算成本及预测精度的影响。

在以上方法研究的基础上，提出通过集成聚类划分得到物理意义明确的两个分量，即趋势序列与随机序列，避免因分解后各分量分别建模导致误差积累及噪声引入造成影响［24］。集成聚类方法既保证处理大数据集的高效性，同时避免单一聚类方法结果不唯一［25-27］。根据马尔科夫链模型的优势，考虑其建模特点，在传统模型基础上使用一阶差分提取趋势序列波动变化特征［28-30］，并以此为依据划分特征时段，各区间分别建模预测，防止因进入平稳分布导致预测不收敛，同时充分发挥状态转移矩阵控制单一变化速率的优势［31-32］。本文利用光伏电站实际运行数据进行建模来验证所提模型的有效性以及不同地理位置条件下的适用性。

1 预测模型原理

1.1 划分聚类及层次聚类集成算法

受辐照度、湿度等气象条件因素的影响，光伏电站日出力曲线整体趋势各不相同。处于相似天气情况下的功率输出差值更小，利用聚类算法筛选与待预测日功率曲线趋势相似、数值接近的聚类中心作为典型代表可以提升后续模型的预测精度［12］。典型聚类算法包括密度聚类、层次聚类、网格聚类、划分聚类以及基于模型的聚类方法。单一聚类方法难以实现既保证聚类效果又能确定聚类个数，针对大量数据，单一方法的聚类精度与聚类效率无法同时兼顾，并且不能判断最优聚类数量。

通过分析传统聚类算法的优缺点，结合层次聚类的高精度与划分聚类的高效性，本文提出一种集成聚类算法。使用划分聚类K-means 算法将历史功率数据集进行初步聚类获得样本簇聚类中心，在此基础上将得到的聚类中心继续做层次聚类，划分聚类代替层次聚类处理大量数据提高效率，节省了层次聚类需要计算的样本间距离矩阵的存储空间。本文选择戴维森保丁指数（Davies-Bouldin index，DBI）和轮廓系数（silhouette coefficient）来确定最优聚类个数，公式如式（1）—（3）表示。

式中：avg为簇内样本间平均距离；n为样本个数；m为样本维数；xit、xjt为样本点；DBI为戴维森堡丁指数；k为聚类个数；Ci、Cj为样本簇；ci、cj为样本簇聚类中心；S(i)为轮廓系数；b(i)为簇外样本间距离；a(i)为簇内样本间距离；i、j为变量序数的下标；t为变量维数下标。

1.2 改进马尔科夫链模型

马尔科夫链（Markov chain，MC）是一种能反映事件对象离散状态间变化过程的数学模型，具有无后效性，即待预测时刻的状态仅由其相邻前一时刻所处状态决定，与其他时刻无关。光伏功率序列可视作一种不同状态间的转移过程，马尔科夫链模型可以通过建立状态转移概率矩阵预测功率变化趋势及待预测时刻功率值处于不同状态区间的概率。

马尔科夫链模型单步预测结果为功率预测值处于各状态区间内的概率值，多组状态区间使用列向量PN表示，如式（4）所示。

式中：PN为各状态区间概率列向量；P(xN)为处于对应状态区间的概率；n为状态区间数量；N为预测序数。

模型用于预测曲线变化的状态转移矩阵为方阵，阶数等于状态数量，矩阵第N行元素代表由状态xN向其他状态转移的概率值（包括转移至状态本身），转移概率矩阵P如式（5）所示。

式中PN1为矩阵元素，物理意义为状态xN向状态x1转移的概率。

单独转移概率矩阵中元素值Pij的分母为元素所在行数，即转移前状态出现的总次数；分子为由状态i变为状态j的频数。待预测值或状态PN+1根据式（6）来确定。

状态转移概率矩阵可以有效地跟踪序列的变化趋势、引导数据转移方向，并控制预测值增减速率。传统马尔科夫链模型有一定的局限性，在出现曲线变化速率突变、数值波动剧烈的情况下，单一状态转移矩阵无法应对预测过程中出现的复杂变化。当数据出现常返态，即数值多次经历同一状态区间，MC模型将进入平稳分布导致预测无法进行，而数据波动的存在成为出现平稳分布的充分条件。状态转移概率矩阵对预测效果有直接影响，矩阵元素由状态区间划分决定，区间间隔过大会导致单步预测值难以估计；区间间隔太小容易导致矩阵变为稀疏矩阵，增加矩阵维数降低预测效率。一般情况下，单独转移概率矩阵只能反映序列的一种变化，那么提取待预测序列有效变化特征，并以此为依据划分预测区间可以提升模型精度。对光伏日出力曲线进行一阶差分处理，结果如图1所示。

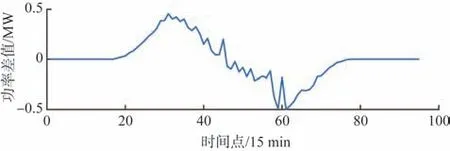
图1 光伏日功率曲线一阶差分值Fig.1 First order difference values of PV daily power curve

由图1 可知，光伏功率曲线在上升及下降时段的变化速率并不恒定，单独状态转移矩阵无法达到预测目标，根据上文分析，使用多个表达不同变化趋势的状态转移概率矩阵代替原始矩阵可以提升预测效果，不同矩阵分别对应预测过程中某一变化速率。一阶差分值既能反映数据波动，也可以体现序列变化情况，针对马尔科夫链模型单步预测的特点，在预测前对训练集数据做一阶差分处理，得到能够体现原始序列变化速率及相邻两点间增减关系的数据。根据一阶差分值划分的各区间分别对应一个特征时段，为防止矩阵维数向极端发展，同一特征时间段为连续且变化速度接近的序列。

1.3 差分整合移动平均自回归模型

随机序列为光伏实际功率序列与趋势序列的差值，代表光伏电站出力受云层移动、降雨等天气因素影响产生的高频率短时波动。根据其频率高、幅值小等特点，使用ARIMA（autoregressive integrated moving average model）模型对随机序列进行预测，模型可表示为式（7）。

式中：L为滞后算子；d为差分阶数；p为自回归阶数；q为移动平均阶数；Φi为自适应系数；θi为移动平均系数；εt为残差序列；Xt为待计算变量。

差分整合移动平均自回归模型的步骤如下：1）选择ADF 方法做单位根检验判断随机序列的平稳性，当滞后算子多项式未出现单位根时，待预测序列为平稳的；反之，为非平稳。对非平稳随机序列做d次一阶差分处理直到检验为平稳序列为止，d即差分阶数；2）求取自相关函数与偏自相关函数，通过赤池信息准则判断AIC 最小值来确定模型的阶数q和p；3）模型的参数通过最小二乘法得到，使用残差白噪声检验及参数的显著性检验来判断参数；4）使用ARIMA模型预测随机序列。

2 模型建立及预测流程

光伏发电日功率曲线在趋势上呈现一条类抛物线，受环境与气象因素影响在该抛物线的基础上再附加一些波动。本文数据来自吉林省某光伏电站实际数据。在预测开始之前对数据集进行检验，保证同一电站功率及NWP（numerical weather prediction）数据在不同时段的通用性。

2.1 集成聚类划分趋势与随机序列

首先使用划分聚类K-means 算法将光伏功率样本集分成多个样本簇，再利用层次聚类将数值和趋势接近的聚类中心聚合得到新的聚类簇，集成聚类算法从原始功率数据集中提取出所有光伏出力类型曲线并以各聚类簇的聚类中心作为趋势序列，最终聚类个数通过DBI 指数与轮廓系数来确定，其中DBI 指数表征聚类簇内距离与其他簇间距离的关系，值越小聚类效果越好；轮廓系数为正表示样本聚类合格，结果值越大效果越好。各聚类中心分别代表不同发电情况下的光伏出力类型。

不同聚类方法得到的随机序列数值概率分布情况如图2 所示。从图中可以看出，作为划分趋势序列与随机序列的方法，集成聚类的随机序列数值拟合曲线处于0 值及其附近值较小区间的概率更高，表明集成聚类较划分聚类能更好地将体现整体变化情况的数据保留在趋势序列中。聚类算法本身无法确定划分的最终个数，引用DBI指数与轮廓系数确定最优聚类样本簇数量，DBI 指数值如图3 所示。由图可知，集成聚类的DBI指数要低于其他聚类方法，说明其聚类效果更好并且当聚类个数为5 时，DBI 指数达到最低，此时轮廓系数为0.426 8，因此最优聚类个数为5 个，本文划分出5 种光伏出力类型，即趋势序列。

图2 不同聚类方法下的随机序列数值分布Fig.2 Numerical distribution of random sequences under different clustering methods

图3 不同聚类算法DBI指数Fig.3 Comparison of DBI index of different clustering algorithms

2.2 预测模型的建立

使用改进MC 模型预测趋势序列，可以有效避免序列存在波动导致MC 模型进入平稳分布。通过皮尔逊相关系数选择NWP 中与功率序列相关性较高的气象数据来确定待预测日的出力类型和波动数据。单独状态转移概率矩阵预测单一增减变化趋势的效果最优，如果按固定时段划分预测区间，大概率会出现变化情况差异较大的两个时间段被归进一个预测区间中，同时也可能将待预测序列幅值所在时点未划至区间端点，使该区间出现两种完全相反的变化趋势，直接导致此时间段准确率下降甚至预测不收敛。由于前一区间的最后预测数值为相邻下一区间的初始值，且马尔科夫链模型具有无后效性，导致预测精度不高的数值介入其他预测区间，形成恶性循环，降低整体预测准确率。光伏发电日出力在一天内呈现两种相反的变化趋势，全天的特征时段划分至少以正午时刻为分界点划为两段，在此基础上通过一阶差分处理挖掘待预测时间段的序列特征进一步划分特征时段。

图4 为趋势序列改进MC 模型与传统MC 模型预测对比散点图，点集越靠近等值线预测精度越高，5 种序列可视为不同季节及天气下的光伏出力类型。由图可知，改进MC 模型预测结果更接近实际值，相比于直接固定时段划分方法，特征时段的划分不仅提升了预测精度和预测效率，也降低了计算成本。随机序列由ARIMA 模型预测得出结果，同趋势序列预测结果相加得到最终预测值。

图4 划分特征时段模型与传统模型对比散点图Fig.4 Scatter diagram comparing the model of dividing characteristic period with the traditional model

改进MC模型预测框架图如图5所示。

图5 预测框架图Fig.5 Forecasting frame diagram

3 算例分析

3.1 数据来源与评价指标

本文数据选用吉林省某光伏电站2017—2018年实际光伏发电运行数据及NWP 数据。选取电站中某一场站进行单场预测，时间分辨率为15 min，装机容量为20 MW。清除功率序列异常数据，以2017 年1 月1 日至12 月31 日全年数据作为训练集，2018年1月1日至12月31日数据作为测试集，检验本文提出模型的可行性，选择传统MC-ARIMA 模型、改进MC 模型、传统MC 模型以及LSTM 长短时记忆网络作为对比模型。

本文衡量模型预测效果的评价指标为均方根误差（root mean square error，RMSE）、平均绝对误差（mean absolute error，MAE）、平均绝对百分比误差（mean absolute percentage error，MAPE）和均方误差（mean square error，MSE），计算公式如分别如式（8）—（10）所示。

式中：n为样本数据数量；PPi为i时刻实际功率；PMi为i时刻预测功率；Cap为装机容量。

3.2 集成聚类划分趋势与随机序列

集成聚类算法首先使用K-means 算法进行初步划分，本文初步聚类样本簇数量设定为20；其次，层次聚类进一步合并上一步得到的聚类中心，样本间距离度量计算公式选择欧氏距离，聚类结果如2.1 节所示，5 种趋势序列包含的样本数量分布如图6所示。

图6 各趋势序列样本数分布情况Fig.6 Distribution of sample number of each trend series

根据饼状图分布情况及NWP 数据分析，趋势序列a 所在样本簇为数值波动较为剧烈的集合，占比很小，包含雨天等天气类型；序列b 代表夏季多云天气电站出力情况；序列c 为晴天发电状态；序列d 为春秋两季类晴天出力类型；序列e 代表阴天天气下的发电状态，该状态在全年中占比最大。

3.3 改进MC-ARIMA模型预测结果

以待预测日NWP 数据为依据选择对应的趋势序列以及随机序列进行建模。根据皮尔逊相关系数选取与光伏功率序列相关性较高的短波辐射、温度及相对湿度为主要依据。

以趋势序列b 为例，将趋势序列进行一阶差分处理，结果如图7 所示，开机时光伏功率上升速率较慢；在10：00 功率增速最大；接近幅值时增速开始下降，下午光伏功率曲线变化趋势与上午相反，根据一阶差分值将序列划分为6 个特征时段分别建模预测。全天共96 个时点，无光照时间段不参与预测过程，其中第一段时点区间为［19，28］；第二段为［28，38］；第三段为［38，45］；第四段为［45，54］；第五段为［54，65］；第六段为［65，77］，第45时点出现序列最大功率值。

图7 趋势序列b一阶差分值Fig.7 Trend series b first order difference value

划分特征时段后，各区间根据功率数值规定状态区间，每一段的初始功率值为上一段预测值，初始值的状态转移计入转移概率矩阵中，区间最后功率的状态转移由下一矩阵承接，不计入当前特征时段中，趋势序列b 预测结果对比如图8 所示。从对比图中可以看出，本文方法模型相比于传统MC 模型预测效果更好，预测曲线变化速率以及数值更接近实际出力曲线。由于不需要直接固定划分大量时段，减少大量计算成本，同时也防止因固定划分使曲线幅值未处于区间端点，导致预测精度下降。提取随机序列，通过ARIMA 模型得到预测结果，与趋势序列预测曲线相叠加得到最终预测曲线，所有出力类型预测结果如图9—13所示。

图8 趋势序列b预测对比Fig.8 Comparison of trend series b predication values

图9 趋势序列a出力类型Fig.9 Trend series a output type

图10 趋势序列b出力类型Fig.10 Trend series b output type

图11 趋势序列c出力类型Fig.11 Trend series c output type

图12 趋势序列d出力类型Fig.12 Trend series d output type

图13 趋势序列e出力类型Fig.13 Trend series e output type

从所有出力类型图可以看出，本文所提模型预测曲线整体趋势上更接近实际功率曲线，当待预测曲线出现小幅值的波动时预测效果更好；波动较剧烈时，本文所提方法预测曲线更靠近实际出力曲线，在非晴天天气类型下对比模型误差快速增大，但本文模型均方根误差、绝度误差等指标均保持最小，在不同出力类型下准确率相比其他模型更高一些。根据各类型待预测日NWP 数据可知，晴天天气类型下各模型预测效果差距不大，当待预测日出现了云层遮挡及降雨天气情况，本文提出的模型在阴天天气类型下预测数值并未过分偏离实际出力值，预测精度高于其他对比模型。

为进一步说明模型预测精度，选取一天中出力类型不唯一，即出现多种天气类型的日出力序列作为待预测日，预测结果如图14 所示。由图可知，在雨转晴天的天气情况下，本文模型的预测更加灵活，相较于对比模型预测曲线更接近实际曲线，可以更准确地预测一天中出现多种光伏出力类型序列。

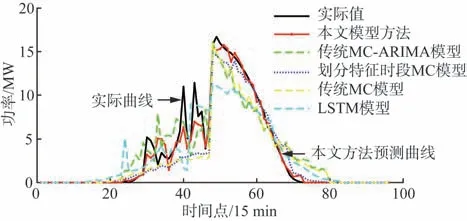
图14 混合出力类型Fig.14 Mixed output type

各误差评价指标雷达图如图15所示，所有可能出现的出力类型准确率最低为89.18%，最高为97.71%，均高于传统MC模型在内的其他模型，说明本文所提模型在不同季节和天气情况下具有较高的准确率。其中，趋势b 类型的待预测日下午出现了较大波动，RMSE 值为0.052 3，略高于类型a。类型d 的RMSE 值与MAE 值等误差指标均为最高，表明本文所提模型由于气象因素影响产生序列波动越剧烈，误差越大，准确率较高的类型a误差最低，其MAE值为0.015 1，MSE值为0.394 2。代表突变天气的趋势d 类型，本文所提模型MAE 值为0.050 4，对比模型MAE值最低为0.058 5，对比模型预测误差均高于本文预测方法。综上所述，本文模型在气象条件恶劣条件预测效果更好，在所有天气类型及多种出力类型下准确率均为最高且误差最小。

图15 各种出力类型评价指标Fig.15 Evaluation indexes of various output types

该光伏电站2018 年全年发电短期预测评价指标平均值如表1 所示，本文模型准确率高于其他对比模型，全年平均值为92.63%，各误差指标均为最小，其中相比于传统MC 模型的RMSE 值减小了0.084 4，MAE 值降低了0.038 3，相较于LSTM 模型准确率提高了6.99%。改进后的MC 模型相比传统模型在误差上有所减小，其中MSE 值减小了2.169 4，说明改进MC 模型可以有效减小各时刻预测值与实际值的偏差。本文所提模型误差要低于单独改进MC 模型，结合前文各趋势序列预测结果加以分析，表明MC 模型针对波动频数较大的情况，预测效果较差，而配合ARIMA 模型分别预测趋势与随机序列能大大提高准确率。同传统MCARIMA 模型相比，本文模型准确率提高了1.76%，说明改进MC 模型能更好地预测趋势序列，进而在整体上减小预测误差。

表1 吉林省电站评价指标平均值Tab.1 Average value of evaluation index of Jilin power station

3.4 模型的适用性

为体现本文模型的适用性，选择气象因素差异大、经纬度及地理位置等相差较远的青海省某光伏电站的数据进行预测。该电站装机容量为40 MW，使用数据为2018 年至2019 年光伏功率及对应的NWP 数据，其中2018 年作为训练集；2019 年为测试集，全年各项评价指标平均值如表2 所示。可以看出，本文模型针对天气变化情况较为复杂的地区准确率仍然满足短期功率预测要求，且误差较小，该模型对不同地区、不同光伏输出类型具有一定的适用性。

表2 青海省电站评价指标平均值Tab.2 Average value of evaluation index of Qinghai power station

4 结论

为解决光伏功率具有随机性等特点及传统马尔科夫链模型难以预测功率序列波动较大的问题，结合划分聚类处理数据的高效性与层次聚类抗干扰性的优点，提出通过集成聚类提取聚类中心作为光伏功率曲线的趋势序列，将代表波动的随机序列幅值降到最小。利用一阶差分处理得到序列变化趋势来划分特征时段以改进马尔科夫链模型，使用改进MC 模型预测趋势序列，防止因出现常返态进入平稳分布导致预测停止收敛；在保证预测精度的同时，减小计算成本。根据ARIMA 模型的特点，使用该模型预测随机序列。

对吉林省光伏电站进行建模预测，本文所提预测模型全年平均准确率为92.63%，高于其他对比模型。模型预测值的年平均RMSE 值比传统马尔科夫链模型减少1.76%，相较于LSTM 模型下降6.99%，MAE 和MSE 误差值均为最小。通过对青海省光伏电站建模预测，本文所提模型全年平均准确率为90.14%，相比于传统MC 模型提高了7.07%，证明本文模型针对不同地区、不同气象类型具有适用性。

本文模型主要聚焦于功率数据的处理与应用，预测针对NWP 数据的使用较少。后续工作将在引入气象数据来提升预测方法的精度，同时在空间相关性层面进行研究，完善预测模型的不足。