基于无迹变换法的电力系统小扰动稳定概率分析

陈将宏，徐彬，何长民

（三峡大学电气与新能源学院，湖北 宜昌 443002）

0 引言

在电力系统中，小扰动稳定是一项重要指标，它能够体现电力系统在经受小扰动后能否继续同步运转。常规小扰动稳定分析以系统在某一确定运行点处的线性化模型和特征值分析法为基础，属于确定性分析范畴［1-3］。但在实际电力系统中，大多数系统输入变量具有随机性，而部分变量具有相关性。常规的确定性分析难以把系统小扰动稳定进行全面的分析。因此，需要针对不确定因素进行概率性分析，得到小干扰稳定评估指标。

将概率方法引入电力系统稳定性分析是Burchett 在1977 年提出的［4］，小扰动稳定概率分析的重点是根据输入随机参数的分布，确定系统振荡模式的分布特征，进而计算出如下数据：随机输出变量（如特征值均值、标准差），用于确保电力系统对小扰动的稳定性。目前，小扰动稳定分析方法有：蒙特卡罗法［5］、点估计法［6-7］、随机响应面法［8-9］等。其中，蒙特卡罗法计算量大、所需时间长，主要运用于算法检验，在本文中用于与提出的无迹变换法作对比。点估计法是通过已知输入变量样本估计整体的方法。随机响应面法适用范围较窄，需要先将非正态分布输入变量进行转化，使其服从标准正态分布再进行分析。

无迹变换法［10］是英国学者Julier 提出的，用于解决非线性变换问题，该方法只需已知样本的均值及协方差，即可有效处理随机变量。根据现有文献，该方法已应用于解决概率潮流及概率最优潮流［11-16］、电压稳定［17］等方面的问题，且得到优良的效果，但在小扰动稳定方面的研究较为缺乏。基于无迹变换法的适用条件较广泛、精度较高的特点，可以得出该方法在小扰动稳定的概率分析中适应性较强的结果。

针对现有研究的不足，本文提出一种基于无迹变换法的电力系统小扰动稳定概率分析方法。首先根据各负荷节点注入有功功率的均值及协方差，采样得到Sigma样本点，再通过仿真筛选出系统振荡模式的特征值。最后，根据各个Sigma 采样点的不同权重大小，得到系统振荡模式特征值的均值和标准差，结合小扰动稳定评估指标对小扰动稳定进行分析。

1 随机因素的概率模型

通过非线性方程组刻画的电力系统为：

式中：t为时间；x为状态变量，表征系统中元件的动态特性；z为代数变量；p为参数变量，如有功功率的注入等。

在平衡点（x0，z0）将方程组（1）进行线性化得到：

消去代数变量得到：

式中：A为系统状态矩阵；依据李雅普诺夫第一法［18］，系统在经受小扰动后稳定的条件是：A中特征值实部不为零或者是正数。

本文考虑的是负荷水平的随机性，而由于实际系统的检测误差，负荷有功功率参数预测有偏差。文献［6，19］考虑有功负荷服从正态分布，分别通过点估计和概率分配法，对电力系统小扰动稳定进行概率分析，验证了该方法的准确性和有效性。文献［20］将安全域方法应用于含风电的电力系统小扰动稳定的概率分析，计及了有功负荷服从正态分布，结果表明所提方法能有效减少小扰动稳定概率分析的计算负担。

因此有功负荷在仿真计算中作为随机变量，近似认为服从正态分布，则可以得到负荷概率密度函数为：

式中：Pd为负荷有功功率；μ为负荷期望；σ为标准差。

2 基于无迹变换法的小扰动稳定概率分析

2.1 无迹变换法的基本思路

已知输入变量x在计算后得到均值μx及协方差Cxx，按照特定的采样规则选择一组Sigma 样本点。然后对每个样本点进行非线性变换得到y，最后对求得的小扰动稳定指标集{yi}加权，计算出输出变量y的均值μy和协方差Cyy。基本原理如图1所示。

图1 无迹变换基本原理Fig.1 Basic principle of unscented transformation

无迹变换法的求解步骤如下。

1）若x为k维变量，则均值μx为k维列向量，协方差Cxx为k阶方阵。使用特定的采样策略所得到的输入变量的Sigma样本点集为：

式中：χi为Sigma样本点集；N为样本点数量。

2）对所有Sigma 样本点集{χi}的每种采样状态，进行非线性变换fUT(·)，得到{yi}。

3）根据权重分配，非线性变换后得到的点集{yi}，在加权计算后得到输出变量y的均值和协方差分别为：

2.2 无迹变换法的采样策略

无迹变换法的采样策略在整个算法中十分关键，各种采样策略的使用会取得不同输出样本点集的数量和权重，适当的采样策略可以有效地提高计算效率和精度。现有文献提到的样本点采样策略有：对称采样、最小偏度单形采样、超球体单形采样等。相比之下，对称采样的样本点分布均匀，在小扰动稳定概率分析中性能和精度较好，因此采用对称采样。此外，本文需要求解的是特征根的均值和协方差等参数，要求采样后能全面涵盖样本集的效果明显，采用的是低阶采样策略。

本文根据文献［10］引入比例信息参数α以及高阶信息参数β，经过上述的采样，可以得到的样本点{χi}为：

式中：α为比例参数；W0为均值处Sigma 点的权重系数；Cxx(i)为矩阵中k维向量的第i个元素。

由式（10）可以看出，2k+1 个Sigma 样本点的权重系数满足只要改变W0的值，就能改变各Sigma采样点到均值点的间距。

式中：β为高阶信息参数；若没有根据文献引入高阶信息参数β，则

2.3 基于无迹变换法的小扰动稳定概率分析步骤

本文使用无迹变换法分析电力系统小扰动稳定，振荡模式的特征值表示为电力系统中随机输入变量x的函数，其中x为系统中各负荷节点的注入有功功率。则基于无迹变换法的小扰动稳定概率分析的步骤如图2所示。

图2 基于无迹变换法的小扰动稳定概率分析步骤Fig.2 Steps of probability analysis of small disturbance stability based on unscented transformation method

可以看出通过较少的计算可得到待求特征值的均值、标准差等统计信息。相较于蒙特卡罗等算法，计算量和仿真时间上有显著减少。

3 基于无迹变换法的小扰动稳定仿真

3.1 节点有功负荷的抽取

根据上述模型中有功负荷服从正态分布，可以设某一结点j的注入有功功率Pj服从均值μj及标准差σj的正态分布。采用文献［21］近似逆变换法，在［0，1］之间生成均匀分布的随机数序列R，通过计算得出标准正态分布随机变量Xj。具体步骤如下。

1）正态密度分布曲线下的面积Q(m)，其对应的m可由式（13）计算得到。

其中Q可由式（16）得到。

2）标准正态分布随机数X表示为：

因此，某一节点j的注入有功功率Pj表示为：

式中Xj为标准正态分布随机变量。

考虑其他元件参数也可以使其服从正态分布，采用式（18）进行计算。

3.2 小扰动稳定评估指标

系统状态矩阵中，特征值λi对应第i个模式，则在小扰动稳定性分析中，各个模式由不同的特征值决定。对于实数特征值，一个负实数特征值表示系统稳定，而正实数表示非周期性不稳定。其中负实数特征值体现的是振荡模式的衰减速度，绝对值越大，说明速度越快［22-23］。

对于复数特征值，一对复数特征值是一对共扼值，代表了一个振荡模式。特征值的实部对系统振荡的阻尼比影响较大，虚部能计算出系统的振荡频率。

式中：λ为一对复数共轭特征值；ω为振荡的角频率；η为特征值实部，η＞0 表示增幅振荡，η＜0表示衰减振荡；f为振荡频率；ξ为阻尼比，当0 ＜ξ＜0.03 时，对应弱阻尼振荡模式，当ξ＞0.03时，系统小扰动稳定且具有较好的阻尼特性。因此，由计算可以得出以下小扰动稳定评估指标。

1）系统特征值的均值、标准差等。可根据详细问题，例如本文考虑的是遭受微小扰动后的稳定性，则选取部分特征值（如低频振荡模式特征值等）的数字特征。

2）其他派生指标。由系统特征值可计算阻尼比均值的系统特征参数。

4 算例分析

本文采用美国西部联合电力系统IEEE 3 机9 节点的系统作为分析算例，利用MATLAB中PSAT软件进行小扰动稳定性的概率分析。系统接线图如图3所示。

图3 3机9节点系统接线图Fig.3 Diagram of a 3-generator 9-bus system

从图3中可以看出，该系统包含3台发电机、9个节点和3 个负荷节点。其中，3 台同步发电机使用的模型都是经典四阶模型，发电机G1 设为平衡节点，G2 和G3 的发电机为PV 节点。设基准容量100 MVA，频率为60 Hz。在PSAT［24-25］中进行所有仿真。

4.1 无迹变换法的计算精度

本文考虑的随机变量分别是母线5、6、8 上的有功负荷P5、P6和P8。计及负荷功率波动时，设P5、P6和P8相互独立。假设IEEE 3 机9 节点标准算例中各负荷节点的注入有功功率参数作为均值，10% 的均值作为标准差，即P5～N(1，0.12)，P6～N(0.9，0.092)，P8～N(1.25，0.1252)。

本文参照文献［8］设定采样的权重W0=0.5，比例信息参数α=0.2、高阶信息参数β=0.8。为测试本文方法的有效性，采用蒙特卡罗模拟法，通过2 000次仿真，对所得结果进行比较验证［26］。计算得到的特征值均值和标准差，分别定义其相对误差为：

式中：εμ、εσ分别为特征值均值和标准差的相对误差；μUT、σUT分别为无迹变换方法得到的均值和标准差；μMC、σMC分别为蒙特卡罗模拟方法得到的均值和标准差。

4.2 算例1：考虑两个随机变量

针对母线5、8上的有功负荷P5、P8，采用无迹变换法和蒙特卡罗模拟法计算得到结果，并进行对比分析。根据MATLAB 仿真可知，共有3 个振荡模式，表1 给出了两种算法分析得到的特征值均值及相对误差，表2 为两种算法分析得到的特征值标准差及相对误差。

表1 考虑两个变量的特征值均值及相对误差Tab.1 Mean eigenvalues and relative errors of considering two variables

表2 考虑两个变量的特征值标准差及相对误差Tab.2 Standard deviation and relative error of the eigenvalues of considering two variables

由表1—2 可以看出，与蒙特卡罗模拟法相比较，采用无迹变换法得到的特征值均值及标准差的最大相对误差小于3%，可满足工程应用需要。

4.3 算例2：考虑3个随机变量

针对母线5、6、8 上的有功负荷P5、P6和P8，采用无迹变换法和蒙特卡罗模拟法计算得到结果，并进行对比分析。表3 给出了两种算法分析得到的特征值均值及相对误差，表4 为两种算法分析得到的特征值标准差及相对误差。图4 给出了表中结果相对应的图形对比。

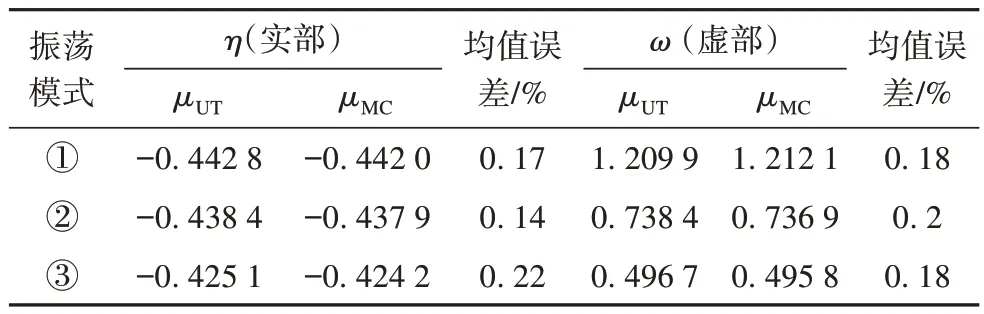
表3 考虑3个变量的特征值均值及相对误差Tab.3 Mean eigenvalues and relative errors of considering three variables

表4 考虑3个变量的特征值标准差及相对误差Tab.4 Standard deviation and relative error of the eigenvalues of considering three variables

图4 算例1、2均值及标准差的相对误差Fig.4 Relative errors of mean and standard deviation of examples 1 and 2

从图4 可以看出，随着随机输入变量数量的增加，均值及标准差的相对误差也不断提高，证明了变量的增加对算法的结果有一定的影响。但采用无迹变换算法得到的特征值后，两种算法均值的相对误差小于1.2%，标准差相对误差小于3%，计算精度较好。

由小扰动评估指标可以计算出各个模式的阻尼比均值，图5 给出了两种算法计算得到的阻尼比均值对比。分析图5 可以得出，两种算法得到的阻尼比均值相差很小，证明了无迹变换法在小扰动稳定概率分析时计算精度较好。对于振荡模式1，阻尼比均值为0.343 69，最相关机组为G1；对于振荡模式2，阻尼比均值为0.510 52，最相关机组为G1和G2；对于振荡模式3，阻尼比均值为0.650 22，最相关机组为G3。阻尼比均值越大，说明该振荡模式衰减越强、稳定性越强。根据小扰动稳定指标中ξ的取值，ξ均大于0.03，说明该系统具备良好的阻尼特性。

图5 两种算法阻尼比均值对比Fig.5 Mean damping ratios comparison of the two algorithms

表5 分别给出了两个算例采用无迹变换法和蒙特卡洛法的仿真时间。从表5 可以看出2 000 次蒙特卡罗模拟法所用时间远超无迹变换法，这是因为在刻画电力系统中考虑k个变量，只需2k+1 次小扰动稳定分析，即可得到系统振荡模式特征值的均值和标准差。所以运行速度和效率远高于蒙特卡罗法，因此无迹变换法更有效地实现了电力系统小扰动稳定的概率分析。

表5 两种算法的仿真时间对比Tab.5 Simulation time comparison of the two algorithms

4.4 New England 39节点系统算例

新英格兰系统包括10 台发电机、39 个节点、12 个变压器和34 条线路，代表美国新英格兰州的一个345 kV 电力网络。10 机39 节点系统的电气接线图如图6所示。

图6 New England 39节点系统Fig.6 New England 10-generator 39-bus system

基于MATLAB中的PSAT软件仿真计算，建立New England 10机39节点模型，进行小扰动稳定分析。系统基准容量为100 MVA，基准电压为345 kV。图7 给出了该系统z域小扰动稳定性的特征值分析结果。

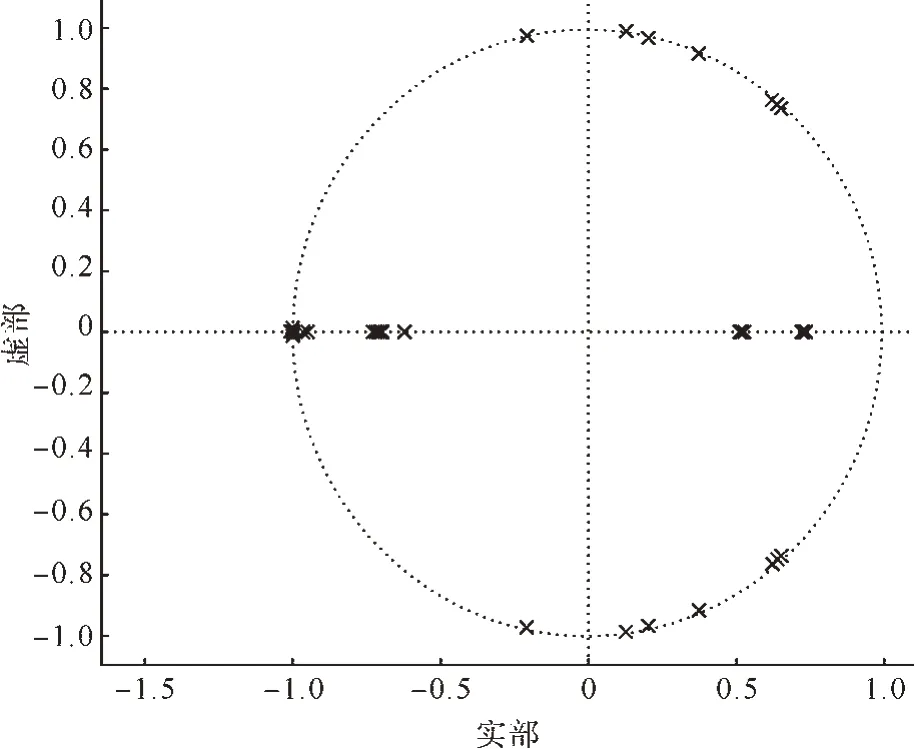
图7 系统z域的小扰动稳定性特征值分析Fig.7 Eigenvalue analysis of small distribution stability in z domain of system

从图7 中可以看出，在z域分析中，所有的特征值都不在单位圆外，说明所有模式对系统的小扰动稳定性不产生影响，因此New England10机 39节点系统能够保持小扰动稳定。

分别使用无迹变换法和两点估计法［27］对该系统进行小扰动稳定概率分析。为考虑整个电网的小扰动稳定性，本文考虑的随机变量分别是母线20、25、29 和39 上的有功负荷P20、P25、P29和P39。表6给出了低频振荡模式的特征值统计数据。

表6 特征值统计数据Tab.6 Statistics of eigenvalues

对表6 分析可得，无迹变换法与两点估计法结果相差很小，证明无迹变换法计算结果准确可靠。从表6可以看出，振荡模式1和2的阻尼比均值远远大于0.03，说明小扰动稳定性较强。而振荡模式3、4和5的阻尼比均值都较小，小扰动稳定性较弱。

其中，振荡模式5 的阻尼比均值小于0.03，属于弱阻尼，应该在其最相关机组G3 处安装PSS，用于提高该振荡模式的阻尼比均值。

5 结语

本文采用无迹变换法进行电力系统小扰动稳定概率分析，在MATLAB 中电力系统分析软件包PSAT 的IEEE3 机9 节点系统进行仿真，得到系统振荡模式特征值的均值和标准差，分析了负荷水平对系统小扰动稳定的影响。通过无迹变换与蒙特卡洛算法之间的对比，验证了无迹变换法的有效性。

最后针对新英格兰10 机39 节点进行仿真和实践，通过无迹变换和两点估计算法的对比，证明了本方法具备分析负荷水平不确定性对小扰动稳定影响的功能。本文所提方法只需要根据随机参数的均值和协方差信息，即可得到小扰动稳定概率分析的重要指标如特征值、阻尼比均值等的统计特性。本文使用的方法类似于黑箱分析，相比于传统的蒙特卡洛法，计算精度和实用性较强。此外，该方法可以直接用于基于确定性分析下的小扰动稳定概率分析。