基于“画计算”作品的“分数除以整数”算法辨析
文|陈 昱(特级教师) 王 芳
“分数除法”历来是小学数学的重点学习内容,其算理理解也是小学生常见的学习难点。其实除了算理理解基础上的算法掌握,计算学习过程具有更深邃的育人意义。
一、“分数除以整数”算法梳理
本文涉及的“画计算”作品数据来自某县城小学六年级两个班的课堂生成,在任务一的学习中,针对“÷2 到底是怎么算出结果的?”这个问题,90 位学生主要有五种不同表现(如表1)。表现一只交代了计算结果,没有呈现计算的思维过程,表现五其实是综合了表现三和表现四的算法。
表1 ÷2 算法梳理
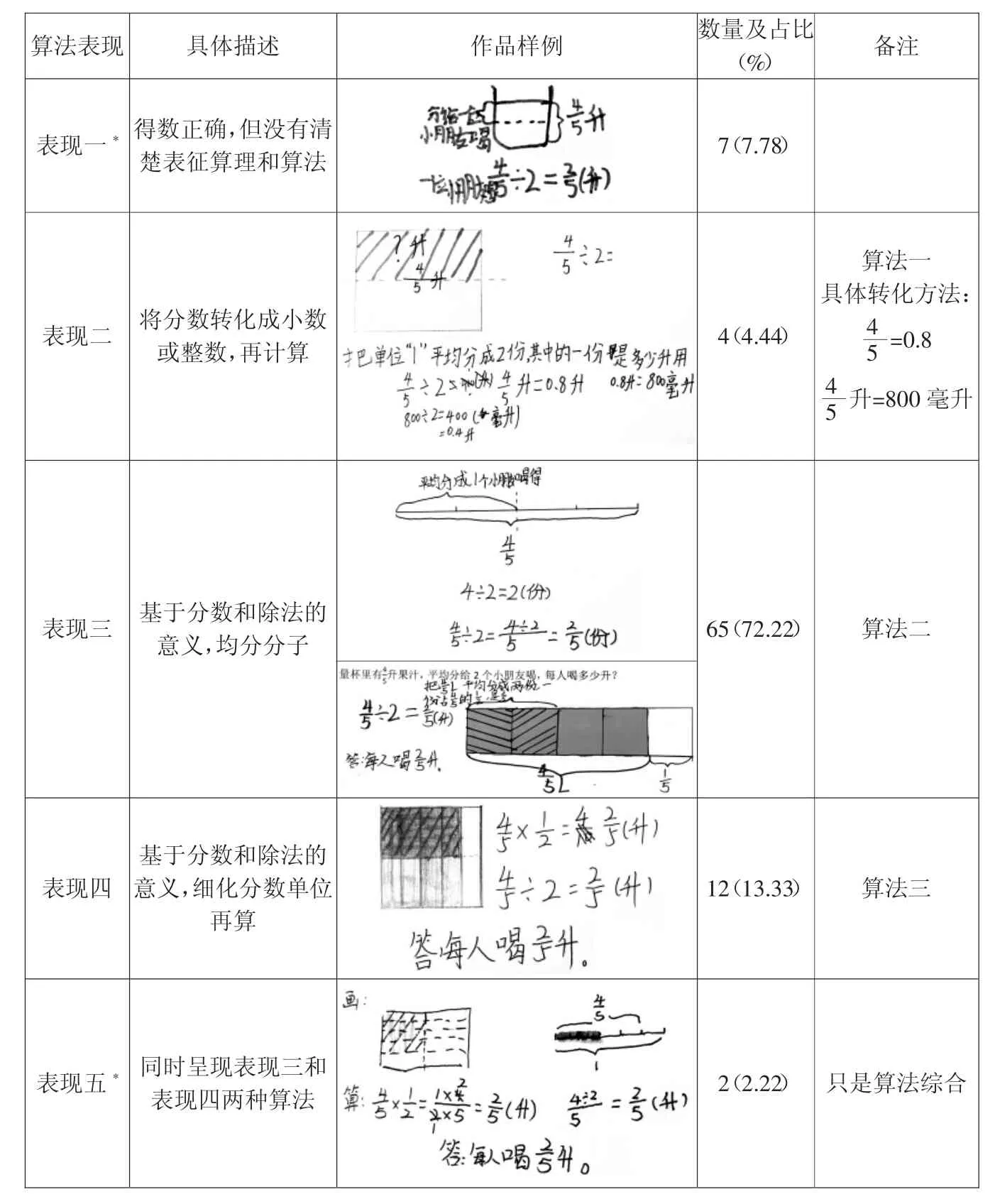
表1 ÷2 算法梳理
算法表现具体描述作品样例数量及占比(%)备注images/BZ_30_1443_1598_1718_1768.png表现一* 得数正确,但没有清楚表征算理和算法7(7.78)images/BZ_30_1336_1797_1832_2105.png表现二 将分数转化成小数或整数,再计算4(4.44)算法一具体转化方法:4 5 =0.8 4 5 升=800 毫升images/BZ_30_1404_2136_1758_2399.png表现三 基于分数和除法的意义,均分分子65(72.22)算法二images/BZ_30_1330_2418_1830_2598.png表现四基于分数和除法的意义,细化分数单位再算images/BZ_30_1385_2611_1786_2851.png12(13.33)算法三images/BZ_30_1334_2874_1825_3135.png表现五* 同时呈现表现三和表现四两种算法2(2.22) 只是算法综合
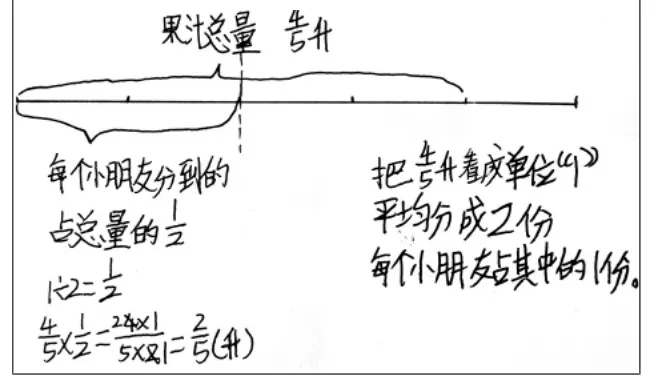
图1
因为任务一的展评环节淡化了算法一,着重引导学生聚焦算法二和算法三,所以到任务二探究÷3 时,呈现出来的算法比较集中,要么循着算法二的思路,要么采用算法三的做法,结果上看,除了未探究成功的,最后都走向了算法三。
探究活动最顺利的是一开始就选择用算法三来计算的学生,很快就得出正确结果(如图2)。选择算法二的学生无一例外都走了弯路,但突破困难终获成功的体验也是很有价值的(如图3、4),探究失败的错例主要就发生在这一环节。

图2
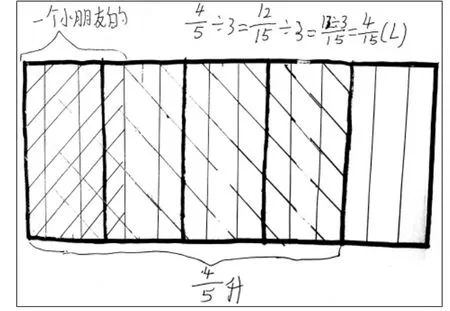
图3
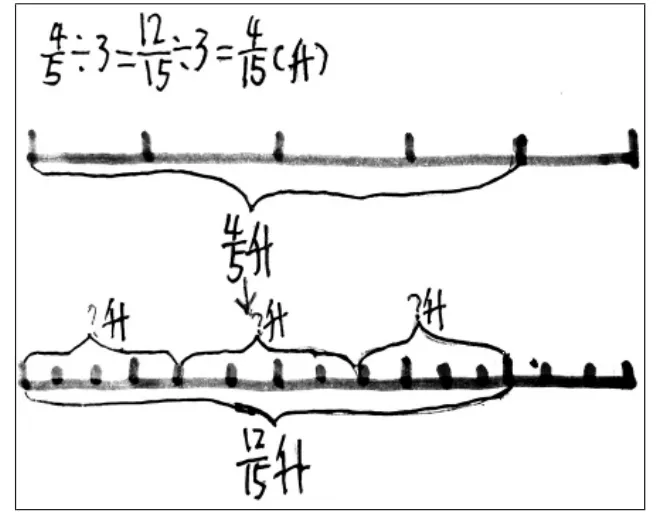
图4
二、“分数除以整数”算法辨析
1.算法探究:两种策略与逻辑
转化是一种重要的数学思想方法,算法一的学生就是将不会算的÷2 转化成会算的0.8÷2 或800÷2,从而解决了问题。本问题的这种转化算法,很快就遭到学生的反思性质疑:所有的分数都可以转化成小数吗?(转化没问题,只不过不一定都是有限小数,也不一定都是循环小数)转化后好算吗?(遇到无限小数,确实不好算,如果除数是分数就更不好算了)……
其实算法一更大的弊端是不利于计算领域的创新发展,即不利于探索出分数除法的专用法则。所以只能采用第二种策略,直面问题。要想探索分数除法的计算,必须先理解分数和除法的意义,即从问题的本质出发探求解决之道。这也是一切运算的共同逻辑,基于运算对象和运算本身的意义。
2.分数领域:两种视角与路径
当学生直面问题,不再回避不会算的分数除法,往往会发现别有洞天。在分数除以整数运算里,不同学生基于两种不同视角产生两种不同路径:直接均分分子或先扩充分母再算。
学生能想到直接均分分子的方法,得益于数据特征,即分子4能被2 整除,4 个分数单位很容易被平均分成2 份;改为均分成3份就有困难了,需要先细化分数计数单位。
细化计数单位,在计算中不是第一次遇到,在整数和小数除法里是常见的现象与策略。这种策略一般在计算遇到困难时用起来更自然,即在÷3 时运用要比在÷2 时运用更能凸显其价值,但这并不代表后者不能运用。很多学生会用表1 中表现四的作品样例呈现的这种算法来计算÷2,但鲜有学生自觉意识到此法是先将分数的计数单位细化成,算的其实是,即便有感觉也不强烈;而在的计算过程中就能比较明显地感受到,先细化分数单位为。
3.算法辨析:普适与本质
基于以上算法二和算法三,通过观察、交流与归纳,学生可以初步建立分数除以整数的两种算法模型:b、c 为自然数,b、c≠0,a 能被c 整除)和(a、b、c为自然数,b、c ≠0)。可以看出:(1)模型一中分数的分数单位一直是,模型二中分数的分数单位细化成了;(2)模型一中分数的分子需要能被作为除数的整数整除,也就是限定了条件。
于是问题来了,算法二和算法三在分数除以整数计算中分别具有怎样的地位?笔者认为算法三更具普适性,而算法二更本质。
首先,算法三适用于所有的分数除以整数的计算,算法二只适用于分数的分子能被整数整除时,属于特殊情况,因此算法三更具一般性和普适性。
其次,从分数和除法的意义出发,除法作为乘法(求几个相同加数的和的简便运算)的逆运算,其基础是平均分,所以算法二更为本质。分数除以整数,就是将分数单位的个数平均分。算法三在细分分数单位后,又回到算法二,即算法三包含算法二。或者说,由算法三建立的算法模型的完整形态是这样的:(a、b、c 为自然数,b、c≠0)。
基于以上分析,我们可以说:分数除以整数,有时候可以直接除,有时候需要细化分数单位后才能除,后者适用于所有的情况。
这种算法分析还可以继续向整数除以分数、分数除以分数延伸,只不过情况要复杂得多。
三、“分数除以整数”教育启示
以上基于“画计算”作品的“分数除以整数”的算法辨析,可以给予我们多方面带有哲学意味的教育启示。
1.关于问题解决策略
(1)转化问题可以低成本较快捷地解决问题,但是也往往会错过创新机会。
(2)直面问题可能成本较高,但更有利于创新发展,面对新情况,开创新局面,困难总是与机遇并存。
(3)创新问题解决的关键在于回归问题本原,把握知识本质,本质性意味着生长性,越本质越有力。
(4)具体问题具体分析,针对不同问题,灵活选择相适应的解决策略与方法。
2.关于问题解决方法
(1)视角不同,路径不同。视角不同来自个性差异,每一位学生都是独一无二的存在,所以在学习与问题解决方法上,参差多态乃幸福之源。
(2)适合的就是最好的。所谓算法优化、最佳解等往往基于多样比较后的个性化选择,有自己想法很重要,理解他人也很重要,内在想法与对外理解都是发展变化的,所以这个“合适”和“最优”也是动态变化的。
(3)万法通融。世界是广泛联系的整体,不同事物在本质上是统一的,不同方法在本质上是相通的,联系的眼光可以洞穿世界的真相,帮助我们通往灵活不拘的自由境界。
(4)辨析是认识之道。世界是整体的,也是可分的;是千差万别的,也是通融的……辨析才能认识其本质与变化。
立德树人是教育的根本目的,数学育人是数学教育的永恒追求,计算育人要求我们通过具体的计算教学活动给予学生计算学习之内和计算学习之外的各种有益滋养。如果学生能从“分数除以整数”课堂上收获以上知识技能、经验方法、包括运算能力在内的学科核心素养,以及诸多哲思启蒙,那么将在尽可能大的范围内实现计算的育人价值。
——辨析“凌乱、混乱、胡乱、忙乱”

