解密神奇的“缩小空间”——例谈“代言画”的教学应用与价值

文|陈 昱（特级教师） 王甘雨

【教学困惑】为什么余数是20？

小学数学有一个学习内容是被除数和除数末尾都有0 的除法的简便算法。其算法依据是商不变规律，学习难点是理解并掌握确定余数的方法，如900÷40，余数为什么是20 而不是2？有不少数学教师在确定余数时自己都有疑惑，笔者常在各种教研群里见到此类问题的热烈讨论；即便教师知道确定余数的方法与原理，在课堂上也难以让学生理解而真正学懂。

对于这个问题，某配套《教师教学用书》给出如下教学建议：组织学生讨论，使之认识到被除数和除数的末尾同时去掉一个“0”后，算式表示90 个十除以4个十，算出的余数表示还剩2 个十，所以余数是20。但是，在实际课堂上，这样的算理学生不容易明白，反而会陷入误区：余数2 既然表示2 个十，那商22 也应该是22 个十，因为它们在百位和十位上……

面对如此教学窘境，我们该如何应对？只靠上面的机械说理远不能为学生解惑，要解决这个问题，还得回归被除数和除数末尾都有0 的除法的简便算法的数学本质，辅以具体实例。课堂上笔者试着运用“商不变规律”有效化解难题，还意外激发出学生对这一简便算法的“情境版演绎”。

【教学突破】基于商不变规律

课堂上学生提出“余数是20，商是220”后，笔者灵机一动立即想到要拿起“商不变规律”这个武器，于是有了如下教学：

师：大家看这个简便算法，商是220 吗？

生1：商是220 就不对了，我验算过了。

生2：可是那个2 明明在十位上啊！

师：我们进行这样的简便算法，依据是什么？

生：商不变规律！被除数和除数同时除以10，商不变。

师：是呀！商-不-变呀！

生3：根据商不变规律，这里的商应该还是22 才对（注：聚焦简便算法前，学生自主计算环节，有出现直接算900 除以40 商22 余20）。

师：与刚才的笔算相比，简便算法的竖式什么变了，什么没有变？

生4：在简便算法的竖式里，被除数和除数都缩小了10 倍，商没有变。（注：“缩小10 倍”是习惯说法，就是“缩小到原数的”，下同）

生2：我明白了！简便算法就是一种神奇的算法，在这里，被除数和除数缩小了10 倍，余数也跟着缩小了10 倍，但是商却保持不变。

师：说得真好！这种算法之所以神奇，是因为它用到了一个重要的规律，那就是？

生：商不变规律！

师：那现在你会将横式写完整吗？动笔写一写。

生5：我写好了，我想提醒大家注意，横式上的商和竖式的一样，横式上的余数跟竖式的不一样，得添个0。

生6：我有个更好的想法！这个竖式就相当于一个神奇的“缩小空间”！

师：“缩小空间”？听起来就很神奇！你可以解释一下吗？

生6：你们看，这个竖式就是一个“缩小空间”，要进入这个空间，什么都必须缩小10 倍，像被除数、除数和余数都缩小了10 倍；但商除外，因为商有“尚方宝剑”，这个尚方宝剑就是商不变规律。

生7：好想法！我有补充，我们填写横式或者写答语时，就好比跳出了“缩小空间”，这时候那些数字就会恢复“真身”，余数就要还原成缩小前的20，商一直不变。

师：你们的发言太精彩了，多么神奇的“缩小空间”啊！从大家的表情看，我知道你们都深深懂得了其中的道理。我还有另一个版本的解释：被除数和除数的末尾同时去掉一个“0”后，算式表示90 个十除以4个十，算出的余数表示还剩2 个十，所以余数是20。至于商为什么还是22，在学习商不变规律时大家应该就已经明白，900 里最多有22 个40，90（个十）里最多有22 个4（个十）。

以上教学之所以能突破学生的认知难点，为广大学生普遍接受，主要是因为回归了问题的数学本质，紧扣商不变规律来引导学生理解。一方面运用商不变规律化解了被除数和除数末尾都有0 的除法的简便算法的算理困惑，另一方面也深化了对商不变规律的理解。教学围绕学生的理解分不同层次推进：学生自由理解——引用商不变规律理解——学生创造性理解——算理性理解，如此这般，由里及外扫除学生的理解障碍，真正做到为理解和掌握而教，数学学习也得以真实地发生。

【应用掌握】充分理解和说明算理

为了加深学生理解，笔者设计了一份课后的“画计算”作业：画出400÷70 的简便算法，将每一步的算理表达清楚。学生的表现可圈可点，充分体现了他们对这一学习难点的深刻领会（如图1～4）。

图1

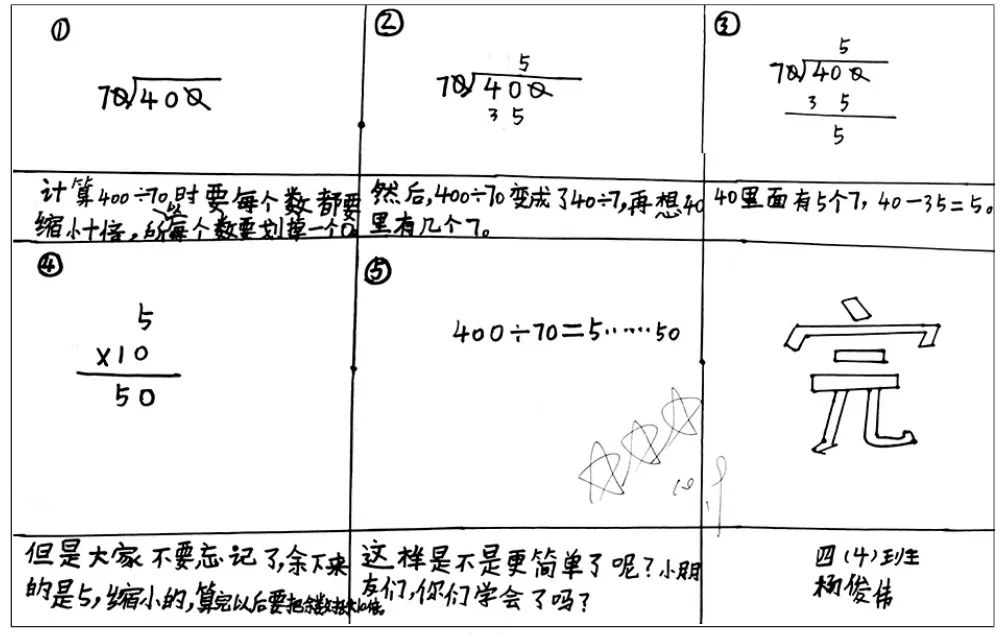
图2

图3

图4

学生对这一内容有了较为深入的认识，当他们在单元测试中遇到相关问题时表现出了非常难得的应用所学知识解决问题的能力。如图5 所示，这是一道除法算式题，题目要求“用你喜欢的方法计算”，大部分学生像图中左边那样用竖式计算，得到“商26 余12”；少数学生像图中右边那样利用除法的性质简算，得到“商26 余4”“商26 余2”“商26 余6”几种结果。于是问题来了：算法不同，这些算法都是有根有据的，商也都一样，为什么余数不一样呢？问题出在哪儿？

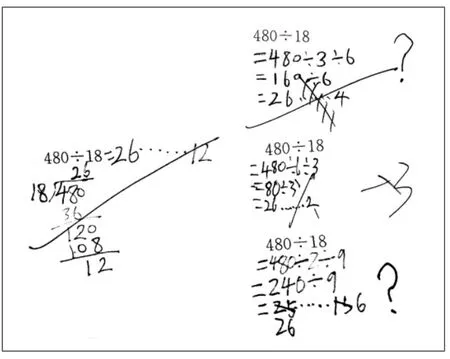
图5

经过独立思考，学生有了自己的想法。生1 最先陈述观点，还画出了自己的思考（如图6），她经过“试验”和比较，认为“一定是余数搞的鬼”，并发现有余数的除法算式不可以利用除法的性质简算。

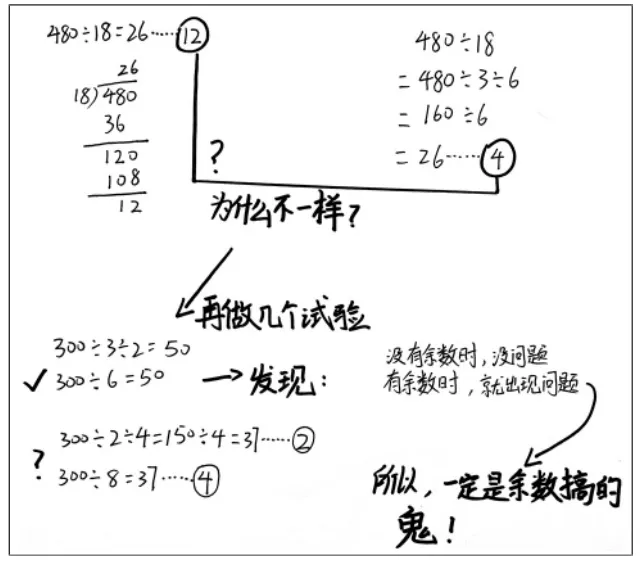
图6

生2 也有类似的想法（如图7）：480÷18=26……12 是对的，因为在有余数的除法算式中，除数越大余数就越大（除数越小余数也越小），而简便算法（指利用除法的性质）把除数变小了，余数也就变小了，所以简便算法只可以算没有余数的除法。

图7

此时，笔者追问：商26 余12 是谁的计算结果？商26 余4 呢？在简算的过程中发生了什么改变？原来的余数12 是怎样变成4、2、6 的？请大家想一想，小组内议一议。

全班交流环节，大家得出一致的看法：商26 余12 是480÷18 的结果；商26 余4 是160÷6 的结果，相当于进入缩小空间，把被除数、除数同时缩小3 倍，根据商不变规律，商不变，但余数也缩小了3 倍变成了4，要想写出480÷18 的结果，需要将余数4 扩大3 倍还原成12 才行；商26 余2 是80÷3 的结果，被除数、除数、余数同时缩小了6 倍；商26 余6 是240÷9 的结果，被除数、除数、余数同时缩小了2 倍……

至此，学生对商不变规律、除法的性质、有余数的除法等知识有了较为深刻且本质的认知，从而体味出数学本身的无穷魅力。

【研究聚焦】“代言画”的产生背景与教学价值

上例中“画出400÷70 的简便算法”其实是“画计算”中的一种形式，这种形式也叫为竖式代言的“代言画”。“代言画”一般基于算式，用精炼的文字辅以箭头等符号说明计算的算法与算理。除了“代言画”，“画计算”的形式主要还有实物画、几何图形画、点阵画、模型画、数式画等（见表1）。

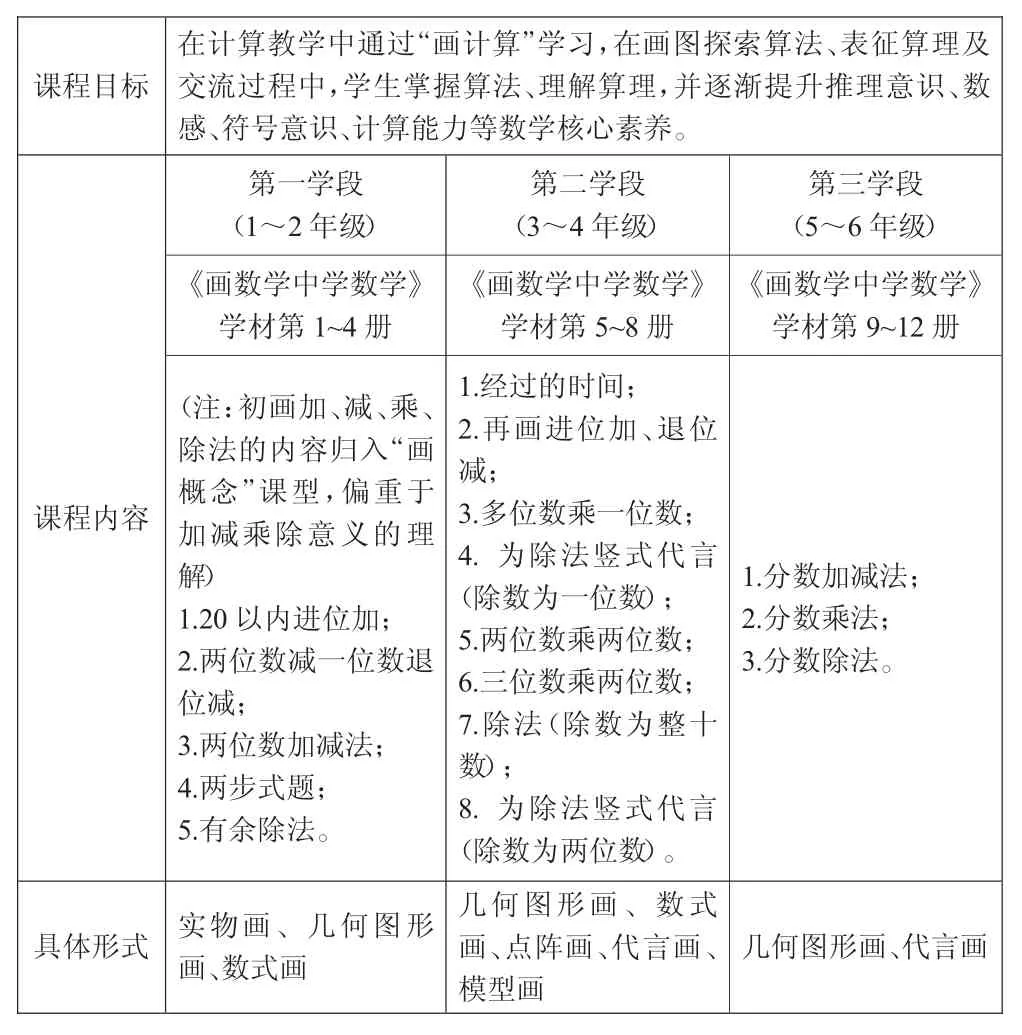
表1 “画计算”课程简表

“画计算”诸多形式的产生主要基于学生的认知心理特征和具体计算的表征需要。一年级学生偏向于实物画，并且很快就自发对所画实物加以简化和符号化处理，如表2 中实物画实例就是简化后的小棒图，所以只需稍加引导，学生就能掌握最常见、最重要的形式——几何图形画。随着学生年龄和计算数据的增大，一方面，学生觉得没有必要继续画实物或图形，于是就产生了直接在算式上画计算思考过程的数式画；另一方面，一些较复杂计算如果再用几何图形画就显得非常繁复（如图8），由此点阵画、模型画、代言画应运而生。点阵画、面积模型画、点线模型画还带有较强的“以形助数”“以形象表征抽象”的属性，其中点线模型画结构特别精妙，不仅含有点阵画的意思，而且蕴含着类似于“位值”的“线值”意义；而地锦模型画、数式画、代言画基本已经不具备这种属性了，其中地锦模型画像竖式一样，更多只是计算过程的一种记录。尽管在以形助数程度方面有差异，但是所有的“画计算”形式都能够较清楚地表征和解释计算思维。

表2 “画计算”主要形式举例

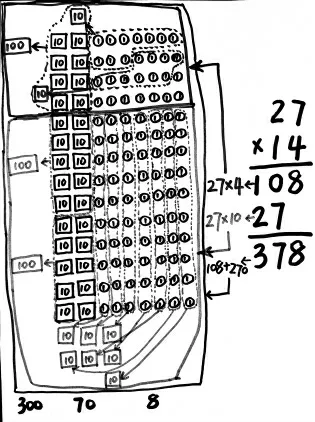
图8

这样一梳理，不难看出“代言画”对计算的表征不再依赖直观图形，而是付诸圈画与文字符号，同数式画一样是一种“符号画”。它可以基于算式本身加以说明，具有很强的灵活性和适应性，可以避免像其他主要利用直观图形的形式那样出现繁复、难以表征等现象，且保留了“数学画”的作品属性和理解功能，同样能够激发学生的创作欲望和学习兴趣，亦能够促进学生的数学理解，从而可以在更大范围上加以教学应用。

“代言画”的产生及广泛的教学应用也凸显了“数学画”教学提倡多元表征、不惟画图、兼容并包的教学理念与价值追求。“代言人”的角色带入与学习主人意识给予学生的不仅仅是教学手段与技术层面的革新，也不仅仅是数学学科素养的增进，更涉及对“人”的尊重、对“全人”的培育。