基于海洋捕食者算法的移动机器人路径规划

董志民，乔 栋，朱守健，赵政宏

（1 山西大同大学煤炭工程学院 山西 大同 037009）

（2 山西大同大学建筑与测绘工程学院 山西 大同 037003）

0 引言

自20 世纪90 年代以来，我们的国家一直致力于探索和推广移动机器人的应用和研究，许多科学院校和企业也积极投入到这项技术的研发中，他们不仅解决了定位、导航、硬件结构的技术挑战，而且还为这一领域的进步提供了有力的支持。 随着机器人领域的发展，路径规划已经成为移动机器人的关键部分［1］，它不仅仅涉及数学上的优化，而且还涉及实际应用，其复杂的结构、严格的限制条件以及对环境的影响，使得它成为当今科学家们关注的焦点。

传统的搜索算法如D*算法［2］、A*算法［3］和Dijkstra算法［4］通过栅格网络地图可以搜索出一条最优路径，但是算法本身具有效率低、速度慢等特点，随着问题规模的扩大，所花费的时间和消耗的内存也会成比例增加。 为了解决这一问题，学者们结合已有的方法和各种策略来解决路径规划问题，其中智能优化算法在机器人路径规划中应用越来越广泛。

近些年来，随着人工智能技术的提高，智能优化算法已成为解决路径规划的主要方法，例如蚁群算法、粒子群优化算法、遗传算法，因为该类算法在复杂情况下所消耗的计算代价和时间等都优于传统的路径规划方法［5-6］。

1 移动机器人路径规划

路径规划是移动机器人研究的重要领域，对机器人的日常工作和运动起着不可或缺的作用。 机器人的路径规划就是将各个传感器的信息结合然后根据一定的约束条件情况下，从起点到终点规划出一条适合机器人运动的路径［7-8］。 例如不能碰撞到障碍物的硬性约束、要求能耗最低、耗时最短等，进而达到一条最优的适合机器人运动的轨迹。 为了达到这一目的，机器人的路径规划任务一般分为以下3 个步骤：①环境仿真；②通过算法可以构建一条有效的路径；③通过路径平滑技术来提升机器人实际运动中的性能。

2 海洋捕食者算法

海洋捕食者算法由Afshin Faramarzi 等在2020 年提出，它基于元启发式优化算法。 海洋捕食者可以利用Lévy和布朗策略来规划行进步长找到最合适的觅食方式，而这种新的捕食策略在寻优能力上有更高的优势，一个顶级捕食者就是一个问题的解，而这些顶级捕食者们可以构成一个精英矩阵，通过算法的一系列优化操作，最后计算该矩阵中适应度值最小的一组即为最优解［9-11］。

2.1 构建精英矩阵（Elite）和猎物矩阵（Prey）

猎物矩阵（Prey）每一个元素Xi，j的初始化方法如式（1）所示：

式（1）中，Xmin和Xmax分别表示种群变量的上下限，rand ∈（1，0） 为服从均匀分布的随机向量。

精英捕食者矩阵Elite和猎物矩阵Prey分别如式（2）和式（3）所示：

式（2）、式（3）中，N 是种群的规模，D 是每个维度的位置（问题的解的维度）。

2.1 海洋捕食者算法优化阶段

2.1.1 迭代初期

在迭代初期，猎物的速度明显高于捕食者，它们遵循布朗运动，捕食者则主要进行探索活动。 此时迭代次数为总迭代次数的前三分之一，基于海洋捕食者算法优化的勘探策略，可以通过数学公式描述来实现捕食者的优化策略，如式（4）、式（5）所示：

式（4）、式（5）中，stepsizei为移动步长；RB为呈正态分布的布朗游走随机变量；Elitei为由顶级捕食者构造的精英矩阵；Preyi为与精英矩阵具有相同维数的猎物矩阵；⊗为逐项乘法运算符；P为0.5；R 为［0，1］内均匀分布的随机变量；n为种群规模；Iter和Max_Iter分别为当前迭代次数和最大迭代次数。

2.1.2 迭代中期

在迭代的中期，迭代次数占总迭代次数的三分之一到三分之二之间。 算法从原本的勘探策略开始向更加灵活的开发策略转变。 此时捕食者与猎物速度相同，一半种群基于Lévy游走策略负责开发，另一半基于布朗游走策略负责勘探，数学描述如式（6）～（10）所示：

其中，RL为呈Lévy 分布的随机变量；CF 为控制捕食者步长的自适应时变参数。

2.1.3 迭代终期

在迭代终期又为开发阶段，此时为总迭代次数的后三分之一，猎物的行进速度低于捕食者的行进速度，它们会根据Lévy 策略来调整自身的行进步长。 其数学描述为式（11）、式（12）：

2.1.4 FADs 效应或涡流

人工集鱼装置（fish aggregation devices，FADs）或涡流效应为外部的环境干扰，通常可以改变海洋捕食者觅食行为，使用这一策略能使海洋捕食者算法在寻优过程中解决收敛过早和陷入局部最优等问题。 如式（13）所示：

式（13）中FADs 为解决过早收敛和陷入局部最优的影响因子，取值为0.2。Preyr1和Preyr2分别猎物矩阵的随机值，即选取随机两个猎物；U 为二进制向量；r 为［0，1］内的随机数。

2.2 算法流程

算法的实施过程包括5 个关键步骤。

步骤1：初始化算法参数，初始化种群。

步骤2：计算适应度值，记录最优位置。

步骤3：在迭代过程中，捕食者可以通过式（4）到式（13）来调整自身的位置，以达到最佳的捕食效果。

步骤4：计算适应度值，更新最优位置。

步骤5：判断是否满足停止条件，如果不满足则重复步骤3～5，否则输出算法最优结果。

依据海洋捕食者算法的基本思想，其流程可以按照图1 的描述。

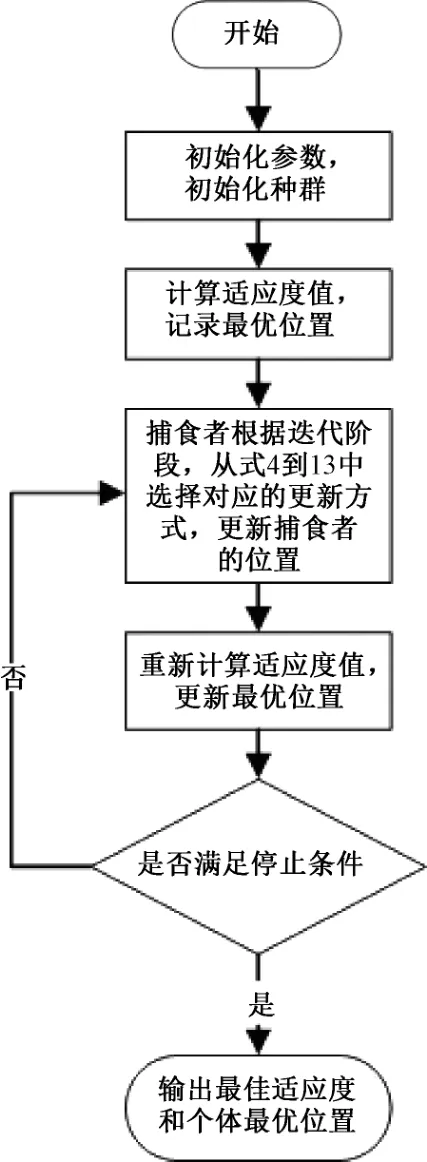
图1 海洋捕食者算法流程示意图

3 仿真实验

为模拟移动机器人的工作环境，本文使用栅格法描述工作环境信息，其目标函数可表示为式（14）：

式（14）中，L表示适应度值（路径的长度），n 表示路径上的每一个点的坐标。

使用MATLAB R2022a 仿真软件进行仿真。 两种算法的初始种群数量都是30，它们的最高迭代次数被限定在500。 地图中的起始点和终点分别位于（1，1）和（r，c）。 地图中黑色的格子代表不可通行区域，白色格子代表可通行区域。 选用三种地图测试该算法的性能。 为了验证算法结果不具有偶然性，每个算法在固定参数后都会运行30次取平均值。 两种算法在三种地图的路径规划规划结果及收敛如图2 所示。

图2 在3 种地图上的仿真实验

在经过30 次的仿真实验后，两种算法在30×30 的栅格地图下平均最短路径，平均迭代次数如表1～3 所示。

表1 粒子群优化算法和海洋捕食者算法在地图1 中的性能比较

表2 粒子群优化算法和海洋捕食者算法在地图2 中的性能比较

表3 粒子群优化算法和海洋捕食者算法在地图3 中的性能比较

根据以上图表和仿真信息可以得出，海洋捕食者算法的路径规划结果明显优于粒子群优化算法。 不仅所得到的路径长度比较PSO 算法要短，迭代次数也大幅度下降。地图1 中平均适应度下降3.5%，平均迭代次数下降32.8%；地图2 中平均适应度下降3.7%，平均迭代次数下降33.7%；地图3 中平均适应度下降2.2%，平均迭代次数下降46.4%。 由以上可得，海洋捕食者算法在最短路径和迭代次数上明显优于粒子群优化算法。

4 结语

本文首先分析了海洋捕食者的算法原理和流程，利用MATLAB R2022a 仿真软件进行仿真，将海洋捕食者算法和粒子群优化算法在3 种地图上做仿真实验，在障碍物部分不同的情况下发现海洋捕食者算法在迭代次数和适应度上都明显优于粒子群优化算法。 适应度平均下降3.06%，迭代次数平均下降了37.6%。 经过实验证明，采用海洋捕食者算法得出的路径精度极高，而且行进速度极快，完全能够满足移动机器人的路径规划需求。