一种新型六自由度并联机器人设计

陈飞，陈机林，候远龙

(南京理工大学机械工程学院，江苏南京 210094)

0 前言

随着并联机构的诞生，各种适应不同应用场合的并联机构层出不穷，但由于并联机构的某些特性，如工作空间和运动速度限制了其应用范围[1]。且常见并联机器人结构所用传动机构难以小型化，造成了并联机器人结构较大，空间利用率不足。本文作者设计了一种Z轴旋转运动不受限制的六自由度并联机器人。相对于常见的并联机器人，此并联机器人不需要齿轮传动，结构相对小巧，空间利用率较高。

文中除了介绍了这种并联机器人的结构以及运动原理，还对此并联机器人姿态位置的反解、受力情况以及运动所需的力矩和功率做了研究，为实际设计提供了理论依据。

1 并联机器人结构以及运动原理

1.1 Stewart并联机器人

1965年，英国人STEWART第一次提出六自由度的并联机构[2]，为了达到飞行员训练的目的，将其用作飞行模拟器。图1所示为一个经典的六自由度Stewart机械平台，它由6根独立伸缩的连杆将静平台和动平台连接，通过每个连杆不同的伸缩量使得动平台可以完成6个自由度的位置和姿态变化[3]，即在空间内可作任意方向平移以及绕任意方向的转动。

图1 并联机器人模型Fig.1 Parallel robot model

但这种并联机构结构相对复杂、整体尺寸较大，工作空间一般较小。

1.2 基于轴向电机的多转子六自由度并联机器人

为了扩大并联机器人的工作空间，减少整体尺寸，本文作者设计了一种新型并联机器人，如图2所示。此并联机器人由静平台、动平台、6个连杆、6个滑块以及12个球铰组成。其中静平台旋转布置多个线圈，滑块上贴有钕铁硼磁铁，通过不同线圈的通断控制滑块移动，可以将静平台视为定子，每个滑块视为转子共同组成其驱动部分。

图2 并联机器人模型Fig.2 Parallel robot model

此并联机器人的动平台位姿由6个滑台的旋转位置所决定，并且当滑台之间相对位置不变时同时增加驱动扭矩可以控制此六轴机器人绕静平台旋转。

2 机器人位姿反解

2.1 六自由度平台结构参数与坐标系建立

并联机器人模型如图2所示，该模型动平面由6个连杆与滑台连接。为了描述平台的运动，将该并联机器人抽象为一个空间几何模型，如图3所示。其中点1-6和7-12分别为静平台与动平台球铰的中心。

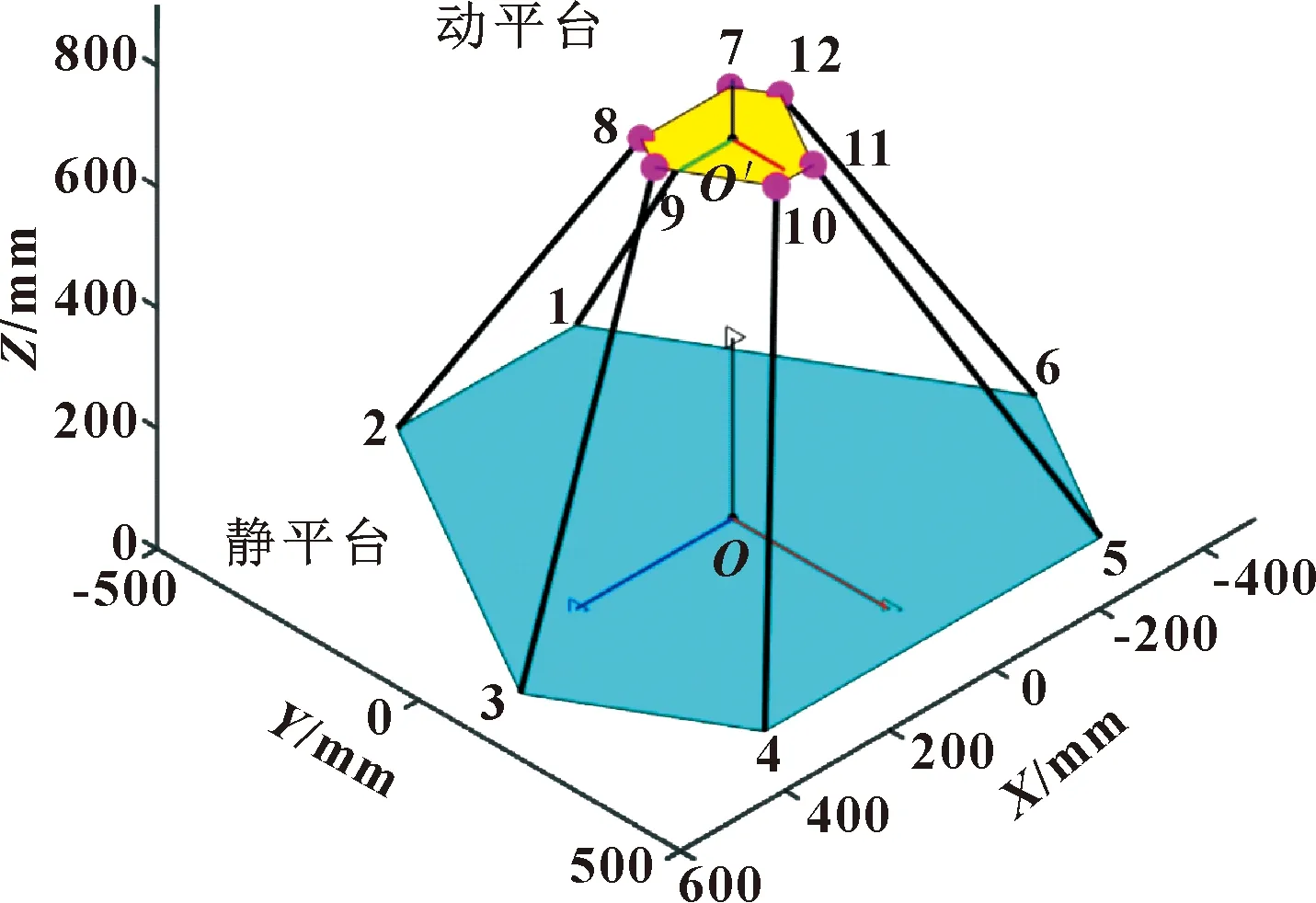
图3 空间几何模型Fig.3 Spatial geometry model

在平台中心构建两个坐标系，静坐标系OXYZ和动坐标系O′X′Y′Z′，如图3所示。其中动坐标系与动平台固联，其坐标原点位于动平台中心，X′Y′平面与动平台重合；静坐标系固定在大地上，坐标原点在静平台中心。在平台处于中位时，静坐标系与动坐标系平行，当动平台运动时，动坐标系随平台一起运动，而静坐标系始终静止不动。

定义并联机器人结构参数如表1所示。

表1 并联机器人尺寸参数Tab.1 Dimension parameters of parallel robot

2.2 运动学反解

运动学反解是在已知末端执行器的位置和姿态的情况下求解驱动器的运动量[4]。文中末端执行器为动平台，驱动器是6个滑台，可通过动平台位姿信息求解各滑台与X轴的夹角θ。

当动平台具有位姿Q=(αβγXYZ)时可以得到动平台绕动坐标系的旋转变换矩阵如下：

(1)

(2)

(3)

(4)

(5)

式中：RX(α)、RY(β)、RZ(γ)分别表示动平台绕静平台X、Y、Z轴旋转的旋转矩阵，以顺时针为正；P0为动平台相对静平台的位移；T为动坐标系到静坐标系的坐标变换矩阵。

对任意某支链分析，定义其连接动平台的球铰中心为点A，连接滑块球铰中心为点B，如图4所示。

可得OA=TO′A+P0

(6)

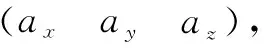
(7)

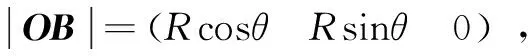
cosφ=ax·Rcosθ+ay·Rsinθ=

(8)

定义：

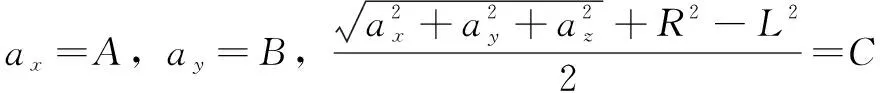
(9)

可知滑块i与X轴夹角θi，实际解算后θi有两解，即表示对于动平台的某一固定位姿Q，每个滑块有两个位置可以满足运动需求，实际运动中将造成滑块位置冲突，如图5所示。

图5 滑块位置冲突Fig.5 Slider position conflict

位置冲突会导致滑块相撞，可通过滑块之间相对位置避免。具体步骤为：由滑块大小可得两滑块互补相撞的最小夹角θmin，计算相邻两滑块之间角度差使其大于最小夹角θmin。滑块夹角示意如图6所示。

图6 滑块夹角示意Fig.6 The angle between the sliders

3 并联机器人应力分析

并联机器人的动力学研究方法有：牛顿-欧拉(Newton-Euler)方程、达朗伯原理-虚位移原理、拉格朗日(Lagrange)方程、高斯(Gauss)方法、凯恩(Kane)方法、螺旋理论等[5]。文中采用牛顿-欧拉方程求解，分析此并联机器人位姿Q的应力。

当动平台具有位姿Q=(αβγXYZ)时，由于此并联机器人的连杆为轻量化铝合金，为简化计算可将忽略其重力参数，视为二力杆。则定义以下参数便于计算，见表2。

表2 并联机器人运动参数Tab.2 Kinematic parameters of parallel robot

3.1 支链受力分析

3.2 滑块力分析

滑块视为一个刚体，其受支链的反作用力、底座向上的支持力和指向坐标原点的法向力、线圈绕组对滑块的拖拽力。其中滑块切向力仅只有线圈绕组切向的拖拽力、惯性力的切向分量与支链反作用力的切向分量。则有：

(10)

其中：Ti为线圈绕组的拖拽力切向分力。

3.3 动平台受力分析

动平台受6个支链的反作用力与动平台自身重力G，在动平台运动时还有惯性力与惯性力矩，其合力与合力矩为0。

在静坐标系下，动平台重力G、惯性力与6个支链的反作用力合力为0：

(11)

在动平台质心处，支链的反作用力矩、重力力矩以及惯性力矩满足

(12)

公式(11)(12)在静坐标系下可以分为X、Y、Z三轴的分量解算，得到一个6个未知数的方程组。

4 多转子结构

此并联机器人的驱动部分可以使用齿轮组合的方式通过固定在滑台的电机驱动小齿轮转动移动滑块，但齿轮组合的方式需要在滑台固定电机，增加了并联机器人的尺寸大小，且动平台绕Z轴旋转圈数增加时电机的电缆线会互相缠绕。为避免这种情况，本文作者设计了一种轴向电机的多转子驱动结构。

4.1 多转子结构

此并联机器人的底座与滑台结构，由类似轴向电机的方式组成[6-7]，如图7、8所示。

其底座含有多个线圈绕组，每个线圈绕组可单独通断。滑台含多个钕铁硼磁铁结构，在相近绕组接通后给予其动力，使得滑台在底座转动。通过控制相邻线圈绕组通过的电压大小可以使水平方向的拖拽力与滑台运动轨迹相切，其控制方式类似无刷电机FOC(Field-Oriented Control)控制[8]。此驱动方式的并联机器人活动结构无电线连接，避免了运动过程中电缆的限制，同时其线圈绕组内置在底座上，滑台上仅需贴上钕铁硼磁铁即可，大大减小其结构尺寸。

4.2 驱动扭矩与功率分析

滑台受力分为3个部分：支持力、轴向拉力以及切向力。其中切向力由线圈绕组提供。其驱动扭矩最大值由切向力决定，功率由滑块运动速度与切向力共同决定。

4.3 转子转矩加强方法

转子可提供的转矩决定了此并联机器人运动的快慢，要加强转子力矩除了增加线圈绕组通过的电流还可以通过如下两种方法：(1)增加滑台尺寸，增加其钕铁硼磁铁的对数。(2)改变钕铁硼磁铁的排列结构，将单个钕铁硼磁铁变为多个小的钕铁硼磁铁组成的强磁阵列[9]的结构，如图9所示。

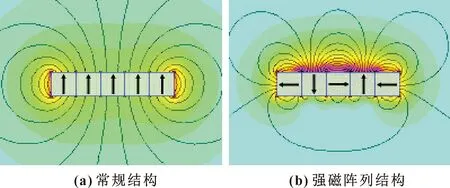
图9 钕铁硼磁铁的排列结构Fig.9 The arrangement structure of NdFeB magnet：(a) conventional structure；(b)strong magnetic array structure

5 结论

常规的六自由度并联机器人空间运动范围有限，本文作者提出一种新型并联机器人，具有Z轴转动不受限制的特点，极大地扩展了其运动范围；且此并联机器人驱动部分仅有线圈和钕铁硼磁铁组合，可以视为一个拆解的轴向电机，避免了齿轮传动结构，还具有轴向电机结构尺寸小、动力大等优点；相对常规并联机器人结构尺寸极大减少，对并联机器人的设计有一定的启发作用。本文作者还提供了此并联机器人运动姿态反解、运动受力分析，以及驱动器设计所需的几个重要参数来源，便于实际设计。