机器人曲面抛光末端VCM力迭代学习控制研究

黄海滨，傅亭硕，王同特，程华康，邹朝圣

(1.厦门理工学院机械与汽车工程学院，福建厦门 361024；2.厦门万久科技股份有限公司，福建厦门 361025)

0 前言

曲面元件表面由一系列相互之间没有几何约束的离散点构成，因其具备特殊力学特性和功能[1]，应用领域愈发广泛与重要。采用机器人串联执行器、执行器主动输出抛光力的加工方式，控制机器人运动姿态顺应元件表面低频特征——轮廓与曲率变化，控制执行器输出恒定抛光力保证材料去除量一致，减小元件表面中频误差——波纹度和高频误差——表面粗糙度，融合了机器人柔性好、工作空间大、执行器力控精度高、响应速度快的特点，可有效提高加工效率，改善加工质量，适用更精密的加工要求。

由于机器人抛光系统非线性强耦合的特点，加工过程中精确控制运动位置和抛光力难度较大。力/位混合控制策略引入选择矩阵将工件表面进行切向和法向划分，直接对二者进行控制。文献[2]提出一种基于内关节转矩的力/位混合控制方法，利用内置传感器对抛光力进行反馈和控制，但是诸多工业机器人底层转矩控制不开放，力/位混合控制在硬件条件上有一定的局限性。阻抗控制策略通过力与位置的动态关系间接实现柔顺控制。文献[3]在阻抗模型的基础上设计一个自适应抗饱和积分模糊PI控制器，有效防止了不良震动和机械碰撞。由于阻抗控制的本质是通过调整机器人位置和运动速度间接实现力控制，加之作业环境的非线性扰动、六轴之间的串联关系，以及力传感器与机器人来自不同品牌、底层算法不兼容带来的通信迟滞问题，使得机器人阻抗控制在实际抛光中常会存在几百毫秒级的延迟现象，带来了过抛的问题，延迟过大甚至导致系统失稳，无法满足高精密加工要求。因此末端执行器在旋转抛光的基础上加入主动力控功能，使整体抛光系统性能有进一步提升[4]。文献[5]研究一种气电混合式末端执行器，用于表面变化平缓型工件自动化抛光打磨作业。文献[6]设计一种电驱动直线末端执行器，建立了机器人-执行器宏微控制模型，提出基于自适应阻抗控制的研磨策略完成了磨抛加工。

由以上分析可知柔顺抛光系统要满足高精密加工要求并具备普适性还具有一定难度。本文作者设计一种力主动输出式执行器，采用切片算法计算抛光轨迹实时控制机器人运动位置，以力控电机的输出电流为控制目标，提出基于迭代学习控制的力控策略实时迭代优化输出电流以稳定抛光力，设计一套融合力控制和位置控制两独立系统的曲面元件柔顺抛光系统，使机器人与执行器在各自任务空间单独工作，避免力位耦合互相干扰。

1 柔顺抛光系统组成

1.1 系统介绍

柔顺抛光系统原理如图1所示，主要包括上位机、ABB IRB 4600工业机器人、机器人控制柜、控制卡以及末端执行器。系统整体工作示意如图2所示，工作原理如下：运动控制系统根据不同曲面轮廓特征提前更新轨迹程序以控制机器人运动，当执行器末端抛光盘接触到工件时，控制卡采集模块读取到六维力传感器的压力信号，力控系统根据实时力信息完成数据处理，发送控制信号给力控电机驱动器完成恒力控制。

图1 柔顺抛光系统原理Fig.1 Principle of the smooth polishing system

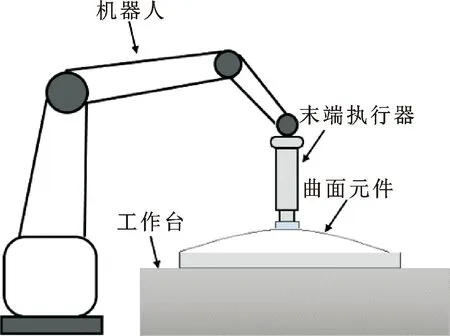
图2 工作示意Fig.2 Working schematic

1.2 执行器设计

执行器具体结构如图3所示。因为音圈电机具有快响应、高精密、结构简易的特点[7]，故用其作为执行器的力控电机。机构整体为对称结构，两侧各设计两组导轨滑块以保证运动精度。其中六维力传感器、力控电机和抛光电机是执行器的主要部件，此外还包括安装法兰、导轨、限位块、轴承安装座、抛光盘等。力传感器安装于直线电机动子下方，避免其运动导致力传感器负载部分重心变化而影响重力补偿的准确性。执行器有直线方向25 mm可自由伸缩空间，能够降低对曲面元件三维模型的精度要求，补偿一定的工件和工具坐标系误差以及机器人轨迹误差。

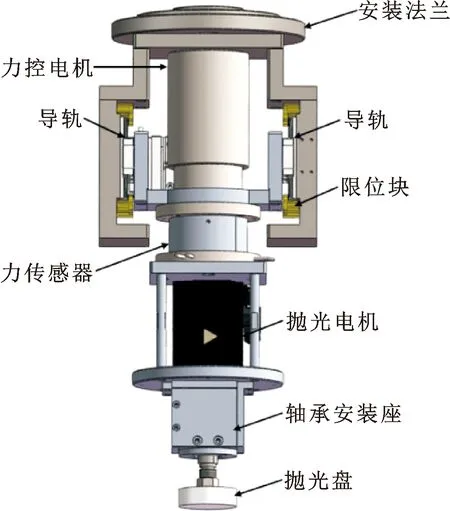
图3 执行器结构图设计Fig.3 Actuator structure design

执行器工作流程如下：工作开始时，设定音圈电机初始电流达到目标抛光力，同时启动旋转电机；当抛光盘接触到工件时，随着工件曲率的变化接触力出现波动，力传感器将压力信号反馈给控制卡，控制卡根据信号偏差调整电流大小发送到电机驱动器完成抛光力控制。音圈电机持续峰值推力271.1 N，持续推力115 N，力灵敏度为26.2 N/A。抛光加工为持续接触式作业方式，控制输出力在持续推力范围以内工作更为安全稳定，对应电流为-4.39～4.39 A。若以最大电流4.39 A持续推出，外加电机动子重力与负载45.6 N，可输出160.6 N最大推力，考虑机器人带动执行器运动导致姿态变化对动子负载产生的影响，可得执行器可控输出力范围为0～150 N，满足工业抛光力需要。

力控信号响应时间包含指令发送时间与执行器执行时间，在实际测试中还加上了数据回传的时间使得测试值稍有变大。随机取50次信号发送指令，响应曲线如图4所示，响应时间均值t=55.4 ms，达到了高响应要求。

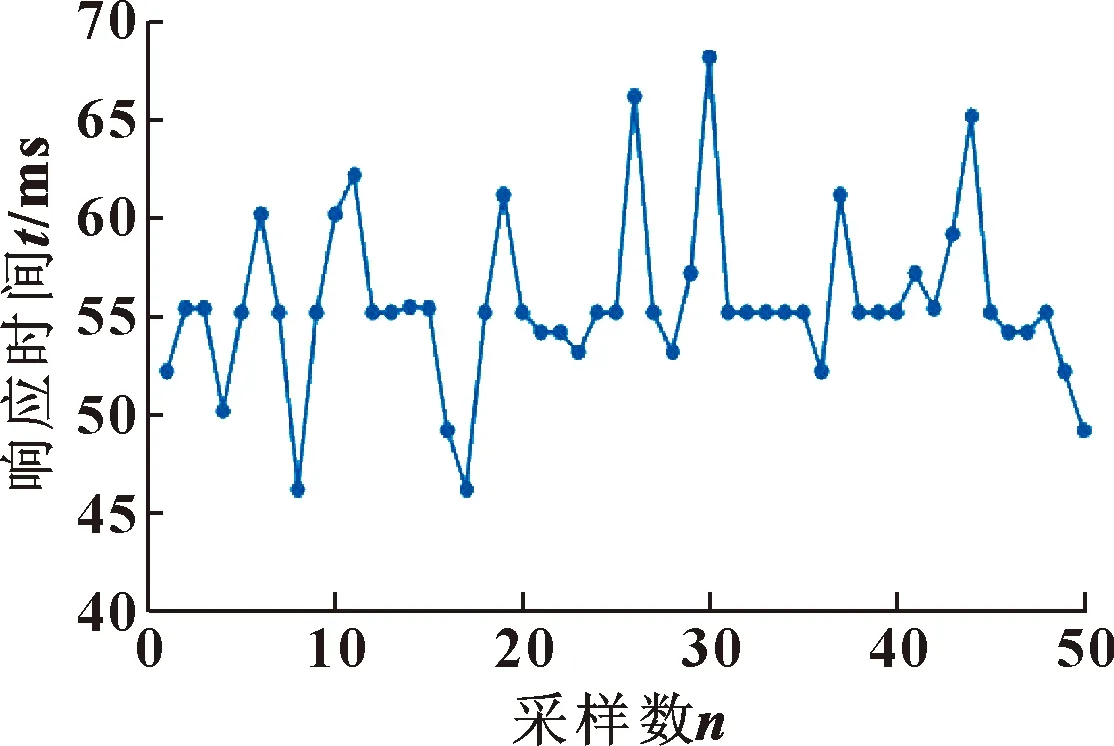
图4 执行器响应时间测试结果Fig.4 Actuator response time test result

2 柔顺控制方案

2.1 机器人运动控制

根据元件的三维模型获取其STL文件，提取文件数据并处理冗余数据，建立拓扑关系；采用切片算法获取抛光路径点坐标，根据工件实际尺寸、面型以及抛光盘大小，设置切片方向和间距大小；交点集通过排序法则处理以生成抛光轨迹线，计算路径点法失确保抛光工具始终沿着交点坐标法向方向，算出机器人末端抛光工具的旋转矩阵并转换成对应的四元数信息；最后按照ABB机器人能够运行的Rapid语言格式进行运行程序的编写，导入上位软件中并设定好机器人运动速度实现机器人运动控制。图5所示为规划路径示意，黄色线条为机器人运动方向，整体为光栅轨迹，绿色与红色线交点为所计算出的机器人运动目标点。

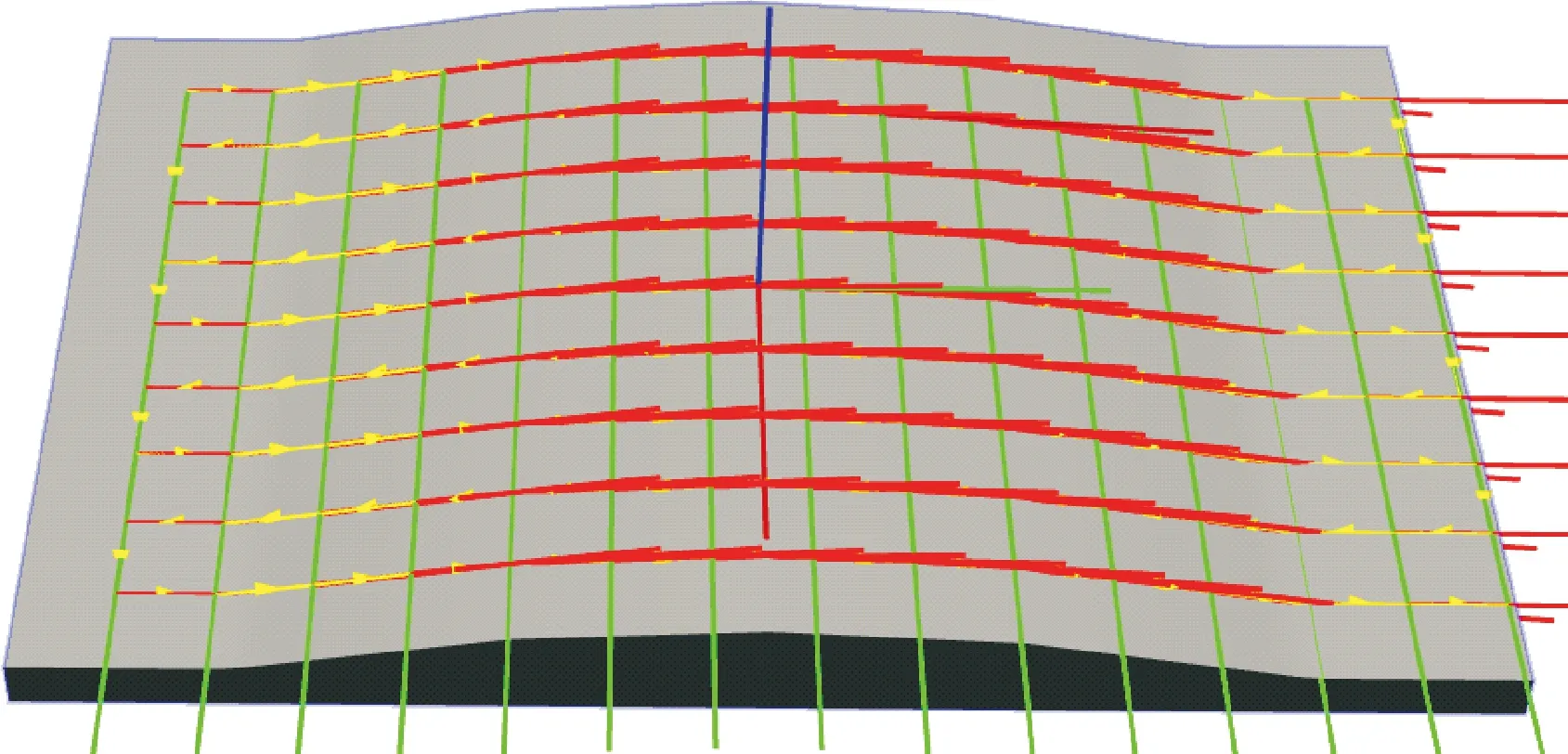
图5 抛光轨迹规划Fig.5 Polishing trajectory planning

2.2 执行器数学模型建立

根据执行器的结构可知，音圈电机为系统输出力元件，假设运动方向向下，对该装置进行受力分析，如图6所示。由牛顿第二定律可得系统的力学平衡方程如下：

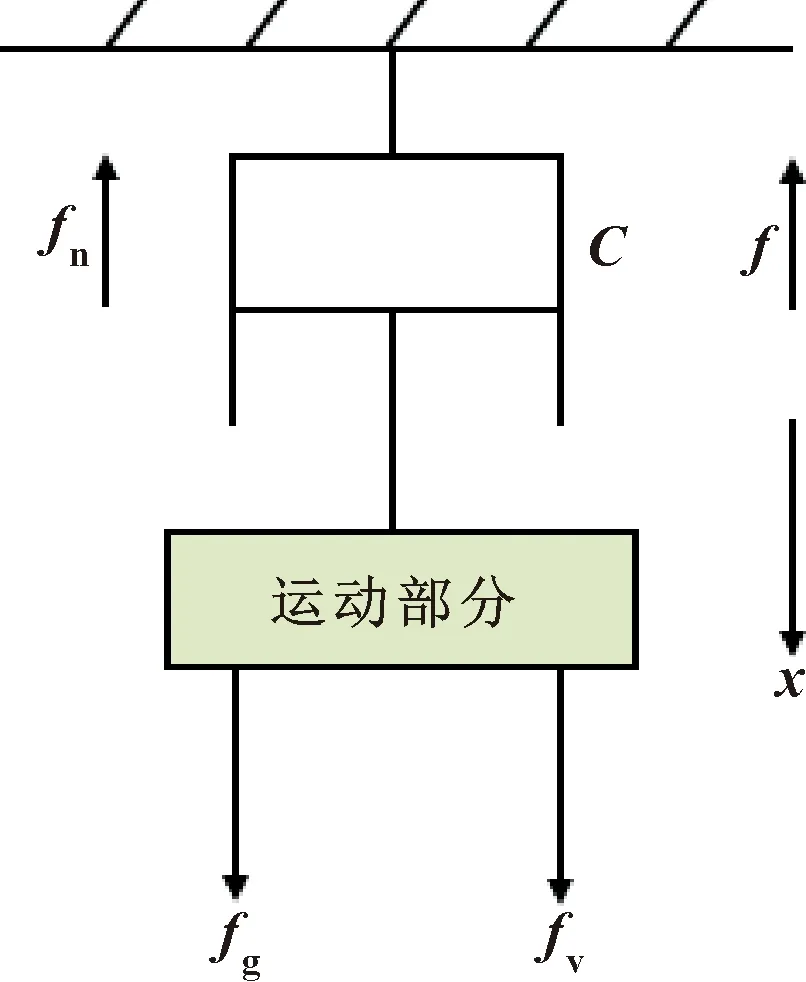
图6 执行器受力分析Fig.6 Actuator force analysis

fv+fg-fn-fc=ma

(1)

式中：fv为音圈电机输出力；fg为运动部分重力；fn和fc分别为系统所受支持力和阻尼力。

另外，音圈电机等效电路模型如图7所示。根据基尔霍夫电压定律可得系统电压平衡方程如下：

图7 执行器电路模型Fig.7 Actuator circuit model

(2)

式中：R为电阻；L为电感；B为磁感应强度；l为导线长度；v为运动速度；Blv为音圈电机反电动势。根据洛仑兹定律可知执行器输出力为

fv=Bil=kvi

(3)

式中：kv为电机推力系数；i为通过电机线圈电流。

实际抛光中工具与工件稳定接触，重力与支持力相互抵消，将式(1)—(3)进行拉普拉斯变化，得

于是执行器输出力传递函数为

(4)

2.3 迭代学习控制器设计

本文作者采用控制电机电流的方式调整抛光压力。电流的大小直接影响执行器输出力，且电流环独立控制内部系统，不会受到机械运动的影响[8]，是提高力控系统响应与精度的有效着力点。系统控制框图如图8所示：fe为期望力；fa为实际接触力；e0为力偏差；id为期望电流；i为实际输出电流；e1为电流偏差；kv为电机推力系数；fv为执行器输出力；fd为干扰力。

图8 系统控制框图Fig.8 System control block diagram

由图8可知，力环控制器仅需要完成期望电流的运算，因此使用传统的PID算法即可。电流环则需要高精度高响应跟踪目标电流以稳定执行器抛光力，迭代学习控制适用于重复控制场景，以先前经验和偏差修正当前控制量，能够满足良好的轨迹和目标值跟踪，本文作者采用的带遗忘因子的PD型闭环迭代学习控制器，结构如图9所示。

算法描述如下：

(5)

2.4 收敛性分析

由上述分析可将执行器描述成如下系统：

(6)

其中：xk(t)、uk(t)、yk(t)分别为系统状态变量、输入向量和输出向量；A、B、C为常系数矩阵；t为时间变量；k为迭代次数。

证明[9]：由式(5)可知第k+1次控制输入误差为

(7)

其中：

(8)

由式(6)解得xd(t)与xk+1(t)并代入式(8)中，得：

ek+1(t)=CeAt[xd(0)-xk+1(0)]+

结合初值条件可知：

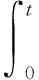
(9)

对式(9)两边做微分，有

(10)

将式(9)(10)代入式(7)中得

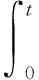
AΓ)eA(t-σ)ΔUk+1(σ)dσ

记E=1-h，F=C(Φ+AΓ)， 则

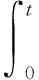
(11)

对式(11)两端取范数，得

将上式两侧同时乘以e-αt，t∈[0，T]，并利用不等式放缩将eA(t-σ)放缩，得

(12)

根据λ范数的定义，式(12)可化为

(13)

化简得：

(14)

则当λ取值足够大时，有

(15)

(16)

由式(9)知：

(17)

2.5 仿真分析

图10 仿真结果Fig.10 Simulation results

从仿真结果可以看出，常规PID控制器虽然可以使系统达到稳态，但是其存在明显的超调，且调节时间较长。根据迭代学习控制收敛性证明知当迭代次数k无限多时，系统会理想地跟踪目标值，但必然会影响实际加工的效率。仿真中通过1次、3次、5次和20次迭代，验证了算法稳定的跟踪性能，当迭代20次时，系统能快速跟踪目标值，满足实际加工中的效率要求。

3 曲面抛光实验与分析

为了验证上述所设计执行器的工作性能，与所提出控制方法在实际工作中的可行性，现搭建一套柔顺抛光系统，如图11所示。系统柔顺性主要通过实验过程中的恒力跟踪性能体现。

图11 机器人柔顺抛光系统Fig.11 Robotic smooth polishing system

实验中所抛光的曲面元件如图12所示，其材质为6061铝合金，尺寸为200 mm×300 mm，最大高度25 mm。为达到更好的抛光效果，先使用羊毛毡以30 N目标力进行初抛，再使用海绵以15 N目标力进行精抛。

实验中首先观察机器人实际运动中能否较好适应元件曲率变化，在元件曲率较大处末端抛光盘与元件表面接触情况如图13所示。可看出抛光系统对曲面曲率适应性良好，但是工作前的标定和坐标系建立过程带来的误差以及三维模型的偏差和机器人运动误差，导致仅基于轨迹规划的曲面抛光过程中压力波动明显。设置目标力30 N，实际加工中六维力传感器抛光压力信息如图14所示。

图14中无力控抛光力偏差绝对值为8 N。工程领域要求抛光力波动稳定在5 N以内[10]。加入力控模式以30 N压力初抛和15 N压力精抛，实际力信息曲线如图15—16所示。可得出在两种抛光压力参数下力偏差绝对值均能控制在3 N以内，可满足实际抛光要求。

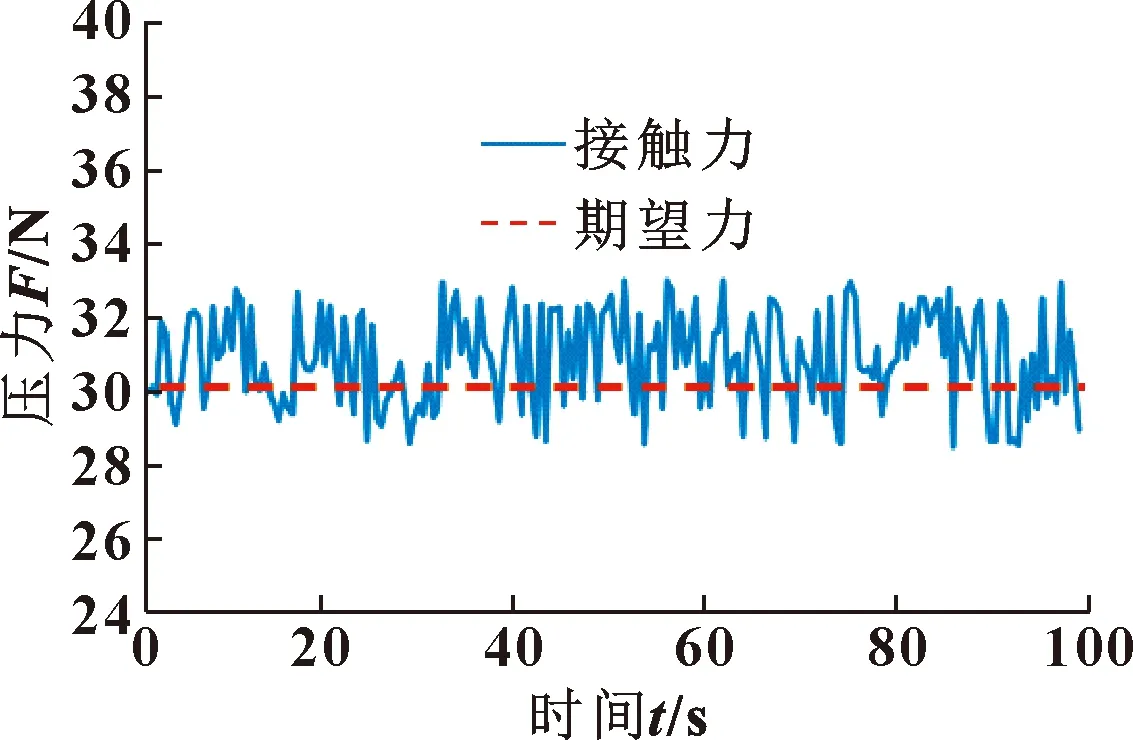
图15 目标力30 N控制效果Fig.15 Target force 30 N control effect

图16 目标力15 N控制效果Fig.16 Target force 15 N control effect

4 结论

针对曲面元件机器人抛光中抛光力稳定性以及机器人延迟问题，本文作者提出一种主动式力控末端执行器并进行轻量化设计，使其与机器人协同完成曲面力控抛光。在建立其机制模型基础上结合迭代学习控制理论，设计迭代学习控制器优化抛光力输出，并对控制器做了相应仿真分析。该方法以电机内环电流为目标直接控制抛光力，抗干扰能力强。最后通过实验验证了该柔顺系统适用于曲面元件抛光加工，能够以高精度、高响应跟踪目标力。