基于参数解耦陷波滤波器的工业机器人末端振动抑制

潘海鸿，丁可帅，吴锡鹏，陈琳，梁旭斌

(广西大学机械工程学院，广西南宁 530004)

0 前言

对于工业机器人而言，由于电机和与连杆之间传动装置并非都是刚性材质，使得机器人在响应起动或停止指令的过程中产生定位振动的现象，严重降低机器人运动时的精度，导致系统不稳定[1]。为解决工业机器人由于传动装置刚性不足所引发的定位振动问题，国内外学者已经在多个方面进行了研究，提出了诸多抑制方案，大致可分为3种方式：物理抑制方式、主动抑制方式和被动抑制方式[2-3]。

物理抑制方式是通过机械结构优化设计改变系统固有频率，增大阻尼比，或选择耗能和储能材料降低柔性变形，抑制振动[4]。主动抑制方式通常是根据电机编码器等外部传感器的反馈设计控制器，同时配合伺服参数自整定实现机器人末端振动抑制，改善整个系统的动态特性[5]，常见方法有：观测器法、力矩前馈控制和输入整形法等[6-11]。黄梁松等[7]通过扰动观测器的方法调节系统惯性比，将比值设置为适当的值，从而达到抑制扭振的效果。ZHANG 等[8]为实现工业机器人高精度控制，提出实时力矩前馈控制方法，实验结果表明：轨迹跟踪误差和抖动明显下降。ZHANG等[9]构造了一个简单的优化器选择和输入整形器的最优参数，与根据辨识模型确定的整形器参数相比，振动抑制效果更好。被动抑制方式主要是在不改变系统控制结构的基础上，通过使用补偿或校正方法对振动固有频率进行抑制[12]。常用的方法是处理位置指令输入信号，除去给定的位置指令中振动相关频率分量，从而达到抑制振动的目的[13]。张铁等人[14]通过力锤实验获取工业机器人的振动信息，设计陷波滤波器抑制振动，但实验方法复杂，实验成本高。

针对陷波滤波器在解决六自由度工业机器人伺服系统定位振动问题时所面临的滤波器参数存在耦合、不便于参数整定的缺点，提出一种参数解耦陷波滤波器，对传统陷波滤波器参数解耦，利用傅里叶变换和对数衰减法快速整定滤波器参数，最后通过实验验证该方法对抑制振动的有效性。

1 柔性关节模型与定位振动分析

1.1 柔性关节双惯量模型的建立

通常情况下将由伺服电机、传动装置和关节组成的伺服系统简化为一个柔性关节双惯量传动模型(图1)。其中，JM、JL分别为电机和负载的惯量；Ks为传动机构的刚度系数；N为减速器减速比；TM、TL和TW分别为电机输出转矩、负载转矩和转动轴扭转转矩；bM、bL和bs分别为电机、负载和传动机构的阻尼系数；θM、θL、ωM和ωL分别为电机和负载的角度和角速度。

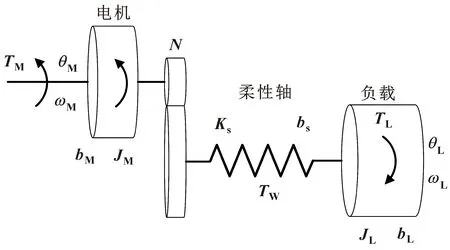
图1 柔性关节双惯量传动模型Fig.1 Flexible joint double inertia transmission model

根据关节双惯量模型，可以得到系统平衡方程：

(1)

由于系统中的阻尼系数很小，可将其忽略。然后对系统微分方程组进行拉普拉斯变换得：

(2)

由式(2)可得双惯量系统框图如图2所示。

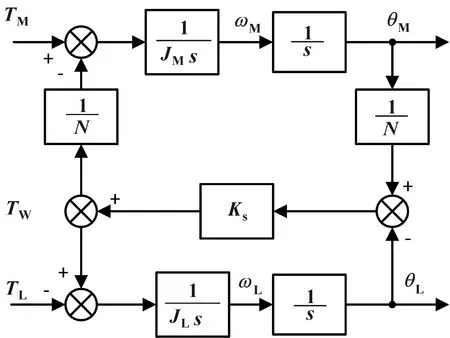
图2 双惯量系统框图Fig.2 Block diagram of the dual inertia system

电磁转矩TM与电机角速度ωM之间的传递函数为

(3)

由公式(3)可看出：双惯量系统传递函数由一个一阶惯性系统和一个二阶振荡系统组成。其中，二阶振荡传递函数中存在一对共轭零点和一对共轭极点，分别对应抗谐振频率点和自然振动频率点。

1.2 柔性关节定位振动分析

通过公式(3)可以求出二阶振荡系统共轭极点对应的自然振动频率ωNTF，以及共轭零点对应的抗谐振频率ωARF：

(4)

(5)

假设某关节电机转子转动惯量JM=0.277×10-4kg·m2，负载侧转动惯量JL=0.1×10-4kg·m2，关节刚度系数Ks=60 N·m/rad，可得到双惯量系统传递函数的伯德图如图3所示。

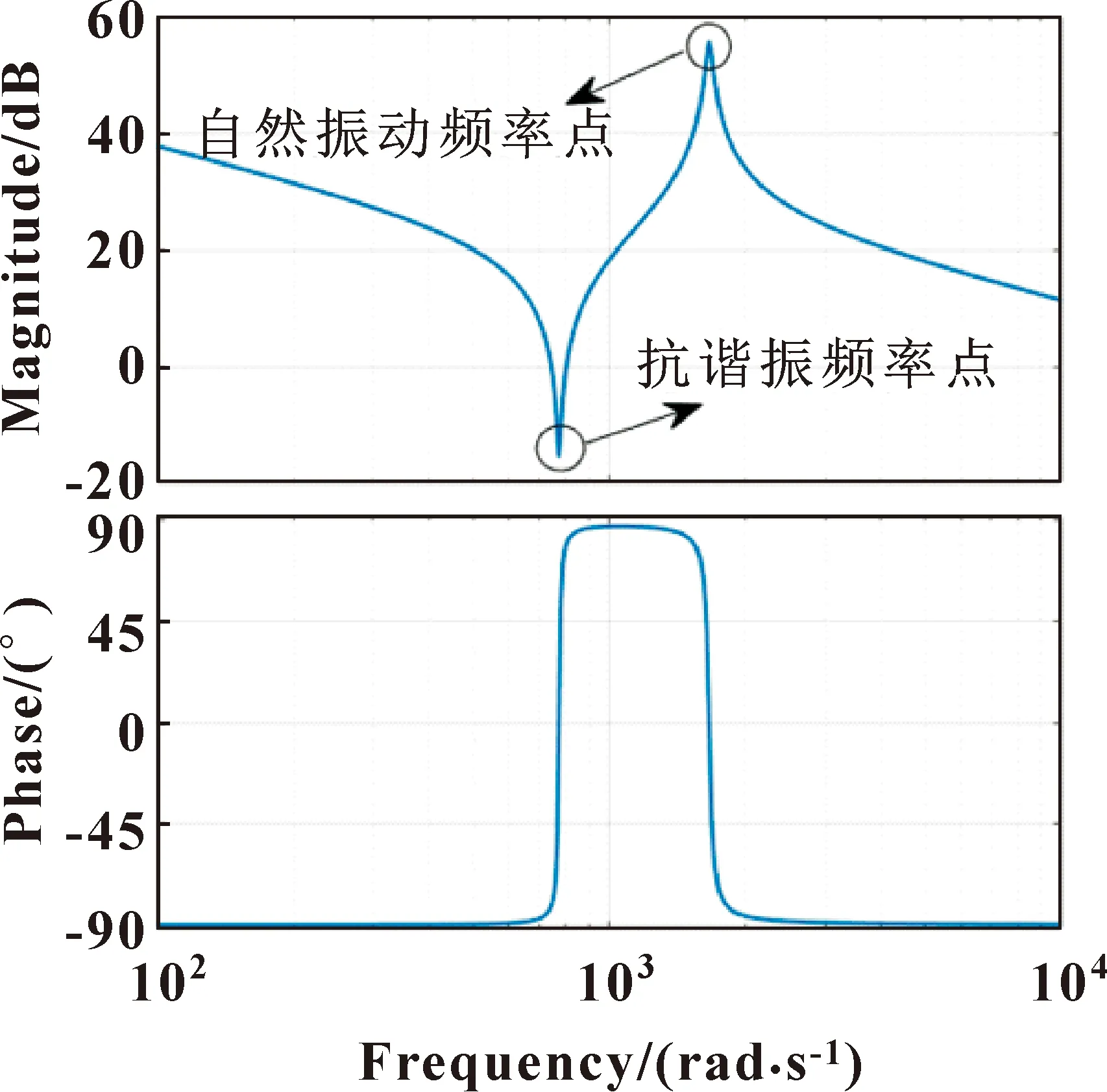
图3 双惯量系统伯德图Fig.3 Bode plots of the double inertia system

由图3可知：在自然频率点处的传递函数幅值增益最大，抗谐振频率点处的传递函数幅增益最小。由于抗谐振频率点导致的幅值增益降低可通过调节伺服系统闭环解决；而自然振动频率点将相位穿越处幅值增益拉高至零分贝以上，导致速度出现振动，即柔性关节出现定位振动现象。

当公式(3)中s=jωNTF时，则在自然振动频率点ωNTF处的幅值增益Mn为

(6)

将式(6)进行简化，可得到：

(7)

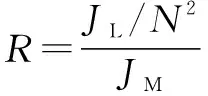
由公式(7)可知：自然振动频率点ωNTF处的幅值增益Mn与系统刚度成反比，系统刚度越大，对应的振动幅值就越小，系统越不容易产生定位振动。在系统发生谐振时，可使用陷波滤波器将参考指令中的谐振分量滤除，使系统在谐振频率处的幅值保持在-3 dB以下，实现振动抑制。

2 滤波器设计及参数确定方法

2.1 滤波器设计

根据柔性关节分析定位振动，在位置闭环前引入陷波滤波器(图4)。将陷波器串联在位置环控制环路之前。其输入信号为上位机输入的位置指令，经过陷波处理后，成为位置环给定输入信号。

传统的陷波滤波器传递函数表达式如公式(8)所示，使控制系统的特征频率偏离双惯量系统的固有频率，实现抑制振动。

(8)

式中：ωn为滤波器中心角频率；ξ1、ξ2分别为陷波深度系数和宽度系数。

由于陷波滤波器在自然角频率点ωn处的幅值增益Dp为

(9)

ξ1和ξ2之间的关系为ξ2=ξ1/10Dp/20，由此可知：宽度系数ξ2与陷波宽度和陷波深度之间存在耦合，不能单独控制陷波宽度和陷波深度。

为此，在传统的陷波滤波器的基础上进行改进，采取极点零点抵消法，即将定位振动的极点放置在陷波滤波器分子上，陷波滤波器分母上的极点替换为阻尼比更高的新极点，如ξ2=1。由滤波器的宽度与阻尼比的关系Bω=ξ2ωn/π，结合式(8)和式(9)得到的改进陷波滤波器传递函数表达式为

(10)

式中：ωn=2πfn为陷波器中心角频率，rad/s；Bω为陷波宽度，Hz；Dp为陷波深度，dB。

传统的陷波滤波器无法单独控制陷波宽度和陷波深度，而改进后的滤波器可以对陷波器中心频率、陷波宽度以及陷波深度进行单独控制，更加简单地设计出满足系统的陷波器。

相较于传统陷波滤波器，图5中改进后的滤波器可以通过ωn、Bω和Dp对滤波器频率、宽度和深度进行单独控制和调整，且ωn、Bω和Dp越大，滤波器频率、宽度和深度越大，可更简单地设计出满足系统定位振动抑制的陷波器。

2.2 参数解耦陷波器参数确定方法

陷波滤波器参数设置对振动抑制效果影响显著，一旦陷波滤波器频率设置偏离振动频率，振动抑制效果将大大减弱，因此需要快速准确地确定滤波器参数。为此，采用下列方法快速整定滤波器ωn、Bω和Dp参数。

(1)陷波器中心频率。对运动控制器采集到的位置跟踪误差进行FFT变换，得到振幅最高点所对应的频率即为陷波滤波器中心角频率ωn。

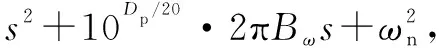
(3)陷波器深度。需要先确定二阶振荡传递函数中的阻尼比系数。阻尼比可采用对数衰减法通过外部测量设备获取到摆动信息计算得知。其中对数衰减率δ为

(11)

式中：Ai表示第i个振动信号的幅值；Ai+j表示第i+j个振动信号的幅值；dj为阻尼比系数；ωn为振动角频率；T为振动周期。

式(11)化简可得：

(12)

又因为

(13)

整理后得到陷波器的深度为

(14)

3 实验与结果

3.1 实验平台与方法

搭建的六自由度工业机器人实验平台如图6所示，工业机器人主要包括：机械臂、减速机、伺服电机、伺服驱动器以及控制器五部分；机器人末端位置信息测试装置激光跟踪仪主要包括：跟踪仪跟踪头、控制箱、主动靶标。

图7所示为实验测试中给定工业机器人末端点路径，对应的轨迹匀速段速度为1 000 mm/s，加速时间1 s的T形加减速曲线。为检测机器人定位振动抑制前后的变化，使用激光跟踪仪以1 000 Hz的采样频率对机器人末端点位置信息进行采样，采样时间为26 s。

3.2 实验结果与分析

通过控制系统对位置跟踪误差进行采样并进行FFT变换，测得各关节振动频率f1-6=(3.2,2.6,2.8,3.1,2.7,3.1)Hz。根据第2.2节滤波参数的确定方法和机器人各关节滤波器参数匹配原则，设置机器人各关节陷波滤波器参数均为振动频率3 Hz，宽度4 Hz，深度3.8 dB。

机器人各关节抑制振动前后FFT频谱图如图8所示，可知：引入滤波器前各关节频谱图含有2个振动频率点，分别在0.5 Hz和3 Hz附近。引入滤波器后，各关节振动中心频率设置点3 Hz处的振幅均得到明显降低，只保留0.5 Hz附近的振动频率点。

为更加直观地验证所提出算法的抑振效果，通过激光跟踪仪对国家标准测试轨迹(图7)下的机器人末端振动信息进行采集，得到工业机器人振动抑制前后机器人末端点轨迹如图9所示。

图9(a)为定位振动抑制前机器人末端实际速度曲线，其匀速段平均速度为1 050.836 7 mm/s，匀速段速度波动范围(841.250 1，1 133.670 8)mm/s，且停止段残余振动明显；图9(b)为振动抑制后的末端实际速度曲线，其匀速段平均速度为998.576 1 mm/s，匀速段速度波动范围(991.489 3，1 054.315 8)mm/s ，并且在停止段没有残余振动。

根据国家标准所规定的实验测试步骤、轨迹速度准确度和轨迹速度波动的计算方法[15]，机器人定位振动抑制前的轨迹速度准确度Av1为5.083 7%，轨迹速度波动vF1为292.420 7 mm/s；定位振动抑制后的轨迹速度准确度Av2为-0.142 39%，轨迹速度波动vF2为62.826 5 mm/s，定位振动得到78.5%的抑制，证明提出的参数解耦陷波滤波器的有效性和参数整定的准确性。

4 结语

针对陷波滤波器在解决六自由度工业机器人伺服系统定位振动问题过程中所面临滤波器参数存在耦合、不便于参数整定的缺点，对柔性关节的双惯量系统进行建模，并分析产生振动的原因和特性。基于零极点抵消法对陷波滤波器改进，实现对陷波器中心频率、陷波宽度以及陷波深度的单独控制。通过将位置跟踪误差进行FFT变换和对数衰减法快速整定陷波器各参数。实验结果表明：参数解耦陷波滤波器不存在参数耦合，参数整定方便；使用参数解耦陷波滤波器后，定位振动得到78.5%的抑制，该方法能够有效抑制定位振动。