一类新的可对角化矩阵及其张量积与张量和
刘慧娟, 秦建国, 王 超
(郑州商学院 通识教育中心,河南 巩义 451200)
0 引言
众所周知,矩阵对角化一直是矩阵论研究的重要课题,而正规矩阵是可对角矩阵。但哪些(类)矩阵属于正规矩阵,人们一直在不停地探索着[1-3]。利用共轭转置矩阵,得到Hermite矩阵,这种矩阵在矩阵论与解析函数插值问题研究中有许多应用[4-8]。受Hermite矩阵和文献[1]的启发,本文找到了一类正规矩阵,即适于条件A*=A2-I的矩阵,并研究了适于这一条件的两个矩阵A,B的张量积与张量和的表达式,给出了适于这一条件的矩阵的张量积、张量和仍是此类型矩阵的充要条件及其行列式的值。
1 基本结论
引理1[4]设A∈Cn×n,则A为正规矩阵当且仅当A酉相似于一个对角矩阵D,而D的对角元素为A的n个特征值λ1,λ2,…,λn。
定理1 设A∈Cn×n,A*=A2-I则
(1)A可以对角化;
(2)A的谱σ(A)是下述集合
的子集;
(3)矩阵属于A不同特征值的特征向量正交;


证明:(1)因为A*=A2-I,以及
A*A=(A2-I)A=A(A2-I)=AA*。
所以A为正规矩阵。由引理1,A可以对角化。
(2)设λ0=a+bi,a,b∈R是A的一个特征值,则有0≠x∈Cn,使
Ax=λ0x。
由于
((A2-I)x,x)=x*((A2-I)x)=(λ02-1)(x,x),

a-bi=(a2-b2-1)+2abi。
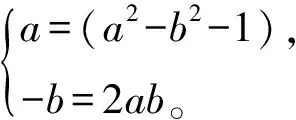
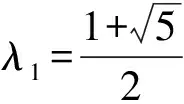
因此,任意此类矩阵的谱σ(A)都是下述集合
的子集。
(3)由定理1,矩阵A是正规矩阵,所以A的属于不同特征值的特征向量正交[4]。
(4)这是由于矩阵A的行列式等于其所有特征值之积。又因为A仅有两个互异的非零特征值,故A非奇异。依据A的逆矩阵的行列式等于A的特征值的倒数之积,便可得|A-1|计算公式。
定理2 设A=(aij),B=(bij)∈Cn×n,A*=A2-I,B*=B2-I,则
(1)(A⊗B)*=(A⊗B)2-(I⊗I)-[(B2⊕A2)-2(I⊗I)],且
(A⊗B)*=(A⊗B)2-(I⊗I)⟺(B2⊕A2)-2(I⊗I)=0;
(2)(A⊕B)*=[(I⊗A)+(B⊗I)]*=(A⊕B)2-(I⊗I)-[2(B⊗A)+(I⊗I)],且
(A⊕B)*=(A⊕B)2-(I⊗I)⟺2(B⊗A)+(I⊗I)=0;
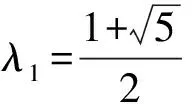

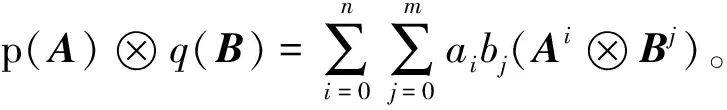
因此 (A⊗B)*=(A⊗B)2-[(A⊗I)2+(I⊗B)2-(I⊗I)]=
(A⊗B)2-(I⊗I)-[(A⊗I)2+(I⊗B)2-2(I⊗I)]=
(A⊗B)2-(I⊗I)-[(B2⊕A2)-2(I⊗I)]。
而且
(A⊗B)*=(A⊗B)2-(I⊗I)⟺(B2⊕A2)-2(I⊗I)=0。
此即,A⊗B与A属于同一类矩阵的充要条件是(B2⊕A2)-2(I⊗I)=0。
(2) (A⊕B)*=[(I⊗A)+(B⊗I)]*=[I⊗(A2-I)]+[(B2-I)⊗I]=
(I⊗A)2+(B⊗I)2-2(I⊗I)=
(I⊗A)2+(B⊗I)2+2(I⊗A)(B⊗I)-2(I⊗A)(B⊗I)-2(I⊗I)=
(A⊕B)2-(I⊗I)-[2(B⊗A)+(I⊗I)]。
而且
(A⊕B)*=(A⊕B)2-(I⊗I)⟺2(B⊗A)+(I⊗I)=0。
此即,A⊕B与A属于同一类矩阵的充要条件是2(B⊗A)+(I⊗I)=0。
(3)由公式|A⊗B|=|A|n|B|n以及tr(A⊗B)=(trA)(trB),经过简单计算可得此二结论。
对于某些适合条件A∈Cn×n及A*=A2-I的矩阵,我们还可以得到一些有趣的结果。

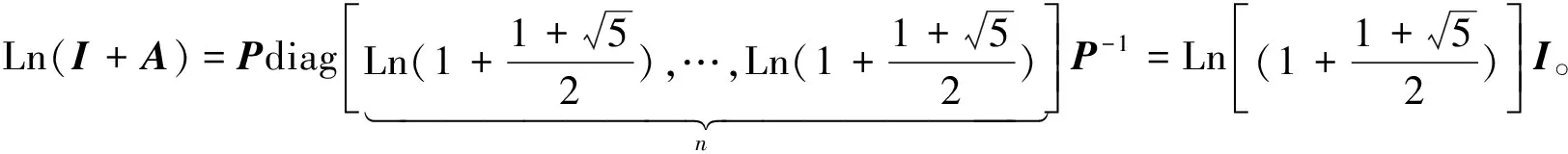
2 结语
本文证明了适于条件A*=A2-I的矩阵A可以对角化,给出了它的谱的范围。讨论了适于条件A*=A2-I的矩阵A及其逆矩阵的行列式,还讨论了两个这类矩阵的张量积与张量和。它还应该有一些其他性质。适合这种条件的矩阵仅有实数特征值,因而它们都是Hermitian矩阵,Hermitian矩阵所具有的良好性质它们都具备。

