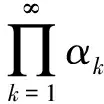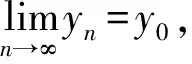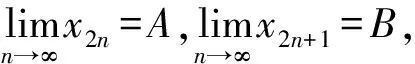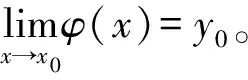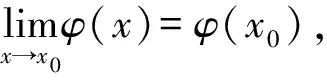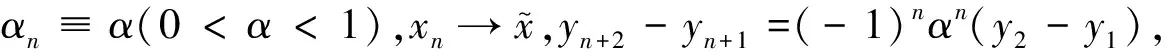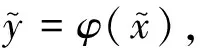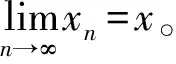关于第十二届全国大学生数学竞赛一道赛题推广的条件
华梦霞, 陈 庆
(南阳师范学院 数学与统计学院,河南 南阳 473061)
数学竞赛活动的开展,可以增强大学生学习数学的兴趣,培养其分析、解决问题的能力,发现和选拔数学创新人才,故不少文献都关注了竞赛试题的研究[1-6]。本文对2020年第十二届全国大学生数学竞赛初赛(数学类A卷)第五题的推广做进一步的研究。 原试题如下:
φ是R上严格单调增加的连续函数,ψ是φ的反函数,实数列{xn}满足
证明{xn}收敛或举例说明{xn}有可能发散。
该试题的答案是可以证明{xn}收敛,文献[1]说明:去掉连续性假设仍可证明{xn}是收敛的。 文献[2]对此进行了推广,得到了如下结果。
命题1φ是R上严格单调函数,ψ是φ的反函数,实数列{xn}满足
xn+2=ψ(αnφ(xn)+(1-αn)φ(xn+1)),
(*)

给出命题1后,文献[2]在αn取一些特殊值时给出了{xn}的极限,但在计算一些具体的{xn}的极限时,仍然假设了φ是连续的。
本文将指出,在命题1基础上计算{xn}的极限时,仍无需假设φ的连续性,可得完全相同的结论。本文主要结果如下。
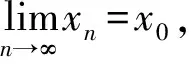
证明:不妨设φ严格单调递增,
xn+2=ψ(αnφ(xn)+(1-αn)φ(xn+1)),
则
φ(xn+2)=αnφ(xn)+(1-αn)φ(xn+1)。
记yn=φ(xn),于是
yn+2=αnyn+(1-αn)yn+1,
由此可知
yn+2-yn+1=-αn(yn+1-yn)。
(1)

(2)
(3)
(4)
(5)
(1)若x1 由(3)(4)(5)三式可知 y1 (6) x1 (7) x2n+1 (8) 由于φ严格单调递增,所以 φ(x2n+1)<φ(B)≤φ(A)<φ(x2n), 即 y2n+1<φ(B)≤φ(A) 令n→∞,y0≤φ(B)≤φ(A)≤y0。所以φ(A)=φ(B)。由于φ严格单调递增,所以A=B,所以{xn}收敛。 因为φ严格单调递增,所以φ在点x0的两个单侧极限均存在,设 (9) 下证a=b=φ(x0)即可。 由于φ严格单调递增,故 b≤φ(x0)≤a。 (10) 由于φ严格单调递增,y2n+1=φ(x2n+1)<φ(x0)<φ(x2n)=y2n。 (2)若x1>x2,采用完全相同的办法,可以证明φ在点x0连续。 若φ严格单调递减,采用类似的方法可以得到结论。 注2:命题2并没有保证φ在R上连续,仅说明:若x1≠x2,{xn}满足(*)式,则φ在{xn}的极限x0连续,若x1=x2,则{xn}为常数列,x1仍可能是φ的间断点。