一种改进基尼指数加权的轴承健康指标构建方法

钱门贵 陈涛 于耀翔 郭亮 高宏力 李威霖

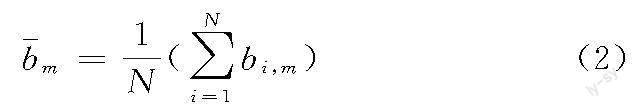
摘要：在轴承的状态监测中，构建一个可以准确描述轴承退化趋势且能及时识别早期退化点（EDP） 的健康指标（HI） 至关重要。目前大多学者提出的健康指标能较好地描述轴承的退化趋势，但不能准确识别早期退化点。提出了一种改进基尼指数（IGI） 加权的轴承健康指标构建方法。利用集成经验模态分解（EEMD） 对原始信号进行分解，根据各分量的故障特征能量比（FCER），对其进行加权重构得到重构信号；计算重构信号的IGI；将IGI作为重构信号的FCER进行加权计算，得到最终的指标IGI-FCER-HI。通过两个实验验证了所提方法的有效性，并与其他健康指标进行了对比。结果表明，所提方法构建的指标不仅具有良好的单调性和趋势性，而且能准确监测轴承的早期退化点。

关键词：滚动轴承；早期退化点；健康指标；集成经验模态分解；加权重构的集成经验模态分解；故障特征能量比；改进的基尼指数

中图分类号：TH133

DOI：10.3969/j.issn.1004-132X.2023.15.006

A Method for Constructing Bearing HIs with IGI Weighting

QIAN Mengui1 CHEN Tao1 YU Yaoxiang1 GUO Liang1 GAO Hongli1 LI Weilin2，3

1.School of Mechanical Engineering，Southwest Jiaotong University，Chengdu，610031

2.Zhejiang Fangyuan Test Group Co.，Ltd.，Hangzhou，310018

3.Key Laboratory of New Energy Automotive Drive Systems for Zhejiang Market Regulation，

Hangzhou，310014

Abstract： In the bearings condition monitoring， it was important to construct a HI that might accurately describe bearings degradation trends and identify EDP. At present， most of HIs proposed might describe the degradation trends of bearings well， but could not accurately identify the EDP. A method for constructing bearing HIs was proposed with IGI weighting. The original signals were decomposed by using EEMD， and the reconstructed signals were weighted according to the FCER of each components. The IGI of the reconstructed signals was calculated.The IGI was weighted as the FCER of the reconstructed signals to obtain the final IGI-FCER-HI. The effectiveness of the method was verified by two experiments. The results show that the IGI-FCER-HI has well monotonicity and trend， may identify EDPs of bearings accurately.

Key words： rolling bearing; early degradation point（EDP）; health indicator（HI）; ensemble empirical mode decomposition（EEMD）; weighted reconstructed EEMD; failure characteristic energy ratio（FCER）; improved Gini index（IGI）

0 引言

滾动轴承是旋转机械的关键部件，滚动轴承的预测和健康管理（prognostics and health management， PHM）是一个重要研究领域［1-3］。相比滚动轴承的故障诊断，如何构建一个可以准确描述轴承退化趋势且及时识别早期退化点（early degradation point， EDP）的健康指标（health indicator， HI） 更为重要。一个好的健康指标不仅可以准确识别轴承当前的运行状况，而且对轴承剩余寿命预测的准确性有较大的提升［4］。

针对滚动轴承的PHM，一般采用各类传感器进行监测分析，如温度传感器和加速度传感器等。但由于温度只对严重的轴承故障敏感，故常见方法是对加速度传感器采集的振动信号进行分析，分析方法主要有以下两种［5-6］：一是根据振动信号采用统计学和信号处理方法进行分析；二是通过机器学习的相关智能方法对振动数据进行训练学习。对于机器学习这类方法，尽管不需要太多的专家知识且容易实现，但是比较依赖数据，更重要的是缺乏可解释性［7-9］。本文重点讨论如何通过统计学和信号处理方法对振动信号提取合适特征并构建健康指标，以实现对轴承的状态监测。

在轴承状态监测中，一般通过信号处理方法从其他异常冲击噪声和谐波干扰中分离出感兴趣的成分，再对其进行时频域分析，从中提取特征以构建能反映轴承退化趋势的健康指标，实现对轴承的状态监测以及寿命预测等工作。在工业中多采用一些时域指标进行轴承的状态监测，而最常用的便是均方根（root mean square， RMS）和峭度指标［2］。LI等［10］将峭度作为寿命预测中的第一次预测点，并用均方根值预测轴承剩余寿命。HUANG等［11］也以均方根值作为预测轴承寿命的特征指标。除了均方根和峭度，很多学者还对其他的时域统计指标进行分析，如均值、方差、标准差、峰值因子、波形因子、偏度、裕度等，而这些指标对轴承的早期退化并不敏感，并不能在强噪信号中取得良好的效果。

时频分析可以改善上述现象，通过对频域的分析，能够获得比时域分析上更多的故障信息。CUI等［12］针对早期故障诊断问题，在时域和频域同时提取特征，避免了使用一个域的局限性。REN等［13］除了从时域中提取三个传统的特征外，另外采用一个新的频域特征进行剩余寿命的预测。顾晓辉等［14］ 应用频域相关峭度定量地刻画窄带信号的包络谱幅值。ZHAO等［15］也基于时频域上提出的周期性调制强度作为轴承的健康指标。YAN等［16］在频谱上利用频谱幅值融合生成的健康指标来检测早期故障。一些学者先对信号进行降噪处理，再提取时频特征作为健康指标。DUONG等［17］采用小波包变换从每个子带中提取健康指标。刘兴教等［18］对振动信号集成经验模态分解（ensemble empirical mode decomposition，EEMD）后的一系列固有模态函数（inherent modal functions， IMFs）进行分析，选用峭度原则重构信号，从重构信号中提取故障特征来评估轴承的健康状况。一些新的健康指标也开始从信息熵的角度被提出，NOMAN等［19］将时频流形和香农熵的概念整合起来构建健康指标。还有一些学者针对轴承故障特征频率，提出一些健康指标的构建方法，如LIM等［20］使用故障频率与周期的加权相关性构建健康指标。上述方法虽然在轴承的早期退化监测方面有所提升，但是趋势性和单调性并不理想，不能准确地反映轴承的整个退化趋势。而针对趋势性和单调性，一些学者提出了稀疏测度（如平滑指数、基尼指数、负熵等）来进行健康指标的构建［21-23］，但是这些指标无法准确检测出轴承的早期退化点且易受冲击噪声的影响。

本文提出了一种改进基尼指数（improved Gini index， IGI）加权的轴承健康指标构建方法。该方法首先运用EEMD将信号分解成一系列的IMFs，利用频谱上故障能量比对IMFs进行加权得到重构信号；然后对重构后的信号进行基于频谱的故障特征能量比（failure characteristic energy ratio， FCER）计算；最后利用IGI对FCER进行重加权得到最终的指标IGI-FCER-HI。采用两个数据集对提出的健康指标进行验证分析，结果显示该指标不仅表现出良好的单调性和趋势性，而且对轴承早期退化敏感可以准确识别早期退化点。

1 基本原理

1.1 集成经验模态分解（EEMD）理论

EEMD是经验模态分解（empirical mode decomposition， EMD）的一种改进算法，实质是以给定的次数对加入高斯白噪声的信号反复应用EMD，对EMD中模态混叠的现象有一定的改善作用。根据文献［24］，EEMD的理论简要过程如下：

（1）对原始信号x（t）中加入随机的高斯白噪声gn（t）：

xm（t）=x（t）+cgn（t）（1）

式中，c为上述高斯白噪声的幅值系数。

（2）通过EMD将信号xm（t）分解成一系列的IMFs。

（3）重复步骤（1）和（2），加入不同的高斯白噪声序列，直至终止条件。

（4）EEMD最终的结果为上述IMFs的平均值，即

式中，N为加高斯白噪声的总次数；bi，m为第i次EMD产生的第m个IMF。

1.2 稀疏测度理论

稀疏测度（例如基尼指数、峭度、负熵、平滑指数等）可以测量信号的稀疏性，量化信号的冲击性，在机械状态检测领域得到了广泛的应用。根据文献［23］对稀疏测度的对比分析，发现基尼指数比其他指标的鲁棒性、稀疏性及循环平稳性更好。基尼指数的计算过程如下。

（1）对于一段信号x［n］，通过带通滤波器［l，h］滤波去除背景噪声得到滤波后的信号xl，h［n］（n=1，2，…，N，其中，N为信号长度）。

（2）对信号xl，h［n］进行希尔伯特变换，得到El，h［n］。

（3）通过下式计算xl，h［n］的平方包络SEl，h［n］ ：

SEl，h［n］=E2l，h［n］（3）

（4）通过下式得到最终的基尼指数：

式中，SEl，h，order［n］为SEl，h［n］的升序序列。

2 所提方法

信号经过EEMD后得到一系列的IMFs，但是受到噪声的影响，往往不容易选取最佳的IMFs。本文根据故障特征频率提出FCER。信号经过EEMD后，根据FCER对所有的IMFs进行加权重构，得到重构后的信号。然后根据基尼指数的特点，对其进行改进并提出IGI。最后计算重构信号的FCER，并将重构信号的IGI作为FCER的权重项，得到最终的IGI-FCER-HI，如图1所示。

2.1 基于加权重构的EEMD预处理算法

由于在复杂工作环境中采集的振动信号必然包含异常冲击和谐波干扰，故需要对信号进行一定的预处理，将无关的信号成分去除。本文采用EEMD进行信号的预处理，但对于信号经过EEMD后，如何去选择最佳的IMFs进行信号的重构至关重要。本文根据轴承故障特征频率提出FCER，用于信号的重构和最终健康指标的构建。具体计算公式如下：

式中，FCE为故障特征能量；g为重力加速度，取9.8 m/s2；FCF為轴承的故障特征频率，包括4种故障频率（外圈、内圈、保持架和滚动体）；E（FCF）为包络谱上在FCF处的幅值；k为谐波数，一般取4～8，本文取7；E（f）为包络谱上前k倍FCF的幅值总和。

根据EEMD得到m个IMFs，计算每个IMF的FCER，记作fi；然后对FCER进行归一化处理：

最后将上述结果作为权重，对所有的IMFs进行加权重构，得到预处理后的重构信号xre：

图2所示为基于加权重构的EEMD预处理算法流程。

2.2 改进基尼指数加权的健康指标构建

就传统的稀疏测度而言，在状态检测领域依然存在一些缺点：①易受冲击的干扰，波动性较大，难以准确检测到早期故障；②在整体退化趋势上，很难表现出较好的单调性。由于稀疏测度中的基尼指数性能较为优越，故本文针对稀疏测度中的基尼指数进行改进并构建健康指标。

根据式（4） 的基尼指数计算，对其中的SEl，h［n］进行改进，提出ISE，其具体公式如下：

式中，C为正常数，本文按照式（11） 取值；varh为健康状态下轴承振动信号的方差；a为一百分比参数，一般大于15%，本文取60%。

根据式（4），提出IGI的计算公式：

考虑到FCER对早期故障较为敏感，且不易受冲击和谐波的干扰，而IGI在整体的退化趋势上有较好的单调性和趋势性，故将IGI作为FCER的权重项，从而提出最终构建的健康指标IGI-FCER-HI公式：

IGI-FCER-HI=IGI·FCER（13）

3 实验验证

为了验证所提方法的有效性，对两组轴承全寿命周期的实验进行分析。

3.1 实验一

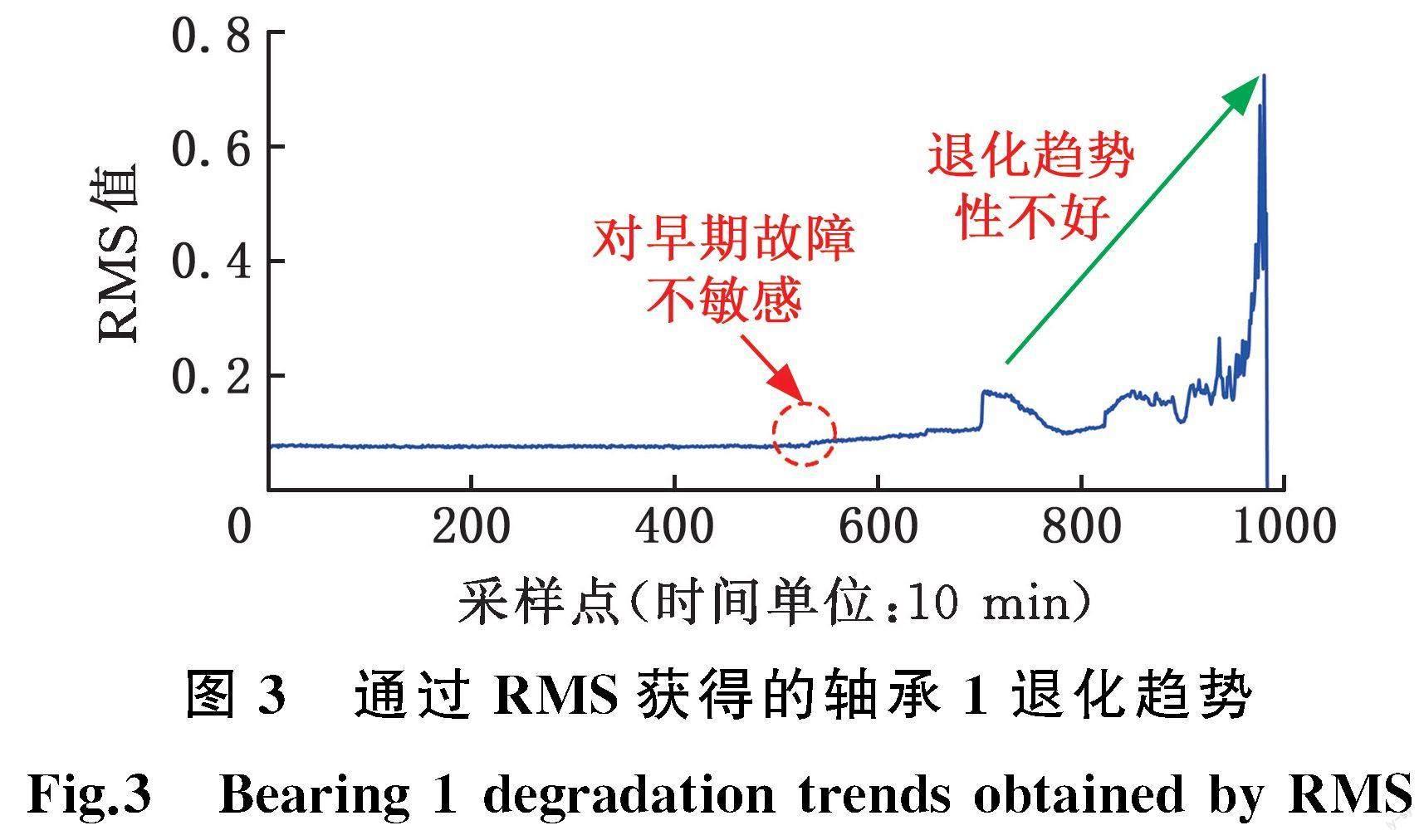
该实验采用的是IMS的全寿命周期数据集，该数据集已经被许多学者广泛研究，故本文首先采用该数据集验证所提方法 ［1］。该实验将4个双列轴承安装在转速为2000 r/min的轴上，并通过弹簧机构向轴和轴承施加约2.72 t（6000磅）的径向载荷以进行加速寿命实验。实验每10 min收集一次数据，采样频率为20 kHz，每次采样信号长度为20 480。该组实验进行了164 h，直到轴承失效，最终发现轴承1故障类型为外圈故障。根据轴承的具体参数，计算出其外圈、内圈、滚动体和保持架的故障特征频率，分别为236.43 Hz、296.90 Hz、14.78 Hz和140.04 Hz。图3给出该组数据轴承1的RMS值，可以看出通过RMS获得的退化曲线虽然比较平稳，波动性不大，但是EDP难以检测到。

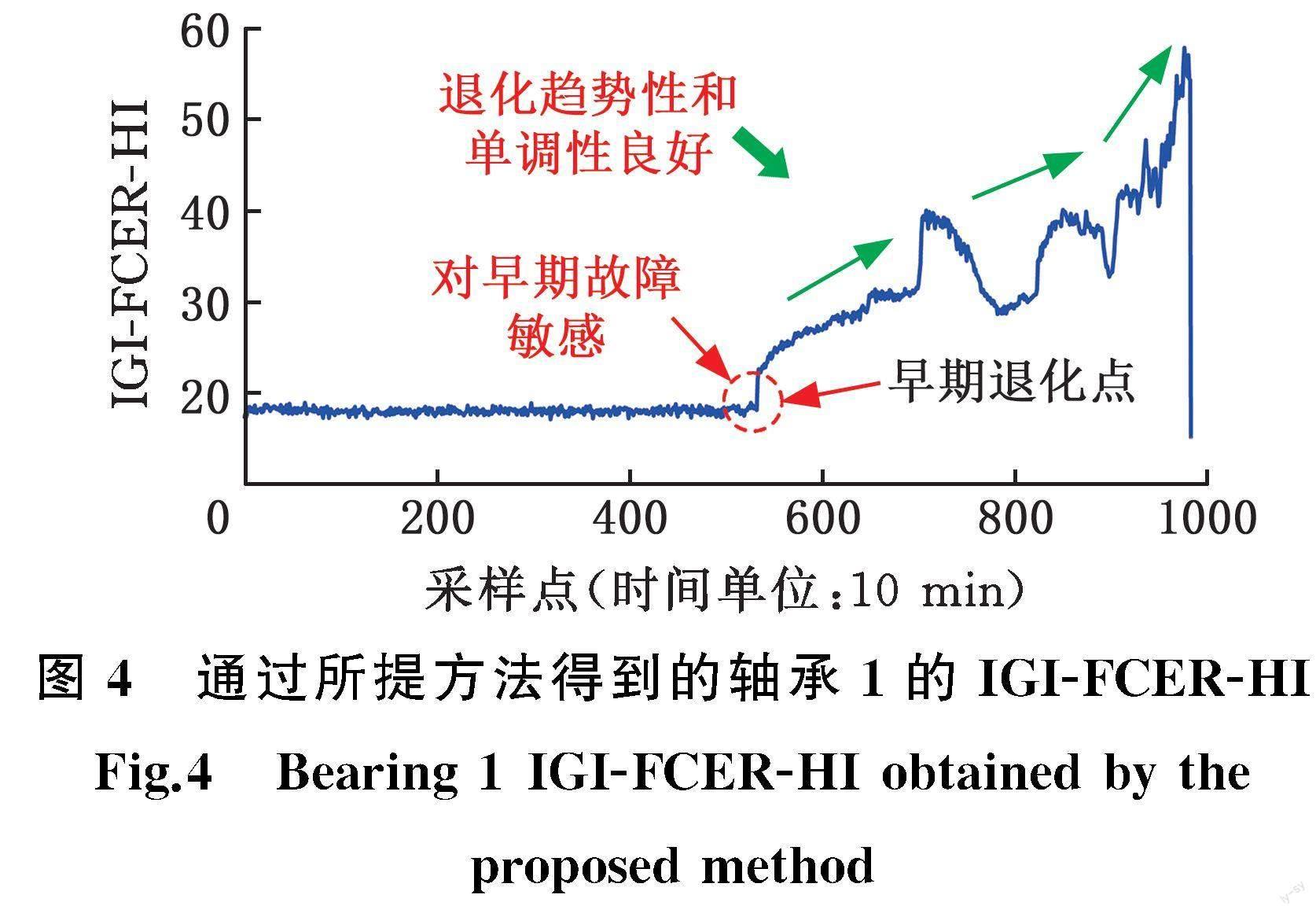
对该组数据应用本文方法，对于式（11） 中健康状态下轴承振动信号的方差varh取整个数据前10%的平均值，得到最终的IGI-FCER-HI，如图4所示。可以看出，整体的波动性不大，在早期退化点位置指标有较大的变化，能够准确及时地监测到早期故障。随着轴承的退化，IGI-FCER-HI也表现出良好的趋势性和单调性。

为了说明本文所提IGI-FCER-HI性能的优越性，根据文献［22］提出的基于自适应加权信号预处理技术的一些稀疏测度构建的健康指标，选取峭度（kurtosis）、平滑指数（smoothing index）、负熵测度（negative entropy） 和基尼指數（Gini index） 进行对比。图5所示为这4个测度应用于该组数据的结果。可以发现这些健康指标对轴承的退化并不敏感，在早期退化点处变化幅度并不明显。为了量化比较本文构建的健康指标和其他健康指标的趋势性Mon和单调性Tre，分别给出其计算公式：

式中，HIS为所求趋势性的健康指标序列；Dpos、Dneg分别为HIS对时间求导时导数值大于0和导数值小于0的数量；h为HIS总的序列（观测）数量；xk为观测时期k的健康指标值；tk为观测时期k对应的时间值。

针对早期退化点判断的准确性，本文提出早期退化点敏感性指标SenEDP，并且定义其计算公式如下：

式中，XEDP+1、XEDP分别为HIS在早期退化点后一观测点和早期退化点时期的对应值；a为HIS前（EDP-1）观测点的方差。

由上式可知，SenEDP越大，证明对应的健康指标对早期故障越敏感，对早期退化点的判断越准确。由大量学者分析和本文构建的IGI-FCER-HI可知，IMS该组数据的早期退化点为第533个采样点。

计算IGI-FCER-HI指标和其他指标的上述三个性质，见表1。为了更好地对比不同指标的性能差异，作图6所示的柱状对比图，可以发现本文提出的健康指标不仅保留了良好的单调性和趋势性，而且在早期故障监测方面表现优越，从而验证了所提方法的有效性。

3.2 实验二

为了进一步验证所提方法的通用性和有效性，使用另外一组轴承全寿命周期实验数据进行分析。实验二采用XJTU-SY滚动轴承加速寿命试验数据集，轴承试验台如图7所示，被测轴承型号为LDK UER204［25］。对15个轴承进行测试，在三种不同的工况下进行加速退化实验。振动信号每1 min采集一次，每次采集时间为1.28 s，采样频率为25.6 kHz。

由于工况3数据较长，故本文对工况1和2中选取的三个轴承1-3、1-5和2-2数据进行分析。由于篇幅所限，仅给出这三组数据应用所提方法所得结果，如图8所示。

计算1-3、1-5和2-2三组数据对应指标的单调性、趋势性和早期退化点敏感性，见表2～表4。同理，为了更好地进行对比分析，对三组数据进行综合评价，作出三组数据各指标平均值的柱状图，结果如图9所示。可以发现本文方法构建的IGI-FCER-HI相对其他指标性能依旧有所提升。

3.3 尺度相似性分析

在实际的工业场景中，为了更好地对轴承更好地进行状态监测，对构建的健康指标制定一个合适的阈值非常关键。即在阈值以下，轴承处于健康状态；超过一定阈值后，轴承发生故障。这就要求所构建的健康指标在不同工况下应具有良好的尺度相似性，即健康指标的最小值和最大值应具有相似的尺度，且在退化趋势上应尽可能一致。两个轴承健康指标的尺度相似性的计算公式如下：

式中，h（1）max、h（2）max分别为轴承1和2的健康指标最大值；h（1）min、h（2）min分别为轴承1和2的健康指标最小值；L（h（1））、L（h（2））分别为轴承1和2的健康指标幅值长度，指标在0～1之间，越接近1，说明尺度相似性越大。

通过上述两组实验的结果，对本文所构建的健康指标尺度相似性进行分析。轴承处于健康状态时，健康指标均在20以下；而在轴承最终失效时，健康指标均达到60左右。计算上述4个轴承健康指标相互的尺度相似性，见表5。尺度相似性均在0.9左右，由于两组实验的工况和轴承型号均不相同，所以构建的健康指标具有良好的尺度相似性，对于工业实际应用具有较大的参考价值。

4 结论

（1）由于EEMD分解后难以选择合适的IMFs，故本文从故障频率本身出发，提出FCER对IMFs进行加权重构，有效提高了EEMD提取故障信息的能力和效率。

（2）针对健康指标的趋势性和单调性与准确监测早期故障难以两全的问题，提出IGI加权的健康指标，在保证趋势性和单调性的同时，大大提高了轴承早期故障监测的能力。

（3）通过两组不同的实验，验证了提出的IGI-FCER-HI指标具有良好的尺度相似性，在工程实际应用领域具有较大的参考价值。

参考文献：

［1］ QIU H， LEE J， LIN J， et al. Wavelet Filter-based Weak Signature Detection Method and Its Application on Rolling Element Bearing Prognostics［J］. Journal of Sound and Vibration， 2006， 289（4/5）：1066-1090.

［2］ WANG D， TSUI K L， MIAO Q. Prognostics and Health Management：a Review of Vibration Based Bearing and Gear Health Indicators［J］. IEEE Access， 2017， 6：665-676.

［3］ GUO L， LI N， JIA F， et al. A Recurrent Neural Network Based Health Indicator for Remaining Useful Life Prediction of Bearings［J］. Neurocomputing， 2017， 240：98-109.

［4］ LEI Y， LI N， GUO L， et al. Machinery Health Prognostics：a Systematic Review from Data Acquisition to RUL Prediction［J］. Mechanical Systems and Signal Processing， 2018， 104：799-834.

［5］ 张淑清，李威，张立国，等.基于多元经验模态分解互近似熵及GG聚类的轴承故障诊断［J］. 中国机械工程， 2016， 27（24）：3362-3367.

ZHANG Shuqing， LI Wei， ZHANG Liguo，et al. Bearing Fault Diagnosis Based on Multi-EMD， cApEn and GG Clustering Algorithm［J］. China Mechanical Engineering， 2016， 27（24）：3362-3367.

［6］ ZHAO M， LIN J. Health Assessment of Rotating Machinery Using a Rotary Encoder［J］. IEEE Transactions on Industrial Electronics， 2017， 65（3）：2548-2556.

［7］ GUO L， LEI Y， LI N， et al. Machinery Health Indicator Construction Based on Convolutional Neural Networks Considering Trend Burr［J］. Neurocomputing， 2018， 292：142-150.

［8］ GUO L， LEI Y， LI N， et al. Machinery Health Indicator Construction Based on Convolutional Neural Networks Considering Trend Burr［J］. Neurocomputing， 2018， 292：142-150.

［9］ 何強， 唐向红， 李传江，等. 负载不平衡下小样本数据的轴承故障诊断［J］.中国机械工程， 2021， 32（10）：1164-1171.

HE Qiang， TANG Xianghong， LI Chuanjiang， et al. Bearing Fault Diagnosis Method Based on Small Sample Data under Unbalanced Loads［J］. China Mechanical Engineering， 2021， 32（10）：1164-1171.

［10］ LI N， LEI Y， LIN J， et al. An Improved Exponential Model for Predicting Remaining Useful Life of Rolling Element Bearings［J］. IEEE Transactions on Industrial Electronics， 2015， 62（12）：7762-7773.

［11］ HUANG Z， XU Z， KE X， et al. Remaining Useful Life Prediction for an Adaptive Skew-Wiener Process Model［J］. Mechanical Systems and Signal Processing， 2017， 87：294-306.

［12］ CUI H， QIAO Y， YIN Y， et al. An Investigation of Rolling Bearing Early Diagnosis Based on High-frequency Characteristics and Self-adaptive Wavelet De-noising［J］. Neurocomputing， 2016， 216：649-656.

［13］ REN L， CUI J， SUN Y， et al. Multi-bearing Remaining Useful Life Collaborative Prediction：a Deep Learning Approach［J］. Journal of Manufacturing Systems， 2017， 43：248-256.

［14］ 顧晓辉，杨绍普，刘永强，等. 一种改进的峭度图方法及其在复杂干扰下轴承故障诊断中的应用［J］. 振动与冲击， 2017， 36（23）：187-193.

GU Xiaohui， YANG Shaopu， LIU Yongqiang， et al. An Improved Kurtogram Method and Its Application in Fault Diagnosis of Rolling Element Bearings under Complex Interferences［J］. Journal of Vibration and Shock， 2017， 36（23）：187-193.

［15］ ZHAO M， JIA X. A Novel Strategy for Signal Denoising Using Reweighted SVD and Its Applications to Weak Fault Feature Enhancement of Rotating Machinery［J］. Mechanical Systems and Signal Processing， 2017， 94：129-147.

［16］ YAN T， WANG D， XIA T， et al. A Generic Framework for Degradation Modeling Based on Fusion of Spectrum Amplitudes［J］. IEEE Transactions on Automation Science and Engineering， 2022，19（1）：308-319.

［17］ DUONG B P， KHAN S A， SHON D， et al. A Reliable Health Indicator for Fault Prognosis of Bearings［J］. Sensors， 2018， 18（11）：3740.

［18］ 刘兴教，赵学智，李伟光，等. 基于峭度原则的EEMD-MCKD的柔性薄壁轴承故障特征提取［J］. 振动与冲击， 2021， 40（1）：157-164.

LIU Xingjiao， ZHAO Xuezhi， LI Weiguang， et al. EEMD-MCKD Fault Feature Extraction Method for Flexible Thin-wall Bearing Based on Kurtosis Principle［J］. Journal of Vibration and Shock， 2021， 40（1）：157-164.

［19］ NOMAN K， HE Q， PENG Z， et al. A Scale Independent Flexible Bearing Health Monitoring Index Based on Time Frequency Manifold Energy & Entropy［J］. Measurement Science and Technology， 2020， 31（11）：114003.

［20］ LIM C， KIM S， SEO Y H， et al. Feature Extraction for Bearing Prognostics Using Weighted Correlation of Fault Frequencies over Cycles［J］. Structural Health Monitoring， 2020， 19（6）：1808-1820.

［21］ MIAO Y， ZHAO M， LIN J. Improvement of Kurtosis-guided-grams via Gini Index for Bearing Fault Feature Identification［J］. Measurement Science and Technology， 2017， 28（12）：125001.

［22］ HOU B， WANG D， WANG Y， et al. Adaptive Weighted Signal Preprocessing Technique for Machine Health Monitoring［J］. IEEE Transactions on Instrumentation and Measurement， 2020， 70：1-11.

［23］ HOU B， WANG D， YAN T， et al. A Comparison of Machine Health Indicators Based on the Impulsiveness of Vibration Signals［J］. Acoustics Australia， 2021， 49（2）：199-206.

［24］ LEI Y， HE Z， ZI Y. Application of the EEMD Method to Rotor Fault Diagnosis of Rotating Machinery［J］. Mechanical Systems and Signal Processing， 2009， 23（4）：1327-1338.

［25］ WANG B， LEI Y， LI N， et al. A Hybrid Prognostics Approach for Estimating Remaining Useful Life of Rolling Element Bearings［J］. IEEE Transactions on Reliability， 2018， 69（1）：401-412.