基于二阶近似扩展卡尔曼滤波的锂离子电池SOC估计

段林超 张旭刚 张华 宋华伟 敖秀奕

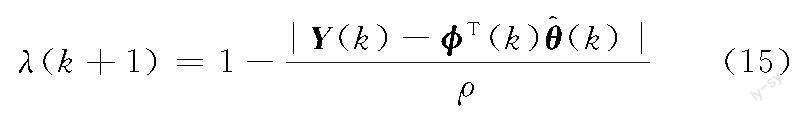
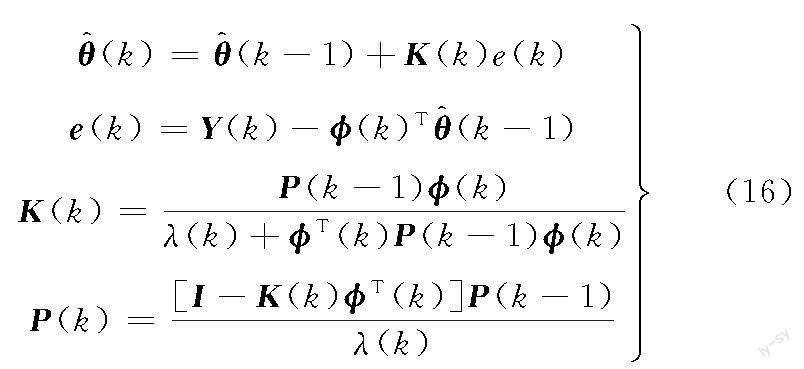
摘要：为提高电池荷电状态（SOC）估计的准确性，更高阶的扩展卡尔曼滤波（EKF）算法被用来估计SOC值。首先建立锂离子电池一阶Thevenin等效电路模型，采用样条函数来表述开路电压（OCV）和SOC值的函数关系。为更加精确地识别等效电路模型参数，提出一种新的带有可变遗忘因子最小二乘法（VFFRLS）的算法来在线识别模型参数。由于VFFRLS解的精度依赖于算法初始值的设定，为此采用改进粒子群算法求得模型初始参数值，进而得到更加精确的VFFRLS初始值。最后采用二阶EKF来估计电池的SOC值，以此提高估计精度。两组不同的数据集用来证明二阶EKF估计SOC值具有普适性。实验结果表明，二阶EKF在估计不同工况条件下的SOC值时，平均绝对误差（MAE）都保持在1%以内，由此证明了所提方法的有效性。

关键词：电池荷电状态；二阶扩展卡尔曼滤波；可变遗忘因子最小二乘法；改进粒子群算法；参数识别

中图分类号：TM911.3

DOI：10.3969/j.issn.1004-132X.2023.15.004

SOC Estimation of Lithium-ion Batterys Based on Second-order Approximation Extended Kalman Filter

DUAN Linchao1，2 ZHANG Xugang1，2 ZHANG Hua1，2 SONG Huawei3 AO Xiuyi3

1.Key Laboratory of Metallurgical Equipment and Control Technology，Ministry of Education，Wuhan University of Science and Technology，Wuhan，430081

2.Hubei Key Laboratory of Mechanical Transmission and Manufacturing Engineering，Wuhan University of Science and Technology，Wuhan，430081

3.Recycling of Scrapped Vehicles （Including New Energy Vehicles） Hubei Engineering Research Center，Wuhan，430014

Abstract： To improve the accuracy of battery SOC estimation， a higher order EKF algorithm was used to estimate SOC. Firstly， the first-order Thevenin equivalent circuit model（ECM） of lithium-ion battery was established， and the function relationship between open circuit voltage（OCV） and SOC was expressed by spline function. In order to more accurately identify the ECM parameters， a new kind of with VFFRLS algorithm was proposed for on-line identification of model parameters. Since the accuracy of the VFFRLS solution depended on the setting of the initial values of the algorithm， the improved particle swarm optimization algorithm was used to obtain the initial parameters of ECM， which helped to obtain more accurate initial values of VFFRLS. Finally， the second-order EKF was employed to estimate the SOC of the batterys to improve the estimation accuracy. Two different datasets were used to demonstrate the universality of second-order EKF estimation SOC. The experimental results indicate that the mean absolute error（MAE） of second-order EKF is within 1% when estimating SOC under different working conditions， which proves the effectiveness of the proposed method.

Key words： state of charge（SOC）； second-order extended Kalman filter（EKF）； variable forgetting factor recursive least square（VFFRLS）； improved particle swarm optimization； parameter identification

0 引言

鋰电池目前已被广泛地应用在消费产品中，具有低成本和较高的能量密度等优点［1］。锂电池具有快速充电和放电能力，且工作过程中有着较高的稳定性，因此被广泛应用于能源的储存和供应不同的设备，尤其是电动汽车［2］。电池电荷状态（state of charge，SOC）是电池管理系统中的关键参数之一，反映了电池单体内部的状态且不能够被直接测量得到，但实时了解该状态量可保证电池管理系统做出正确的决策［3］。目前，用来估计SOC的方法有多种：放电测试法［4］、开路电压法［5］、安时积分法［6］、神经网络方法［7］和模型估计法［8］等。放电测试法一般用于实验室环境中，不适应于实际工程环境；开路电压法则需要长时间静置，耗时严重；安时积分法估计精度依赖于初值的设定且误差也会在积分过程中累加，从而导致估计误差增大；神经网络方法虽然估计精度较高，但其估计精度依赖于数据集的大小和精度，且计算量较大。

由于模型法在估计SOC值时有着较高的精度和较小的计算量，故模型法在估计SOC值中被更为广泛地应用在实际工况中［9］。卡尔曼滤波算法被用来对目标值进行估计，还有粒子滤波［10］和H无穷滤波算法等［11］。由于卡尔曼滤波算法只能应用于线性系统，而基于电池模型所得到状态和测量方程为非线性方程，故需要采用扩展卡尔曼滤波器（extended Kalman filter，EKF）来对SOC值进行估计。EKF的原理是将状态方程和测量方程中的非线性方程通过一阶Taylor展开，将其近似为线性方程［12-14］。由于该近似将二阶及二阶以上项忽略，使得模型误差增大，从而导致估计值误差偏大。

利用EKF来估计SOC值的重要前提就是得到模型的参数，且模型参数精确性直接影响后续SOC估计的结果，因此准确得到电池模型参数是必要的。文献［15-16］采样的方法是带有遗忘因子的最小二乘法来识别模型参数，但该方法中遗忘因子的值为恒定常数，并不能根据误差等信息进行及时的调整，因此存在一定的不足，且最小二乘法解精度在一定程度上依赖于算法初始值的设定，更为合理的初始参数值尤为重要。文献［17］采用的是离线的参数识别的方法，主要是通过对数据进行函数拟合，从而得到函数的系数，进而得到模型参数，但该方法只能用于离线的识别，不能进行实时的参数识别，且工况一旦发生改变，模型参数也会跟随改变，这无疑会使得估计得到的参数误差增大。

为解决一阶Taylor近似误差偏大问题，同时防止后续计算量偏大，本文采用二阶Taylor展开从而得到近似线性化模型，然后利用EKF完成对SOC的滤波估计。根据最小二乘法估计误差绝对值，本文提出一种可根据误差值绝对值大小实时调节遗忘因子大小的最小二乘法来在线识别电池模型参数，由此提高识别参数精度。同时本文采用改进粒子群算法求得电池模型初始参数值，由此获取最小二乘法中较为准确的初始参数值来提高解的精度。最后通过實验对比EKF和二阶EKF估计SOC误差值的大小来验证本文方法的有效性。

1 锂离子电池模型

电池内部的化学反应十分复杂，即使相同的锂电池在相同的条件下所表现出的性能也可能会有所差异［18］。不同的电池模型有着不同的优点和缺点，目前，等效电路模型和电化学模型被广泛地应用于电荷状态的估计。电化学模型使用电化学方法来描述动力电池的工作情况，从计算的角度来看其计算较为复杂。等效电路模型被广泛用来描述动力电池内部动态特征和静态特征，并且有着较高的精度，该方法要比电化学方法更为简单且计算量较小［19］。

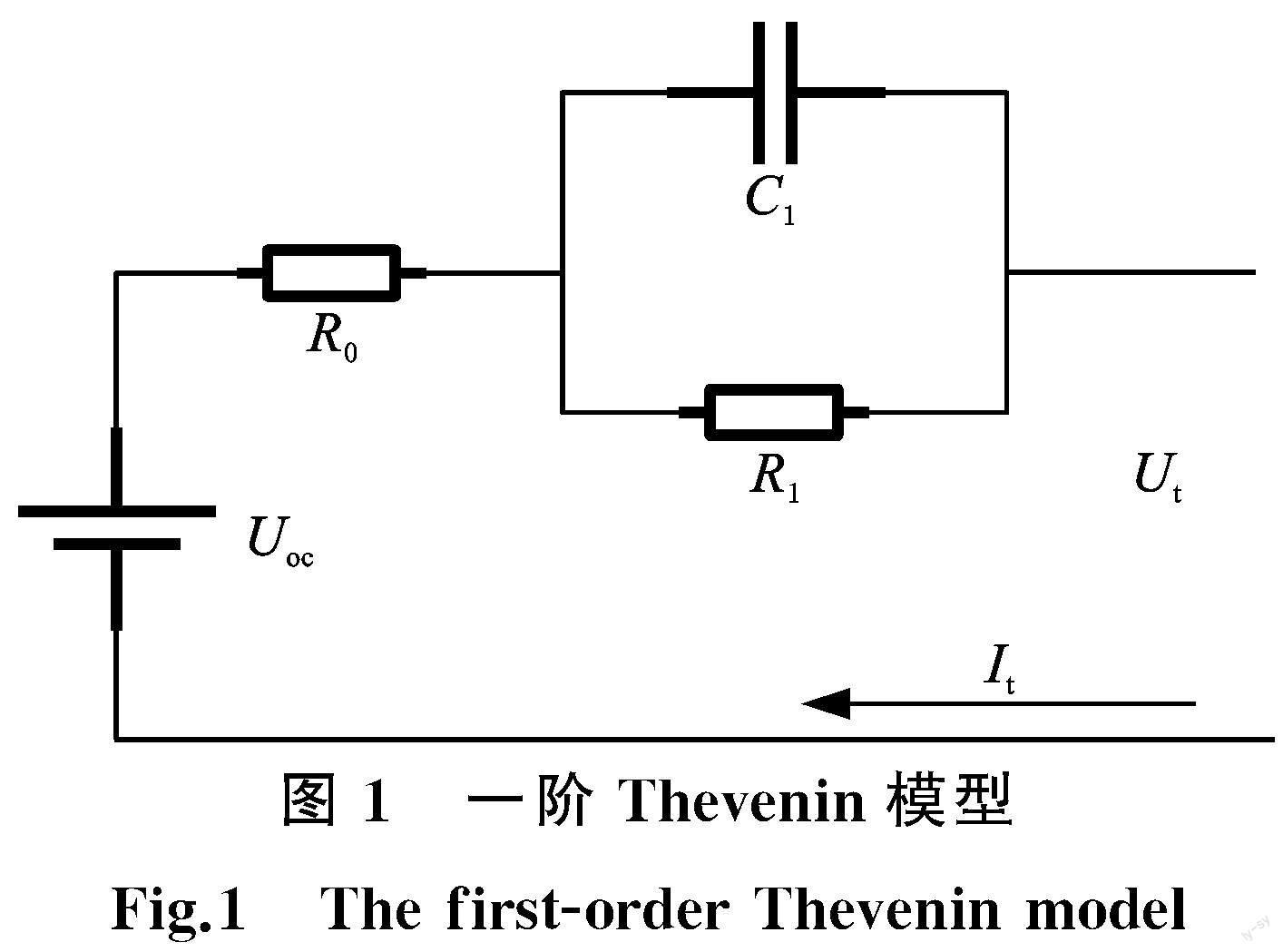
电池模型不仅要反映出其动态特性，同时也应具有简单和计算方便等特征，因此本文采用一阶Thevenin电路模型［20］，如图1所示。

图1中，Uoc为开路电压，Ut为端电压，R0为电池内部电阻，C1为极化电容，R1为极化电阻。根据基尔霍夫电压定律，可得

式中，It为负载电流；U1为极化电压。

电荷状态（SOC）值的计算公式如下：

其中，S（t0）、S（t）分别代表t0时刻和任意时刻SOC值；Qn为电池实际容量；η为库仑效率，显然上式都是关于时间的函数，为连续函数。现将上式进行离散化，得到所对应离散化方程：

式中，ik-1为k-1时刻的电流值。

其中，Ts和Δt取值均为1。根据上述离散方程可得到电池模型状态方程和测量方程：

其中，Uoc，k为SOC值的函数，本文用样条函数来表达其函数关系式。将式（5）、式（6）表示为矩阵形式：

其中，uk=Ik，ωk、υk分别为过程噪声和测量噪声。

2 改进的可变遗忘因子最小二乘法电池模型参数识别

电池模型参数识别主要有在线识别和离线识别两种方法。在实际工况条件下其模型参数不断发生改变，因此离线的参数识别不可避免地会产生一定误差［21］。本文采用最小二乘法（recursive least square，RLS）来在线识别Thevenin模型参数。首先定义系统传递函数：

其中，由离散化传递函数可得其差分方程：

Y（k）=E（k）－U（k）=

－a1Y（k－1）+a2I（k）+a3I（k－1）（10）

其中，Y（k）、I（k）分别为系统输出和输入。整理可得

对比式（12）和式（8）系数可得

利用最小二乘法求出a1、a2、a3三个参数，即可得到电池模型各个参数值。由于带有定常数遗忘因子的最小二乘法在时变系统中并不能提供良好的表现，故本文提出一种根据误差和误差增量关系来实时调整遗忘因子参数值的方法。现定义误差增量Δek如下：

Δek=ek－ek－1（14）

ek=Y（k）－（k）Tθ^（k-1）

利用误差ek和误差增量Δek的乘积构成一个特征变量，用于判断遗忘因子是否需要调整。当ΔekΔek<0时，即表明系统误差绝对值朝着误差减小的方向发展，此时的遗忘因子大小满足要求，即在下次迭代过程中，遗忘因子参数值保持不变。当ΔekΔek>0时，表现为系统误差绝对值朝着误差增大的方向发展，应及时通过迭代的方法调整遗忘因子参数值，以保持算法具有良好的追踪能力和收敛性，其迭代步骤如下：

其中，ρ为缩放因子，用来帮助调节λ的取值范围。最小二乘法迭代步骤如下：

带有遗忘因子λ（k）的RLS的迭代步骤如图2所示。

由于RLS求解精度受限于a1、a2、a3三个参数的设定，当初值参数值设定更加接近真实值时，算法求解精度较高且收敛速度较快，但当初始参数值设定与真实值相差较大时，解的精度会降低甚至算法会发散，因此，本文采用改进粒子群算法先求解电池模型初始参数，进而得到更为合理的初值，以提高解的精度值。

标准粒子群算法容易陷入局部最优解，从而导致解的误差偏大。为此本文采用非线性动态惯性权重系数ω来增强全局搜索能力［22］，其表达式如下：

其中，f、favg、fmin分别为粒子适应度值、适应度值平均值和最小值。由式（1）得到粒子群算法目标函数：

其中，U^（k）为模拟端电压，U（k）为实际端电压，N为数据长度。求出初始模型参数，进而得到RLS初始参数值。

3 二阶扩展卡尔曼滤波算法

由于本文研究对象的状态方程为线性方程，故只给出测量方程二阶Taylor展开的推导过程。将式（7）中非线性函数g（·）在状态估计值处展开成为泰勒级数：

测量方程可转化为

其中，ny表示测量向量维数；ei表示第i个ny维基向量，则预测方程为

由于状态方程为线性方程，故状态向量的一步预测和误差协方差矩阵的一步预测Pk|k-1与标准EKF算法步骤一致，二阶EKF滤波增益矩阵迭代步骤如下：

Lk=Pk|k－1CkH－1k（22）

其中，Ck为函数g（·）的雅可比矩阵，Hk的计算方法如下：

综上所述，二阶EKF算法步骤见表1。其中，Q、R分别代表过程噪声矩阵和测量噪声矩阵。

4 验证和讨论

4.1 电池模型参数识别结果

由于锂离子电池具有能量密度高和自放电率小等诸多优点［23］，故锂离子电池被作为本文的研究对象，分别采用NASA公开数据集［24］和马里兰大学的Center for Advanced Life Cycle Engineering（CALCE）公开数据集作为实验数据，可以从文献［14］中获取CALCE数据集的详细信息。根据两个不同的数据集建立对应的等效电路模型，结合式（18）构造出对应的目标函数，利用粒子群算法求得电池模型初始参数值，见表2。

本文采用样条函数来表达SOC值和OCV值的函数关系。现定义样条函数定义域，由于SOC值的变化范围为［0，1］，故自然样条函数定义域为［0，1］，那么n段样条函数可以表述为

其中，0=s0

ξ（s）=ais3+bis2+cis+di（25）

将测试点作为样条函数节点，由节点处函数值、一阶、二阶导数值都应连续和边界条件作为约束，求出上式中的待定系数［25］，即可求出各个区间内SOC-OCV函数表达式。部分区间内SOC-OCV函数关系式的系数见表3。

通过上述步骤即可求出SOC值和开路电压的函数关系，为后续识别特定工况下电池模型参数打下良好的基础。NASA和CALCE数据中所对应不同工况的电流和端电压如图3所示，实验温度均为25 ℃。

利用本文所提出的VFFRLS算法识别模型参数，参数识别结果和模拟端电压误差如图4所示。端电压误差如图4d所示，可以看出误差都在0附近波动。其中，NASA数据中模拟端电压的平均误差为0.0021 V；而对于CALCE，端电压的平均误差仅为0.0011 V。由此可以证明，本文提出的VEERLS算法识别出的参数有较高的精确度。

4.2 基于二阶EKF的SOC估计

为证明本文所提出的二阶EKF估计SOC有着更高的精度，以EKF估计得到的SOC值作为对比实验来辅助验证本文所提方法的优越性。其中，NASA数据集中初始SOC值为1，而CALCE数据中的初始SOC值为0.8。图5a和图6a所示为算法估计得到的SOC值。图5b和图6b所示为算法估计SOC值的误差值。从误差曲线中可以看出，二阶EKF在估计不同工况条件下的误差都小于EKF。为了更加直观地对比各个算法在估计SOC的精度，表4给出了不同算法所对应的最大误差（MAX），平均绝对误差（mean absolute error，MAE）和均方根误差（root mean square error，RMSE）。可以看出，二阶EKF在估计NASA数据集中的SOC值时，算法的MAE值为0.0017，远小于EKF的MAE值。另外，二阶EKF在估计CALCE数据集内的SOC值时，算法对应的RMSE值和MAE值都小于EKF的相应值。

4.3 初始SOC值对算法估计的影响

SOC的初始值对二阶EKF算法估计精度有着重要的影响。图7a和图8a所示为不同SOC初值条件下，算法对SOC值的估计结果。由图7b可以看到，虽然二阶EKF在估计SOC值初始阶段所对应的误差稍大于EKF的相应值，但随着算法的运行，二阶EKF误差的收敛性要高于EKF，且更加接近于0。图8b表明，二阶EKF相较于EKF有着更快的收敛速度。结合图7b和图8b的SOC值估计误差曲线可知，初始SOC值在算法估计的初始阶段有较大的影响，但随着算法的运行，初始值的影响逐渐减弱。在实验过程中，为了获取精确的初始SOC值，可以先将电池完全放电，再按照电池所要求的标准充电模式将电池充满，然后进行后续的研究，以此来减小由于SOC初始值不精确所带来的影响。

5 结论

扩展卡尔曼滤波EKF被广泛应用于电池荷电状态SOC值估计中，但在进行Taylor展開近似时，往往只进行一阶近似，这会增大估计误差。为此，本文采用二阶Taylor展开，近似得到线性化模型来估计SOC值。同时采用样条函数来表达SOC值和开路电压OCV值的函数关系，并采用带有可变遗忘因子的最小二乘法（VFFRLS）来在线识别等效电路模型参数。经过实验验证，得到以下结论：

（1）采用样条函数来表示SOC值和OCV值函数关系比较合理，为后续参数识别和SOC值的估计提供精确开路电压值。

（2）首先利用改进粒子群算法得到VFFRLS法的初始值，再采用VFFRLS法在线识别等效电路模型参数，识别得到的模型参数具有较高的准确性。

（3）两个不同的数据集被用来证明二阶EKF的普适性。实验结果表明，二阶EKF估计不同工况条件下的SOC值时，算法所对应的MAE值和RMSE值均小于EKF的相应值，由此证明了本文方法的有效性。

参考文献：

［1］ ZHOU R， ZHU R， HUANG C G， et al. State of Health Estimation for Fast-charging Lithium-ion Battery Based on Incremental Capacity Analysis［J］. Journal of Energy Storage， 2022， 51：104560.

［2］ YANG J， CAI Y， MI C. Lithium-ion Battery Capacity Estimation Based on Battery Surface Temperature Change under Constant-current Charge Scenario［J］. Energy， 2022， 241：122879.

［3］ SHEN J， MA W， XIONG J， et al. Alternative Combined Co-estimation of State of Charge and Capacity for Lithium-ion Batteries in Wide Temperature Scope［J］. Energy， 2022， 244：123236.

［4］ OUYANG T， XU P， CHEN J， et al. Improved Parameters Identification and State of Charge Estimation for Lithium-ion Battery with Real-time Optimal Forgetting Factor［J］. Electrochimica Acta， 2020， 353：136576.

［5］ XING Y， HE W， PECHT M， et al. State of Charge Estimation of Lithium-ion Batteries Using the Open-circuit Voltage at Various Ambient Temperatures［J］. Applied Energy， 2014， 113：106-115.

［6］ MOHAMMADI F. Lithium-ion Battery State-of-Charge Estimation Based on an Improved Coulomb-Counting Algorithm and Uncertainty Evaluation［J］. Journal of Energy Storage， 2022， 48：104061.

［7］ HU C， MA L， GUO S， et al. Deep Learning Enabled State-of-charge Estimation of LiFePO4 Batteries：a Systematic Validation on State-of-the-art Charging Protocols［J］. Energy， 2022， 246：123404.

［8］ JIN Y， ZHAO W， LI Z， et al. SOC Estimation of Lithium-ion Battery Considering the Influence of Discharge Rate［J］. Energy Reports， 2021， 7：1436-1446.

［9］ WANG D， ZHANG Q， HUANG H， et al. An Electrochemical-thermal Model of Lithium-ion Battery and State of Health Estimation［J］. Journal of Energy Storage， 2022， 47：103528.

［10］ YE M， GUO H， CAO B. A Model-based Adaptive State of Charge Estimator for a Lithium-ion Battery Using an Improved Adaptive Particle Filter［J］. Applied Energy， 2017， 190：740-748.

［11］ XIONG R， YU Q， WANG L， et al. A Novel Method to Obtain the Open Circuit Voltage for the State of Charge of Lithium-ion Batteries in Electric Vehicles by Using H infinity Filter［J］. Applied Energy， 2017， 207：346-353.

［12］ 李偉， 刘伟嵬， 邓业林. 基于扩展卡尔曼滤波的锂离子电池荷电状态估计［J］. 中国机械工程， 2020， 31（3）：321-327.

LI Wei， LIU Weiwei， DENG Yelin. SOC Estimation for Lithium-ion Batteries Based on EKF［J］. China Mechanical Engineering， 2020， 31（3）：321-327.

［13］ LI X， WANG Z， ZHANG L. Co-estimation of Capacity and State-of-charge for Lithium-ion Batteries in Electric Vehicles［J］. Energy， 2019， 174：33-44.

［14］ SHI N， CHEN Z， NIU M， et al. State-of-charge Estimation for the Lithium-ion Battery Based on Adaptive Extended Kalman Filter Using Improved Parameter Identification［J］. Journal of Energy Storage， 2022， 45：103518.

［15］ SUN D， YU X， WANG C， et al. State of Charge Estimation for Lithium-ion Battery Based on an Intelligent Adaptive Extended Kalman Filter with Improved Noise Estimator［J］. Energy， 2021， 214：119025.

［16］ FU S， LIU W， LUO W， et al. State of Charge Estimation of Lithium-ion Phosphate Battery Based on Weighted Multi-innovation Cubature KalmanFilter［J］. Journal of Energy Storage， 2022， 50：104175.

［17］ JI Y， QIU S， LI G. Simulation of Second-order RC Equivalent Circuit Model of Lithium Battery Based on Variable Resistance and Capacitance［J］. Journal of Central South University， 2020， 27（9）：2606-2613.

［18］ SUN F， XIONG R. A Novel Dual-scale Cell State-of-charge Estimation Approach for Series-connected Battery Pack Used in Electric Vehicles［J］. Journal of Power Sources， 2015， 274：582-594.

［19］ LIU W， PLACKE T， CHAU K T. Overview of Batteries and Battery Management for Electric Vehicles［J］. Energy Reports， 2022， 8：4058-4084.

［20］ 劉征宇， 黎盼春， 朱诚诚， 等. 基于组合模型的锂电池参数辨识和电池荷电状态在线联合估计［J］. 中国机械工程， 2020， 31（10）：1162-1168.

LIU Zhengyu， LI Panchun， ZHU Chengcheng， et al. Lithium Battery Parameter Identification and SOC Online Joint Estimation Based on Combined Model［J］. China Mechanical Engineering， 2020， 31（10）：1162-1168.

［21］ LIU Y， HUANG Z， WU Y， et al. An Online Hybrid Estimation Method for Core Temperature of Lithium-ion Battery with Model Noise Compensation［J］. Applied Energy， 2022， 327：120037.

［22］ 董文永， 康岚兰， 刘宇航， 等. 带自适应精英扰动及惯性权重的反向粒子群优化算法［J］. 通信学报， 2016， 37（12）：1-10.

DONG Wenyong， KANG Lanlan， LIU Yuhang， et al. Opposition-based Particle Swarm Optimizationwith Adaptive Elite Mutation and Nonlinear Inertia Weight［J］. Joumal on Communications， 2016， 37（12）：1-10.

［23］ TIAN Y， LAI R， LI X， et al. A Combined Method for State-of-charge Estimation for Lithium-ion Batteries Using a Long Short-term Memory Network and an Adaptive Cubature Kalman Filter［J］. Applied Energy， 2020， 265：114789.

［24］ XU Z， WANG J， LUND P D， et al. Co-estimating the State of Charge and Health of Lithium Batteries through Combining a Minimalist Electrochemical Model and an Equivalent Circuit Model［J］. Energy， 2022， 240：122815.

［25］ WU D， ZHANG T， ZHONG Y， et al. Analytical Shaping Method for Low-thrust Rendezvous Trajectory Using Cubic Spline Functions［J］. Acta Astronautica， 2022， 193：511-520.