变构型飞行器柔性蒙皮形状光纤重构方法

王元锋 祝连庆 何彦霖 周康鹏

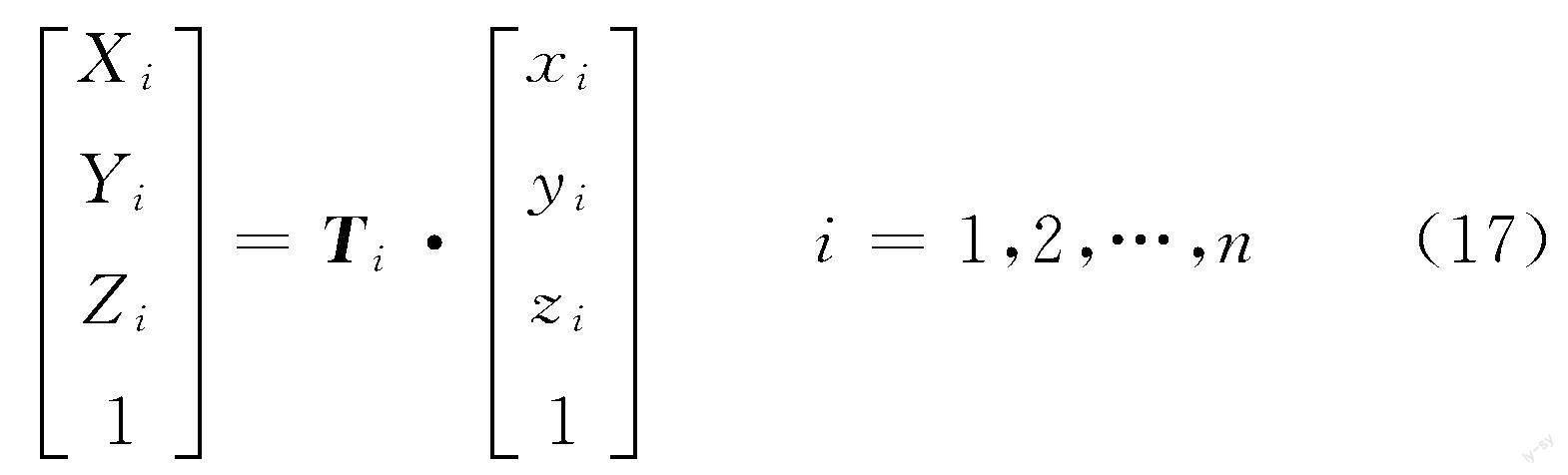
摘要：變构型飞行器在飞行过程的大尺度变形监测是航空航天领域的研究难点和热点，现有方法难以实现飞行器飞行过程中的高精度三维变形监测。针对这一问题，提出一种基于光纤传感的变构型飞行器柔性蒙皮形状光纤重构方法，以实现飞行器飞行过程中的变形监测。基于光纤光栅应变传感原理，推导了光纤应变和曲率之间的关系，建立了光纤传感局部坐标系和全局坐标系之间的转换矩阵，实现了光纤测点坐标到全局坐标系的转换，根据空间曲线拟合方法研究了基于曲线拟合的三维变形重构算法。同时，为了减小光纤传感器的测量误差，对光纤传感器进行标定测试，获得了传感器的应变灵敏度。为了验证所提方法的有效性，对柔性蒙皮样件在不同曲率下的三维变形重构进行了实验测试。实验结果表明，柔性蒙皮样件在0～15.38 m-1曲率的变形范围内，形状重构方法的平均误差为3.5%，最小误差不足2.1%。所提方法在航空航天等领域具有较好的应用前景。

关键词：多芯光纤光栅；三维变形；柔性蒙皮；飞行器；重构算法

中图分类号：TG83

DOI：10.3969/j.issn.1004-132X.2023.15.012

Flexible Skin-shaped Optical Fiber Reconstruction Method for Allomorphic Aircrafts

WANG Yuanfeng1，2 ZHU Lianqing1，2 HE Yanlin1，2 ZHOU Kangpeng2，3

1.School of Instrument Science and Opto-Electronics Engineering，Beijing Information Science & Technology University，Beijing，100192

2.Beijing Laboratory of Optical Fiber Sensing and System，Beijing Information Science & Technology University，Beijing，100192

3.School of Precision Instrument and Opto-Electronics Engineering，Tianjin University，Tianjin，300072

Abstract： Large-scale deformation monitoring of allomorphic aircrafts in the flight processes was a research difficulty and hot spot in the aerospace field， and the existing methods were difficult to achieve high-precision three-dimensional deformation monitoring during the flight of the aircrafts. Aiming at this problem， a flexible skin-shaped fiber reconstruction method for a variant aircraft was proposed based on optical fiber sensing to achieve deformation monitoring during flight of the aircrafts. Based on the principle of fiber grating strain sensing， the relationship between fiber strain and curvature was derived， the conversion matrix between the local coordinate system and the global coordinate system of optical fiber sensing was established， the conversion of fiber measurement point coordinates to the global coordinate system was realized， and the three-dimensional deformation reconstruction algorithm was studied based on curve fitting according to the spatial curve fitting method. At the same time， in order to reduce the measurement errors of the fiber optic sensors， the calibration tests of the fiber optic sensors were carried out to obtain the strain sensitivity of the sensors. In order to verify the effectiveness of the proposed method， the three-dimensional deformation reconstruction of flexible skin samples under different curvatures was tested experimentally. Experimental results show that the average error of the shape reconstruction method is as 3.5% and the minimum error is less than 2.1% in the deformation ranges of 0～15.38 m-1 curvature of flexible skin samples. The proposed method has a good application prospect in aerospace and other fields.

Key words： multicore fiber grating； three-dimensional deformation； flexible skin； aircraft； refactoring algorithm

0 引言

变构型高超声速飞行器是一种大空域、超高速、长距离、高精度的新型飞行器，具有多维大尺度自适应变形的能力，它集航空航天、材料、气动控制等多学科交叉研究领域于一体，是近年来最重要的前沿技术之一［1-3］。与以往常规的飞行器相比，超高声速飞行器具有通过变形来改善飞行器气动性能的能力，同时面临着更为恶劣的飞行力学环境和热环境，因此这种飞行器对稳定性有着更高的要求。通过对航天器进行变形监测能够及时获得结构的形态特征，从而对其飞行姿态进行有效控制［3-5］，增强飞行器的飞行性能。

变构型飞行器相比于普通飞行器，不仅要求蒙皮质量要小、刚度要大、可以承受并传递气动载荷，而且要求具有足够的光滑连续性和大尺度变形特性，以满足飞行器的变形需求。由于材料的大尺度变形特性，这种材料对形态感知器件的性能要求是比较高的。目前用于大型柔性结构的变形监测方法（如摄像法、三维坐标法等）存在测量困难、过程复杂、精度低等局限［4-7］，不适用于高速飞行器的实时监测。与传统方法相比，光纤布拉格光栅（fiber bragg grating，FBG）具有独特的优势，极大减小了尺寸和质量，简化了安装，并且抗电磁干扰，能够在恶劣工况下工作。这种技术允许数百个弱反射光纤布拉格光栅传感器沿一根光纤进行空间分布，使得光纤光栅传感器易于组成分布式测量网络，大大节省了成本，具有直接监测变形表面形状的巨大潜力，特别适合航空航天领域的应用，被广泛用于航空航天飞行器的健康监测领域。

国外学者在光纤光栅传感监测大型飞行器方面开展了研究。DVORAK 等［8］将 FBG传感器布设于无人机机翼中，并通过地面静态测试验证了该方法检测机翼应力分布的有效性，但未对机翼的形变进行研究。KRESSEL等［9］在一架印度曙光无人机（Nishant UAV）上布设FBG多路复用传感网络进行载荷监测飞行试验，以评估光纤监测技术在飞机结构健康监测中的适用性。NICOLAS等［10］通过在碳纤维复合材料机翼表面布设 FBG 传感网络，对机翼施加静态集中载荷和分布载荷，获得机翼的形状和表面载荷分布，与传统的应变片相比，FBG可以承受更大的应变强度。CIMINELLO 等［11］通过 FBG 传感器检测翼梁的形变，从而评估其疲劳状态，并提出一种基于短时傅里叶变换的结构响应信号分析方法，最后通过静态和动态变形实验验证了该方法的有效性。WADA等［12］以一架中型喷气式客机为试验机，对基于OFDR-FBG的分布式光纤传感监测技术进行了飞行验证。WADA等［13］又采用类似的飞行试验方案验证了OFDR-FBG分布式光纤传感技术应用于中型喷气客机机翼应变监测的技术可行性，但未对机翼进行变形重构。

国内学者也对此展开了深入的研究。王寅等［14］提出了一种用于柔性无人机机翼形变监测的方法，通过在翼梁上布设 FBG测得应变数据，结合Ko位移理论获得无人机机翼弯曲、扭转等参数信息，但未进行重构。袁慎芳等［15］在梁式机翼的翼梁结构上布设FBG传感器，结合Ko位移理论实现应变-位移变换，最终对机翼的变形进行重构，平均误差为5%。张科等［16］利用逆有限元法对变形机翼鱼骨进行变形重构，机翼末端重构误差不超过1.73 cm。WANG等［17］针对四边形弹性薄板大扰度变形进行重构，重构的平均误差为4.9%。上述研究为飞行器变形监测的应用奠定了基础，但是目前针对飞行器大尺度变形的重构精度比较低。

本文提出了一种基于多芯光纤的飞行器柔性蒙皮三维变形重构方法。通过研究光纤应变传感方法，建立了光纤传感应变和曲率之间的关系，研究了基于空间曲线拟合的飞行器三维变形重构方法，同时对传感器的应变灵敏度进行了标定，并对柔性蒙皮样件在不同曲率下的变形进行了实验测试和误差分析。

1 影像检测系统的构成及其工作原理

1.1 影像检测系统的硬件构成

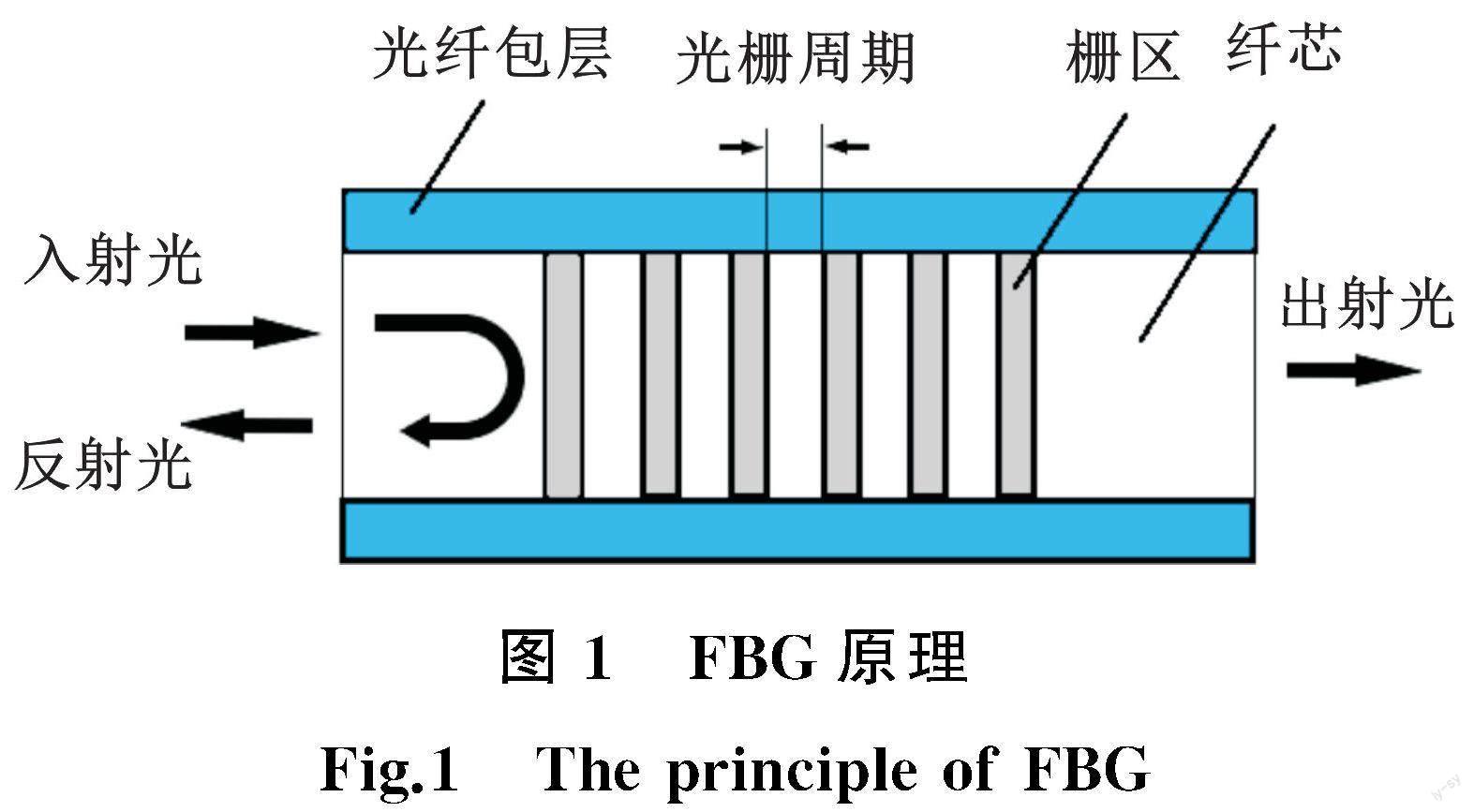
对于光纤入射光线，符合Bragg条件的光将被反射，不满足条件的光则会透射，如图1所示。其中，Bragg条件为

λB=2neffΛ（1）

其中，λB为FBG反射光的中心波长；neff为有效折射率；Λ为光栅周期。当neff和Λ发生变化时，光纤的中心波长也会发生变化［18］。

当被测结构发生形变产生应变时，粘贴在表面的FBG传感器也发生相应的形变，从而引起了光纤中心波长的漂移，即

ΔλB/λB=（1－Pe）ε（2）

式中，ΔλB為反射光中心波长漂移量；ε为轴向应变；Pe为有效弹光系数［18-20］。

当FBG固定在超弹性材料上进行应变测量时，材料发生变形，光栅随之发生变形弯曲，产生波长漂移，如图2所示。

取曲面上的一段微元进行分析，微元段厚度为h，长度为L，微元段上下表面伸缩量为ΔL，m为中性面到上表面的距离，φ表示圆心角，ρ表示曲率半径［18］。

当受到应力时，微元上下表面产生了2ΔL的差值，上下表面之间存在一层长度不变的中性面，如图2中虚线位置所示。对于等厚度平板结构，m近似为h/2，由此可以得到轴向应变

1.2 空间坐标计算

飞行器蒙皮的变形重构实际上是研究空间曲面的重构方法。对三维空间的曲面进行重构，需要确定实现重构的算法，本文采用的基于坐标变换的三维曲面可视化重构的实现过程主要包括获取曲率信息、离散曲率的连续化、进行变形曲线的拟合、利用插值完成曲面拟合并且通过MATLAB平台实现重构。

本文采用四纤芯光纤光栅，配合算法对曲面进行重构。假设光纤在变形的时候，忽略扭转的影响，只考虑光纤发生的轴向弯曲，则光纤的应变与旁轴纤芯到中性轴之间距离的关系为

其中，k为曲率；ρ为曲率半径；δ为旁轴纤芯到中性轴的距离。示意图见图3。

纤芯a与中性轴的夹角为φ，可以用来表示曲率的弯曲方向；旁轴纤芯a、b、c之间的夹角βa、βb、βc均为120°，ra、rb、rc为旁轴纤芯到中间纤芯的距离［19］，且ra、rb、rc相等。在任意位置的三个纤芯的应变方程组可以表示为

由上式可以推导出曲率k：

引入运动坐标系的概念，光纤发生纯弯曲变形时，测点指向下一个测点的切线方向为ZN轴正方向，与曲率k重合的方向为XN的方向，则根据右手螺旋定则判断YN轴正方向，YN轴在中性轴上。坐标系如图4所示。

假设第i点曲率大小为ki，且ki≠0时，曲率半径大小为ρi，曲率方向与Xi轴正方向夹角为φi，已知两个点之间弧线段长度为ds，每段圆弧对应的圆心角可以表示为

θi=ds/ρi（7）

记点i+1在Oi坐标系下的坐标为{xi+1，yi+1，zi+1}，可以推算出点i+1坐标的表达式［18-22］：

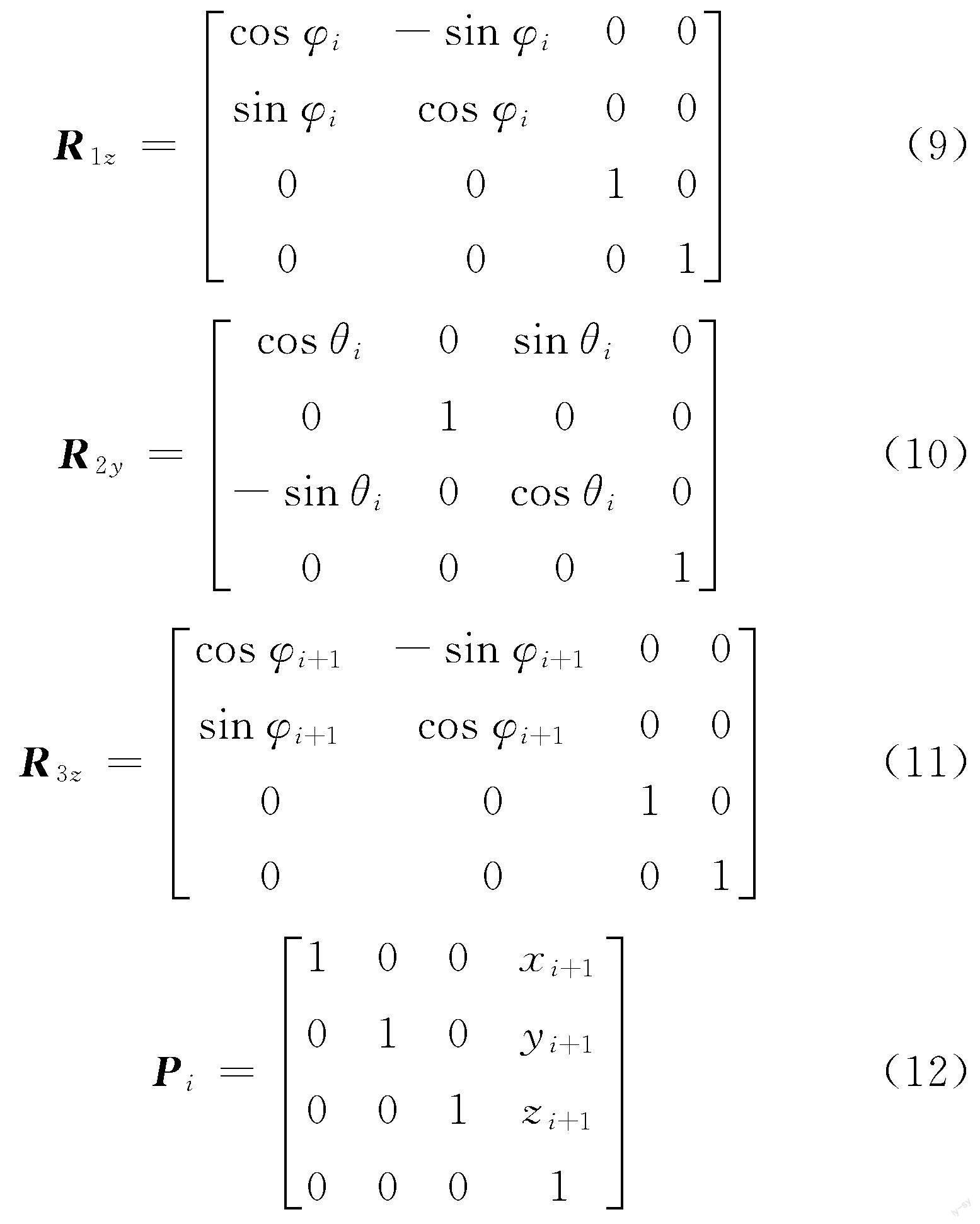
三维空间上相邻坐标之间存在转换关系，定义三维坐标旋转过程表达式为（x，y，z）→（x，y，z，φ）→（x′，y′，z′），其中，（x，y，z）表示旋转前的坐标轴；（x，y，z，φ）表示绕x轴，由y轴旋转到z轴，旋转角度为φ，其中φ有正负号，根据右手螺旋定则判断，逆时针旋转则φ为正，反之为负；（x′，y′，z′）表示旋转后的坐标轴。平移表达式为（x，y，z）→（tx，ty，tz）→（x′，y′，z′），其中tx、ty、tz分别表示沿x、y、z轴平移的距离。Oi与Oi+1坐标系之间的变换矩阵为

由此可以得到Oi坐标系转换到Oi+1坐标系的表达式：

ti+1=PiR3zR2yR1z（13）

从Oi+1坐标系转换到Oi坐标系的表达式为

Oi=t－1i+1·Oi+1i=0，1，…，n－1（14）

从Oi节点坐标系转换到O0坐标系的递推矩阵为Ti，即

O0=Ti·Oii=1，2，…，n（15）

因此，Ti与ti+1的关系为

Ti+1=Ti·t－1i+1i=1，2，…，n－1（16）

其中，T1为单位矩阵。因此，空间中全部点在O0节点坐标系下的坐标为

至此，i（i=1，2，…，n）个离散空间坐标系中曲线段的点坐标依次换算到O0节点坐标系中。

节点坐标系与全局坐标系之间存在转化关系，坐标系转换目的是求全部点在全局坐标系下的坐标。节点坐标系与全局坐标系之间的转换矩阵为

基于上述过程，可以将空间全部点坐标转移到全局坐标系下，从而进行空间曲线拟合重构，实现曲线和曲面的重构。

2 光纤光栅传感器标定

为了保证实验测量精度，需对传感器的应变灵敏度进行标定。实验中制备多芯光纤传感器的材料为中国长飞公司商用多芯光纤MCF 7-42/150/250（SM），共有7个纤芯，由1个中间纤芯和6个呈六角形几何分布的旁轴纤芯组成，光纤包层直径为150 μm，每个纤芯直径为8.1 μm，纤芯间距为41.5 μm。光纤旁轴纤芯分布均匀，空间排布紧凑，光纤各个纤芯的材料以及几何结构均相同，具有相似的轴向应变灵敏度和温度灵敏度。

本文设计的应变灵敏度标定试验系统（图5）由蒙皮试样、位移平台、解调仪和上位机组成。应变传递效率测量实验中蒙皮两端水平固定在高精度位移台上，通过在位移平台施加一定的预紧力使蒙皮试样保持绷直状态。位移平台保持固定，通过旋钮施加水平方向的位移产生不同的伸长量。传感器连接解调仪和上位机来采集传感器的中心波长漂移量。实验所用的蒙皮试样如图6所示，以变构型飞行器柔性蒙皮为研究对象，制作尺寸为200 mm×50 mm×0.2 mm的柔性蒙皮试样，材质为牛津布。将多芯光纤传感器通过环氧树脂固定在试样表面，封装好的传感器共8个测点。

应变ε表示光纤产生的变形量与光纤原始长度的比值，即ε=ΔL/L。实验设定位移平台左右两端间隔200 mm，每拉伸一次水平方向平移 0.1 mm，所对应的应变量步进为500 με，按光纤长度变化量计算出相应的应变量，最大应变量为5000 με。当多芯光纤传感器拉伸加载至最大应变量时，进行去载实验使光纤传感器的拉伸量逐级去载到初始状态，每完成一组应变加载去载实验为一次，该标定实验重复3次。通过光谱仪采集各纤芯上FBG传感点的光谱信号，计算出相应的中心波长偏移量。

记录实验中8个测点的多芯光纤纤芯应变灵敏度，见表1，得到应变灵敏度平均值分别是0.84、0.85、0.86、0.86、0.86、0.86、0.87和 0.84（单位均为pm/με），应变灵敏度实验测量均方差为0.01 pm/με，平均线性度为0.992，经过3次实验重复测量后传感器应变灵敏度的均方差为0.01 pm/με，结果表明传感器具有良好的应变灵敏度，可满足实验要求。

3 实验测试及结果分析

3.1 实验系统的建立

为验证本文重构方法在不同曲率变形下的有效性，设计并搭建了柔性蒙皮三维变形重构实验平台，如图7所示。该系统由曲率块、蒙皮实验件、FBG传感器、扇入扇出装置、FBG解调仪及上位机组成。

实验采用的柔性蒙皮大小为160 mm×50 mm×0.24 mm，弹性模量为3.59 GPa，泊松比为0.3。蒙皮附着在不同曲率的曲率块上，曲率块曲率半径分别为100 mm、80 mm、65 mm，对应曲率K分别为10 m-1、12.5 m-1、15.38 m-1。蒙皮上布设有两根七芯光纤光栅传感器，传感器总长度160 mm、单根上设有8个传感点，每个测点栅区长度为10 mm、栅间距为10 mm。

扇入扇出模块实现空分信道复用和解复用功能，可在-30～90 ℃条件下工作。解调仪根据光纤输出信號进行解调。LabView软件测量和记录蒙皮表面的多芯光纤各个测点的波长漂移量并保存。

首先将蒙皮固定在曲率块上，并连接扇入扇出装置。通过解调仪和LabView软件，采集七芯光纤的中间纤芯和三根旁轴纤芯的波长数据，两根光纤共16个测点，4个纤芯的数组为一组，保存为excel表格。测量完成后，换不同曲率块进行相同的步骤，共得到三种曲率下的波长数据。将数据代入算法中得到蒙皮的空间坐标，根据坐标绘制重构图像。

3.2 实验测试及结果分析

蒙皮表面布设的两根多芯光纤传感器上16个测点的波长漂移量见表2～表4，曲率块曲率K分别为10 m-1、12.5 m-1、15.38 m-1。图8所示为不同曲率下的蒙皮三维重构图像，可以看出，随着标准曲率块曲率的增大，三维重构图像曲率也增大。在不同曲率的变形情况下，三维重构图像与标准曲率块曲率基本吻合，在部分重构点有较大偏差。

为了验证重构方法的有效性和精度，根据实验的测量结果，以标准的曲率块曲率为基准，使用曲率重构误差计算公式计算各测点的曲率重构误差e：

e=|K－k|/K（21）

式中，K为标准曲率块曲率；k为重构曲率。

将三种不同曲率下的测点重构数据与标准曲率进行对比，得到表5，即K分别为10 m-1、12.5 m-1和15.38 m-1时，计算得到的曲率和标准曲率之间的误差值，同时得到了平均曲率和平均误差。表5中，“平均”表示不同曲率的重构平均误差。可以看出，各个测点的重构曲率在标准曲率附近波动，随着曲率的增大，平均重构误差并没有明显增大，证明本系统和重构方法的有效性。在局部重构点误差稍大于平均值，主要原因是在传感器封装过程中产生了较大误差，导致不同曲率情况下在相同测点附近误差明显大于其他测点误差。

经计算，三种不同曲率下的蒙皮变形重构平均误差最小为2.09%，最大为5.6%，平均重构误差为3.5%，曲率重构精度比较高。实验数据表明，本文方法对不同曲率下的蒙皮变形重构具有较高的精度，能够满足变构型飞行器的变形监测需求。

4 结论及展望

本文针对变构型飞行器蒙皮变形检测的需求，提出一种基于光纤传感的变构型飞行器柔性蒙皮形状光纤重构方法，实现飞行器飞行过程中的变形监测。基于光纤光栅应变传感原理，推导了光纤应变和曲率之间的关系，建立了光纤传感局部坐标系和全局坐标系之间的转换矩阵。研究了一种空间曲线拟合方法和基于曲线拟合的三维变形重构算法。同时，为减小光纤传感器的测量误差，对传感器的应变灵敏度进行了标定。最后，为了验证本文方法的有效性，对柔性蒙皮样件在不同曲率下的三维变形重构进行了实验测试。实验结果表明，该方法对不同曲率的变形有较高的重构精度，柔性蒙皮样件在0～15.38 m-1曲率的变形范围内，形状重构方法的平均误差为3.5%，最小误差不足2.1%，在航空航天器蒙皮卫星监测上有较高的使用价值，具有良好的发展和应用前景。未来计划在飞行器机身、机翼等更复杂的结构上验证该重构方法的有效性，并进行风洞测试。

参考文献：

［1］ 王欣. 热冲击作用下含缺陷超高温陶瓷结构的损伤行为数值模拟［D］. 哈尔滨：哈尔滨工程大学， 2011.

WANG Xin， Numerical Simulation on Damage Evolution of Ultra High Temperature Ceramics with Micro Crack under The rmal Shock Condition［D］. Harbin：Harbin Engineering University， 2011.

［2］ 馬婧雪. 含安全边界的TBCC组合发动机控制研究［D］. 哈尔滨：哈尔滨工业大学， 2018.

MA Jingxue. Control Study for Over-under TBCC Engine with Safety Boundaries［D］. Harbin：Harbin Institute of Technology， 2018.

［3］ NICOLAS M J， SULLIVAN R W， RICHARDS W L. Large Scale Applications Using FBG Sensors：Determination of In-flight Loads and Shape of a Composite Aircraft Wing［J］．Aerospace， 2016， 3（3）：18-32.

［4］ BANG H， SHIN H， JU Y. Structural Health Monitoring of a Composite Wind Turbine Blade Using Fiber Bragg Grating Sensors［C］∥Proceedings， Sensors and Smart Structures Technologies for Civil， Mechanical， and Aerospace Systems. San Diego， 2010：76474H.

［5］ 张钰珏. 基于光纤光栅传感网络的变形监测研究［D］. 南京：南京航空航天大学， 2016.

ZHANG Yujue. Research on the Deformation Monitoring Based on Fiber Bragg Grating［D］. Nanjing：Nanjing University of Aeronautics and Astronautics， 2016.

［6］ 曲道明， 孙广开， 李红， 等. 变形机翼柔性蒙皮形状光纤传感及重构方法［J］. 仪器仪表学报， 2018， 39（1）：144-151.

QU Daoming， SUN Guangkai， LI Hong， et al. Optical Fiber Sensing and Reconstruction Method for Morphing Wing Flexible Skin Shape［J］. Chinese Journal of Scientific Instrument， 2018， 39（1）：144-151.

［7］ WADA D， HIROTAKA I， MASATO T， et al. Flight Demonstration of Aircraft Wing Monitoring Using Optical Fiber Distributed Sensing System［J］. Smart Materials and Structures， 2019， 28：055007.

［8］ DVORAK M， RUZICKA M， KABRT M. Design of Embedded FBG Sensor System for Ultralight Aircraft Wing Monitoring［C］∥7th International Conference on Structural Health Monitoring of Intelligent Infrastructure. Turin， 2015：208.

［9］ KRESSEL I， BALTER J， SOVRAN I， et al. HighSpeed， Inflight Structural Health Monitoring System for Medium Altitude Long Endurance Unmanned Air Vehicle［C］∥7th European Workshop on Structural Health Monitoring. Nantes， 2014：273-280.

［10］ NICOLAS M J， SULLIVAN R W， RICHARDS W L. Large Scale Applications Using FBG Sensors：Determination of In-flight Loads and Shape of a Composite Aircraft Wing［J］. Aerospace， 2016， 3（3）：18-18.

［11］ CIMINELLO M， FENZA A D， DIMINO I， et al. Skin-spar Failure Detection of a Composite Winglet Using FBG Sensors［J］. Archive of Mechanical Engineering， 2017， 64（3）：287-300.

［12］ WADA D， HIROTAKA I， MASATO T， et al. Flight Demonstration of Aircraft Fuselage and Bulkhead Monitoring Using Optical Fiber Distributed Sensing System［J］. Smart Materials and Structures， 2018， 27：025014.

［13］ WADA D， HIROTAKA I， MASATO T， et al. Flight Demonstration of Aircraft Wing Monitoring Using Optical Fiber Distributed Sensing System［J］. Smart Materials and Structures， 2019， 28：055007.

［14］ 王寅， 朱振宇， 陈志平， 等. 一种适于柔性无人机机翼形变的测试方法［J］. 计算机测量与控制， 2012， 20（11）：2894-2896.

WANG Yin， ZHU Zhenyu， CHEN Zhiping， et al. A Method of Wing Shape Predictions for Highly Flexible UAVS［J］. Computer Measurement and Control， 2012， 20（11）：2894-2896.

［15］ 袁慎芳， 闫美佳， 张巾巾， 等. 一种适用于梁式机翼的变形重构方法［J］. 南京航空航天大学学报， 2014， 46（6）：825-830.

YUAN Shenfang， YAN Meijia， ZHANG Jinjin， et al. Shape Reconstruction Method of Spar Wing Structure［J］. Journal of Nanjing University of Aeronautics and Astronautics， 2014， 46（6）：825-830.

［16］ 張科， 袁慎芳， 任元强， 等. 基于逆向有限元法的变形机翼鱼骨的变形重构［J］. 航空学报， 2020， 41（8）：244-254.

ZHANG Ke， YUAN Shenfang， REN Yuanqiang， et al. Shape Reconstruction of Self-adaptive Morphing Wings Fishbone Based on Inverse Finite Element Method［J］. Acta Aeronautica et Astronautica Sinica， 2020， 41（8）：244-254.

［17］ WANG W R， LU Y， ZHAO D Z， et al. Research on Large Deflection Deformation Reconstruction of Elastic Thin Plate Based on Strain Monitoring［J］. Measurement， 2020， 149：107000.

［18］ 祝航威， 何彦霖， 孙广开， 等. 螺旋型光纤传感软体操作臂状态测量及特性分析［J］. 红外与激光工程， 2020， 49（11）：221-229.

ZHU Hangwei， HE Yanlin， SUN Guangkai， et al. State Measurement and Sensing Characteristics Analysis of Soft Maniputator Basedon Helical Optical Fiber［J］. Infrared and Laser Engineering， 2020， 49（11）：221-229.

［19］ 闫洁， 李伟， 姜明顺， 等. 基于光纤光栅传感器的板状结构形态感知与三维重构技术［J］. 中国激光， 2020， 47（11）：231-240.

YAN Jie， LI Wei， JIANG Mingshun， et al. Shape Perception and Three-dimensional Reconstruction Technology of Plate Structure Based on Fiber Bragg Grating Sensor［J］. Chinese Journal of Lasers， 2020， 47（11）：231-240.

［20］ 何超江， 何彦霖， 骆飞， 等. 引入应变灵敏度矩阵的探针形状光纤测量方法［J］. 紅外与激光工程， 2021， 50（12）：410-418.

HE Chaojiang， HE Yanlin， LUO Fei， et al. Needle Shape Optical Fiber Measurement Method Introducing Strain Sensitivity Matrix［J］. Infrared and Laser Engineering， 2021， 50（12）：410-418.

［21］ 梁敏富， 方新秋， 陈宁宁， 等. 表贴式光纤光栅锚杆应变感知机理与应用研究［J］. 中国矿业大学学报2018， 47（6）：1243-1251.

LIANG Minfu， FANG Xinqiu， CHEN Ningning， et al. Strain Sensing Mechanism of Surface Bonded Fiber Bragg Grating Bolt and Its Application［J］. Journal of China University of Mining & Technology， 2018， 47（6）：1243-1251.

［22］ 张俊康， 孙广开， 李红， 等. 变形机翼薄膜蒙皮形状监测光纤传感方法研究［J］. 仪器仪表学， 2018， 39（2）：66-72.

ZHANG Junkang， SUN Guangkai， LI Hong， et al. Optical Fiber Shape Sensing of Polyimide Skin for Flexible Morphing Wing［J］. Chinese Journal of Scientific Instrument， 2018， 39（2）：66-72.