高二数学选择性必修一总复习(A 卷)答案与提示
一、单选题
1.D
2.D
3.C 提示:当a=1 时,直线l1:x+2y-8=0与直线l2:x+2y+4=0 平行,所以充分性成立。
因为直线l1:ax+2y-8=0与直线l2:x+ (a+ 1)y+ 4 = 0 平 行,所 以解得a=1,必要性成立。
所以“a=1”是“直线l1:ax+2y-8=0与直线l2:x+(a+1)y+4=0平行” 的充分必要条件。
4.A 提示:取过椭圆长轴与圆柱的轴所在的截面,如图1 所示。设圆柱的底面半径为r,可知截面为直角梯形ABCD。
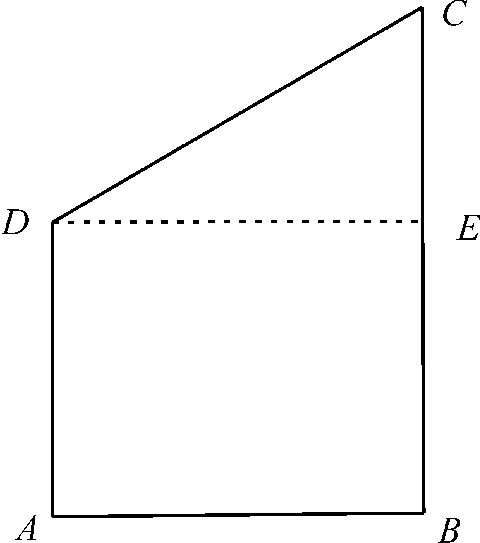
图1
过点D作DE⊥BC,垂足为点E,由题意可知,椭圆的短轴长为2b=2r,则b=r。
“切面”所在平面与底面所成的角等于∠CDE=30°,所以,
因此,该椭圆的离心率
5.C 提示:如图2,取C1在下底面的投影C,作CD⊥AB,垂足为D。
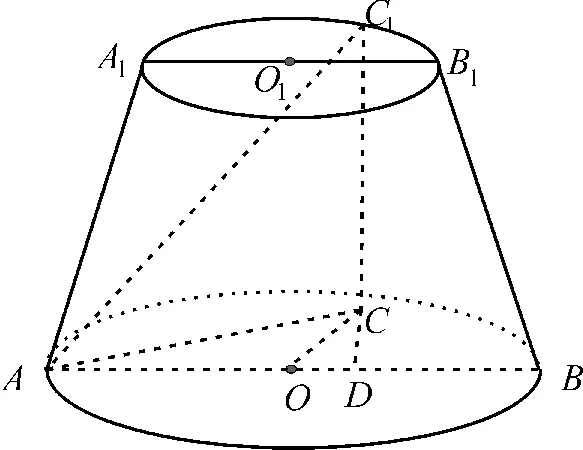
图2
连接CA,CO,CC1,则在上的投影向量是。


7.C 提示:设椭圆长轴为2a1,双曲线实轴为2a2,由题意可知|F1F2|=|F2P|=2c。
又因|F1P|+|F2P|=2a1,|F1P|-|F2P|=2a2,故|F1P|+2c=2a1,|F1P|-2c=2a2。
两式相减,可得a1-a2=2c。

整理得(x-4)2+y2=12,记为圆M。
因圆A:(x+2)2+y2=16 与圆M相交,故满足|PA|=|AB|=4的点P有2个。
因圆B:(x-2)2+y2=16 与圆M相交,故满足|PB|=|AB|=4的点P有2个。
因此,使△PAB为等腰三角形的点P共有4个。
二、多选题
9.BC 提示:对于A,a⊥b,b⊥c,不能得出a⊥c,也可能是a、c相交不一定垂直,选项A 错误。
对于B,假设向量a+b,b+c,c+a共面,则a+b=x(b+c)+y(c+a),x、y∈R。
化简得(x+y)c=(1-x)b+(1-y)a,所以a、b、c共面,这与已知矛盾,所以选项B正确。
对于C,根据空间向量基本定理知,对空间任一向量p,总存在有序实数组(x,y,z),使得p=xa+yb+zc,选项C正确。
对于D,因为{a,b,c} 是空间一个基底,所以a与b、c不共面,选项D 错误。



三、填空题
13.2或6


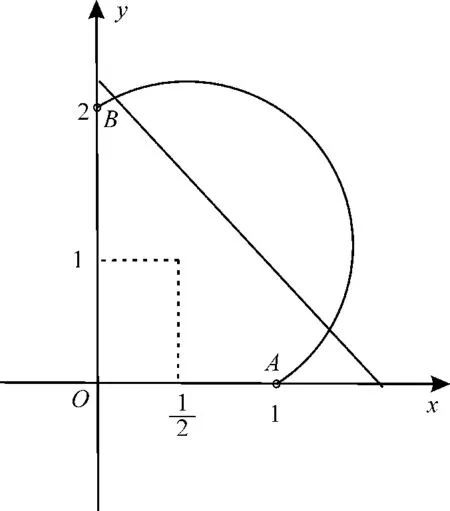
图4
当y=0时,x=1,则A(1,0);
当x=0时,y=2,则B(0,2)。
当直线t=x+y过A(1,0)时,t=1;
当直线t=x+y过B(0,2)时,t=2。
所以t>1。

四、解答题

因为菱形ABCD对角线互相垂直且互相平分,所以顶点B、D所在直线方程的斜率为
又因为(0,5)在直线BD上,所以顶点B、D所在直线方程为y-5=x,即x-y+5=0。
(2)直线AC,即x+y-5=0。由(1)知,顶点B、D所在直线方程为x-y+5=0,所以可设B(m,m+5)。
则点B到直线AC的距离为,解得m=±6。
因为点B的横坐标小于零,所以m=-6,即B(-6,-1)。
同理可求得D(6,11)。
18.(1)设经过A,B,D三点的圆的标准方程是(x-a)2+(y-b)2=r2。
将A,B,D三点坐标分别代入(x-a)2+(y-b)2=r2,得
将C(3,5)代入上面方程,式子也成立。
所以A,B,C,D四点共圆。
过A,B,C,D四点的圆的方程为(x-2)2+(y-3)2=5。
(2)根据光的反射原理,作与点M(-3,2)关于x轴对称的点M1(-3,-2),从M点发出的光线经x轴反射后,反射光线所在直线就是由M1向圆O1所作的两条切线所在的直线。
由题可知☉O1:(x-2)2+(y-3)2=5。
则切线的斜率一定存在,设切线方程为y+2=k(x+3),即kx-y+3k-2=0。
所以反射光线所在直线的方程为y+2)或y+2=2(x+3),即x-2y-1=0或2x-y+4=0。

选②。
因为抛物线C:y2=2px(p>0)的准线方程是,所以p=2,抛物线C的方程为y2=4x。
选③。
因为抛物线C:y2=2px(p>0)的通径是2p,所以2p=4,即p=2,抛物线C的方程为y2=4x。
(2)设A(x1,y1),B(x2,y2)。
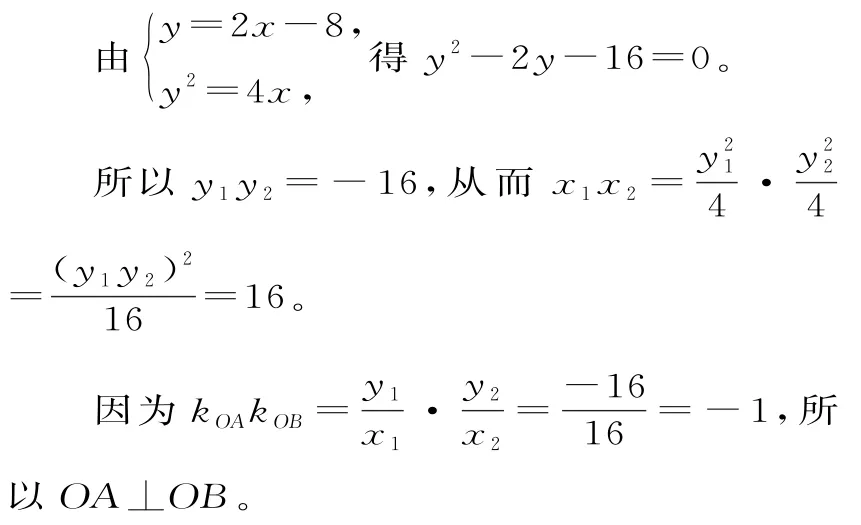
21.(1)已知AB//CD,CD⊂平面PCD,且AB⊄平面PCD,所以AB//平面PCD。
又AB⊂平 面PAB,平 面PAB∩平 面PCD=l,所以AB//l。
(2)已知△ABC是正三角形,E是BC中点,所以AE⊥BC。而BC//AD,所以AE⊥AD。又PA⊥平面ABCD,故以点A为坐标原点,AE,AD,AP所在直线分别为x,y,z轴,建立如图5所示的空间直角坐标系。


图5
设平面PCD的一个法向量是n=(x,y,z),则:



