高二数学选择性必修一总复习（B卷）答案与提示

一、单选题

1.B 2.B 3.B 4.D 5.D

6.B 提示:如图1,作直线2x+y=0,当直线上移与圆x2+(y-1)2=1 相 切 时,z=2x+y取最大值。此时,圆心(0,1)到直线2x+y-z=0的距离等于1,即

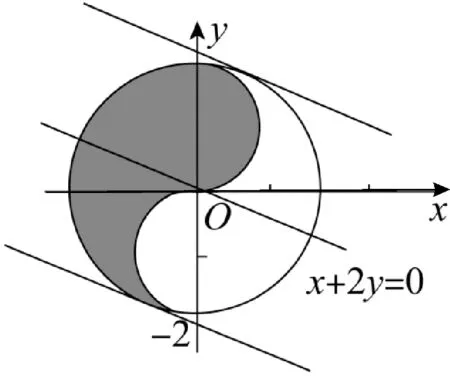
图1

解得z的最大值为

当下移与圆x2+y2=4 相切时,2x+y取最小值。

所以z=2x+y的最大值与最小值之和是1-。

7.C 提示:直线l:kx-y-2k+1=0,即为k(x-2)+1-y=0,可得直线恒过定点(2,1)。

圆C2:(x-2)2+(y-1)2=1的圆心为(2,1),半径为1,且C,D为直径的端点。

8.C 提示:如图2所示,建立直角坐标系。

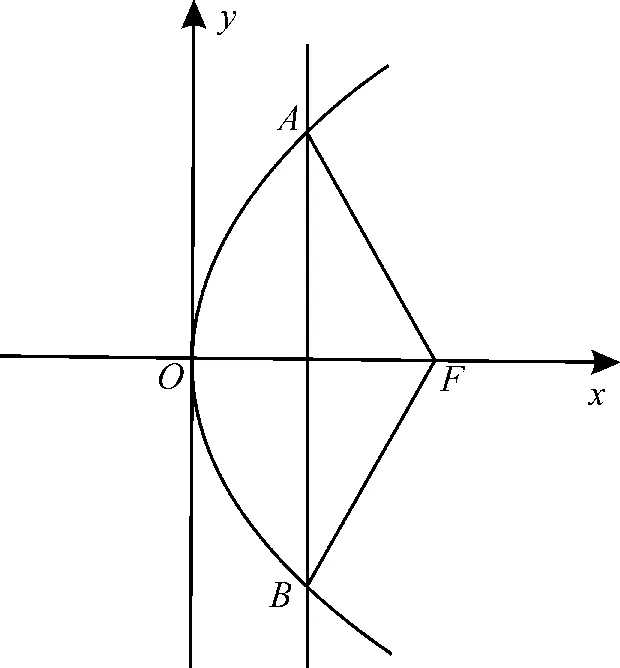
图2

设抛物线的标准方程为y2=2px(p>0),

二、多选题

9.AC 提示:设椭圆的右焦点F′,连接PF′,QF′,根据椭圆对称性可知四边形PFQF′为平行四边形。

则|QF|=|PF′|,且由∠PFQ=120°,可得∠FPF′=60°。

所以|PF|+|PF′|=4|PF′|=2a,则

设M(x0,y0),P(x1,y1),则Q(-x1,-y1)

10.AB 提示:在正方体ABCD-A1B1C1D1中,以点D为原点,建立如图3所示的空间直角坐标系,令|AB|=2。

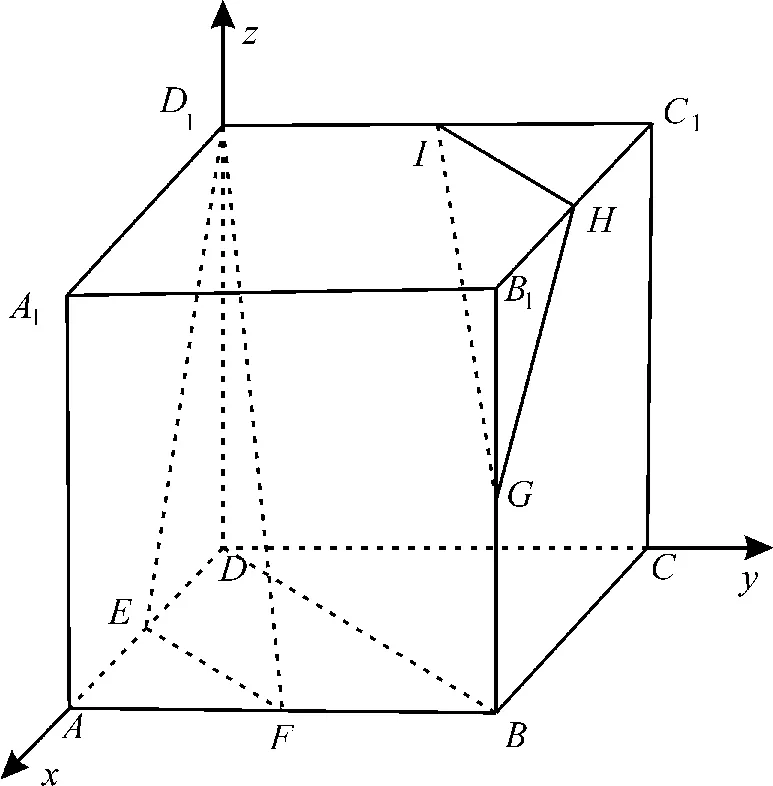
图3

则D(0,0,0),D1(0,0,2),B(2,2,0),E(1,0,0),F(2,1,0),G(2,2,1),H(1,2,2),I(0,1,2)。

由双曲线的性质可知,若过平面内的任意一点的直线与双曲线的渐近线平行,只与双曲线有一个交点,所以不存在一点,使过该点的任意直线与双曲线C有两个交点,故C错误。

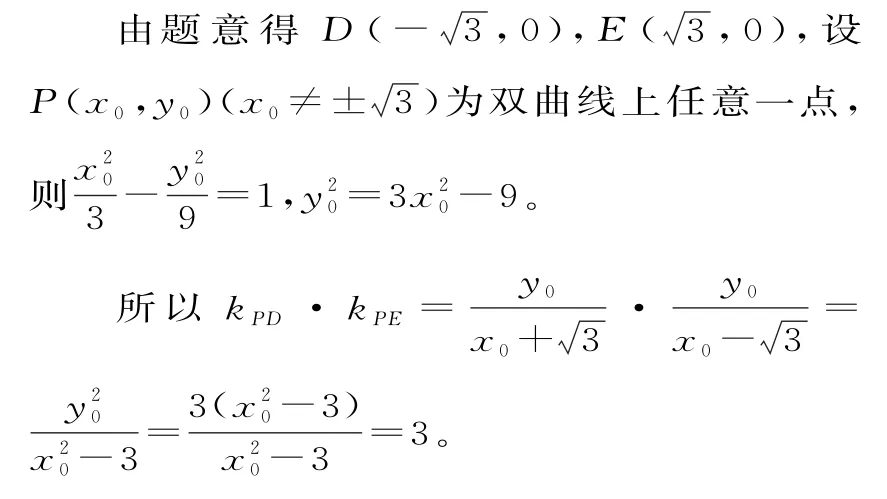
因此,双曲线C上存在无数个点,使它与D,E两点的连线的斜率之积为3,D正确。

故选ABD。

12.ACD 提示:如图4,取AD的中点N,连接MN。

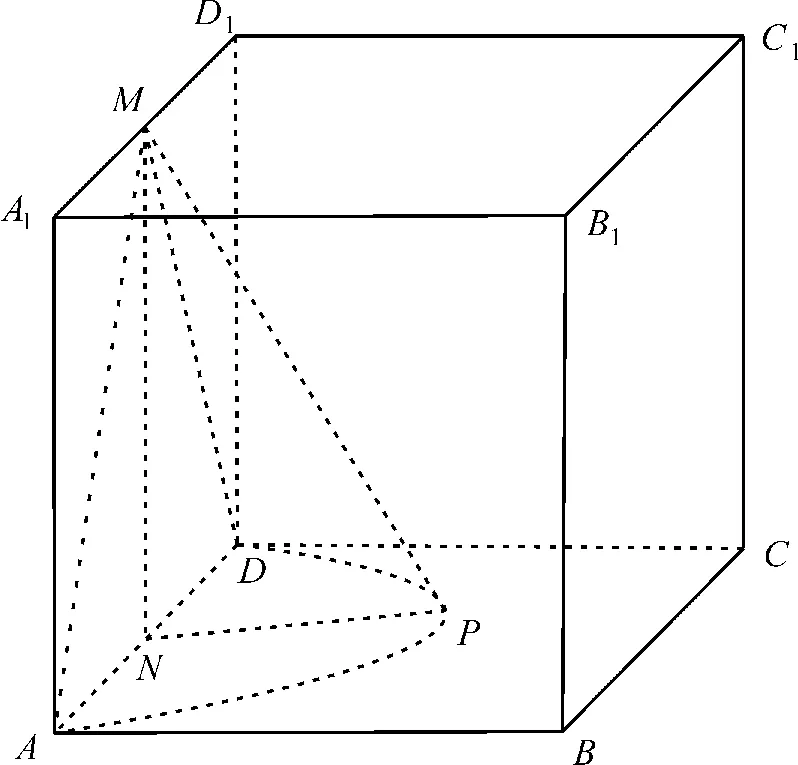
图4

因为A1D1//AD且|A1D1|=|AD|,且M、N分别为A1D1、AD的中点,所以A1M//AN且|A1M|=|AN|,四边形AA1MN为平行四边形。

可得MN//AA1,且|MN|=|AA1|=4。

因AA1⊥底面ABCD,故MN⊥底面ABCD。因为NP⊂底面ABCD,所以MN⊥NP。

故点P的轨迹长度为π×2=2π,A正确。

以A为 原 点,AB、AD、AA1所 在 直线分别为x、y、z轴,建立空间直角坐标系,如图5。

图5

则A1(0,0,4),C(4,4,0),M(0,2,4),B(4,0,0),D(0,4,0),B1(4,0,4)。

如图4,挖去部分为半圆锥,原正方体的表面积S=6×4×4=96。

挖去部分的面积S1=8+2π,新增部分的面积

所剩部分几何体的表面积S-S1+S2=,故D 正确。

三、填空题

13.x+y-3=0

14.4 提示:由题意,显然过点M(-1,m)作抛物线C:y2=2px的切线的斜率存在,可设斜率为k,则该切线方程为y-m=k(x+1),即y=kx+k+m。

由于切线与抛物线只有唯一交点,则Δ=(2k2+2km-2p)2-4k2(k2+2km+m2)=0,整理可得2k2+2km-p=0。

由题意可知kMA,kMB为方程2k2+2kmp=0的两个根,则

由题意,设直线AB的方程为

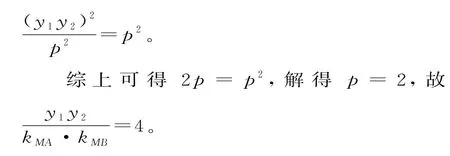
图6

16.①③④ 提示:设点P(x,y)。

对于①,若曲线C表示点(a,b),则,化简可得(x-a)2+(y-b)2≤4。

所以,点集D={P|d(P,C)≤2}所表示的图形是以点(a,b)为圆心,半径为2的圆及其内部。

点集D={P|d(P,C)≤2}所表示的图形的面积为π×22=4π,①正确。

对于②,若曲线C表示以点M(a,b)为圆心,半径为2的圆。

设Q为曲线C上一点,当点P在曲线C内时,当且仅当Q、P、M三点共线时,等号成立。

所以,d(P,C)=2-|MP|≤1,可得|MP|≥1,此时1≤|MP|<2。

当 点P在 曲 线C外 时,,当且仅当Q、P、M三点共线时,等号成立。

所以,d(P,C)=|MP|-2≤1,可得|MP|≤3,此时2<|MP|≤3。

当点P在曲线C上时,线段PQ的长不存在最小值。

综上所述,1≤|MP|<2或2<|MP|≤3,即1≤(x-a)2+(y-b)2<4或4<(xa)2+(y-b)2≤9。

所以,点集D={P|d(P,C)≤1}所表示的图形是夹在圆(x-a)2+(yb)2=1 和圆(x-a)2+(y-b)2=9 的 区 域(但 不包括圆(x-a)2+(y-b)2=4的圆周),如图7。

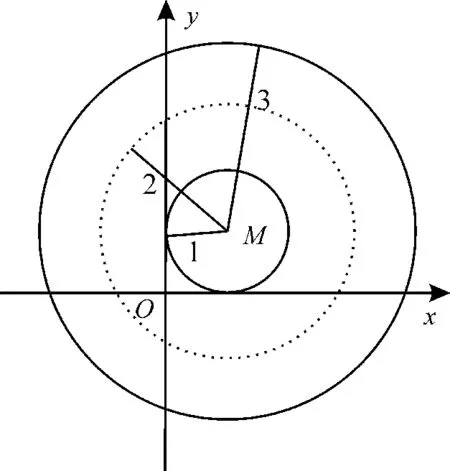
图7

此时,点集D={P|d(P,C)≤1}所表示图形的面积为π×(32-12)=8π,②错误。

对于③,不妨设曲线C为线段AB,且|AB|=2。

当点Q与点A重合时,由①可知,点集D表示的是以点A为圆心,半径为1的圆。

当点Q与点B重合时,点集D表示的是以点B为圆心,半径为1的圆。

故当点Q在线段AB上滑动时,点集D表示的区域是一个边长为2 的正方形EFGD和两个半径为1的半圆所围成的区域,如图8。

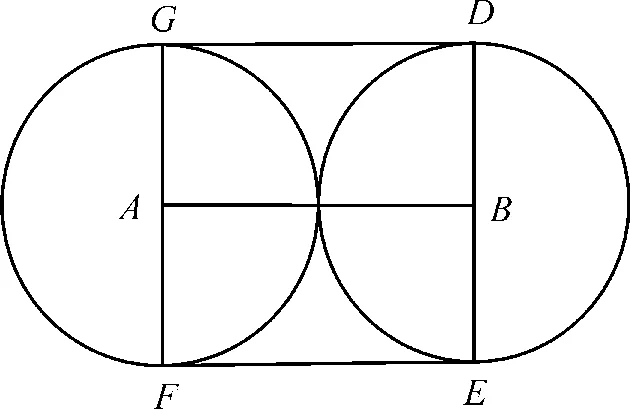
图8

此时,点集D的面积为π×12+22=π+4,③正确。

对于④,若曲线C是边长为9的等边三角形,设等边三角形为△ABC。

由③可知,点集D构成的区域由矩形ABRD、ACFE、BCWL,以及分别由点A、B、C为圆心,半径为1,圆心角为的三段圆弧,和夹在等边△ABC和等边△STU中间的部分(包括边界),如图9。

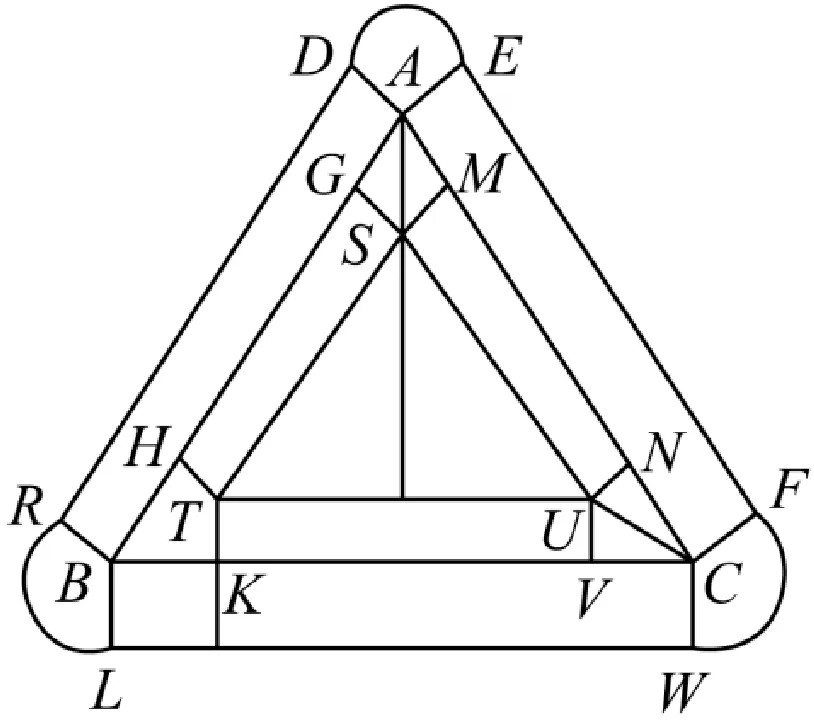
图9

四、解答题

18.(1) 由题意可知,C上任意一点M(x,y)到定点F(2,0)的距离与它到直线x=-2的距离相等,轨迹为抛物线。

设方程为y2=2px,则,p=4,故抛物线C的方程为y2=8x。

(2)设直线AB的方程为x=ty+2,

则lOA

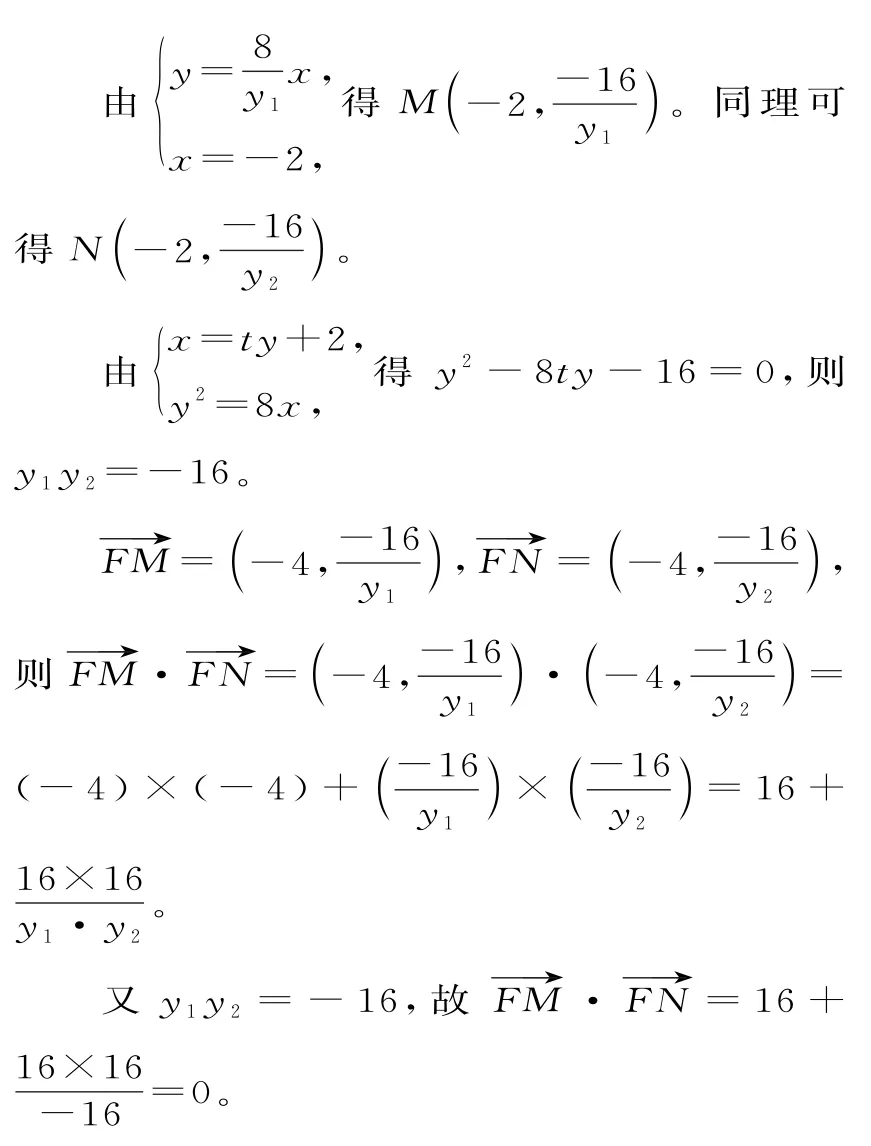
因此,以线段MN为直径的圆经过点F。

19.(1)设点E到AB的距离为h。因为△ABE的面积为4,|AE|=2,|AB|=4,所以,即h=2。

因为|AE|=2,所以AE⊥AB,即AA′⊥AB。

又AD⊥AA′,AD∩AB=A,AD⊂平面ABCD,AB⊂平面ABCD,所以AA′⊥平面ABCD。

当λ=1时,,即P为FH的中点,则P在B′D′上。

又因为DD′//AA′,所以DD′⊥平面ABCD。

因为AC⊂平面ABCD,所以DD′⊥AC。

又AC⊥BD,DD′∩BD=D,DD′⊂平面BDD′B′,BD⊂平面BDD′B′,所以AC⊥平面BDD′B′。

又BP⊂平面BDD′B′,所以BP⊥AC。

(2)因为AA′⊥平面ABCD,BD⊂平面ABCD,所以AA′⊥BD,即AE⊥BD。

又AC⊥BD,AE∩AC=A,AE⊂平面ACC′E,AC⊂平面ACC′E,所以BD⊥平面ACC′E。

因此,多面体B-ACC′E的体积

(3)由(1)知,DA,DC,DD′两两垂直。

如图10,以D为原点,DA,DC,DD′所在直线分别为x,y,z轴,建立空间直角坐标系。

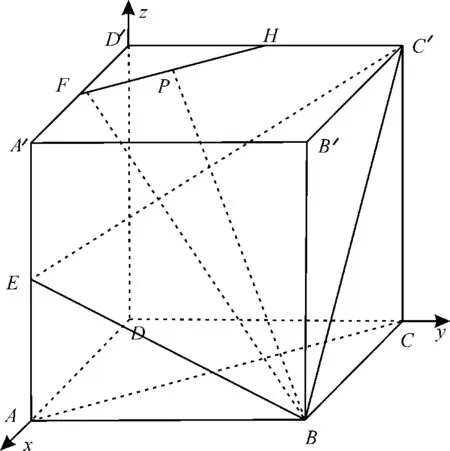
图10

则D(0,0,0),B(4,4,0),E(4,0,2),C′(0,4,4),F(2,0,4),H(0,2,4)。

所以当λ=2 时,直线BP与平面BC′E夹角的正弦值为

20.(1)由题意得,圆C:(x-1)2+y2=16,则圆心C(1,0),半径r=4。

设PN中点为K,则QK为线段PN的垂直平分线,|PQ|=|QN|。

而|QN|+|QC|=|QP|+|QC|=r=4>|NC|=2,所以Q点轨迹是以C,N为焦点,长轴长为4 的椭圆,即a=2,c=1,则b2=a2-c2=3。

所以点Q的轨迹方程为

(2)设A(x1,y1),B(x2,y2),由题意可得x1,x2∈(0,2)。

又直线PA的斜率为2,故直线PB的斜率为

(2)①当切线PA,PB的斜率都存在时,设A(x1,y1),B(x2,y2),切线PA,PB方程为y-yi=ki(x-xi),i=1,2。

由(1)得(4-x2i)k2+2xiyiki+1-y2i=0,i=1,2。(*)

②当切线PA,PB的斜率有一个不存在时,不妨设PB斜率不存在,且B(2,0),P(2,1),A(0,1)。

而k≠0,|m|≠1,因此(|F1M|+|F2N|)·|MN|<4。

ii)当k=0时,四边形F1MF2N为矩形。

此时(|F1M|+|F2N|)·|MN|=(1+1)×2=4。

由i),ii)可知,(|F1M|+|F2N|)·|MN|的最大值为4。