2023 年高考之椭圆考点解读
■河南省许昌市高中数学胡银伟名师工作室 胡银伟
从近年高考命题情况来看,对椭圆定义、标准方程、几何性质的考查常以选择题、填空题的形式出现,而直线与椭圆的位置关系主要出现在解答题中。同学们应能够熟练从“数”与“形”两个角度来探究椭圆的取值范围、对称性、顶点、离心率等几何性质,且熟练利用代数法解答直线与椭圆有关的最值、定点、定值等问题。下面我们结合2023年高考真题,对椭圆的考点进行解读。
动力特性分析模型中,桥面板采用板单元模拟,其余杆件采用梁单元模拟,铺装和护栏等作为荷载模拟,全桥共划分节点数量361个,梁单元数量626个,板单元数量264个。
考点1 对椭圆的方程及简单几何性质的考查
例1(1)【2023 年全国甲卷文数第7题】设F1,F2为椭圆的两个焦点,点P在椭圆C上,若,则|PF1|·|PF2|=( )。
2.2.1 评价单元划分 采用土壤图、土地利用现状图和行政区划图的空间叠加,共划分16 536个评价单元。
A.1 B.2 C.4 D.5
设F1到AB的 距 离 为d1,F2到AB的距离为d2,易知,则
2.2.3 专家意见的协调程度 在变异系数方面,第1轮3级指标共59个,变异系数<0.5的3级指标有52个,占88%。第2轮的3级指标变异系数均<0.5。
古希腊缔造出了众多优秀的哲学家,苏格拉底就是当时非常突出的一位。他开创了“伦理哲学”,标志着哲学上的一种转变,从此,人们不但研究自然,而且更多地将重心放在研究人类自身上。另一个重要的哲学家就是柏拉图,他在哲学方面的地位和影响力在雅典乃至世界上都相当巨大。柏拉图是苏格拉底的学生,是亚里土多德的老师,亚里土多德与柏拉图是西方哲学界最有影响力的两个人,柏拉图主张形而上学的观念,而亚里土多德更注重从感官获得认知和知识。
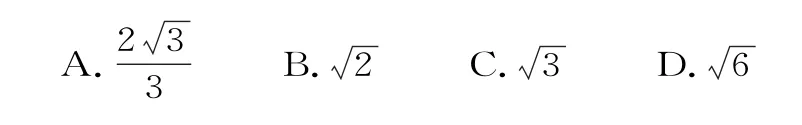
(3)【2023年全国甲卷理数第12题】设O为坐标原点,F1,F2为椭圆C的两个焦点,点P在椭圆C上,cos∠F1PF2=,则|OP|=( )。
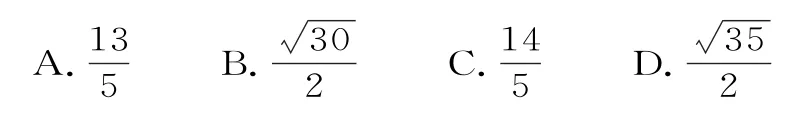
命题意图:本例的3 个题目都是考查椭圆的方程及简单的几何性质,考查同学们逻辑推理、直观想象及数学运算等核心素养。
解题思路:(1)方法一,根据焦点三角形面积公式求出△PF1F2的面积,即可求解;方法二,可根据椭圆的定义及勾股定理进行解答。(2)由给定的椭圆方程,结合离心率的定义进行解答。(3)方法一,根据焦点三角形的面积公式求出△PF1F2的面积,可得点P的坐标,从而得|OP|的值;方法二,先利用椭圆的定义及余弦定理求出|PF1|·|PF2|,|PF1|2+|PF2|2的值,再结合中线的向量公式及数量积可得解;方法三,先利用椭圆的定义及余弦定理求出|PF1|2+|PF2|2的值,再根据中线定理求解。


考点解读:在本例(1)、(3)的解答过程中,有效地利用了椭圆中焦点三角形的面积公式的二级结论,使得问题易解。
例3【2023 年全国乙卷文数第21题】已知椭圆C的离心率是,点A(-2,0)在椭圆C上。
命题意图:本例考查直线与椭圆的位置关系、点到直线的距离及与椭圆有关的三角形的面积,同时考查同学们直观想象、逻辑推理及数学运算等核心素养。
随着社会发展进步,以及环境污染等各种因素影响下,肺部真菌感染发生率呈持续性上升发展趋势,对患者的正常生活、生活质量以及身心健康均造成较严重影响。肺部真菌感染患者主要症状包括疼痛、原发症状发热以及不同程度的呼吸困难等,且无特异性,因此早期诊断、早期治疗该疾病的难度较大。采取何种检查方法可以更有利于早期诊断、早期有效鉴别肺部真菌感染,以提高临床治疗效果十分重要。本次研究工作旨在探讨CT在诊断与鉴别肺部真菌感染中的可行性研究。现报道如下。
(2)涉及焦点三角形面积,可把|PF1|,|PF2|看作一个整体,运用|PF1|2+|PF2|2=(|PF1|+|PF2|)2-2|PF1|·|PF2|及余弦定理求出|PF1|·|PF2|,无须单独求解。
与椭圆有关的二级结论比较多,由本例(1)、(3)的解答过程可以看出,恰当地掌握、应用常用的二级结论可为我们的解题打开便利之门。
考点2 对直线与椭圆位置关系的考查
因为直线与椭圆相交于A,B点,所以Δ=36m2-4×4(3m2-3)=48-12m2>0,解得-2 (1)椭圆的定义具有双向作用,若|MF1|+|MF2|=2a(2a>|F1F2|),则点M的轨迹是椭圆;反之,椭圆上任意一点M到两焦点的距离之和必为2a。 解题思路:首先联立直线方程与椭圆方程,利用Δ>0,求出m的取值范围,再根据三角形面积比得到关于m的方程,从而得解。 例2【2023 年全国新课标Ⅱ卷第5题】已知椭圆C:的左、右焦点分别为F1、F2,直线y=x+m与椭圆C交于A,B两点,若△F1AB面积是△F2AB面积的2倍,则m=( )。 如果我们还生活在一百年前的上海滩、一百五十年前的美国西部,或者两百年前的雾都伦敦,对于大部分人来说,是必须教孩子打回去的。一方面在一个混乱的年代,信奉的是力量至上的原则,整个社会的法则就是如此,因此必须从小让孩子了解并且适应这样的环境,才能在以后的生活中有更强的生存能力。“打回去”是这种崇尚暴力年代的必修课。 考点解读:解答直线与椭圆相交的问题,常用到“设而不求”的方法,即联立直线和椭圆的方程,消去y(或x)得到一元二次方程,然后借助根与系数的关系,并结合题设条件,建立有关参变量的等量关系求解。利用公式计算直线被椭圆截得的弦长是在方程有解的情况下进行的,不要忽略方程根的判别式。 椭圆定义在焦点三角形中的应用技巧如下。 (1)求椭圆C的方程; (2)过点(-2,3)的直线交椭圆C于P,Q两点,直线AP,AQ与y轴的交点分别为M,N,证明:线段MN的中点为定点。 命题意图:本例是考查与椭圆有关的定点问题,考查同学们逻辑推理、直观想象及数学运算等核心素养。 解题思路:(1)依题意列式求解a,b,c,进而得结果;(2)设直线PQ的方程,进而可求点M,N的坐标,结合韦达定理验证为定值即可。 CMV感染是艾滋病患者最常见的疱疹病毒感染,可分为CMV血症和器官受累的CMV病。CMV可侵犯患者多个器官系统,包括眼睛、肺、消化系统、中枢神经系统等,其中CMV视网膜脉络膜炎是艾滋病患者最常见的CMV感染。 (2)由题意知,直线PQ的斜率存在,设PQ:y=k(x+2)+3。 所以线段MN的中点是定点(0,3)。 截至2016年底,我国已并网发电的秸秆直燃发电项目近260个,累计并网装机容量约为6400MW。主要分布在山东省、安徽省、黑龙江省、江苏省、河北省、湖北省、吉林省、河南省、湖南省、山西省。 考点解读:近年高考命题对圆锥曲线中的定点、定值问题考查较多,是近年高考命题的热点,且常考常新,试题综合性较强,难度较大。圆锥曲线中定点问题的常用解法:(1)引进参数法,引进动点的坐标或动直线中系数为参数表示变化量,再研究变化的量与参数何时没有关系,找到定点;(2)特殊到一般法,根据动点或动直线的特殊情况探索出定点,再证明该定点与变量无关。圆锥曲线中定值问题的常用解法:(1)从特殊入手,求出定值,再证明这个值与变量无关;(2)直接推理、计算,并在计算推理的过程中消去变量,从而得到定值。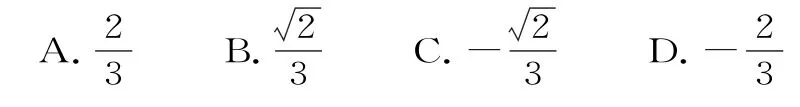

考点3 对椭圆的综合应用的考查


