聚焦圆锥曲线的离心率问题

■广东省汕头市澄海凤翔中学 徐春生

一、由定义求离心率

例1设F1、F2分别是椭圆)的左、右焦点,M为直线y=2b上的一点,△F1MF2是等边三角形,则椭圆C的离心率为( )。

解析:因为△F1MF2是等边三角形,M为直线y=2b上的一点,所以M(0,2b),|MF1|=|F1F2|,即

因为b2=a2-c2,所以4a2=7c2,即a=。

所以椭圆C的离心率,选C。

点评:根据椭圆或双曲线的定义,求出a,c或列出关于a,c的等式,得到关于e的方程,进行求解。

二、由几何性质求离心率

例3设F1、F2分别为双曲线C:的左、右焦点,P是双曲线C上一点。若|PF1|+|PF2|=6a,且△PF1F2的最小内角为30°,则双曲线C的离心率为_____。

解析:根据双曲线的对称性,不妨设点P在第一象限,则解得

又因为|F1F2|=2c,所以△PF1F2中|PF2|最小,故∠PF1F2=30°。

解析:如图1,设PF1的中点为M,连接PF2。因为O为F1F2的中点,所以OM//PF2, ∠PF2F1=∠MOF1=90°。

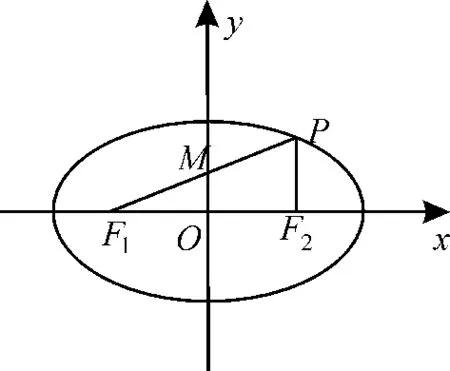
图1

因为∠PF1F2=30°,所 以|PF1| = 2|PF2|,|F1F2| =

由椭圆的定义得2a=|PF1|+|PF2|=3|PF2|,所以

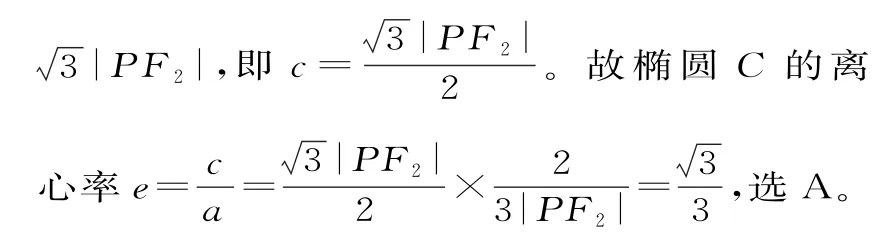
点评:涉及焦点三角形的题目往往利用圆锥曲线的定义及三角形中的正弦定理、余弦定理、三角形面积公式等来求得e的值。

三、由齐次方程求离心率

例5已知椭圆b>0),A,B分别为椭圆C的左顶点和上顶点,F为右焦点,且AB⊥BF,则椭圆C的离心率为_____。

解析:在△ABF中,|BF|=a,|AF|=a+c。

由AB⊥BF,得|AB|2+|BF|2=|AF|2。将b2=a2-c2代入,得a2-ac-c2=0,即e2+e-1=0,解得

因为0

例6双曲线若矩形ABCD的四个顶点在双曲线E上,AB,CD的中点为双曲线E的两个焦点,且2|AB|=3|BC|,则双曲线E的离心率是 。

图2

又因为2|AB| =3|BC|,所以2c,即2b2=3ac。

因为b2=c2-a2,所以2(c2-a2)=3ac。两边同除以a2并整理得2e2-3e-2=0,解得e=2或(舍去),所以双曲线E的离心率是2。

点评:利用定义以及图形中的几何关系建立关于参数a,b,c的关系式,结合c2=a2+b2(或a2=b2+c2),化简为参数a,c的关系式进行求解。