考虑测量误差的两阶段Wiener建模与可靠性分析

高新　叶楠　周坤　陶友瑞

摘要：针对现有的多阶段Wiener退化建模与可靠性分析中，大多忽略测量误差且未考虑退化过程中变点差异性的问题，建立了一种考虑测量误差的两阶段Wiener模型。将极大似然估计法和多维搜索算法相结合求出测量误差的估计值。考虑到变点的差异性，基于BIC最小准则估计出变点区间，同时根据变点位置确定漂移系数和扩散系数的估计值，再利用SSE最小准则求出变点的估计值，给出了基于变点分布区间的可靠性评估方法。最后，基于所建模型对RV减速器传动精度退化数据进行了实例分析。考虑测量误差及变点位置对退化建模的不确定性影响，进一步提高了产品的可靠性评估精度，能对产品的寿命做出更精准的预测。

关键词：多阶段退化；测量误差；Wiener过程；变点分布区间；寿命预测

中图分类号：TB114.3

DOI：10.3969/j.issn.1004-132X.2023.09.007

Two Stage Wiener Modeling and Reliability Analysis Considering Measurement Errors

GAO Xin1，2 YE Nan1，2 ZHOU Kun1，2 TAO Yourui1，2

Abstract： In the existing multi-stage Wiener degradation modeling and reliability analysis， most of them ignored the measurement errors and did not consider the differences of change points in the degradation processes. Considering measurement errors， a two-stage Wiener model was established and the maximum likelihood estimation method and multidimensional search algorithm were combined to obtain the estimated values of measurement errors. Considering the differences of change points， the change point interval was estimated based on BIC minimum criterion， at the same time， the estimated values of drift coefficient and diffusion coefficient were determined according to the positions of change points， and then the estimated values of change points were obtained by using SSE minimum criterion. A reliability evaluation method was given based on the distribution interval of change points. Finally， based on the established model， an example of RV reducer transmission accuracy degradation data was analyzed. Considering the uncertainty impacts of measurement errors and change point positions on degradation modeling， the reliability evaluation accuracy of the products is further improved and the life of the products may be predicted more accurately.

Key words： multi-stage degradation; measurement error; Wiener process; change point distribution interval; lifetime prediction

0 引言

隨着制造业水平的提高，在工业机器人、航空航天等领域出现了许多高可靠性、长寿命的产品，它们结构复杂、维修费用高，所以这类产品的可靠性评估和寿命预测是工程领域的重点和难点问题［1-2］。产品可靠性的提升使传统的寿命试验在有限的时间和成本下很难获得足够的失效数据，但很多产品的关键性能参数在使用过程中会缓慢发生退化，达到一定阈值后认定产品失效，这些性能退化数据提供了大量的可靠性分析信息，因此利用性能退化信息对产品进行可靠性评估成为了一种有效便捷的途径［3-5］。

在内部机理和外部环境作用下，产品的性能退化过程会呈现出随机不确定性，因此基于这种随机退化过程的可靠性建模方法备受欢迎［6-7］，其中，Wiener退化模型对这种随机退化过程具有良好的适应性，在各种领域得到了广泛的应用［8-10］。在产品的退化建模过程中测量误差会对退化模型的不确定性造成影响，目前已有很多学者在产品的建模中引入了测量误差。WHITMORE［11］最早将测量误差引入退化模型中，假设测量误差服从正态分布，并用数值分析方法验证了模型的可行性。PENG等［12］设测量误差和不同个体退化速率都服从高斯分布，提出了更一般化的带有测量误差的Wiener退化模型。文献［13-15］建立了线性和非线性的Wiener退化模型且考虑了随机效应和测量误差对退化模型的不确定性影响。但是，对于退化过程呈现多阶段的产品［16-19］，退化建模和可靠性分析中往往都忽略了测量误差的存在，且由于不同阶段的退化过程不同，每个阶段可能存在不同的测量误差。

在产品的多阶段退化过程中存在一个变点［20］，在该时刻产品的退化过程发生了改变，变点位置的确定是否合理也会对退化模型的不确定性造成影响。对于产品退化过程中的变点，大多数多阶段退化建模中忽略了变点位置的个体差异性［21-22］，鄢伟安等［19］基于LCD退化数据建立了两阶段的线性Wiener模型，但是假设变点位于同一位置，即产品在相同测试时刻发生阶段性变化，忽视了产品个体的差异性，且没有考虑测量误差对退化建模的不确定性，会影响退化建模的准确性。

考虑到测量误差及变点对退化建模的不确定性影响，本文建立了一种考虑测量误差的两阶段Wiener退化模型，利用极大似然估计法和多维搜索算法对模型参数进行估计，而且考虑到退化过程中变点的差异性，基于BIC和SSE最小准则对变点区间及变点值进行了合理估计，然后进一步根据3σ原则建立变点分布区间，给出了基于变点分布区间的可靠性评估和寿命预测的方法。最后，对RV减速器传动精度退化数据进行实例分析，与考虑变点的两阶段Wiener可靠性建模方法进行了比较。

1 考虑测量误差的两阶段Wiener过程建模

1.1 模型描述

一些产品在退化过程中呈现出两阶段甚至多阶段的退化现象，即在退化轨迹中的某一时刻（称为变点）产品退化过程由某一阶段进入另一阶段，在变点前后产品服从不同的退化过程。例如在某些半导体激光器的退化过程中，开始一段时间内退化速度很快，当退化到某一时刻（变点），退化速度明显变缓［20］。目前大多数建模只考虑单一阶段的退化过程而忽视了产品的内部失效机理和外部环境的变化，很多产品可能会呈现多阶段的退化规律，所以可以先利用数值工具对产品的性能退化数据进行轨迹拟合，观测是否具有明显的多阶段特征，然后考虑是否应该建立多阶段的退化模型。

2.2 寿命评估

对第一阶段、过渡阶段和更新后第二阶段的可靠度函数分别进行积分再求和可求得产品的平均寿命：

剩余寿命的α-分位点qα（t）是工程上的重要指标，它表示产品在某一时刻正常工作的前提下能够以概率1-α继续正常工作的时间，可以用来预测产品的剩余寿命。qα（t）与可靠度函数R（t）之间的关系为

R（t+qα（t））=（1－α）R（t）（28）

qα（t）=R－1（（1－a）R（t））－t（29）

当t=0，α=0.5时，q0.5（0）为产品的中位寿命；当t=0，α=0.1时，q0.1（0）为产品的0.1-分位点寿命。

3 实例分析

为了验证本文方法的合理性与有效性，按照上述模型参数估计及可靠性评估方法对文献［26］中RV减速器传动精度退化数据进行实例研究。3台RV减速器传动精度退化量随时间的变化情况见图2，可以看出，在1500～2000 h减速器传动精度退化量小幅下降，之后传动精度退化量又开始上升，传动精度退化数据呈现出两阶段的退化特征。设定RV减速器传动精度退化量的失效阈值D=20″。

针对每台样本，首先假设变点所在区间为［t1，t2），…，［tki，tki+1），…，［tmi-1，tmi），然后应用BIC准则计算相应的BIC值。不失一般性，以样本1为例进行说明，表1列出了样本1相应的BIC值，可以看出BIC（6）=42.17最小，所以样本1中存在变点，且变点区间为［1738.9，2035.8）。

表2给出了每台样本变点函数的系数，由变点函数的系数可知，变点δ在区间［tki，tki+1）上的SSEi值是递增的，所以在t=tki处SSEi值取最小值。

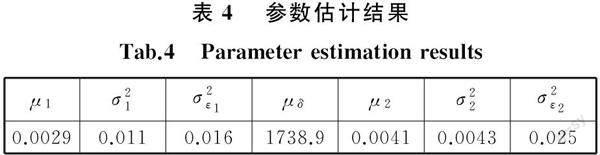
表3给出了每台样本变点所在区间及其估计值，由表3可得变点分布参数的估计值μ^δ=1738.9，σ^2δ=34.6。

本文方法全部参数估计结果见表4，可以看出第一、第二阶段的漂移系数μ和扩散系数σ差异比较大，这会引起第一、第二阶段的退化速率有

所不同，也会引起第一、第二阶段的测量误差有所差别，所以分段能更好地拟合性能退化数据曲线。

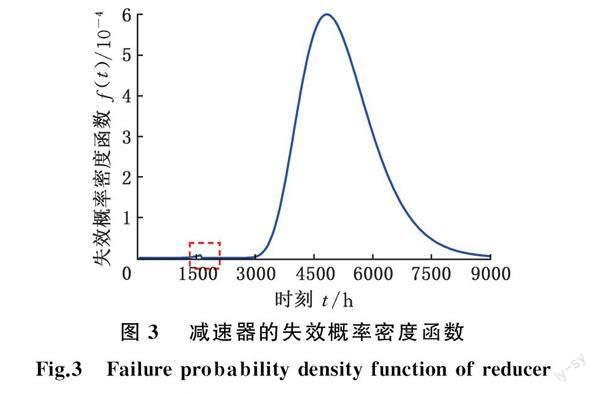
将本文参数的全部估计结果代入式（20）～式（26）可以得到减速器的失效概率密度函数图和可靠度函数图，见图3和图4。可以看出，在3500 h以后减速器的失效概率密度函数值显著增大，可靠度函数值的下降速率也开始加快，可以初步判断此时减速器开始进入了磨损加剧阶段。从图3红色框线处可以看出，在退化第一、第二阶段的变点处，失效概率密度函数曲线呈现小幅度下降趋势；由图4的局部放大图可以看出，变点分布区间内的可靠度函数值下降速度变缓，且可靠度函数值下降速率远小于第一阶段末端200 h内的下降速率，这是因为减速器经过了磨合期，即浴盆曲线［27］的早期故障时期，减速器的传动精度得以小幅回升。

为了验证本文方法的有效性与适用性，以RV减速器传动精度退化数据为例，引用文献［19］中考虑变点的两阶段Wiener退化模型为参考，为了方便，记本文中模型为M0，文献［19］中的模型为M1，模型M1的全部参数估计结果见表5。

为了进一步直观地对比两种模型的可靠性建模效果，两种模型的减速器可靠度函数曲线对比見图5。可以看出，两种模型得到的减速器可靠度曲线趋势大体相同，但模型M0相比模型M1利用了变点分布区间，更平缓地过渡了一、二阶段退化过程，且可靠度函数曲线进入大幅度下降的时间相比模型M1更提前，这是因为考虑到了变点位置及每阶段测量误差的不确定性对模型的影响。

为了比较模型M0和模型M1的可靠度曲线拟合效果，给出了极大对数似然函数log-LF值和AIC值两个量化指标， AIC值的定义为

AIC=－2（log-LF）+2p（30）

其中，p为模型参数的个数，log-LF为模型的极大似然函数值。由AIC值的定义可知， log-LF越大、AIC值越小，模型的拟合效果越好。

表6给出了模型拟合的对数似然函数值（log-LF）和AIC值，可以看出，模型M0的log-LF值和AIC值均优于M1，说明模型M0对描述样本的两阶段退化过程有更好的拟合效果，在分析产品可靠性方面更准确。

为了进一步对比分析两种模型对RV减速器的寿命预测效果，分别采用模型M0和M1预测了减速器的平均寿命以及中位寿命、分位点寿命q0.5（0）、q0.1（0）、q0.5（3500）和q0.1（3500），结果见表7。可以看出，模型M0对RV减速器的寿命预测结果比M1更保守，这是因为模型M1假设各个样本变点位于同一测试时刻，未考虑变点位置的个体差异性，且忽视了测量误差的存在，而本文方法建立了两阶段的退化模型，不仅考虑到变点位置的个体差异性，还考虑了因为退化过程的不同会呈现出不同的测量误差。所以，采用模型M1的两阶段Wiener可靠性建模方法可能会导致危险的寿命预测结果，产品可能在预期的使用寿命前发生失效，从而可能影响到相关任务的顺利完成。

随机选取一组RV减速器传动精度退化数据，每隔500 h设置一个监测点，记录其精度退化量，利用本文计算失效概率密度函数和寿命预测的方法模拟出本文模型和考虑变点的两阶段模型在各个监测点的剩余寿命概率密度函数，与产品在各个监测点的真实寿命数据进行比较，得出两种模型对产品剩余寿命预测的准确程度。模型M0和M1在RV減速器传动精度退化数据下的剩余寿命概率密度函数和剩余寿命预测结果见图6。

由图6可以看出，两种模型的剩余寿命概率密度函数都能覆盖目标产品的剩余寿命真实值，且两种模型的剩余寿命概率密度函数随着时间的推移逐渐变窄，说明预测的不确定性越来越小，但本文模型的剩余寿命概率密度函数曲线在每一个监测点相比模型M1更加窄而尖锐，有助于减少预测结果的不确定性，在寿命预测方面具有更高的精度。为了进一步量化两种模型的预测结果，本文采用可靠性领域常用的性能指标：绝对误差（absolute error， AE）和相对误差（relative error， RE）指标来比较两种模型预测剩余寿命的准确程度。

两种模型剩余寿命预测的绝对误差见图7，可见，在设备运行的初始阶段，剩余寿命的估计值与剩余寿命的真实值之间有一定的偏差，这是由于产品的历史寿命数据较少而导致的不准确，而随着设备的运行，监测的运行数据不断增加，剩余寿命的估计值不断向剩余寿命真实值逼近，即估计精度不断提高。模型M0在各个监测时刻的绝对误差始终小于模型M1，其预测结果更为精确。

两种模型不同监测点相对误差比较结果见表8，可以看出在不同监测点，模型M0的相对误差均小于模型M1的相对误差，本文方法可以有效减少剩余寿命预测的相对误差，进而提高剩余寿命预测的精度，尤其在设备运行的最后监测时刻，本文方法剩余寿命预测的相对误差仅4.7％。综上，本文模型相比传统的两阶段Wiener退化模型在产品可靠性评估和寿命预测方面的平均精度提高了5.94%，具有更好的预测能力。

综上所述，本文模型不仅充分考虑了产品的退化特点，而且考虑了测量误差和变点对退化模型的不确定性，能够提高产品的可靠性寿命预测精度，具有一定的适用性，可为产品的维修、替换等提供理论依据。

4 结论

（1）在退化建模中引入不同阶段的测量误差，利用极大似然估计法和多维搜索算法结合得到了测量误差的估计值，考虑了每阶段的测量误差对可靠性建模的不确定影响，提高了建模的精度。

（2）多阶段退化过程中会出现变点，因为产品个体的差异性，变点可能会出现在不同的测试时刻之间，在考虑测量误差对建模不确定性的前提下也考虑了变点位置的不确定性，利用BIC最小准则和SSE最小准则相结合，合理地估计出变点的位置，提高了变点估计的准确性。

（3）考虑到变点位置的个体差异性，利用正态分布3σ原则确定了变点分布区间，给出了基于变点分布区间的分段可靠性分析方法，提高了产品的可靠性评估和寿命预测的精度。

本文方法在性能退化建模中考虑了测量误差及变点位置的个体差异性对退化建模的不确定性影响，但对于性能退化过程随着时间变化有着固有不确定性的产品，还可以引入自适应漂移项等指标，实现对模型参数的自适应估计和在线更新；考虑时变效应等多元不确定性对产品可靠性建模和寿命预测的影响，基于多元参数实现对产品可靠性的评估和剩余寿命的预测，这样就能更好地评估产品的可靠性。多元不确定性对退化建模的影响涉及多个变量之间的相关性计算，有待进一步研究。

参考文献：

［1］盛秀婷. 国内工业机器人可靠性研究综述［J］. 电子产品可靠性与环境试验， 2017， 35（6）：58-61.

SHENG Xiuting. Review on Reliability Research of Industrial Robots in China［J］. Reliability and Environmental Test of Electronic Products，2017， 35（6）：58-61.

［2］吴锦辉， 陶友瑞. 工业机器人定位精度可靠性研究现状综述［J］. 中国机械工程， 2020， 31（18）：2180-2188.

WU Jinhui， TAO Yourui. Review on the Research Status of Positioning Accuracy Reliability of Industrial Robots［J］. China Mechanical Engineering， 2020， 31（18）：2180-2188.

［3］张云， 于广， 王立平， 等. 基于性能退化数据的数控转台单子样可靠性分析［J］. 清华大学学报（自然科学版）， 2020， 60（4）：299-305.

ZHANG Yun， YU Guang， WANG Liping， et al. Reliability Analysis of Single Sample of NC Turntable Based on Performance Degradation Data［J］. Journal of Tsinghua University （Natural Science Edition）， 2020， 60（4）：299-305.

［4］PAN G， LI X， LUO Q， et al. A Reliability Evaluation of Marine Power Electronic Devices Based on Performance Degradation Data and a Competitive Failure Model［J］. Journal of Coastal Research， 2020， 105（s1）：67-70.

［5］王新刚， 张鑫垚， 杨禄杰， 等. 竞争失效条件下针对磨损退化数据的刀具可靠性分析［J］. 中国机械工程， 2020， 31（14）：1672-1677.

WANG Xingang， ZHANG Xinyao， YANG Lujie， et al. Tool Reliability Analysis for Wear Degradation Data under Competitive Failure Condition［J］. China Mechanical Engineering， 2020， 31（14）：1672-1677.

［6］WU J， YAN S， LI J， et al. Mechanism Reliability of Bistable Compliant Mechanisms Considering Degradation and Uncertainties：Modeling and Evaluation Method［J］. Applied Mathematical Modelling， 2016， 40（23/24）：10377-10388.

［7］YE Z S， XIE M. Stochastic Modelling and Analysis of Degradation for Highly Reliable Products［J］. Applied Stochastic Models in Business and Industry， 2015， 31（1）：16-32.

［8］陳志军， 李海波， 胡彦平. 基于随机维纳过程的结构损伤寿命预测与可靠性评估方法［J］. 南昌航空大学学报（自然科学版）， 2021， 35（1）：14-21.

CHEN Zhijun， LI Haibo， HU Yanping. Structural Damage Life Prediction and Reliability Evaluation Method Based on Stochastic Wiener Process［J］. Journal of Nanchang Aviation University （Natural Science Edition）， 2021， 35（1）：14-21.

［9］HONG L， YE Z S， KARTIKA S J. Interval Estimation for Wiener Processes Based on Accelerated Degradation Test Data［J］. IISE Transactions， 2018， 50（12）：1043-1057.

［10］WANG X， WANG B X， WU W， et al. Reliability Analysis for Accelerated Degradation Data Based on the Wiener Process with Random Effects［J］. Quality and Reliability Engineering International， 2020， 36（6）：1969-1981.

［11］WHITMORE G A. Estimating Degradation by a Wiener Diffusion Process Subject to Measurement Error［J］. Lifetime Data Analysis， 1995， 1（3）：307-319.

［12］PENG C Y， TSENG S T. Statistical Lifetime Inference with Skew-Wiener Linear Degradation Models［J］. IEEE Transactions on Reliability， 2013， 62（2）：338-350.

［13］王玺， 胡昌华， 任子强， 等. 基于非线性Wiener过程的航空发动机性能衰减建模与剩余寿命预测［J］. 航空学报， 2020， 41（2）：11-18.

WANG Xi， HU Changhua， REN Ziqiang， et al. Aeroengine Performance Degradation Modeling and Residual Life Prediction Based on Nonlinear Wiener Process［J］. Journal of Aeronautics， 2020， 41（2）：11-18.

［14］代毅， 成庶， 甘沁洁， 等. 基于线性Wiener过程的Ni-Cd蓄电池寿命预测［J］. 中南大学学报（英文版）， 2021， 28（9）：2919-2930.

DAI Yi， CHENG Shu， GAN Qinjie， et al. Life Prediction of Ni-Cd Battery Based on Linear Wiener Process［J］. Journal of Central South University， 2021， 28 （9）：2919-2930.

［15］TANG S， YU C， SUN X， et al. A Note on Parameters Estimation for Nonlinear Wiener Processes with Measurement Errors［J］. IEEE Access， 2019，7：176756 - 176766.

［16］黃亮， 刘君强， 贡英杰. 基于Wiener过程的发动机多阶段剩余寿命预测［J］. 北京航空航天大学学报， 2018， 44（5）：1081-1087.

HUANG Liang， LIU Junqiang， GONG Yingjie. Multi-stage Residual Life Prediction of Engine Based on Wiener Process［J］. Journal of Beijing University of Aeronautics and Astronautics， 2018， 44（5）：1081-1087.

［17］KONG D， BALAKRISHNAN N， CUI L. Two-phase Degradation Process Model with Abrupt Jump at Change Point Governed by Wiener Process［J］. IEEE Transactions on Reliability， 2017， 66（4）：1345-1360.

［18］董青， 郑建飞， 胡昌华， 等. 基于两阶段自适应Wiener过程的剩余寿命预测方法［J］. 自动化学报， 2022， 48（2）：15-22.

DONG Qing， ZHENG Jianfei， HU Changhua， et al. Residual Life Prediction Method Based on Two-stage Adaptive Wiener Process［J］ Journal of Automation， 2022， 48（2）：15-22.

［19］鄢伟安， 宋保维， 段桂林， 等. 基于两阶段维纳退化过程的液力耦合器可靠性评估［J］. 系统工程与电子技术， 2014， 36（9）：1882-1886.

YAN Weian， SONG Baowei， DUAN Guilin， et al. Reliability Evaluation of Hydraulic Coupling Based on Two-stage Wiener Degradation Process［J］. Systems Engineering and Electronic Technology， 2014， 36（9）：1882-1886.

［20］AGRAWAL G P， DUTTA N K. Semiconductor Lasers［M］. Berlin：Springer Science & Business Media， 2013.

［21］PRAKASH G， KAUSHIK A. A Change-point-based Wiener Process Degradation Model for Remaining Useful Life Estimation［J］. Safety and Reliability， 2020， 39（3/4）：44-62.

［22］GAO H， CUI L， DONG Q. Reliability Modeling fora Two-phase Degradation System with a Change-point Based on a Wiener Process［J］. Reliability Engineering & System Safety， 2020， 193：106601.1-106601.9.

［23］AKAIKE H. A New Look at the Statistical Model Identification［J］. IEEE Transactions on Automatic Control， 1974， 19（6）：716-723.

［24］NEATH A A， CAVANAUGH J E. The Bayesian Information Criterion：Background， Derivation， and Applications［J］. Wiley Interdisciplinary Reviews：Computational Statistics， 2012， 4（2）：199-203.

［25］LIU W， WANG X， LI S， et al. Study on the Effect of Failure Threshold Change Rate on Product Reliability Based on Performance Degradation［J］. Journal of Failure Analysis and Prevention， 2020， 20（2）：448-454.

［26］周坤， 叶楠， 吴锦辉， 等. RV减速器高应力加速退化试验及可靠性分析［J］. 哈尔滨工业大学学报， 2022， 54（7）：37-44.

ZHOU Kun，YE Nan，WU Jinhui， et al. High Stress Accelerated Degradation Test and Reliability Analysis of RV Reducer［J］. Journal of Harbin Institute of Technology， 2022， 54（7）：37-44.

［27］龙哲， 申桂香， 张英芝， 等. 基于浴盆曲线的数控机床早期故障试验时间研究［J］. 机床与液压， 2017， 45（11）：175-178.

LONG Zhe， SHEN Guixiang， ZHANG Yingzhi， et al. Research on Early Failure Test Time of NC Machine Tool Based on Bathtub Curve［J］. Machine Tools and Hydraulics， 2017， 45（11）：175-178.

（编辑 陈 勇）

作者简介：

高 新，男，1996年生，硕士研究生。

叶 楠（通信作者），男，1986年生，讲师。研究方向为工业机器人及核心零部件可靠性、结构动态力学性能等。E-mail：yenan@hebut.edu.cn。

收稿日期：2022-05-31

基金项目：国家重点研发计划（2017YFB1301300）；河北省教育厅基金重点项目（ZD2020180）