基于样条逼近的全站仪测量误差自动识别研究

何厚学

（甘肃铁道综合工程勘察院有限公司，甘肃 兰州 730000）

0.引言

全站仪测距比同层次测量仪器测距更长，在提升操作便利性的同时也能够保证测量工作效率。但全站仪测量容易受到测量环境干扰，从而对全站仪测量精度产生影响。因此，需要对全站仪测量误差识别，以便于后续纠正错误，降低全站仪测量误差造成的损失。

国外对于全站仪测量误差自动识别的研究，尚停留在对全站仪测量仪器的维护上，仅就数据观测中的误差及环境影响做统计，缺少对全站仪导线测量的主要误差源研究。国内图像识别技术较为成熟，能够对测量误差予以精确识别分析。正因如此，国内对全站仪测量误差的研究范围较广，涉及全站仪损坏误差、对中偏心误差及测距误差，其中横轴与竖轴的垂直误差为全站仪测量误差识别的主要内容，这也是目前针对全站仪测量误差研究的主要方向：利用基坑水平位移，对全站仪极坐标检测，同时分析误差并合理控制。

文献[7]中，结合三角高程测量的原理对全站仪测量阐述，通过对工程的测量确定全站仪三角高程测量的过程，对比普通水准测量说明全站仪测量的优点，测量应用缺少对全站仪测量误差的计算。

文献[8]中，根据全站仪测量使用方法总结全站仪的测量原理，对全站仪测量精度的策略制定，以此提高全站仪煤矿测量工作效率，虽然全站仪的测量效率得到提高，但测量过程操作规范度不够，导致测量误差增大。

文献[9]中，对全站仪的测量记录功能说明，对全站仪测量工程的精度单位计算，通过高斯平面校正投影边长，使得矿山测量工程进展流程加快，保证全站仪测量工程的贯通性，但高斯平面校正投影存在大气折射误差。

文献[10]中，对全站仪自由设站的测量工作分析，通过高精度全站仪三角高程测量，设计高程测量误差传播公式，根据公式计算测量误差和大气折光系数，以此为基础提高全站仪水准测量精度。但这种方法存在观测棱镜偏移。

本文通过样条逼近技术布设交叉测量网络，以测量网络为测量平面建立坐标系，计算全站仪测量误差特征向量，规范测量操作过程，在计算大气折射误差的同时，使得全站仪观测棱镜始终保持在中心位置上，为避免因导向边长相差过大引起误差，需保证全站仪观测导线边长相等。

1.基于样条逼近的全站仪测量误差自动识别方法设计

1.1 计算全站仪测量误差特征向量

对测量误差自动识别前，需要识别误差特征向量，因此要对全站仪测量误差特征向量计算。（如图1所示）在测量物体表面设置数个固定测点。测点分别为（M1，M2，…，Mn），n≥4，设置固定测量的垂足点为（M1′，M2′，…，Mn′），由此求得固定测点到垂足点的距离为（M1M1′，M2M2′，…，MnMn′），设测量物体表面到垂足点的距离为r，由此得到该距离条件为r＝。计算距离条件为r的全站仪固定测距向量，得到测距向量的集合为，…，。因此，计算得轴线向量的垂直条件，如公式（1）所示：

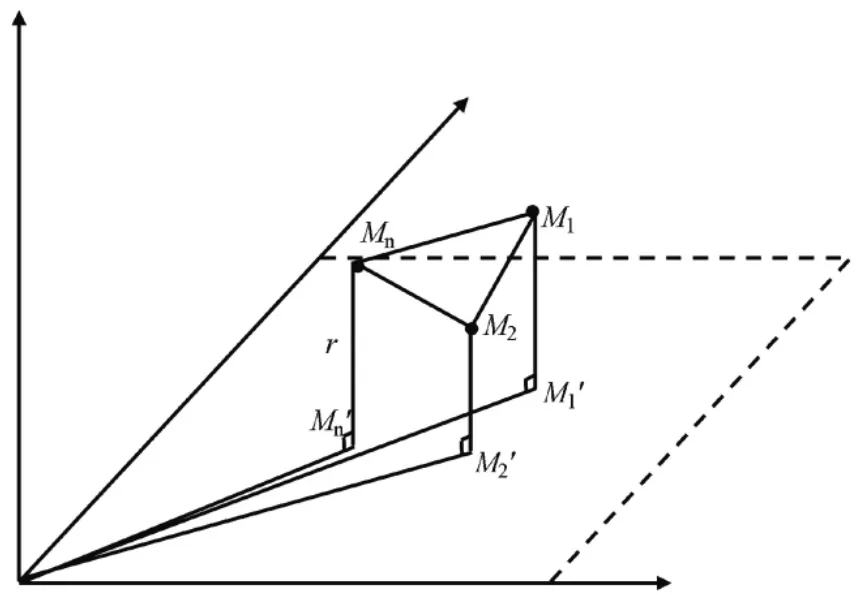
图1 全站仪测量误差特征向量数据

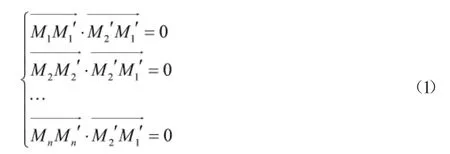
据此，得到全站仪测量固定的共线条件，为轴线上四个垂足的距离相等，即。

测量固定共线条件中常见线性函数，设固定测点的观测值误差为（m1，m2，…，mn）。独立观测值与观测函数值并不相等，由此得到误差mz在函数z中计算公式，如公式（2）所示：

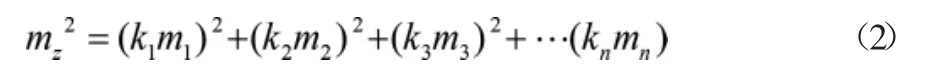
式（2）中，（k1，k2，k3，…，kn）为对应固定测点误差值（m1，m2，…，mn）的倍率系数，设全站仪独立观测函数z的表达式如公式（3）所示：

式（3）中，（x1，x2，…，xn）为函数总的处理观测值，独立观测函数对应的误差值为（m1，m2，…，mk），利用真差关系处理对应观测值与函数值，得到函数的全微分表达式，如公式（4）所示：

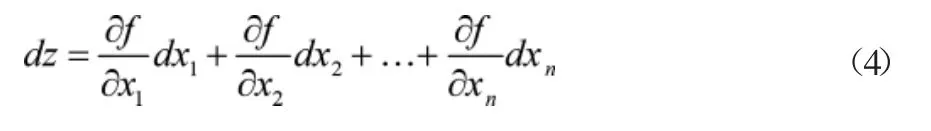
对独立观测函数全微分表达式做真差处理，得到真差替代处理后的关系表达式如公式（5）所示：

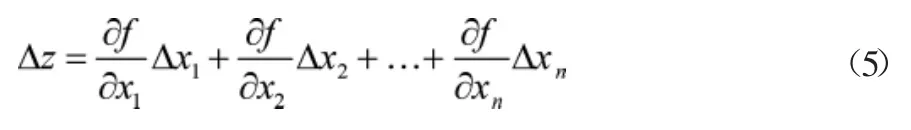
式（5）中，独立观测函数对xi的偏导数可以表示为（i＝1，2，…，n），确定观测值与函数式，将偏导数整理为常数的形式，将误差计算公式与偏导数建立关系，得到公式（6）所示：

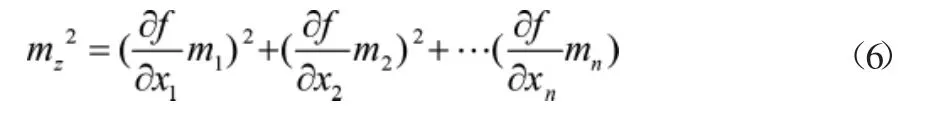
利用公式中的函数中误差，计算全站仪测量误差特征向量，表达式如公式（7）所示：

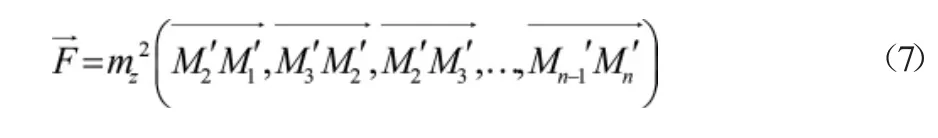
根据全站仪测量误差的特征向量，分别确定对应观测值的误差值，根据全站仪测量误差特征向量，设计全站仪测量误差自动识别算法。

1.2.设计全站仪测量误差自动识别算法

利用全站仪测量误差特征向量，制定全站仪测量误差特征标签。收集全站仪测量误差特征向量标签中的信息，对类似的特征向量信息予以存储，以此作为方向设计测量误差自动识别算法。

整合测量误差特征向量到同一个训练集中，并设置训练集的标签。（如图2所示）将全站仪测量误差特征向量转换为空间直角三维向量。以方差阵的形式设计每个角度方向的向量表达式B＝［β α］T，其中，T为全站仪测量训练集合维度，得到协方差的空间直角三维向量计算，如公式（8）所示：

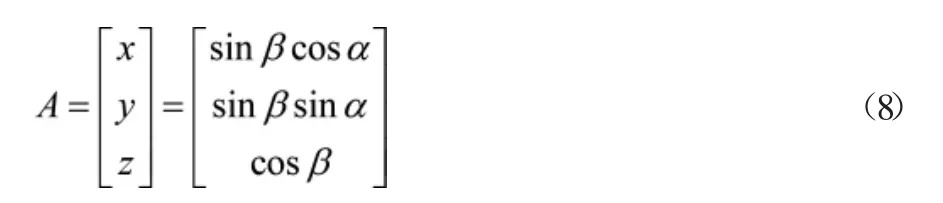
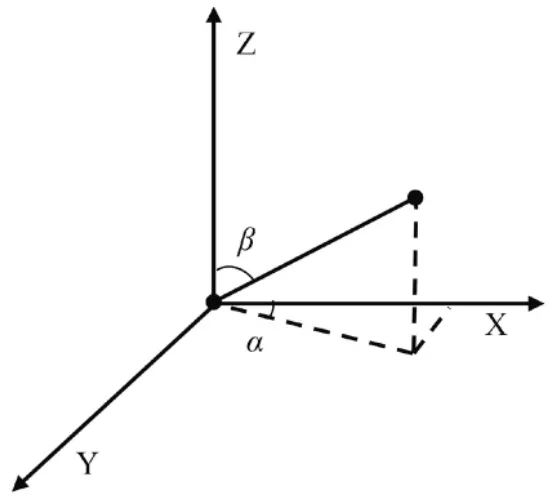
图2 坐标转换为空间直角三维向量

利用判断全站仪测量误差协方差的空间直角三维向量，确定全站仪测量误差分量识别内容，设全站仪测量误差出现的次数为n，针对测量误差识别特征点xi重复测量，并对比测量标准偏差s（xi），由此得到全站仪测量误差的识别平均值为s（x）。设计全站仪测量误差的识别不确定度的计算，如公式（9）所示：

式（9）中，sj为全站仪测量误差的标准平均值；m为总测量次数，根据不确定度的来源识别合成测量误差的输出量，设Y为待测目标的测量误差结果，整合识别的测量误差输入量N＝［X1，X2，…，XN］，根据测量误差识别输入量与输出量之间的映射关系，得到线性函数Y＝f（X1，X2，…，XN），利用线性函数整理全站仪测量误差自动识别输出量与输入量，如公式（10）所示：

式（10）中，N为线性函数整理全站仪测量误差自动识别输入量个数，XN为识别测量误差输入量的末端值，据此得到全站仪测量误差的自动识别矢量公式，如公式（11）所示：

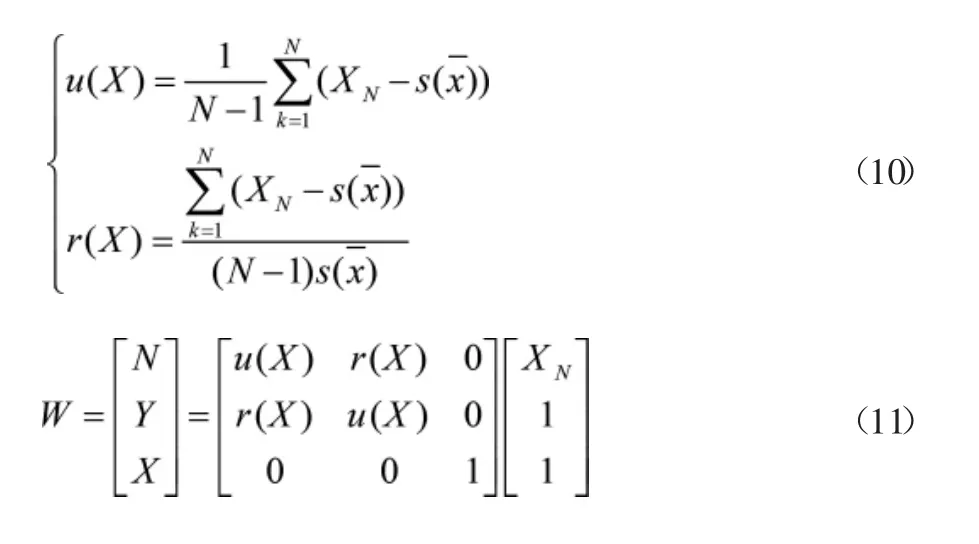
根据自动识别矢量公式中的单元结构参数，判断空间姿态的识别参数分量。对比分量中的分量常数及单元方向向量，确定全站仪测量误差自动识别的内容。根据全站仪测量自动识别内容，结合样条逼近技术构建自动识别模型，通过全站仪测量误差的自动识别相关性，对全站仪空间分量的测量误差识别。

1.3 构建样条逼近全站仪测量误差自动识别模型

根据全站仪测量误差自动识别算法，分配样条逼近全站仪测量误差自动识别的分量，据此给出相互独立的测量误差自动识别内容，通过输入映射核函数空间特征，实现非线性间隔分类。

针对全站仪测量误差自动识别算法，设计测量误差损失函数，根据选择的不平衡测量参数，区分小类样本测量误差识别与训练集测量误差识别。构建全站仪测量最优参数集合，并据此设计全站仪测量误差识别增长序列g＝2－15，2－13，…，23，设为全站仪测量误差自动识别修正值，则识别误差观测点间的距离如公式（12）所示：

式（12）中，K为样条逼近测量误差的修正集合，即K＝［K1，K2，K3］，转换得到识别误差修正集合的常数矩阵，利用修正集合中的常数项，对误差观点间距离计算识别向量的方差阵予以表达，如公式（13）所示：

设全站仪测量误差自动识别中的测点坐标为T＝［x0，y0，z0］，根据误差识别测点坐标表达方差阵方向向量，利用测得的全站仪向量方差阵对误差特征予以表达。设定特定的全站仪测量误差自动识别阈值，以阈值为限确定样条逼近的全站仪测量误差的识别结果，判断全站仪测量误差的识别拟合结果，对向量中的拟合维度判断。利用曲线逼近的辨别临界滑动面，判断全站仪测量误差自动识别的特征误差拟合，以此为基础对样条曲线重构，压缩并控制观测点。利用渐进迭代逼近的方法，对测量扩展曲线识别。以此完成对样条逼近全站仪测量误差自动识别模型的构建。

利用构建的样条逼近全站仪测量误差自动识别模型，确定全站仪测量误差自动识别的向量维度，根据维度中测量误差的特征，对应自动识别的测量误差指标，在确定模型的F1-measure小于常规值时，将测量误差的向量维度导入自动识别资料库中。根据资料库中全站仪测量误差维度，确定自动识别的填补项。并针对全站仪测量误差自动识别训练集，对全站仪测量误差特征分类，以确定自动识别对应的特征向量内容。对比特征向量内容与预定阈值大小，完成对全站仪测量误差的自动识别。

1.4 完成全站仪测量误差自动识别

利用全站仪测量误差自动识别模型，对全站仪测量误差自动识别。构建不同种类的全站仪测量误差识别标准，考虑到全站仪的测量视场范围较大，要确定角度仪器的修正范围，设定位瞄准的相关重复性误差系数为0.4，全站仪的自准分辨率在以0.01＂下，设全站仪测量误差自动识别中线坐标轨迹的计算，如公式（14）所示：

式（14）中，轨迹检测误差的测量值为g，则水平倾角在轨迹中线以外的测量误差识别，需要以全站仪测量误差独立坐标原点为中心，做坐标转换处理，如公式（15）所示：

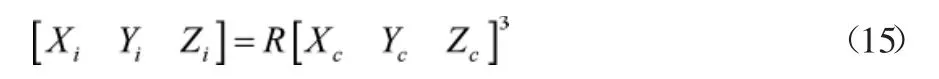
式（15）中，R为全站仪测量误差旋转矩阵，据测判断全站仪测量误差自动识别后的内积结果Z＝XiXc＋YiYc＋ZiZc。根据测量误差的自动识别内积结果设定测量误差外积处理内容，针对自动识别的内积设定结果计算测量误差自动识别的不确定度。

将全站仪测量误差自动识别的算法转换为矩阵乘法，根据全站仪视准轴的空间位姿确定不确定度的单元动态位姿，确定全站仪测量误差初始向量水平轴方向。得到样条逼近的全站仪测量误差自动识别不确定度的公式，如公式（16）所示：

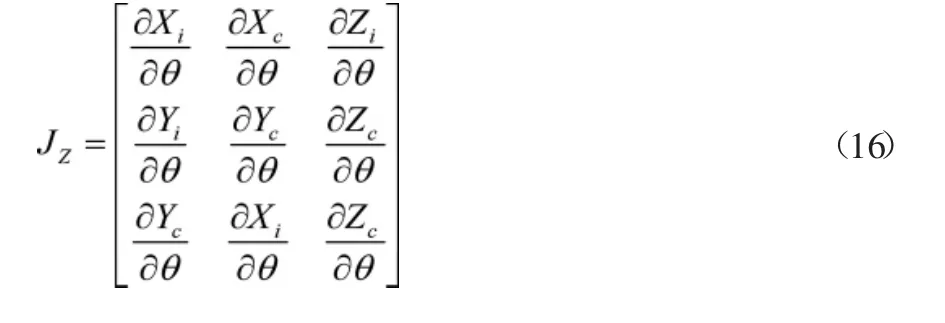
式（16）中，∂为全站仪测量误差的包含因子；θ为测量误差扩展角度，利用样条逼近的全站仪测量误差自动识别的不确定度，对样条逼近的全站仪测量误差计算，以此确定测量误差识别的矢量大小。根据置信概率重新构建自动识别误差矢量矩阵，得到自动识别测量误差的动态坐标（如图3所示）：

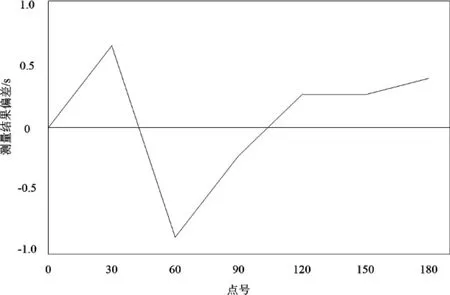
图3 自动识别测量误差的动态坐标

图3中，按照点号的顺序，对全站仪测量误差自动识别，识别结果自动生成折线，根据测量结果的偏差，对全站仪的测量误差计算。至此，完成对基于样条逼近的全站仪测量误差自动识别方法设计。

2.实验分析

为提高误差识别的速率，设计对比实验，对比数据分析识别法、二值化检测识别法、基于样条逼近的全站仪测量误差自动识别方法的测量误差识别SVN（SVN全名Subversion，即版本控制系统）检出量。

2.1.准备过程

应用全站仪对某目标进行测量，对全站仪测量现场中自动识别需要的基础数值（如图4所示）进行测量。

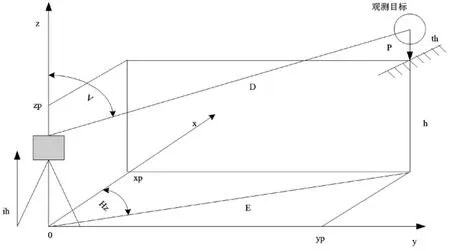
图4 全站仪自动识别基础数据采集示意图

处理图中的基础数据，根据观测目标到全站仪的距离D，确定观测目标的实际测量测距，E为全站仪到观测目标的实际距离；yp为观测目标到测量平面y的垂足；xp为观测目标到测量平面x的垂足；v和Hz分别为全站仪测量角度和观测目标；0为全站仪测量所在的坐标原点；P为观测目标所在的点；th为观测目标距离最短平面的距离；ih为全站仪观测平面到地面的距离。

整理好基础数据后，移动观测目标，并对上述基础数值进行移动后的测量，针对全站仪移动线路计算，得到全站仪测量误差自动识别的线路偏差结果（如图5所示）：

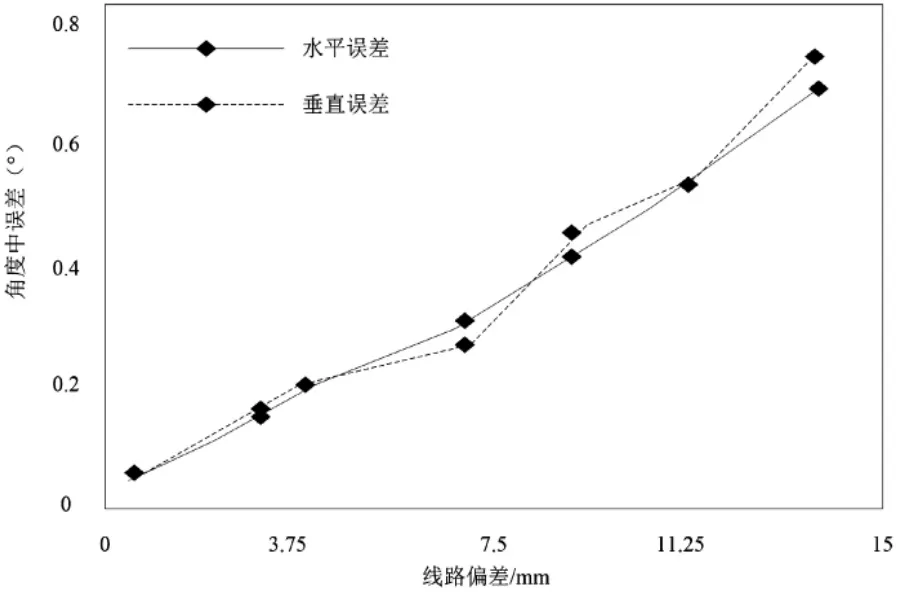
图5 全站仪测量误差自动识别的线路偏差结果

分析图中线路偏差结果可知：水平误差与垂直误差的线路偏差结果相近。由此可知线路测量选点操作与误差检出的线路偏差波动集中在3.75mm～7.50mm之间，为了保证线路偏差结果更接近测量误差标准，选择角度中误差在0.4°～0.6°的线路偏差区间作为实验测量内容。线路偏差区间中的测量误差数据分为10组。通过整理全站仪测量的自动识别测量结果，根据测量选点确定偏差波动的数据特征，针对上述数据特征做自动识别监测。针对全站仪测量误差自动识别中的水平误差与垂直误差做区分处理，分别计算线路偏差与角度中误差，由此整理得到十组测量误差识别SVN检出量。

2.2 分析结果

整理得到全站仪测量识别误差SVN检出量（如图6所示）：

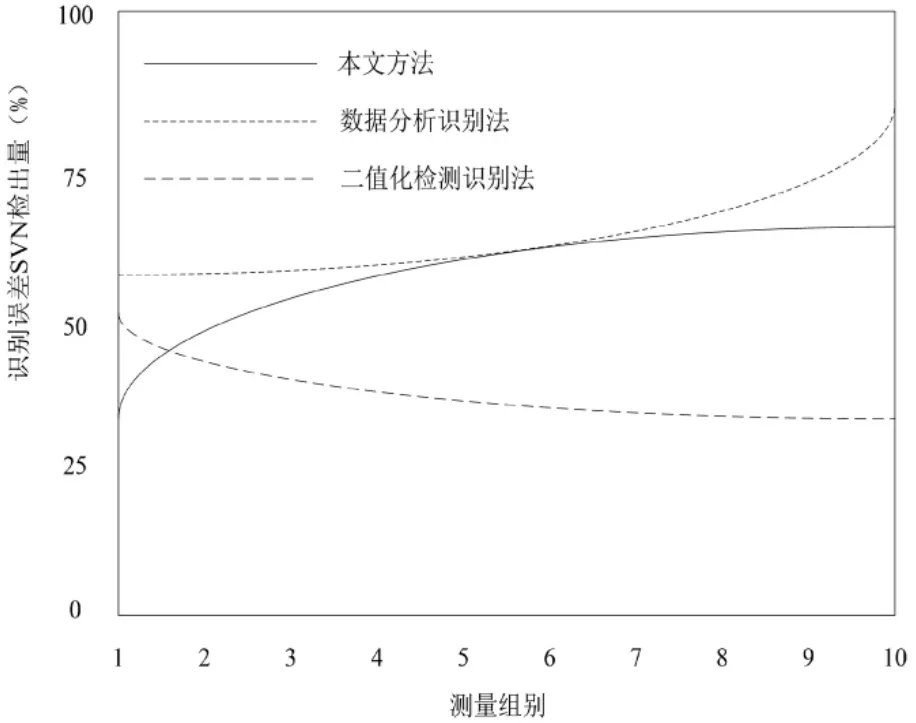
图6 测量误差自动识别前后的误差SVN检出量

由图6可知：数据分析识别法的全站仪测量识别误差SVN检出量在0.60以下，由于检出量受测量次数干扰逐渐趋于平稳，因此在后续的7～10组测量检出无明显变化，对后续测量结果的误差检出始终保持不变。可见应用数据分析识别法对全站测量误差的检出效果并不明显。

应用二值化检测识别法的全站仪测量识别误差SVN检出量在0.50以下，测量检出率在达到第7组时趋于平稳，整理测量识别检出率低于数据分析识别法。

应用基于样条逼近的全站测量误差自动识别方法，全站测量误差自动识别前后的误差SVN检出量在前几组保持稳定，处于0.60左右，在第5组测量检出结果后，误差SVN检出量明显上升，在第10组达到检出最高为0.88。因此，基于样条逼近的全站仪测量误差自动识别方法更优异。

3.结束语

通过本文研究，提高了全站仪测量误差自动识别的检出量。构建样条逼近全站仪测量误差自动识别模型，为全站仪测量误差自动识别提供基础数据。今后应继续研究提高全站仪测量精度，制定全站仪的测量识别指标，以此为基础建立基坑水平位移测量模型，利用测绘的空间地理信息提高全站仪的利用率。