机翼蒙皮铺层顺序和材料布局协同优化

彭翔　江浩浩　郭玉良　李吉泉　易兵　姜少飞

摘要：为了实现机翼蒙皮的轻量化和减振设计，将混杂复合材料引入到机翼蒙皮中，提出了机翼蒙皮铺层顺序和材料布局协同优化设计方法。将机翼蒙皮的铺层顺序和材料布局作为优化设计变量，建立了以成本为约束，蒙皮质量和位移最小化、频率最大化为目标的协同优化模型，利用搭建的通用化机翼蒙皮优化设计框架，使用非支配排序遗传算法-Ⅱ（NSGA-Ⅱ）实现了蒙皮内部结构的优化设计。与铝合金机翼蒙皮、初始结构方案蒙皮的性能对比表明，协同优化后的机翼蒙皮结构在不增加成本的条件下，综合性能显著提高，验证了方法的有效性。

关键词：混杂复合材料；多目标优化；机翼蒙皮；非支配排序遗传算法

中图分类号：TG156

DOI：10.3969/j.issn.1004-132X.2023.12.004

Collaborative Optimization of Stacking Sequence and Material Distribution for Wing Skins

PENG Xiang JIANG Haohao GUO Yuliang LI Jiquan YI  Bing JIANG Shaofei1，2

Abstract： To realize the lightweight and shock absorption design of the wing skins， the hybrid composite materials were introduced into the design of wing skins， and a collaborative optimization design method of stacking sequences and materials distribution was proposed for wing skins. The stacking sequences and material distribution of the wing skins were taken as the optimization design variables， the collaborative optimization model with cost as constraint， minimization of skin mass and displacement， and frequency maximization as objectives was established. The multi-objective collaborative optimization problem of the wing skins was carried out by using the NSGA-Ⅱ based on the developed optimization design framework of the wing skins. Compared with the performance of aluminum alloy wing skins and initial structure scheme， the optimized stacking sequences and material distributions may significantly improve the comprehensive performance of the wing skins without increasing the costs， which verifies the effectiveness of the proposed method.

Key words： hybrid composite； multi-objective optimization； wing skin； non-dominated sorting genetic algorithms-Ⅱ（NSGA-Ⅱ）

0 引言

機翼蒙皮是直接承受飞机气动载荷的主要承力部件［1-3］，减小机翼蒙皮质量，提高机翼蒙皮的强度和振动特性，实现轻质、高强、高效的蒙皮结构优化设计［4-5］，是提高飞机飞行效率、改善飞机综合性能的有效手段。

飞机机翼常见的蒙皮有金属蒙皮、复合材料蒙皮、整体壁板等。纤维增强复合材料具有比强度高、比模量大等优点，逐渐取代了金属材料的地位［6-7］，在机翼蒙皮结构中应用越来越广泛。复合材料结构在提高机翼蒙皮性能、减小机翼蒙皮质量和减少成本等方面的贡献越来越突出。由于机翼蒙皮结构实际工况复杂，需要满足低成本、高强度、多工况等多目标设计需求，因此采用单一复合材料往往难以实现多目标的综合最优，引入由多种复合材料组成的混合复合材料，通过多复合材料优势的综合互补，固有频率［8-9］、弯曲应力和弹性模量比［10-11］等均会有所提高，因此，进行基于混合复合材料的机翼蒙皮结构设计，对改善蒙皮结构、提高机翼性能和飞机综合性能具有很好的工程意义和发展前景［11］。

机翼蒙皮的层间铺层顺序对蒙皮性能具有较大的影响［12］，固定的铺层顺序难以实现最佳的方案设计。GHIASI等［13-14］根据蒙皮等复合结构的尺寸差异，将铺层顺序优化问题分为恒定刚度和变刚度两类，并进行了详细分析。YU等［15］进行了以基频最大化为目标的铺层顺序优化，提高了复合结构的强度。RAJPAL等［16］通过铺层顺序优化，改善了机翼结构的抗阵风和疲劳载荷冲击性能。

由于机翼蒙皮的结构复杂性和高性能需求［17］，进行单目标的铺层优化难以满足蒙皮性能需求，开展机翼蒙皮结构的多目标协同优化才能实现综合性能最优。GUO等［18］进行了机翼蒙皮的铺层顺序和铺层厚度协同优化，在满足气动载荷的同时，将某型号飞机机翼蒙皮结构的质量减小了30%。SHRIVASTAVA等［19］将某型号飞机翼面材料替换为碳纤维复合材料，并进行了蒙皮铺层方向优化，提高承载能力的同时将蒙皮质量减小了12%。CHOI等［20］研究了柔性机翼蒙皮的铺层厚度、后掠角、锥度比的变化对复合材料机翼结构的最大续航能力和结构质量的影响，最终在飞机续航能力增大20.9%的条件下，机翼质量减小了5.4%。此外，SCARDAONI等［21］提出了一种两级多尺度优化策略，通过机翼翼盒不同区域的铺层顺序、厚度的协同优化，使得翼面整体质量减小30%，强度提高16%。

虽然国内外学者提出了大量蒙皮结构优化设计方法，有效减小了机翼蒙皮质量，但是以往研究主要针对单材料下的蒙皮结构，难以满足质量、成本、性能等多方面的综合性能要求。本文将混杂复合材料引入到机翼蒙皮设计中，提出一种铺层顺序和材料布局协同优化的方法，实现机翼蒙皮结构的成本、质量、一阶频率的多目标协同优化，有效改善机翼蒙皮结构性能，并对结果进行对比，验证方法的有效性。

1 机翼蒙皮优化问题描述

1.1 混杂复合材料机翼蒙皮优化问题

相较于单一复合材料组成的机翼蒙皮结构（图1a），混杂复合材料构成的机翼蒙皮结构（图1b）可以充分利用不同复合材料的优势，实现多性能的综合最优。将机翼蒙皮划分成6个区域，如图2所示，每个蒙皮区域有4种备选的复合材料，将机翼蒙皮的成本O作为约束条件，以机翼蒙皮结构的一阶振动频率ω最大化、气动载荷下的位移U和机翼蒙皮质量G最小化作为优化目标，进行铺层顺序θ以及6个区域的材料布局方案χ的协同优化。

构建的机翼蒙皮结构优化目标函数如下：

其中，θi为第i层的铺层角度，θi∈θ={－45°，0°，45°，90°}；χj为第j个区域选择的材料，χj∈χ={1，2，3，4｝；Vj为机翼蒙皮第j个区域的体积；ρd为第d种备选材料的密度；Cd为第d种材料的单位成本；为成本约束条件。优化目标函数G和成本函数O是关于材料分布χ的函数；一阶频率ω和位移U是材料分布χ和铺层顺序θ的函数。

1.2 机翼蒙皮结构性能计算

机翼蒙皮表面受到升力L和阻力T的作用，如图3所示。作用于机翼蒙皮上的载荷主要分为直接作用在机翼蒙皮表面上的气动力分布载荷qa，分布在整个机翼结构上的质量力和安装在机翼上的成品设备、燃油的分布质量力qc，以及与机翼连接的其他部件通过接头传递给机翼的力qb。机翼表面的载荷分布如图4所示，图中Qsec为切割的局部机翼面积气动合力。三类载荷引起的机翼承受的剪力F、力矩M和扭矩I［22］分别为

其中，c（d）fc、c（d）fg、c（d）m分别为碳纤维、玻璃纤维和基体的单位质量成本；ρ（d）fc、ρ（d）fg、ρ（d）m分别为碳纤维、玻璃纤维和基体的密度；v-（d）fc、v-（d）fg、v-（d）m分别为碳纤维、玻璃纤维和基体的体积含量，纤维和基体体积含量之和为1。

2 机翼蒙皮结构有限元分析

以某型号小型飞机机翼为研究对象，机翼的类型为单梁式。该翼型是矩形平直翼，机型的机翼前缘和后缘均为直线，且与飞机的纵轴线相互垂直。该机型的飞机在飞行时所受到的阻力较大，一般适合低速稳定的飞行，飞机的最大起飞质量为1150 kg，实用升限为5000 m，满载时的最大航程为944 km，飞机最大巡航速度为237 km/h，正常飞行巡航时的速度为203 km/h［25］。

由于机翼结构过于复杂，所以在利用ABAQUS有限元软件建模时，对模型进行了简化处理，将机翼模型简化为由17根翼肋、3对桁条、1个主翼梁和机翼蒙皮组成。图5所示为机翼的蒙皮结构，图6所示为机翼内部构造模型，图7所示为机翼的翼肋、桁条、翼梁和蒙皮总体组合结构。机翼的模型尺寸长为4.02 m、宽为1 m。

机翼蒙皮各区域候选的4种复合材料属性信息如表2所示。同时，为了降低整个制造过程的复杂性，假设每一区域各铺层备选材料都是同一种。

初始有限元分析条件下的机翼蒙皮每个区域有8个铺层且对称铺设，机翼蒙皮各铺层厚度值取0.2 mm，铺层顺序为［-45°/0°/45°/90°］s，蒙皮1～6区域的材料布局分别为材料0、材料1、材料2、材料3、材料0、材料1。在ABAQUS中蒙皮铺层堆叠顺序如图8所示，划分的6个区域在同一方案下的铺层顺序是相同的。

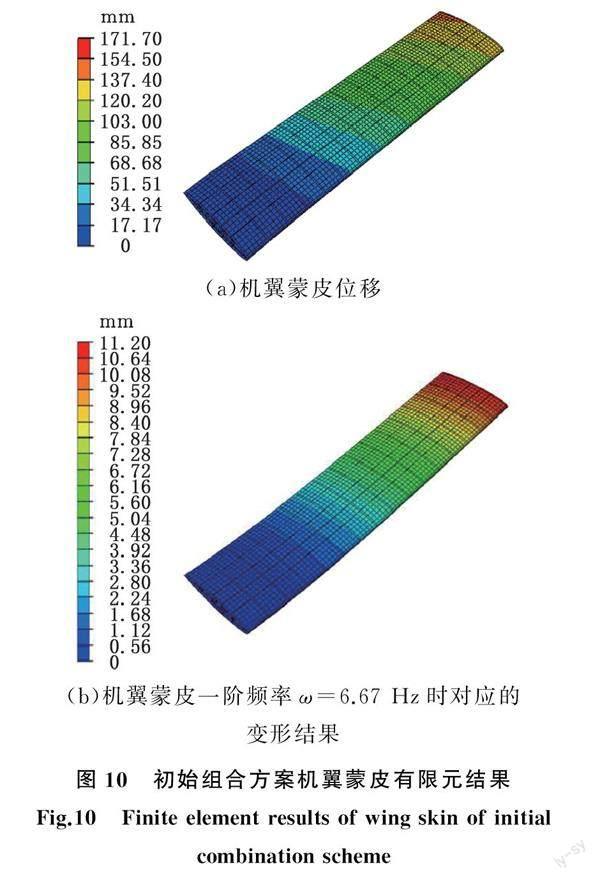
根据1.2节的受力分析，作用在机翼蒙皮表面的气动载荷在蒙皮的表面沿机翼展向和弦向呈近似梯度分布，将两个方向上分布的载荷拟合成载荷场，对机翼翼根处施加固定约束，如图9所示。在ABAQUS中将机翼蒙皮和骨架看成一个整体单元，骨架结构采用实体单元，蒙皮采用壳单元。在初始组合方案下，机翼蒙皮的位移、一阶频率和成本及质量分析结果如图10所示。机翼蒙皮结构在气动载荷作用下的位移为146.1 mm，蒙皮质量为20 830 g，一阶频率为6.67 Hz，成本为257.14 USD。从多目标分析结果来看，初始组合方案下的混杂复合材料机翼蒙皮结构的综合性能并不理想，还有很大的优化空间来进一步提升机翼蒙皮结构的综合性能，因此需要对机翼蒙皮结构各区域的混杂复合材料布局和铺层顺序组合方案进行优化，获得更优的组合设计。

3 优化分析

3.1 优化策略

机翼蒙皮的优化设计属于多目标优化问题，需要在满足成本约束的条件下，以机翼蒙皮结构的质量、位移和一阶频率为优化目标，使用非支配排序遗传算法-Ⅱ（non-dominated sorting genetic algorithms，NSGA-Ⅱ）对蒙皮铺层角度和各区域材料分布进行协同优化设计。在NSGA-Ⅱ优化设计算法中，通过初始化、计算适应度函数、变异与交叉运算、非支配排序和精英排序5个主要环节来实现优化目标。同时，NSGA-Ⅱ可以加快优化算法中的非支配排序过程，降低多目标优化模型的整体计算复杂度，使帕累托前沿朝着更加均匀的方向发展［26］。

在优化模型中，铺层顺序θ与材料分布方案χ都是离散变量，所以在优化设计中将使用离散整数值单独编码。对铺层顺序θ进行编码，用π1代表θ=0°，π2代表θ=45°，π3代表θ=-45°，π4代表θ=90°。对材料混杂方案χ进行编码，用数字0、1、2、3分别代表材料0、材料1、材料2和材料3。用X1、X2、X3、X4、X5、X6分别代表机翼蒙皮的6个优化区域。

基于NSGA-Ⅱ的机翼蒙皮结构优化基本流程如图11所示。该算法基于拥挤度比较算子的快速非支配排序算法获得机翼蒙皮铺层顺序θ与材料混杂方案χ的子代个体。非支配排序规则为：种群内的每个个体i都有两个属性wi和i，它们分别表示为种群中支配个体i的个体数量和被i支配的个体集合，对于wi=0的个体，保存在当前集合F1i中，对于当前集合F1i中的个体，它所支配的个体集合为，遍历中的每个个体i，执行wi←wi-1，如果wi=0，则将个体i保存到集合F2中，将F1i和F2分别记为第一和第二非支配层，重复上述操作直到整个种群被分级。拥挤度计算规则为：如果第i个个体满足成本约束要求，即h（i）1<=350 USD，則优化目标一阶频率ω、质量G和最大位移U的适应度函数记为ω（i）Λ、G（i）Λ和U（i）Λ，反之如果不满足约束，优化目标的适应度函数为ωminΛ、GminΛ和UminΛ，在2Θ个种群中产生的最小和最大目标函数的适应度函数为ωmaxΛ、ωminΛ、GminΛ、GmaxΛ、UminΛ、UmaxΛ，拥挤度为

其中，ψ表示优化目标函数的个数，Λ表示基于每个目标函数对所有个体进行升序排列，图11中的Rank=1，2…表示按照种群大小进行排序，fΛ为优化目标函数。通过对拥挤度距离排序选出排名较低的Θ个个体为下一代种群。如果父子代合并后产生新父代种群，则新父代种群通过选择、交叉和变异保留优质个体，并进入下一轮遗传迭代，在产生子代的过程中，铺层顺序θ和材料混杂方案χ将会根据确定的交叉概率和变异概率分别进行交叉、变异。之后，分析计算获得父代种群Pt与子代种群Qt中的2Θ个个体的相应目标函数值ω、G、U和成本函数值O。

通过不断重复上述迭代过程直到迭代次数达到120代时遗传结束，获得在竞争机制下保留的优质个体。

3.2 优化流程

为了能够快速实现机翼蒙皮结构在多目标下的协同优化设计，基于ISIGHT优化平台建立了图12所示的机翼蒙皮结构的协同优化分析求解框架。通过ISIGHT对ABAQUS、MATLAB、Date Exchanger以及Excel的集成，实现对机翼蒙皮的快速优化分析。对机翼蒙皮结构的性能分析是通过批处理文件驱动二次开发代码实现的，各模块之间的高效协调通过MATLAB指令实现。选用非支配排序遗传算法NSGA-Ⅱ对分析的机翼蒙皮模型参数不断迭代分析，并最终输出机翼蒙皮结构优化组合的最优帕累托解集。

3.3 优化方法验证

以长宽比为1.5的混杂复合材料层压板［27］为例，验证本文提出的多目标优化方法的有效性。进行T300/5028和Scotchply1002两种材料的铺层数量和铺层角度协同优化，优化目标为一阶频率最大化、质量和成本最小化，优化当中同时考虑铺层的制造要求，铺层角度变化值为-45°/0°/45°/90°，同时相同角度的铺层数量不能连续超过4层，每层厚度为0.125 mm，T300/5028的价格是Scotchply1002的8倍。表3列出了本文方法与文献［27］计算的优化结果，表中LT和LG分别表示T300/5028和Scotchply1002的铺层数量。结果显示两种方法获得的一阶频率、质量和成本接近，本文优化分析框架能够进行多材料铺层序列和材料布局的协同优化，验证了本文优化方法的有效性和可靠性。

3.4 优化结果分析

在对机翼蒙皮结构的多目标优化设计中，主要考虑了在成本约束的条件下三种不同的优化设计目标，分别是机翼结构的一阶频率、位移以及结构总质量。优化分析结果中，图13所示为机翼蒙皮结构的位移、一阶频率以及质量的目标值变化趋势，可以看出，位移及质量均在低位水平达到收敛，一阶频率在高位趋于平直，反映出较好的优化效果。

同时，考虑到铺层顺序、材料分布方式两个不同因素对机翼结构一阶频率特性、应力应变特性和机翼蒙皮结构质量的影响，通过上述机翼蒙皮优化分析流程，获得了图14所示的输入与输出变量的关联分析表，反映输入变量对各个优化目标的贡献程度。输入变量J1、J2、J3、J4分别表示机翼蒙皮每个区域的第一、二、三和第四铺层角度的变化，X1、X2、X3、X4、X5、X6分别表示划分的6块机翼蒙皮区域的材料布局变化。分析可知，J2和J3对机翼蒙皮结构一阶频率贡献最大，即机翼蒙皮结构的第二、三铺层顺序的变化对机翼蒙皮一阶频率影响最大；同时，对机翼蒙皮结构的成本和质量影响最大的是各蒙皮区域材料的布局，材料的选择对成本和质量影响较为显著；影响机翼蒙皮位移最大的是变量J2、J3和X5，机翼蒙皮第二、三铺层角度和蒙皮区域5种材料的选择是影响机翼蒙皮位移的关键因素。

由于3个优化目标无法进行统一的结果比较，因此为了从众多的非劣解中获得相对的最优解，需要对帕累托解集进行折中处理，获得由NSGA-Ⅱ多目标优化设计算法得到的帕累托前沿如图15所示。

在Isight中对获得的帕累托解集按照下式进行选优排序：

Φ=sum（WiRi）/Si（14）

其中，Ri为目标函数值，Wi为权重因子，Si为比例因子。权重因子和比例因子共同决定了目标函数的重要性。基于这些经验参数，对帕累托前沿进行处理，获得不同组合方案下的前15组参考最优解，如表4所示。

4 结果对比

在表4中获得15组帕累托最优解集，根据目标函数的权重和比例因子，通过式（14）计算得到多目标协同优化下的目标值，并对目标值进行排序，选择综合性能最优的一个组合方案。通过分析获得机翼蒙皮结构材料分布和铺层组合方案的最优解为［90°/45°/90°/-45°］s、{3 1 1 1 1 0}。同时，为比较金属机翼蒙皮结构与混杂复合材料蒙皮结构的差异，将优化后的结果与第2节初始组合方案、金属蒙皮的计算结果进行对比，表5、表6所示为三种情况下的数值分析结果，图16、图17为有限元云图对比，图18为三种情况下优化目标结果对比直方图。

由表6可以看出，优化之后机翼蒙皮的一阶固有频率从铝合金条件下的6.40 Hz提高到混杂复合材料条件下的9.14 Hz。根据仿真分析结果，只考虑该气动载荷工况（图9），机翼的外部激励共振频率最高为6.34 Hz（图19），优化之后可以有效远离载荷的共振频率区域，减少机翼共振。本文得到的9.14 Hz只针对本文使用的机翼结构及载荷情况。针对具体的实际机翼结构，可以运用本文提出的方法针对实际工况及载荷进行具体机翼蒙皮的结构优化设计。

利用搭建的机翼蒙皮结构优化分析流程，通过迭代计算获得了优化后的最优组合方案。相较于初始组合方案机翼蒙皮、铝合金机翼蒙皮下的有限元計算结果，一阶频率提高了约37%和42%，最大位移分别减小了约70%和77%，优化后的质量相较于初始组合方案下的蒙皮质量略微减小，但相较于铝合金机翼蒙皮质量约减小了45%。通过协同优化，在不提高成本的基础上能够进一步减小机翼蒙皮的质量、提高振动特性和强度特性，验证了方法的有效性。

5 结语

本文将混杂复合材料引入机翼蒙皮结构的优化设计中，提出了机翼蒙皮铺层顺序和材料布局协同优化方法。构建了综合考虑机翼蒙皮结构的质量、成本、最大位移、频率的多目标优化设计函数，基于NSGA-Ⅱ算法实现了混杂复合材料机翼蒙皮的结构优化。相较于初始组合方案机翼蒙皮、铝合金机翼蒙皮结构，改进蒙皮结构的一阶频率提高了约37%和42%，最大位移分别减小了约70%和77%，验证了方法的有效性。

本文着重从仿真分析与参数优化的角度进行了简单工况下的机翼蒙皮结构设计，后续将根据实际机翼蒙皮的复杂受载情况进行优化结果的精细化，并开展实物试验，以进一步验证提出的协同优化方法的有效性与实用性。

参考文献：

［1］LI Y， GE W， ZHOU J， et al. Design and Experiment of Concentrated Flexibility-based Variable Camber Morphing Wing［J］. Chinese Journal of Aeronautics， 2022， 35（5）：455-469.

［2］MA Y， KARPUK S， ELHAM A. Conceptual Design and Comparative Study of Strut-braced Wing and Twin-fuselage Aircraft Configurations with Ultra-high Aspect Ratio Wings［J］. Aerospace Science and Technology， 2022， 121：107395.

［3］周文雅，张宗宇，王晓明，等.機翼中小尺度主动变形研究进展及关键技术［J］. 机械工程学报，2021，57（2）：121-138.

ZHOU Wenya， ZHANG Zongyu， WANG Xiao-ming， et al. Research Progress and Key Technologies of Small and Medium Scale Active Deformation of Wings［J］. Journal of Mechanical Engineering， 2021，57（2）：121-138.

［4］陈迎春，张美红，张淼，等.大型客机气动设计综述［J］.航空学报，2019，40（1）：35-51.

CHEN Yingchun， ZHANG Meihong， ZHANG Miao， et al. A Review of Aerodynamic Design for Large Passenger Aircraft［J］. Acta Aeronautica et Astronautica Sinica， 2019， 40（1）：35-51.

［5］DATE S， ABE Y， OKABE T. Effects of Fiber Properties on Aerodynamic Performance and Structural Sizing of Composite Aircraft Wings［J］. Aerospace Science and Technology， 2022， 124：07565.

［6］ASYRAF M R M， ILYAS R A， SAPUAN S M， et al. Advanced Composite in Aerospace Applications：Opportunities， Challenges， and Future Perspective［M］∥Advanced Composites in Aerospace Engineering Applications.Springer， Cham， 2022：471-498.

［7］冯雁，郑锡涛，吴淑一，等.轻型复合材料机翼铺层优化设计与分析［J］.航空学报，2015， 36（6）：1858-1866.

FENG Yan， ZHENG Xitao， WU Shuyi， et al. Lightweight Composite Wing Layer Optimization Design and Analysis［J］. Acta Aeronautica et Astronautica Sinica， 2015， 36（6）：858-1866.

［8］PENG X， QIU C， LI J， et al. Multiple-scale Uncertainty Optimization Design of Hybrid Composite Structures Based on Neural Network and Genetic Algorithm［J］. Composite Structures， 2021， 262：13371.

［9］INNAMI M， HONDA S， SASAKI K， et al. Analysis and Optimization for Vibration of Laminated Rectangular Plates with Blended Layers［J］. Composite Structures， 2021， 274：114400.

［10］SAFRI S N A， SULTAN M T H， JAWAID M， et al. Impact Behaviour of Hybrid Composites for Structural Applications：a Review［J］. Composites， Part B：Engineering， 2018， 133：112-121.

［11］ALAM M A， YA H H， SAPUAN S M， et al. Recent Advancements in Advanced Composites for Aerospace Applications：a Review［J］. Advanced Composites in Aerospace Engineering Applications， 2022：319-339.

［12］BOHRER R Z G， KIM I Y. Concurrent Topology and Stacking Sequence Optimization of Composite Laminate Plates Using Lamination Parameters［J］. Composite Structures， 2021， 276：14556.

［13］GHIASI H， PASINI D， LESSARD L. Optimum Stacking Sequence Design of Composite Materials Part I： Constant Stiffness Design［J］. Composite Structures， 2009， 90（1）：1-11.

［14］GHIASI H， FAYAZBAKHSH K， PASINI D， et al. Optimum Stacking Sequence Design of Composite Materials Part Ⅱ：Variable Stiffness Design［J］. Composite Structures， 2010， 93（1）：1-13.

［15］YU S， YANG Y， COLTON J S. Improved Composite Open-hole Compression Strength and Trade-off with Manufacturability Controlled by Stacking Sequence Effect and Non-standard Ply Angles［J］. Composites， Part B：Engineering， 2022， 228：109410.

［16］RAJPAL D， MITROTTA F M A， SOCCI C A， et al. Design and Testing of Aeroelastically Tailored Composite Wing under Fatigue and Gust Loading Including Effect of Fatigue on Aeroelastic Performance［J］. Composite Structures， 2021， 275：114373.

［17］梁路，萬志强，杨超.大型飞机复合材料机翼壁板气动弹性优化设计［J］. 中国科学（技术科学）， 2012， 42（6）：722-728.

LIANG Lu， WAN Zhiqiang， YANG Chao. Aeroelastic Optimization Design of Large Aircraft Composite Wing Panel［J］. Chinese Science（Technology Science）， 2012， 42（6）：722-728.

［18］GUO S， LI D， LIU Y. Multi-objective Optimization of a Composite Wing Subject to Strength and Aeroelastic Constraints［J］. Proceedings of the Institution of Mechanical Engineers， Part G：Journal of Aerospace Engineering， 2012， 226（9）：1095-1106.

［19］SHRIVASTAVA S， MOHITE P M. Design and Optimization of a Composite Canard Control Surface of an Advanced Fighter Aircraft under Static Loading［J］. Curved and Layered Structures， 2015， 2（1）：91-105.

［20］CHOI W， PARK H. Optimized Design and Analysis of Composite Flexible Wing Using Aero-nonlinear Structure Interaction［J］. Composite Structures， 2019， 225：111027.

［21］SCARDAONI M P， IZZI M I， MONTEMURRO M， et al. Multi-scale Deterministic Optimisation of Blended Composite Structures：Case Study of a Box-wing［J］. Thin-walled Structures， 2022， 170：108521.

［22］杨伟，常楠，王伟.飞机复合材料翼面结构优化设计理论与应用［M］.北京：国防工业出版社，2014：7-20.

YANG Wei， CHANG Nan， WANG Wei. Aircraft Composite Wing Structure Optimization Design Theory and Application［M］. Beijing：National Defense Industry Press， 2014：7-20.

［23］马丁·西蒙斯.模型飞机空气动力学［M］. 肖治垣，马东立，译.北京：航空工业出版社，2007：101-130.

MARTIN Simmons. Model Aircraft Aerodynamics［M］. XIAO Zhiyuan， MA Dongli， trans. Beijing：Aviation Industry Press， 2007：101-130.

［24］沈觀林，胡更开，刘彬.复合材料力学［M］.北京：清华大学出版社， 2013：87-99.

SHEN Guanlin， HU Gengkai， LIU Bin. Composite Mechanics［M］. Beijing：Tsinghua University Press， 2013：87-99.

［25］段维翔，郝劲松. 飞机系统［M］. 成都：西南交通大学出版社， 2002：56-70.

DUAN Weixiang， HAO Jinsong. Aircraft System ［M］. Chengdu：Southwest Jiaotong University Press， 2002：56-70.

［26］VERMA S， PANT M， SNASEL V. A Comprehensive Review on NSGA-Ⅱ for Multi-objective Combinatorial Optimization Problems［J］. IEEE Access， 2021， 9：57757-57791.

［27］AN H， CHEN S， HUANG H. Multi-objective Optimal Design of Hybrid Composite Laminates for Minimum Cost and Maximum Fundamental Frequency and Frequency Gaps［J］. Composite Structures， 2019， 209：268-276.

（编辑 王艳丽）

作者简介：

彭 翔，男，1989年生，博士、副教授。研究方向为结构优化设计。E-mail：pengxiang@zjut.edu.cn。

李吉泉（通信作者），男，1977年生，教授、博士研究生导师。研究方向为结构优化设计。E-mail：lijq@zjut.edu。

收稿日期：2022-08-04

基金项目：国家自然科学基金（51875525）；浙江省自然科学基金（LY21E050008）