高锁螺母收口、装配及松动过程有限元分析

张京东　邓博　桂学文　李健　廖日东

摘要：针对UNJ螺纹高锁螺母开展了有限元建模方法研究，编写了可生成结构化网格的建模程序，并建立了精细的有限元网格模型。对高锁螺母的收口过程、装配过程及受到横向载荷下的松动行为进行了有限元仿真，并通过拧紧试验对仿真得到的锁紧力矩值进行了验证。仿真结果表明：在一定收口量范围内，高锁螺母的最大径向位移量以及锁紧力矩均与收口量近似满足线性关系，且随着收口量的增大，最大径向位移量与锁紧力矩均增大；高锁螺母的锁紧力矩越大对应防松性能越好，然而收口量对防松性能存在最優值，当收口量超过最优值后，继续增大收口量对防松性能的提升效果并不显著。

关键词：高锁螺母；收口；锁紧力矩；防松性能

中图分类号：V229

DOI：10.3969/j.issn.1004-132X.2023.12.001

Finite Element Analysis for Extrusion， Assembly and Loosening Processes of Hi-lock Nuts

ZHANG Jingdong DENG Bo GUI Xuewen LI Jian LIAO Ridong

Abstract： The FE（finite element） modeling method of UNJ threaded hi-lock nuts was investigated， and a modeling program was written to generate structured meshes， through which the fine FE meshed model was established. The extrusion process， assembly process and loosening behavior under transverse loads of hi-lock nuts were simulated by finite element method（FEM）， and the simulated locking torque was verified by tightening tests. The simulation results show that within a certain range， the maximum radial displacement and the locking torque of the hi-lock nuts are linearly related to the extrusion amount approximately. With the extrusion amount increases， the maximum radial displacement and the locking torque both increase. The higher the locking torque of the hi-lock nuts， the better the anti-loosening performance. However， there is an optimal value of the extrusion amount for the anti-loosening performance. Once the extrusion amount exceeds the optimum value， increasing the amount of extrusion does not have a significant effect on the improvement of the anti-loosening performance.

Key words： hi-lock nut; extrusion; locking torque; anti-loosening performance

0 引言

高锁螺母是由美国HI-SHEAR公司于20世纪50年代研发的一类不可重复使用型紧固件，通常与高锁螺栓配合使用，因其具有防松性能好、预紧力可控、装配效率高等优点在航空航天飞行器的装配中得到了广泛的应用［1-3］。我国在以往的航空航天产品研发中对于此类紧固件多采用进口件，但随着采购周期、成本等原因的限制，对此类紧固件进行自主研发的需求和必要性大大提高。目前国内已有一些完成国产化的高锁螺母系列，但材料、规格并不齐全［4］，对高锁螺母仍需要开展细致与系统的工作。

高锁螺母由工艺部分和工作部分组成，两部分之间由拧断槽连接。高锁螺母的工艺部分主要是在安装时起到扳拧的作用。在高锁螺母的装配过程中，通过对工艺部分施加扭矩，使其旋入螺栓中，直至与被夹紧件接触产生预紧力。随着预紧扭矩的不断增大达到拧断槽的设计拧断力矩时，工艺部分从拧断槽处断裂、脱落，连接处仅保留工作部分［5-6］。

高锁螺母的紧固性能体现在五个重要指标：锁紧力矩、拧断力矩、松脱力矩、预紧力和抗拉力［6］。其中锁紧力矩是指螺母旋入螺栓且未产生预紧力时所需的最大拧入力矩。锁紧力矩的产生主要是由于高锁螺母的螺纹连接部分使用了多点挤压收口工艺。在收口过程中内螺纹产生塑性变形，这样在与外螺纹配合时会产生过盈装配的效果，从而在装配过程中产生锁紧力矩，达到自锁防松的目的。

拧断力矩是高锁螺母拧断槽发生断裂时的拧紧力矩，由材料属性及拧断槽的结构形式和尺寸决定，而且拧断力矩是获得合适预紧力的主要因素。若拧断力矩过大，则最终产生的预紧力过大，导致螺纹及被夹紧件产生强度问题；若拧断力矩过小，则无法满足紧固要求。综合来看，锁紧力矩、拧断力矩及预紧力这三个参数之间还是密切联系的。其中预紧力是基本紧固目标，锁紧力矩对应防松要求，拧断力矩是装配控制的目标。预紧力与锁紧力矩的大小共同决定了拧断力矩的大小，三者之间存在扭拉关系。王立东等［7］对不同收口量下的钛合金自锁螺母进行了拧紧实验研究，结果表明在不同收口量下自锁螺母的安装力矩与预紧力基本成线性关系。吴南星等［8］分别对未收口以及收口后的高锁螺母进行了拧紧实验，验证了高锁螺母锁紧力矩是线性叠加到拧断力矩上的。

锁紧力矩是高锁螺母5个关键参数中最难设计与确定的。从锁紧力矩设计角度来说，需要高锁螺母的松动指标指导设计，使得锁紧力矩处于一个合适的区间内，既不过大导致安装不便甚至发生螺纹面磨损、涂层破坏等问题［9］，也不过小使其失去防松效果导致松动失效。锁紧力矩的影响因素众多，如材料参数、收口参数（收口点数、收口量等）、润滑参数等，而这些参数往往处于国外的技术封锁中，也是生产制造中的关键所在。

由于高锁螺母收口工艺的存在，内螺纹在经过收口挤压变形后的几何形状并不清楚，内外螺纹之间的接触面是复杂的三维曲面干涉配合，对其进行建模、仿真存在一定困难，相关有限元仿真工作较少，且不够细致［10］。目前针对高锁螺母的研究更多的是通过拧紧实验研究收口工艺与锁紧力矩之间的关系。吴南星等［11］通过拧紧试验研究了不同材料、润滑条件、表面处理方式对高锁螺母锁紧力矩的影响，拧紧实验结果表明高锁螺母的锁紧力矩会随着材料的硬度减小、润滑条件的改善而减小。孙景冬等［12］通过对不同收口因素下的自锁螺母进行试验发现，增大收口量、收口点数以及收口段壁厚可以增大锁紧力矩。

在对此类产品的设计及加工制造中，锁紧力矩等关键指标对最终的紧固性能起决定性作用。但是相关基础研究工作开展较少，尚不能开展相应的预测设计，导致产品研制成本高、周期长，大大影响了该产品的国产化进程。

本文针对UNJ螺纹高锁螺母的有限元建模方法开展研究，建立了有限元模型，对高锁螺母的收口及装配过程进行了有限元仿真研究，探究收口量对锁紧力矩的影响，并进行了实验验证。最后对不同收口量下的高锁螺母的防松性能进行了仿真研究。

1 有限元建模方法及软件开发

正如前文所述，高锁螺母经过挤压后，其内部变形不规则，无法直接建模，需先建立未收口的高锁螺母模型，再进行收口工艺仿真。

根据文献［13］提出的螺纹建模方法，首先建立螺母基体网格，再根据螺纹线方程计算螺纹部分网格节点位置，最后对螺母基体网格节点坐标进行修改，得到包含螺纹细节的网格模型。这种方法考虑了精准的螺旋形状，生成的网格均为六面体网格，网格规模和计算精度可控，提高了求解精度和求解效率。

本文分析对象为UNJ螺纹规格的高锁螺母，首先建立UNJ螺纹的螺纹线方程。UNJ螺纹是一种控制根部半径的英制螺纹，它的根部圆角比普通英制螺纹更大，其螺纹牙型尺寸如图1所示。其中P为螺纹的螺距，H为牙高，D为大径，D1为小径，D2为中径。

设螺纹面上任一点到轴向的距离为l，其轴向截面内角度为θ，牙根部的圆弧半径为r，如图2所示，半个螺距高度内的螺纹可以分为三段。

（1）0≤θ＜θ1對应螺纹牙顶段，其中

2 收口工艺过程仿真

利用前文介绍的建模方法及螺纹连接结构六面体网格生成软件建立不同网格密度的高锁螺母有限元仿真模型，对收口块施加螺母径向收口量，螺母底面约束轴向和转动自由度，如图5所示。铝合金高锁螺母材料参数见表1，其弹塑性参数通过材料拉伸试验测得，应力-应变关系如图6所示。

不同网格密度下收口后的轴截面螺纹高度方向路径上的径向位移ur结果如图7所示。图8所示为不同网格密度下径向位移量的相对误差。

从图7、图8中可以看出，在相同的收口量Δ作用下，不同网格密度的模型中最大径向变形结果随着网格密度的增大略有增大，当网格密度增大至周向60等分-螺距20等分时，再继续增加网格密度，最大径向位移相对误差不超过0.5%，考虑计算成本，计算可以采用周向60等分-螺距20等分的网格进行计算。

当收口块径向位移为0.2 mm时，螺母变形量最大，而当撤去收口块位移时，螺母会有轻微的回弹，径向变形量减小，最终形成四点收口的高锁螺母，不同时刻的应力分布云图见图9。

由图9可以看出，高锁螺母的安装工艺部分在卸载后残余应力相对较小，螺母的变形主要集中在与收口块接触的区域。考虑当高锁螺母拧紧结束后，其安装工艺部分会脱落，故建立仅含有螺纹部分的简化模型，省略工艺部分及拧断槽，如图10所示，并进行相同收口量的收口计算。

简化模型与原始模型收口后的径向变形结果如图11所示。可以看出，两种模型的径向变形量十分接近，原始模型的最大径向位移为-0.165 mm，简化模型的最大径向位移为-0.166 mm，二者仅相差0.001 mm。两种模型内螺纹沿着收口中心位置的轴截面上路径（图10中路径）分布，如图12所示。可以看出完整的高锁螺母模型由于受到安装工艺部分结构的约束，刚度更大，在靠近工艺部分的起始位置上的径向变形量相对简化模型的径向变形量会偏小，但考虑该位置的径向变形较小，对拧紧过程的锁紧力矩计算影响也很小，故后续计算都将采用简化模型。

在简化模型的基础上，改变收口量Δ的大小，分别取收口量为0.10 mm、0.11 mm、0.12 mm、0.13 mm、0.14 mm、0.15 mm进行收口工艺的仿真，得到收口工艺卸载结束后轴截面上沿高度方向路径上的径向位移分布如图13所示。不同收口量下收口挤压结束时刻与卸载结束时

刻的径向变形量如图14所示。由图13、图14可以看出，在挤压结束时刻内螺纹的径向变形量明显小于收口块上施加的收口量，而在卸载结束时刻，随着收口量的增大，径向变形量也不断增大。压缩最大时刻与卸载后的最大径向变形量和收口量之间均近似满足线性关系：

（Δe≈Δ－0.03；

Δr≈Δ－0.06）（9）

0.1≤Δ≤0.15

式中，Δe为压缩最大时的最大径向变形量；Δr为卸载后的最大径向变形量。

图15所示为卸载后高锁螺母的径向变形在螺母周向上的分布，可以看出，高锁螺母的径向变形主要集中在收口点位置对应的72°范围内。螺母上径向变形的周向分布是关于收口点位置对称的，且收口中心区域的变形最大，在收口点位置72°范围外的其他区域基本没有径向变形。

3 高锁螺母装配过程仿真

3.1 高锁螺母装配过程有限元模型

建立如图16所示的高锁螺母装配过程仿真模型，将收口工艺的计算结果导入，作为装配过程的初始条件。在螺母上表面施加转角θnut，保证拧紧结束时螺母已完全旋入。

3.2 不同收口量对锁紧力矩的影响

对不同收口量的高锁螺母进行装配仿真，得到不同收口量下的拧紧力矩曲线（图17），由图17可以看出，对于收口量较小的高锁螺母，在拧紧前期有明显的水平段，这是因为在螺母旋入的前期，螺母底部内螺纹首先旋入，这部分区域位于收口块的下端，其径向变形小于内外螺纹的配合间隙，故未产生锁紧力矩。随着螺母旋入角度的逐渐增大，内螺纹的径向变形逐渐增大。当内螺纹的径向变形量超过内外螺纹间配合间隙时，才开始产生过盈装配，逐渐产生锁紧力矩。

随着转角的增大，不同收口量下的拧紧力矩先是呈近似线性增大，这是由于随着螺母的旋入，螺母的收口部分逐渐与螺栓建立接触，过盈接触的部分越多，所需克服的力矩也就越大，当螺母旋入8π之后，拧紧力矩基本保持稳定，此时收口变形的内螺纹部分均与螺栓外螺纹建立接触，最终稳定力矩即为锁紧力矩。图18所示为不同收口量下的锁紧力矩，可以看出，在收口量为0.11～0.15 mm范围内，锁紧力矩随着收口量的增大而增大。

3.3 试验验证

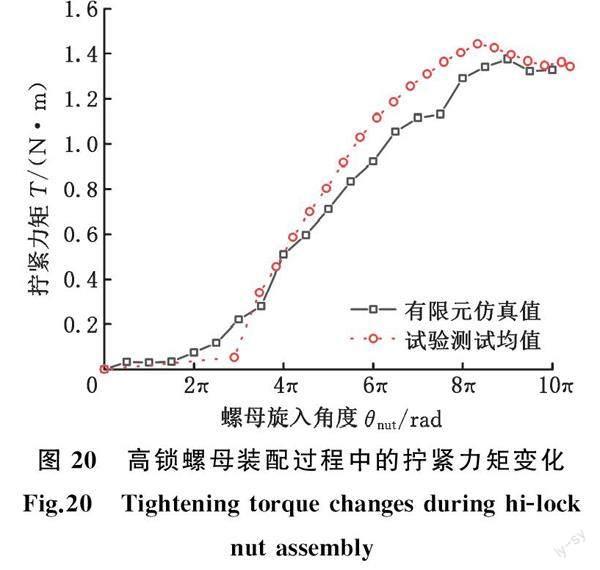
利用拧紧机对收口量为0.13 mm的高锁螺母进行拧紧装配试验，试验装置如图19所示。试验装置通过电机驱动，电机驱动的拧紧速度为4 r/min，利用扭矩传感器测得拧紧过程中拧紧力矩的变化，试验共重复5次，取均值。试验测试结果如图20所示。

由圖20可以看出，试验测得锁紧力矩与与仿真值趋势相同。随着高锁螺母的旋入，拧紧力矩逐渐增大，直到旋入8π后，拧紧力矩保持稳定。试验测得最终的拧紧力矩的稳定值即为锁紧力矩值。在拧紧试验中同时记录锁紧力矩与预紧力值，见表2。此规格高锁螺母拧断时预紧力均值为7.74 kN。

4 高锁螺母的松动过程仿真

在对螺纹连接结构进行松动分析时，往往采用图21所示的有限元模型［14］，模型由螺栓、螺母与被夹紧件组成。螺母端面与被夹紧件建立接触，内外螺纹间建立接触，约束螺栓头部自由度，对被夹紧件施加横向的振动载荷。

螺栓的预紧载荷控制为拧紧试验测得的均值7.74 kN。高锁螺母拧紧过程扭拉关系结果如图22所示。图22中也给出了由GB/T 16823.2—1997 中的理论公式计算出的理论上未收口的该规格高锁螺母的扭拉关系：

T=KFd（10）

式中，T为拧紧力矩；K为扭矩系数；F为夹紧力；d为公称直径。

由图22可以看出，高锁螺母收口后的扭拉关系也近似成线性关系。在相同夹紧力下，由于锁紧力矩的存在，收口后的扭矩要大于未收口时的扭矩。

在横向振动幅值为0.5 mm，振动频率为10 Hz的振动载荷下，不同收口量的高锁螺母的夹紧力衰退曲线见图23，可以看出，收口螺母在振动10个周期后的衰退量明显小于普通螺母的衰退量，收口量在一定范围内越大防松性能会越好，但当收口量达到0.13 mm后夹紧力衰退量基本保持一致，此时继续增大收口量对防松效果的提升较小。

5 结语

本文通过建立UNJ螺纹的螺纹线方程，对高锁螺母进行了有限元建模方法研究，并开发了高锁螺母的建模程序，得到了精细化的高锁螺母网格模型。对某规格高锁螺母的收口工艺过程、装配过程以及受到横向载荷时的松动过程进行了有限元仿真，讨论了收口量对高锁螺母锁紧力矩的影响，并对该高锁螺母在设计收口量下进行了拧紧试验，对其锁紧力矩进行了试验验证。通过有限元仿真主要得到以下结论：

（1）当收口量在一定范围内时，高锁螺母的收口量和螺纹最大径向变形量间满足线性关系。

（2）锁紧力矩与收口量在一定范围内近似满足线性关系，当收口量过小时，无法产生有效的锁紧力矩。

（3）高锁螺母收口量越大，其锁紧力矩越大，防松性能越好。对于该规格的高锁螺母，当收口量大于0.13 mm时，继续增大收口量对防松性能的提升不明显。

参考文献：

［1］赵庆云， 刘风雷， 刘华东. 世界先进航空紧固件进展［J］. 航空制造技术， 2009， 52（3）：54-56.

ZHAO Qingyun， LIU Fenglei， LIU Huadong. Development of Advanced Aerospace Fastener［J］. Aeronautical Manufacturing Technology，2009， 52（3）：54-56.

［2］LO J. The Next Generation Hi-lock and Hi-lite System［J］. SAE Technical Paper， 2017-01-2086.

［3］姜杰凤，董辉跃，柯映林.高锁螺栓干涉连接中极限干涉量［J］.机械工程学报，2013， 49（3）：145-152.

JIANG Jiefeng， DONG Huiyue， KE Yinglin. Maximum Interference Fit Size of  Hi-lock Bolted Joints［J］. Journal of Mechanical Engineering， 2013， 49（3）：145-152.

［4］徐梅香，胡建清，韩志忠.高锁螺栓、高锁螺母的国产化研制［J］.直升机技术，2009（3）：94-97.

XU Meixiang， HU Jianqing， HAN Zhizhong. Research and Manufacture of Civil Hi-lock Pins and Nuts［J］. Helicopter Technique，2009（3）：94-97.

［5］苗生沛， 张辉， 隋明丽.高锁螺母力矩及预紧力测试技术研究［J］.航空标准化与质量， 2021（3）：20-23.

MIAO Shengpei， ZHANG Hui， SUI Mingli. Research on Torque and Preload Test Method International Standard of Threaded Collar［J］. Aeronautic Standardization & Quality， 2021（3）：20-23.

［6］李英亮. 紧固件概论［M］. 北京：国防工业出版社， 2014.

LI Yingliang. Fasteners Basics［M］. Beijing：National Defense Industry Press， 2014.

［7］王立东， 刘风雷， 赵庆云. 收口量对钛合金自锁螺母锁紧性能的影响［J］. 航空制造技术， 2017， 60（23/24）：79-82.

WANG Lidong， LIU Fenglei， ZHAO Qingyun. Influence of Crimping Dimension on Locking Properties of Titanium Alloy Self-locking Nut［J］. Aeronautical Manufacturing Technology， 2017， 60（23/24）：79-82.

［8］吴南星，成飞，廖达海，等.高锁螺栓连接力学参数关系的实验研究［J］.机床与液压， 2017， 45（1）：77-80.

WU Nanxing， CHENG Fei， LIAO Dahai， et al.Experimental Study on the Relationship between the Mechanical Parameters of Hi-lock Bolt Connection［J］. Machine Tool & Hydraulics， 2017， 45（1）：77-80.

［9］劉仁志， 吴海荣， 王华明. TC16 钛合金六角自锁螺母加工技术研究［J］. 飞机设计， 2011， 31（3）：51-54.

LIU Renzhi， WU Hairong， WANG Huaming. TheApplication of TC16 Titanium Self-lock Hex Nut Critical Technologies［J］. Aircraft Design， 2011， 31（3）：51-54.

［10］张晓斌， 杨乾， 王洪飞， 等. 盲孔镶嵌自锁螺母锁紧力矩仿真及试验研究［J］. 现代制造工程， 2022， 497（2）：10-15.

ZHANG Xiaobin， YANG Qian， WANG Hongfei， et al. Simulation and Experiment on the Locking Torque of Blind Hole Enchase Self-locking Nuts［J］. Modern Manufacturing Engineering， 2022， 497（2）：10-15.

［11］吴南星， 鲍星， 徐梅香. 不同因素对高锁螺母锁紧力矩影响的研究［J］. 航空制造技术， 2016， 59（9）：103-106.

WU Nanxing， BAO Xing， XU Meixiang. Influence of Some Different Factors on Locking Torque of Hi-lock Nut［J］. Aeronautical Manufacturing Technology， 2016， 59（9）：103-106.

［12］孙景冬， 郑冬梅. 多种收口因素对GH738自锁螺母力矩衰减速度的影响研究［J］. 航空制造技术， 2020， 63（12）：87-91.

SUN Jingdong， ZHENG Dongmei. Various Influence on Locking Torque Descent Rate of GH738 Self-locking Nut［J］. Aeronautical Manufacturing Technology， 2020，63（12）：87-91.

［13］侯世远.螺纹联接松动机理研究［D］. 北京：北京理工大学， 2015.

HOU Shiyuan. Study on Mechanism of Loosening of Threaded Connection［D］. Beijing： Beijing Institute of Technology， 2015.

［14］王桢.螺栓连接结构抗松动性能评价指标研究［D］. 北京：北京理工大学， 2021.

WANG Zhen. Research on Evaluation Index of Anti-looseness Performance of Bolted Joints［D］. Beijing ：Beijing Institute of Technology， 2021.

（编辑 王艳丽）

作者简介：

张京东，男，1995年生，博士研究生。研究方向为螺纹连接结构松动机理及防松方法。E-mail：zhangjd@bit.edu.cn。

廖日东（通信作者），男，1972年生，教授、博士研究生导师。研究方向为动力机械结构强度与振动、结构密封与防松。E-mail：liaord@bit.edu.cn。

收稿日期：2022-08-02

基金项目：国家自然科学基金重点项目（U2141217）