运动解耦且正解符号化的8R两平移空间并联机构的设计与性能分析

杜中秋　沈惠平　孟庆梅　李涛　杨廷力

摘要：提出了机构1、机构2两个新型8R两平移空间并联机构，并对两个并联机构自由度进行了分析计算；推导出了两个机构的符号式位置正解和反解，并基于符号正解对两个机构的工作空间进行了分析；对这两个机构分别进行了刚度建模与动力学建模，分析了两个机构的刚度性能，并求得相同负载下两个机构的驱动力矩；最后对两个机构进行运动学、刚度和动力学性能对比，结果表明机构2为优选机型。

关键词：并联机构；方位特征方程；运动学；刚度；逆动力学

中图分类号：TH112

DOI：10.3969/j.issn.1004-132X.2023.12.005

Design and Performance Analysis of 8R Two-translational Spatial ParallelMechanism with Motion Decoupling and Symbolic Positive Solutions

DU Zhongqiu SHEN Huiping MENG Qingmei LI Tao YANG Tingli

Abstract： Two new 8R two-translational（2T） spatial PMs（PM 1 and PM 2） were proposed， and their degree of freedoms（DOF） were analyzed and calculated. The forward and inverse solutions of the symbolic positions of the two PMs were derived， and the workspace of the two PMs was analyzed based on the symbolic forward solution. The stiffness and dynamics of the two PMs were modeled respectively， the stiffness performance of the two PMs was analyzed， and the driving torque of the two PMs under the same load was obtained. Finally， the kinematics， stiffness and dynamic properties of the two PMs were compared， which shows that PM 2 is the preferred model.

Key words： parallel mechanism（PM）; position and orientation characteristic equation; kinematics; stiffness; inverse dynamics

0 引言

2～4自由度并聯机构因具有构件少、制造容易、控制相对简单等特点，在工业生产领域应用广泛［1-3］。目前对两自由度（2-DOF）平动并联机构的研究相对较少。两自由度平动并联机构可分为三类。

第一类为2-DOF平面五杆机构。该类机构仅当以两连杆的铰接点为末端执行器时能实现两维独立平移运动（2T）。一些学者对5R全铰链并联机构进行了运动学、奇异性和工作空间分析［4-6］，此类机构运动不解耦。

第二类为2-DOF两维平移的平面并联机构。该类机构常含有由若干个4个转动副（R）组成的平行四边形机构（简称4R机构）。LIU等［7］提出了一种两条支链中均包含1个4R平行四边形的机构，并将其作为一种基本模块应用于机床领域；HUANG等［8］对含有4R机构的全铰链两维平移机构进行了综合性能分析，并将其应用于电池质量检测设备中。一些学者也研究了滑块驱动且含有4R机构的两平移子链的并联机构的运动学、奇异性、工作空间和逆动力学［9-10］。这些二维平移平面并联机构运动也不解耦。

第三类为2-DOF二维平移的空间并联机构。 CHEN等［11］提出了运动解耦的RRR+PRRR机构；彭斌彬等［12］提出了两种具有较好侧向刚度的2-DOF平动并联机构，并分析了该机构的运动学性能；沈惠平等［13］提出了一种新型的4-DOF 3T1R并联机构，该机构所含的一条空间混合支链可演化出含1个4R机构的全铰10R两平移空间并联机构；SHEN等［14］设计了一种新型部分运动解耦的2P-5R两平移并联机构，并将其作为一条混合支链的主体，设计分析了一类3-DOF 2T1R机构。

沈惠平等［15］发明了两种仅由8转动副组成的两平移空间并联机构，该机构具有结构简单、制造容易和动力学性能好等优点，能够满足工业生产领域中作业范围较小、速度和精度较高的生产工艺需求。

1 机构的设计与拓扑特性分析

1.1 机构设计

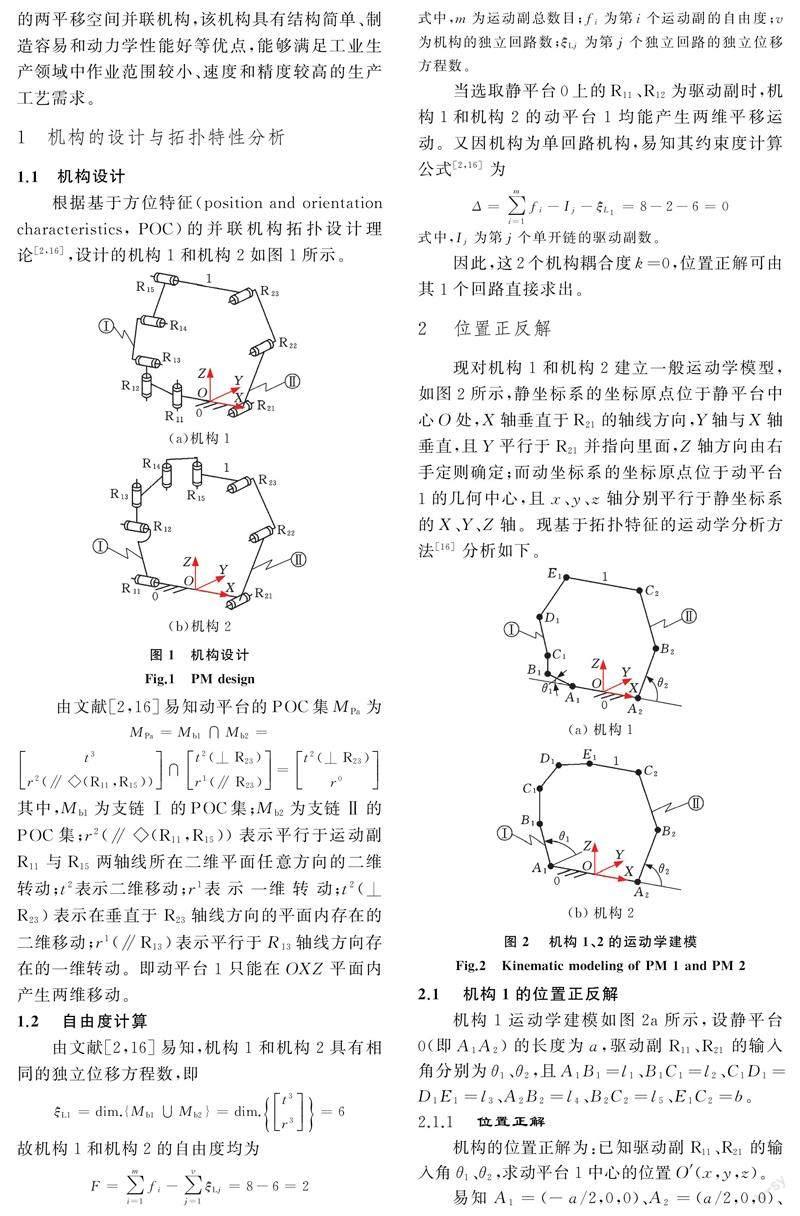
根据基于方位特征（position and orientation characteristics， POC）的并联机构拓扑设计理论［2，16］，设计的机构1和机构2如图1所示。

假设机构2和机构1具有相同的尺寸参数，即a=160 mm，b=150 mm，l1=100 mm，l2=80 mm，l3=120 mm，l4=130 mm，l5=190 mm。

同样对机构2建立三维CAD模型，从3D模型中测量得到两个驱动副R11、R21的初始输入角分别为θ1=0.2878 rad、θ2=－0.4569 rad，以及相对应O′点的输出值分别为x=214.57 mm、z=108.39 mm。

根据机构1的验证步骤，得到的各数值如表2所示。由表2可知，机构2的位置正反解的公式推导正确。

3 工作空间

本文采用基于符号式位置正解的极限搜索法［16］进行这两个2T并联机构工作空间分析。首先给定驱动副的输入角范围，然后利用符号式位置正解，通过MATLAB软件编程搜索所有动平台中心点，由这些点在三维空间组成的集合即为该机构能够达到的工作空间。

机构1和机构2的尺寸参数已分别在2.1.3节和2.2.3节给出。这里设定机构1和机构2的驱动副R11、R21输入角范围均为［－π，π］。通过MATLAB软件编程得到了两个2T并联机构的工作空间分别如图3a、图3b所示。由图3可知：

（1）因机构的输出运动为两维平移，所以它的工作空间为OXZ平面内的片状结构。

（2）机构1在Z方向具有较大的工作范围（－91.66 mm≤z≤320 mm），而机构2在X方向具有较大的工作范围（－315 mm≤x≤325 mm），其主要原因是机构1和机构2中的支链Ⅰ包含的3R子链轴线方向布置得不同，具体而言，机构1支链Ⅰ中的3R子链轴线方向平行于水平方向，因此，在Z轴方向提供了较大的活动范围，而机构2支链Ⅰ中的3R子链轴线则平行于竖直方向，因此，在X轴方向提供了较大的活动范围。

（3）机构1和机构2的工作空间具有较好的对称性，且机构1和机构2中间部分凹槽处完全对应；经分析，该处对应于θ2=arctan2z2x+b－a时机构满足的输入奇异。

4 刚度分析

本文采用基于虚拟弹簧法［18-20］的刚度分析方法对两个2T机构进行刚度分析。当机构的连杆弯曲变形很小且材料服从胡克定律时，连杆可视为悬臂梁，本文就是将其视作悬臂梁来分析其末端变形并求解其刚度矩阵Krodi［20］。

4.1 刚度基本原理

机构动平台在承受外力和力矩Fi后，因杆件变形和被动副变形会产生微小的变形量δt。用建立的6-DOF虚拟弹簧表示空间中三个方向的线性变形和扭转变形，由此建立微分表达式［20］如下：

4.4 机构1与机构2的刚度性能对比分析

根据4.2节和4.3节建模分析的刚度矩阵，可分别计算出机构动平台参考点O′在某一姿态下的整体静刚度矩阵K（6×6），其中，主对角线前3项为机构在X、Y、Z轴方向的扭转刚度（单位：N·m/rad），后3项为机构X、Y、Z轴方向的线性刚度（单位：N/m），但由于扭转刚度和线性刚度的量纲不一致，因此，对刚度矩阵中主对角线上的元素分别取均值进行分析，即扭转刚度η1=（K11+K22+K33）/3，线性刚度η2=（K44+K55+K66）/3［21］。

为了准确反映两机构因拓扑结构不同引起的刚度性能上的差别，设两机构对应的杆件长度和截面积参数不变，且选取两机构工作空间重叠部分进行刚度性能分析，得到两机构在10 mm≤x≤90 mm，85 mm≤z≤175 mm工作空间上的刚度变化趋势，如图7～图9所示。

综合图7～图9可得如下结论：

（1）在选定的工作空间范围内，机构2的支链Ⅰ的扭转刚度和线性刚度均优于机构1中支链Ⅰ的扭转刚度和线性刚度，且机构1和机构2中支链Ⅰ的扭转刚度变化平缓。

（2）由于两机构的支链Ⅱ具有相同的拓扑结构和尺寸参数，故其刚度变化趋势也完全相同。

（3）机构1和机构2中支链Ⅱ的扭转刚度和线性刚度均远大于支链Ⅰ的的扭转刚度和线性刚度，故图9中机构1和机构2整体的扭转刚度和线性刚度变化趋势和支链Ⅱ的扭转刚度和线性刚度变化趋势相似。

（4）机构2的扭转刚度大于机构1的扭转刚度，而线性刚度小于机构1的线性刚度。

5 动力学分析

本文根据基于虚功原理的序单开链法建立机构1和机构2的动力学模型，从而求得两机构驱动力矩的理论值，再通过ADAMS软件进行仿真，验证了理论模型的正确性。

5.1 机构1的动力学建模

5.1.1 机构1动平台的速度与加速度

雅可比矩阵［1，16］是输入关节速度到机构末端输出速度的映射，由于矩阵内部元素与位置有关，因此，在工作空间内部不同位置处，矩阵内部的元素大小也会产生变化，其映射关系为

式中，mij为杆件ij的质量；aijmid为杆件ij的质心加速度；ωij、εij分别为杆件ij的角速度与角加速度；OIij（ij指各杆件）为各杆件ij质心处的惯量矩阵，如OIAB指杆件AB质心处的惯量矩阵。

QE1C2为系统中各构件所受的外力与外力矩的矢量矩阵；

Jv、Jω分别为杆件的移动速度雅可比矩阵和角速度雅可比矩阵；δX、δθ分别为移动虚位移和转动虚位移；δq为广义虚位移。

将各杆速度、加速度值代入式（17）、式（18），即可求出驱动力矩TAiBi（i=1，2）。

设机构中各杆件的质量均为建模的默认值，分别为mA1B1=0.1003 kg，mB1C1=0.0595 kg，

mC1D1=mD1E1=0.1160 kg，mA2B2=0.1287 kg，mB2C2=0.1710 kg，動平台与负载的总质量mE1C2=9.5429 kg。将上述参数代入动力学方程（式（17）～式（19）），将5.1.1节的输入函数作为驱动副的输入，运用MATLAB计算（忽略摩擦）该机构的驱动力矩，结果如图11所示。

同时，将虚拟样机导入ADAMS中，选取运动仿真时间为5 s进行仿真，结果如图11所示。易知，驱动力的理论计算曲线与ADAMS仿真曲线基本一致，相对误差在0.02%以内，产生误差的主要原因在于，ADAMS软件仿真是基于Lagrange方程建立的动力学仿真模型，而本文主要采用基于虚功原理的序单开链法，在计算时存在舍入误差和累计误差，因此，可以认为本文动力学模型是正确的。

5.2 机构2的动力学建模

5.2.1 机构2动平台的速度与加速度

机构2动平台速度与加速度分析过程与机构1类似。

设定机构2与机构1具有相同的运动规律（区别在于初始角度不同），即θ1=π30t－35.83°·π180，θ2=π36t－79.65°π180。经过计算得到机构2动平台基点的理论速度与加速度如图12所示。

经仿真对比分析发现：机构2的理论速度和加速度分别与仿真值一致，故速度与加速度的理论计算是正确的，且X方向和Z方向的加速度变化值均较小，表明机构2动平台具有较好的稳定性。

5.2.2 机构2动力学模型的建立

同样，计算机构2各杆件的速度与加速度，并根据基于虚功原理的序单开链法对机构2建立动力学方程，利用MATLAB软件计算后得到机构2的驱动力矩如图13所示。

进一步，将机构2的虚拟样机导入ADMAS后进行仿真，得到图13所示的仿真力矩计算值。对比发现机构2的动力学建模也是正确的。

6 机构1与机构2的综合性能对比

6.1 运动学性能对比

6.1.1 位置正反解对比

由2.1节和2.2节位置分析可知，机构1和机构2均具有符号式位置正解，且具有部分解耦性，区别在于机构1在X方向上的位置仅由R11副的输入角θ1决定，因而具有解耦性，而机构2在Z方向上的位置仅由R11副的输入角θ1决定，因而具有解耦性。

6.1.2 工作空间对比

在X方向上，机构1的工作范围为－105 mm≤x≤95 mm，机构2的工作范围为－315 mm≤x≤325 mm，前者为后者的31.25%；在Z方向上，机构1的工作范围为－91.66 mm≤z≤320 mm，机构2的工作范围为－20 mm≤z≤180 mm，前者为后者的205.83%；机构1的工作空间面积为82 332 mm2，机构2的工作空间面积为128 000 mm2，前者为后者的64.32%。因此，机构1在Z方向具有较大的活动范围，而机构2在X方向具有较大的活动范围。从机构的整体工作面积分析可知，机构2具有较大的工作空间，可认为机构2为较优机型。

6.1.3 动平台速度对比

由图10a、图12a易知，在机构的驱动副运动速度相同的情况下，0～5 s两种机构的动平台速度为：①在X方向上，机构1动平台速度的平均值（25.3703 mm/s）大于机构2动平台速度的平均值（9.0858 mm/s），前者为后者的2.8倍，机构1动平台速度的最大值（45.4855 mm/s）远大于机构2动平台速度的最大值（10.7567 mm/s），前者为后者的4.2倍；②在Z方向上，机构1动平台速度的平均值（3.8464 mm/s）小于机构2动平台速度的平均值（7.9245 mm/s），前者为后者的48.54%，机构1动平台速度的最大值（5.4880 mm/s）小于机构2动平台速度的最大值（8.5712 mm/s），前者为后者的64.03%。

6.2 刚度性能对比

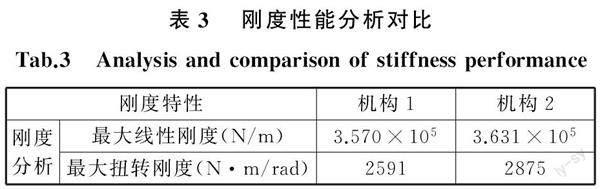
如4.4节所述，在10 mm≤x≤90 mm、85 mm≤z≤175 mm工作空间上，机构2的扭转刚度比机构1的扭转刚度约大9.88%；而机构2的线性刚度比机构1的线性刚度约小1.68%，具体分析对比如表3所示。

6.3 动力学性能对比

6.3.1 加速度对比

同样，在机构的驱动副运动速度相同的情况下，0～5 s内两种机构的动平台加速度为：①在X方向上，机构1动平台加速度的平均值（0.6742 mm/s2）略大于机构2的平均值（0.6243 mm/s2），前者为后者的107.99%，机构1动平台加速度的最大值（0.7390 mm/s2）略大于机构2的最大值（0.7313 mm/s2），前者为后者的101.05%，②在Z方向上，机构1动平台加速度的平均值（8.2150 mm/s2）远大于机构2的平均值（0.2983 mm/s2），前者為后者的27.5倍，且机构1动平台加速度的最大值（22.4079 mm/s2）远大于机构2动平台加速度的最大值（0.4458 mm/s2），前者为后者的50.3倍。因此，在速度与加速度方面，机构2的加速度较小，动平台运动更稳定，可认为机构2为较优机型。

6.3.2 驱动力矩对比

由图11、图13可知，在动平台1的运动轨迹相同且承受相同载荷的情况下：①机构1驱动副R11所需驱动力矩的平均值（-47.2245 N·mm）小于机构2驱动副R11所需驱动力矩的平均值（93.6097 N·mm），前者为后者的50.45%，且机构1中驱动副R11所需驱动力矩的最大值（-63.6388 N·mm）小于机构2所需驱动力矩的最大值（101.2488 N·mm），前者绝对值为后者绝对值的62.85%；②机构1驱动副R21所需驱动力矩的平均值（-187.1797 N·mm）远远大于机构2驱动副R21所需驱动力矩的平均值（-0.0596 N·mm），前者为后者的3140.6倍，且机构1中驱动副R21所需驱动力矩的最大值（-352.6265 N·mm）远远大于机构2的最大值（-0.2570 N·mm），前者绝对值为后者绝对值的1372.1倍。

从机构整体所需驱动力来看，机构2所需的驱动力矩相对较小，所需能量较小，且由图11、图13各驱动力矩变化幅度易知，机构2更平稳且误差较小，因此，认为机构2为优选机型。

7 结论

（1）根据基于方位特征（POC）的并联机构拓扑设计理论，设计了两种新型8铰链两平移空间并联机构，对这两个机构进行POC、自由度及耦合度等主要拓扑特征分析，结果表明两种机构均具有部分输入-输出解耦性，这对机构的轨迹规划和运动控制十分有利。

（2）根据拓扑特征运动学建模原理对这两种机构进行了运动学建模，得到了两种机构的符号式位置正反解，并进一步分析了它们的工作空间形状和大小。

（3）根据虚拟弹簧法对这两种机构进行了刚度分析，求得了它们在特定工作空间下的扭转/线性刚度分布图，并分析了它们的刚度特性。

（4）根据基于虚功原理的序单开链法建立了这两种机构的动力学模型，求得了它们的驱动力矩曲线，并验证了动力学模型的正确性。

（5）分析比较了两种机构的运动学性能、刚度性能和动力学性能，发现机构2运动平稳性更好、工作空间更大、刚度性能较优，且在负载相同的情况下所需驱动力矩更小，因此机构2为优选机型。

参考文献：

［1］梅莱J P.并联机器人［M］.黄远灿，译.北京：机械工业出版社，2016.

ML J P. Paralled Robots［M］. HUANG Yuancan， trans. Beijing：China Machine Press， 2016.

［2］杨廷力，刘安心，沈惠平，等.机器人机构拓扑结构设计［M］.北京：科学出版社，2012.

YANG Tingli， LIU Anxin， SHEN Huiping， et al. Theory and Application of Robot Mechanism Topo-logy［M］. Beijing：Science Press， 2012.

［3］刘辛军.并联机器人机构学基础［M］. 北京：高等教育出版社，2018．

LIU Xinjun. Fundamental of Parallel Robotic Mechanisms［M］. Beijing：Higher Education Press， 2018.

［4］GAO F， LIU X， GRUVER W A. Performance Evaluation of Two-degree-of-freedom Planar Parallel Robots［J］. Mechanism and Machine Theory，1997，33（6）：661-668.

［5］LIU X， WANG J， PRITSCHOW G. Kinematics， Singularity and Workspace of Planar 5R Symmetrical Parallel Mechanisms［J］. Mechanism and Machine Theory，2005，41（2）：145-169.

［6］LARA-MOLINA F A， KOROISHI E H， STEFFEN V， et al. Kinematic Performance of Planar 5R Symmetrical Parallel Mechanism Subjected to Clearances and Uncertainties［J］. Journal of the Brazilian Society of Mechanical Sciences and Engineering，2018，40（4）：1-15.

［7］LIU Xinjun， WANG Qiming， WANG Jinsong. Kinematics， Dynamics and Dimensional Synthesis of a Novel 2-DOF Translational Manipulator［J］. Journal of Intelligent and Robotic Systems，2004，41（4）：205-224.

［8］HUANG Tian， LI Zhanxian， LI Meng， et al. Conceptual Design and Dimensional Synthesis of a Novel 2-DOF Translational Parallel Robot for Pick-and-Place Operations［J］. Journal of Mechanical Design，2004，126（3）：449-455.

［9］沈惠平，吉昊，許正骁，等.三平移机构设计与运动学符号解及性能评价［J］.农业机械学报，2020，51（9）：397-407.

SHEN Huiping， JI Hao， XU Zhengxiao， et al. Design， Kinematic Symbolic Solution and Performance Evaluation of New Three Translation Mechanism［J］.Transactions of the Chinese Society for Agricultural Machinery， 2020，51（9）：397-407.

［10］沈惠平，顾晓阳，李菊，等.基于拓扑降耦的3T1R并联机构设计与运动学特性分析［J］.农业机械学报，2021，52（8）：406-415.

SHEN Huiping， GU Xiaoyang， LI Ju， et al. Topological Coupling-reducing Based Design of 3T1R Parallel Mechanism and Kinematics Performances Analysis［J］. Transactions of the Chinese Society for Agricultural Machinery， 2021，52（8）：406-415.

［11］CHEN C， ANGELES J. Generalized Transmission Index and Transmission Quality for Spatial Link-ages［J］. Mechanism and Machine Theory，2006，42（9）：1225-1237.

［12］彭斌彬，肖杰，陈小岗，等.新型2自由度并联平动机构构型及运动性能［J］.机械设计与研究，2010，26（1）：36-39.

PENG Binbin， XIAO Jie， CHEN Xiaogang， et al. Synthesis and Kinematics Performance of a Novel 2-DOF Parallel Translating Mechanism［J］. Mechanical Design and Research， 2010，26（1）：36-39.

［13］沈惠平，許正骁，许可，等.零耦合度且部分解耦的3T1R并联机构设计与运动分析［J］.农业机械学报，2019，50（4）：382-392.

SHEN Huiping， XU Zhengxiao， XU Ke， et al. Design and Kinematic Analysis of Zero Coupling and Partially Decoupled 3T1R Parallel Mechanism［J］.Transactions of the Chinese Society for Agricultural Machinery， 2019，50（4）：382-392.

［14］SHEN H P， TANG Y， WU G L，et al. Design and Analysis of a Class of Two-limb Non-parasitic 2T1R Parallel Mechanism with Decoupled Motion and Symbolic forward Position Solution-influence of Optimal Arrangement of Limbs onto the Kinematics， Dynamics and Stiffness［J］. Mechanism and Machine Theory，2022， 172：104815.

［15］沈惠平，杜中秋，孟庆梅.一种全铰链两支链两平移并联机构：CN115351771A［P］.2022-09-05.

SHEN Huiping， DU Zhongqiu， MENG Qingmei.A Full Hinge Two Branches and Two Translation Parallel Mechanism：CN115351771A［P］. 2022-09-05.

［16］沈惠平.机器人机构拓扑特征运动学［M］.北京：高等教育出版社， 2021.

SHEN Huiping. Topological Characteristics-based Kinematics for Robotic Mechanism［M］. Beijing：Higher Education Press， 2021.

［17］SHEN H P， ZHAO Y N， LI J， et al. A Novel Partially-decoupled Translational Parallel Manipulator with Symbolic Kinematics， Singularity Identification and Workspace Determination［J］. Mechanism and Machine Theory， 2021， 164：04388.

［18］WU G L， BAI S P， KEPLER J. MobilePlatform Center Shift in Spherical Parallel Manipulators with Flexible Limbs［J］. Mech. Mach. Theory，2014，75：12-26.

［19］WU G L， ZOU P. Stiffness Analysis and Comparison of a Biglide Parallel Grinder with Alternative Spatial Modular Parallelograms［J］. Robotica，2017，35（6）：1310-1326.

［20］WU G， SHEN H. Parallel PnP Robots—Parametric Modeling， Performance Evaluation and Design Optimization［M］. Singapore：Springer， 2020.

［21］孙驰宇，沈惠平，王一熙，等.零耦合度部分运动解耦三平移并联机构刚度建模与分析［J］.农业机械学报，2020，51（6）：385-395.

SUN Chiyu， SHEN Huiping， WANG Yixi， et al. Stiffness Analysis of Three-translation Parallelmechanism with Zero Coupling Degree and Partial Motion Decoupling［J］.Transactions of the Chinese Society for Agricultural Machinery， 2020，51（6）：385-395.

［22］杨廷力.机械系统基本理论：结构学·运动学·动力学［M］. 北京：机械工业出版社， 1996.

YANG Tingli. Basic Theory of Mechanical Systems：Structure·Kinematics·Dynamics［M］. Beijing：China Machine Press， 1996.

［23］沈惠平，肖思进，尤晶晶， 等.一平移两转动并联运动振动筛动力学建模与精度分析［J］.农业机械学报，2021，52（2）：394-400.

SHEN Huiping， XIAO Sijin， YOU Jingjing， et al. Dynamic Modeling and Precision Analysis of Parallel vibrating Screen with One-translation and Two Rotation［J］.Transactions of the Chinese Society for Agricultural Machinery， 2021，52（2）：394-400.

［24］黄凯伟，沈惠平，李菊， 等.一种具有部分运动解耦和符号式位置正解的空间2T1R并联机构拓扑设计与动力学建模［J］.中国机械工程，2022，33（2）：160-169.

HUANG Kaiwei， SHEN Huiping， LI Ju， et al. Topological Design and Dynamics Modeling of a Spatial 2T1R Parallel Mechanism with Partially Motion Decoupling and Symbolic Forward Kinematics［J］. China Mechanical Engineering， 2022，33（2）：160-169.

（编辑 王艳丽）

作者简介：

杜中秋，男，1996年生，硕士研究生。研究方向为机器人机构学。E-mail：duzq1028@163.com。

沈惠平（通信作者），男，1965年生，教授、博士研究生导师。研究方向为机器人机构学、并联机构及装备设计、一般机构学等。发表论文300余篇。E-mail：shp65@126.com。

收稿日期：2022-09-13

基金项目：国家自然科学基金（51975062）