基于NURBS曲线的超高速电梯导流罩多目标气动优化设计

陈西忍　叶文华　张朝宏　崔坤坤　冷晟　叶柳康

摘要：随着电梯梯速的提高，轿厢受到的气动阻力和升力越来越大，这不仅制约着梯速的进一步提高，也成为影响电梯舒适性和安全性的关键因素。为优化电梯的气动性能，利用NURBS曲线构建了包括导流罩、轿厢、对重和井道的电梯系统参数化模型。以气动阻力系数Cd和气动升力系数Cl为优化目标，利用敏感性分析筛选出对优化目标影响最大的4个关键设计参数。通过网格独立性检验选取合适的仿真计算网格，为缩短计算时间，结合最优空间填充设计的样本点建立Kriging模型对导流罩进行多目标优化，得到一系列Pareto解，并对优化前后导流罩的气动性能进行了对比分析。结果表明，降低导流罩侧面和后部凸凹度，增大导流罩总高和后部高，可以改善电梯系统的气动性能，优化后导流罩的Cd减小26.67%，Cl减小34.27%，并且在不同梯速下具有较好的适用性。

关键词：超高速电梯导流罩；NURBS曲线；最优空间填充设计；Kriging模型；多目标优化；气动性能

中图分类号：TU857

DOI：10.3969/j.issn.1004-132X.2023.12.006

NURBS Curve-based Multi-objective Aerodynamic Optimization Design forUltra-high-speed Elevator Fairings

CHEN Xiren YE Wenhua ZHANG Chaohong CUI Kunkun LENG Sheng YE Liukang

Abstract： With the increase of elevator speed， the aerodynamic drag and lift forces of the car became more and more great， which restricted the further improvement of elevator speed， and became the key factor affecting elevator comfort and safety. In order to optimize the aerodynamic performance of the elevators， a parameterized model of the elevator systems including fairing， car， counterweight and hoistway was built using NURBS curves. Taking aerodynamic drag coefficient Cd and aerodynamic lift coefficient Cl as optimization objectives， four key design parameters with the greatest impact on optimization objectives were selected by sensitivity analysis. In order to shorten the calculation time， a Kriging model was established to carry out multi-objective optimization of the fairings by checking the independence of the grid. A series of Pareto solutions were obtained. Finally， the aerodynamic performances of the fairings before and after optimization were compared and analyzed. The results show that the aerodynamic performances of elevator systems may be improved by reducing the convexity and concavity at the side and rear of the fairings and increasing the total height and rear height of the fairings. After optimization， Cd and Cl of the fairings are reduced by 26.67% and 34.27% respectively， and they have good applicability under different ladder speeds.

Key words： ultra-high-speed elevator fairing; non-uniform rational B-splines（NURBS） curve; optimal space-filling design; Kriging model; multi-objective optimization; aerodynamic performance

0 引言

隨着高层、超高层建筑的不断涌现，高速（梯速在2.5 ～6.0 m/s）和超高速（梯速大于6.0 m/s）电梯的应用日益广泛［1］。随着电梯梯速的增大，气动阻力占总阻力比例越来越高，气动升力也成为影响电梯舒适性和安全性的关键因素，这不仅制约了梯速的进一步提高，还增加了能耗［2-3］。而国内在高速和超高速电梯的研制上与国外相比相对落后，大部分技术被国外电梯生产商家所垄断。气动阻力和气动升力对超高速电梯运行时所消耗的能量以及振动、噪声和安全性都有很大的影响，因此，在设计一种新型超高速电梯时，气动阻力和气动升力是需要考虑的两个基本设计因素。

工程上常用的减阻和降噪的方法是优化高/超高速电梯轿厢的外形，并利用试验和数值模拟等方法对轿厢导流罩外形优化开展研究。BAI等［4］按比例搭建试验平台测试了四种不同形状轿厢在下落过程中的瞬时速度和轿厢前后的压力分布，得出了不同导流罩形状对轿厢压差阻力的影响。CAI等［5］利用锥曲线拟合设计了不同高度和约束参数的导流罩，利用FLUENT软件分析了阻力系数并选出了最优导流罩外形。李晓东等［6］利用计算流体动力学（computational fluid dynamics， CFD）方法对比分析了不同类型导流罩在运行过程中的气动性能，并初步确立了合适的导流罩外形。

采用动力学模型试验、实梯试验等传统方法获取导流罩外形参数与气动性能的关系，进行导流罩外形设计，不仅设计周期长，而且试验成本高，但是设计参数与优化目标之间的关系只能从这些计算结果中得出，因此，近年来有学者采用将CFD技术与优化算法相结合的方法对复杂外形进行优化设计。

曾天［7］利用多目标优化算法对椭球圆柱形导流罩的长轴和短轴进行优化，验证了模型的精度和优化结果的准确性。ZHANG等［8］基于非支配排序遗传算法Ⅱ和Kriging模型对列车头部外形进行了多目标气动优化设计。ZHANG等［9］采用椭圆曲线法建立了轿厢顶部圆弧的参数化模型，结合径向基函数代理模型对弧形进行优化，有效降低了电梯气动载荷。

然而，现有文献中对导流罩外形进行优化大多采用的是优选的方法对特定外形进行优化，而且优化过程中没有考虑对重的影响，很少有学者结合近似模型和优化算法对超高速电梯（ultra-high-speed elevator， UHSE）导流罩进行多目标优化，也没有为构建近似模型选出合适的实验设计（design of experiment， DOE）方法。随着梯速的提高，轿厢与对重交错压力波和涡流等空气动力学问题之间的相互影响加剧，传统的优化方法已无法满足行业发展的需求，难以综合考虑各种气动性能参数之间的相互影响。

综上所述，本文以某公司在研的单井道超高速电梯为例，利用NURBS曲线构建导流罩部分的参数化模型，以电梯系统的气动阻力系数和气动升力系数为优化目标，结合最优空间填充（optimal space-filing， OSF）设计和Kriging模型构建超高速电梯导流罩多目标优化模型。为了降低CFD计算成本，提高优化效率，利用敏感性分析从多个设计参数中提取出关键设计参数，对超高速电梯导流罩进行多目标自动寻优设计，验证构建的Kriging模型的精度，并对优化前后超高速电梯导流罩的气动性能进行分析。

1 多目标优化问题描述及流程

1.1 多目标优化问题描述

电梯的气动特性参数主要包括气动阻力、气动升力、气动噪声和克服气动阻力的能耗等，其中气动阻力与气动升力反映了电梯运行时的整体气动特性，直接影响到电梯的动力、稳定性、噪声和能耗等，在工程上常用气动力系数来描述气动力，其中气动阻力系数Cd和气动升力系数Cl的定义分别为

式中，X为用于定义几何外形的设计参数；xLi、xUi分别为设计参数的下限和上限；Gj（X）≤0为满足GB/T 7588—2020《电梯制造与安装安全规范》中运动部件距离关系要求的J个不等式约束条件；Hp（X）=0为满足井道尺寸、轿厢和对重在井道中位置等要求的P个等式约束条件。

1.2 优化设计流程

图1所示为超高速电梯导流罩优化设计流程，具体步骤如下：

（1）在CAD中建立电梯系统的几何模型，利用方程式使模型参数化，通过CAD与ANSYS Workbench之间的数据交换接口将两者模型尺寸相互关联，建立电梯系统的参数化模型；

（2）在Mesh和FLUENT模块中对参数化后的电梯系统进行模型处理、网格划分、数值模拟计算和网格无关性验证；

（3）在Parameter中对优化设计参数和目标函数值进行敏感性分析，提取出对目标函数值影响最大的关键设计参数，利用OSF设计实验样本点构建Kiging近似模型；

（4）采用多目标遗传算法对Kiging模型进行优化，得出Pareto最优解集，根据选出的验证点计算结果的拟合精度，并将优化前后电梯系统的气动性能进行对比分析，验证优化的精度与优化结果。

2 计算模型

2.1 数值模型

以载重量为1000 kg、速度为15 m/s的单井道超高速电梯为例，保留导流罩、轿厢、对重等主要结构，建立电梯系统的数值模型。其中，轿厢的尺寸（长×宽×高）为1.664 m×1.525 m×3.23 m，对重的尺寸（长×宽×高）为1.58 m×0.325 m×3.16 m。轿厢总高度（包括导流罩）为5.43 m，计算区域（井道）总长度也为5.43 m，轿厢宽度和深度均为2.6 m，轿厢距井道壁与轿厢距对重均为0.195 m。采用大地参考坐标系，坐标原点位于轿厢中心，其中Z轴沿着井道垂向，纵向和横向分别为X向和Y向，合理简化后的流场计算区域和边界设置如图2所示。计算区域边界条件设置如下：入口速度为15 m/s，出口压力为标准大气压；井道四周、轿厢与井道表面均为固定壁面，通过类似于风洞试验来模拟轿厢与对重交错时（最危险工况）的气动特性参数。

2.2 导流罩参数化设计

考虑到NURBS曲面可以对复杂的三维空间物体进行较好的描述［10］，且NURBS曲面在线性变换下是几何不变的［8，11］，因此，本文基于非均匀有理B-spline理论生成NURBS曲线，再由封闭的NURBS曲线生成面，通过若干面对导流罩外形进行逼近，从而实现导流罩外形的實体建模，通过导流罩表面的控制点实现对导流罩外形的控制。

由于轿厢在井道中的位置是左右对称的，上下运行工况是相同的，所以设计的轿厢顶部和底部的导流罩也是相同的，并且导流罩外形左右对称，因此只需要对左半部（或右半部）导流罩进行建模。为便于介绍优化设计变量，对控制导流罩外形的5条NURBS曲线进行编号，分别为L1～L5，建立的导流罩1/2模型及控制线编号如图3a所示。因为由L4和L5控制的最大横截面需要与现有的轿厢相匹配，所以不需要对其进行优化。根据主要控制线L1～L3的形状变化特征，13个控制点的选取如图3b所示。通过适当的约束和主从关系设置，提取导流罩外形的13个设计变量如图3c所示。

导流罩外形各主要控制线的变形函数如下：

式中，u为速度矢量；φ为流场通量；S为源项；Γ为扩散系数。

2.3.2 网格无关性验证

采用Tetrahedrons网格对计算区域进行网格划分。由于研究重点是导流罩、轿厢和对重，所以对三者的周围设置了网格加密区域。为消除网格划分方式对气动载荷计算结果的影响，划分了四套不同尺寸的网格进行网格独立性检验，四套网格的计算结果如图4和表1所示。

从四套网格对比结果可以看出，后三套网格得到的Cd和Cl的变化均在2%以内，而且压差阻力与黏滞（摩擦）阻力的浮动也很小，所以认为后三套网格都满足计算要求，考虑到计算时间和CFD计算的效率，本文选用网格2的网格尺寸。网格2的网格总数为76.12万，设置如下：轿厢和对重表面最大网格尺寸为50 mm，导流罩表面最大网格尺寸为25 mm，空间体网格最大网格尺寸为125 mm，边界层网格第一层网格厚度为0.5 mm，增长率为1.2，层数为6，划分后的网格如图5所示。

2.4 参数敏感性分析

超高速电梯的运行环境非常复杂，各设计参数对Cd和Cl都有不同程度的影响，考虑到进行CFD计算的时间和资源等成本因素，将所有目标都考虑在内是无法承受的，为了尽量减少训练样本点的数量，需要进一步研究优化目标与设计参数之间的关系。

利用灵敏度分析得到的各設计参数对优化目标的贡献度柱状图见图6。由图6a可以看出，对Cd影响最大的4个设计参数为dy11、dy10、dz6和dx5；由图6b可以看出，对Cl影响最大的4个设计参数为dz9、dz11、dy10和dx3。其中，dx3、dz6和dz2与两个优化目标之间的相关性是相反的。考虑到设计参数过多会增加计算成本，最终确定了对Cd和Cl平均影响最大的4个关键设计参数为dz11、dy10、dz5和dx5。

在超高速电梯导流罩气动优化设计中，为了满足电梯国标设计和实际生产的要求，避免出现没有实用价值的解，对关键设计参数的取值范围进行约束，如表2所示。

3 实验设计及响应分析

3.1 近似模型

在工程优化设计问题中，由于近似模型方法能够显著提高工程优化的效率，所以在设计时应用较多。常用的近似模型有：响应面模型［16］（response surface model， RSM）、径向基函数（radial basis functions， RBF）模型［17］、人工神经网络（artificial neural network， ANN）模型［18］和Kriging模型［19］等。其中RSM模型比较适用于线性问题的近似，在应用于非线性问题时近似精度往往很差。RBF模型适用于线性和非线性问题，但是无法直观地给出设计参数对目标函数的影响程度。ANN模型所需要进行的试验次数过多，不适用于计算量较大并且样本数据较少的电梯系统模型的建立。Kriging模型通过对样本点数据进行插值的方式给出设计参数与优化目标之间的最优线性无偏估计，对非线性程度较高问题能展现出理想的拟合效果，在全局与局部都具有较高精度。于是采用Kriging模型构建超高速电梯导流罩关键设计参数与优化目标之间的近似模型，表达式如下［20］：

3.2 实验设计方法

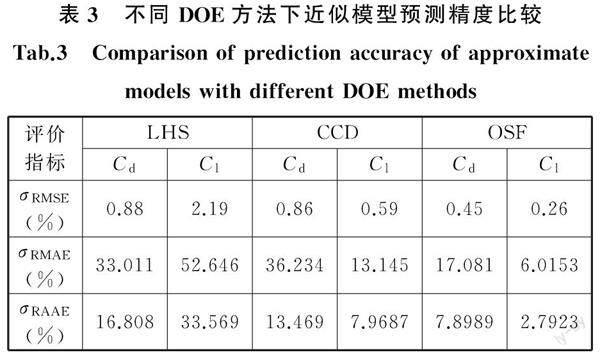
为了建立Kriging模型，首先要科学合理地设计实验样本，利用少量试验点得到较高精度的响应面。目前应用较广泛的DOE方法有拉丁超立方采样（Latin hypercube sampling， LHS）、中心组合设计（central composite design， CCD）和OSF设计。为了选择适合构建Kriging模型的实验设计方法，下文对比了上述3种DOE方法构建Kriging模型的近似精度，如表3所示。构建拟合的样本点由上述3种DOE方法设计4个关键设计参数得到，关键参数的取值范围如表2所示。为保证有足够大的采样空间覆盖率，选取样本点共计100个，并通过随机生成的3个额外试验设计点对近似模型的预测精度和优化效果进行分析。由表3可以看出：用OSF设计实验构建的Kriging模型在两个优化目标（Cd和Cl）上的3种误差评价指标（σRMSE，σRMAE和σRAAE）都是最小的，CCD设计实验次之，用LHS构建的Kriging模型得到的3种误差评价指标值最大，说明用OSF设计实验构建出的Kriging模型平均预测精度最高，所以下文采用OSF实验设计方法构建Kriging模型来对超高速电梯导流罩进行多目标优化。

3.3 采样方法及样本点的选择

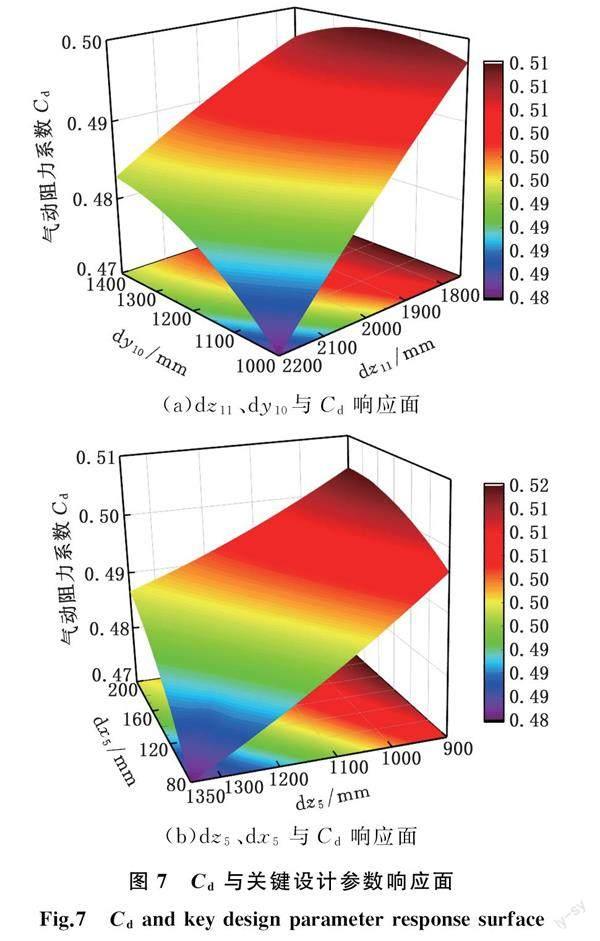
选用OSF［22］设计实验，初始试验设计样本点为28个，选取前25个作为训练样本点，剩余3个作为测试样本点，构造出的气动力系数与关键设计参数的Kriging近似模型如图7和图8所示。可以看出，优化目标Cd和Cl与关键设计参数之间并非是纯粹的线性关系。其中，Cd随着dy10、dx5的减小与dz11、dz5的增大呈现减小的趋势，Cl随着dy10、dx5的减小与dz11、dz5的增大呈现减小的趋势，这与图6的分析结果一致。

为验证建立代理模型的准确性，利用随机生成的3个额外试验设计点对模型精度进行分析，试验设计点及其各自响应值误差的分析结果如表4所示。可以看出，构建近似模型的预测值与仿真计算所得值的最大误差出现在Cl项上，误差为4.31%。综上可知，Kriging模型适用于构建超高速电梯导流罩多目标优化近似模型，精度满足要求。

4 多目标优化计算及结果分析

4.1 多目标遗传算法的实现

采用具有全局搜索能力能同时用于响应面优化系统以及直接优化系统的多目标遗传算法（multi-objective genetic algorithm， MOGA）［23-24］搜索关键设计参数在设计空间内的Pareto最优解，实现步骤如下：

（1）设计参数的编码和解码。考虑到以矩阵形式对4个关键设计参数进行求解难度较大，且不容易进行交叉操作，所以采用二进制编码来表示关键设计参数dx5、dz5、dy10、dz11。例如，dx5的定义域为［ai，bi］，要求的精度是小数点后j位，这就要求dx5的定义域至少要划分为（bi－ai）×10j个空间，则需要满足

（12）

解码过程是将编码过程逆转，即将dx5由二进制转为十进制，按下式计算：

（13）

式中，n为dx5所需要的二进制字符串长；decimal（si）表示dx5的字串si的十进制值。

（2）交叉、变异和选择操作。①交叉：考虑到超高速电梯导流罩多目标优化是典型的非线性最优化问题，所以采用在4个染色体中随机选择一个断点并交换断点右端部分的单点交叉；②变异：在求解此非线性最优化问题时采用反转变异法，变异总数为种群数与个体数的乘积，随机选中基因中的0、1进行交换；③选择：使用轮盘赌方法，将个体适应度按比例转换为轮盘的面积并旋转轮盘，选择球落点位置所对应的个体。

（3）多目标选择策略。尽管最小化Cd和Cl是超高速电梯导流罩优化的多目标选择策略，但这两个优化目标却有不同的优先级，考虑到气动阻力对气动性能的影响较大，即必须保证Cd小于临界值0.67的情况下，两个指标均尽可能的小。

（4）参数设置。用MOGA算法采用比例选择算子分别对Cd和Cl進行单目标优化求解［25］，经过算法参数敏感性计算试验，结合仿真实验和文献［26］，选择的算法参数如下：交叉率0.98，变异率0.01，初始种群数100，最大迭代次数20，收敛稳定百分比100%，最大允许Pareto百分比70%，稳定收敛百分比2%。

4.2 优化点的选取

图9给出了优化过程中优化目标与部分关键设计参数的变化历程。经过优化算法在设计空间中的采样，各关键设计参数和优化目标都呈现收敛的趋势，优化后的Cd和Cl较原始模型都有所减小。

图10给出了优化目标在像空间中的收敛情况，可以看出：在设置的设计空间内，Cd和Cl的最优解跨度范围较小，表明Pareto解集中个体差异较小，对工程设计而言，可选择的空间也较小。选取优化外形时，偏向于Cd和Cl均衡的样本点，为了得到满意的最优解，从图10中选取了3个典型的Pareto最优解，原始模型和优化后的三个Pareto最优解对应的关键设计参数和优化目标值汇总于表5中。其中案例0表示优化前模型，案例1～案例3表示优化后得到的Pareto最优解对应的模型，可以看出：优化后变形最明显的为导流罩总高，其次为导流罩后部高度和侧面凸凹度，导流罩后部凸凹度变形量较小；Cd和Cl无法同时取到最小，优化后Cd最小的为案例3，较原始模型减小约27.70%，优化后Cl最小的为案例1，较原始模型减小约35.02%。由于优化后得到的3个模型的Cd和Cl相差不大，最大相差仅0.0056，考虑到超高速电梯运行的稳定性和安全性要求，选取Cd和Cl都较小的案例2作为超高速电梯导流罩气动优化的最终设计方案。

4.3 优化结果的对比

根据最优设计方案的设计参数建立超高速电梯气动特性分析模型并进行数值模拟计算。由图11可以看出，与优化前相比，优化后的电梯系统轿厢表面的最大和最小静压值都有所减小，轿厢表面承受低压和高压的有效面积也明显减小。如图12所示，优化后的电梯系统在流场中运行时，底部产生的涡流面积减小，数量也有所减少（图中虚线方框位置），轿厢下方的低压区域面积也明显减小。涡流变小意味着气动噪声变小，井道内气流的稳定性增加。轿厢承受低压和高压的有效面积明显减小，电梯系统受到的气动阻力也一起减小。如图13所示，有无导流罩对轿厢受到的黏滞阻力影响很小，但是加装导流罩可以明显降低压差阻力，减小轿厢受到的气动阻力。与优化前相比，加装导流罩后可以将轿厢受到的气动阻力减小161.2 N，减少电梯系统的能耗。

4.4 不同梯速下稳健性分析

如表6所示，为了验证优化后超高速电梯导流罩在不同梯速下的适用性，对优化前后的超高速电梯导流罩模型在梯速为20，25，30，35，40 m/s时的优化目标值进行计算，得到优化前后不同梯速下的优化目标值与相对于优化前的减小率。可以看出，优化后的超高速电梯导流罩在不同梯速下都具有较好的性能，电梯系统的基本气动性能较优化前都有所改善，证明了优化结果在不同梯速下具有较好的适用性。

5 结论

基于NURBS曲线对导流罩进行了参数化设计，采用最优空间填充（OSF）实验设计构建了Kriging模型，用灵敏度分析了各设计参数对优化目标的贡献度，并验证了模型预测精度，最后利用多目标遗传算法对超高速电梯导流罩进行了多目标优化设计，结果表明：

（1）相比于拉丁超立方采样和中心组合设计方法，采用OSF实验设计方法构建的Kriging模型平均预测精度更高。

（2）阻力系数和升力系数不能同时取到最小。在一定范围内，降低导流罩侧面和后部凸凹度，增加导流罩总高和后部高，可以改善超高速电梯系统的气动性能。优化后的超高速电梯导流罩向着头形更长更尖、横截面积更小的方向变化。

（3）与原始导流罩外形相比，优化后给出的Pareto最优解的阻力系数和升力系数均得到明显减小，其中阻力系数最多减小27.70%，升力系数最多减小35.02%，优化结果在不同梯速下具有较好的适用性。

参考文献：

［1］JING H， ZHANG Q， ZHANG R， et al. Aerodynamic Characteristics Analysis of Ultra-high-speed Elevator with Different Hoistway Structures［J］.International Journal of Structural Stability and Dynamics，2022， 22（2）：2250020.

［2］ABDULLINA L R， BARBASHOV N N， LEONOV I V. Analysis of Possibilities to Reduce Energy Consumption of Elevator Systems［C］∥Proceedings of the 4th International Conference on Industrial Engineering. Berlin：Springer， 2018：167-175.

［3］PARK Y， NA J， SUNG K H， et al. Numerical Study on the Effect of Elevator Movement on Pressure Difference between Vestibule and Living Room in High-rise Buildings［J］. Building Simulation， 2019， 12（2）：313-321.

［4］BAI H， SHEN G， SO A. Experimental-based Study of the Aerodynamics of Super-high-speed Elevators［J］. Building Services Engineering Research & Technology， 2005， 26（2）：129-143.

［5］CAI W， LING Z， TANG P， et al. Optimization Design on Dome Shape of High-speed Elevator［J］. Proceedings of the 4th International Conference on Mechatronics， Materials， Chemistry and Computer Engineering，2015， 39：2362-2365.

［6］李晓冬，王凯. 高速电梯气动特性研究与优化［J］. 哈尔滨工业大学学报，2009， 41（6）：82-86.

LI Xiaodong， WANG Kai. Research and Optimization of Pneumatic Characteristics of High-speed Elevators［J］. Journal of Harbin Institute of Technology， 2009，41（6）：82-86.

［7］曾天. 通井道高速电梯多运行工况气动特性优化设计及其应用研究［D］. 杭州：浙江大学， 2018.

ZENG Tian. Optimization Design and Application of Aerodynamic Characteristics of High-speed Elevators with Shaft Passage under Multiple Operating Conditions［D］. Hangzhou：Zhejiang University， 2018.

［8］ZHANG L， ZHANG J， LI T， et al. Multi-objective Aerodynamic Optimization Design of High-speed Train Head Shape［J］. Journal of Zhejiang University：Science A， 2017， 18（11）：841-854.

［9］ZHANG R， ZHANG H， YANG Z. Aerodynamic Shape Optimization Design of the Air Rectification Cover for Super High-speed Elevator［J］. International Journal of Structural Stability and Dynamics， 2022，23（1）：2350002.

［10］TILLER P.The NURBS Book［M］. Milan：Springer， 1997.

［11］王緒鹏. 高速电梯气动特性优化与乘运性能评价方法研究［D］. 杭州：浙江大学， 2019.

WANG Xupeng. Research on the Optimization of Aerodynamic Characteristics of High-speed Elevators and the Evaluation Method of Ride Performance［D］. Hangzhou：Zhejiang University， 2019.

［12］WANG M， FREUND J B， LELE S K. Computational Prediction of Flow-generated Sound［J］. Annual Review of Fluid Mechanics， 2006， 38（1）：483-512.

［13］JANG D S， JETLI R， ACHARYA S. Comparison of the Piso， Simpler， and Simplec Algorithms for the Treatment of the Pressure-velocity Coupling in Steady Flow Problems［J］. Numerical Heat Transfer，1986， 10（3）：209-228.

［14］LAUNDER B E， SPALDING D B. The Numerical Computation of Turbulent Flows［J］. Computer Methods in Applied Mechanics and Engineering， 1974， 3（2）：269-289.

［15］YINHANGA M， HANYANGA J， MEILINGB D， et al. Experimental Study on Vibration Characteristics of Fluid-solid Coupling Cantilever Thin Aluminum Plate［J］. Journal of Vibroengineering，2020， 22（5）：1022-1036.

［16］MYERS R H， MONTGOMERY D C. Response Surface Methodology：Process and Product Optimization Using Designed Experiments［M］. New York：Wiley， 1995.

［17］HARDY R L. Multiquadric Equations of Topography and Other Irregular Surfaces［J］. Journal of Geophysical Research， 1971， 76（8）：1905-1915.

［18］HAJELA P， BERKE L. Neural Networks in Structural Analysis and Design：an Overview［J］. Computing Systems in Engineering，1992， 3（1）：525-538.

［19］SACKS J， WELCH W J， MITCHELL T J， et al. Design and Analysis of Computer Experiments［J］. Statistical Science，1989， 4（4）：409-423.

［20］于梦阁，潘振宽，蒋荣超，等. 基于近似模型的高速列车头型多目标优化设计［J］. 机械工程学报， 2019， 55（24）：178-186.

YU Mengge， PAN Zhenkuan， JIANG Rongchao， et al. Multi-objective Optimization Design of High-speed Train Head Shape Based on Approximate Model［J］. Journal of Mechanical Engineering， 2019， 55（24）：178-186.

［21］高亮，邱浩波，肖蜜，等. 优化驱动的设计方法［M］. 北京：清华大學出版社， 2020.

GAO Liang， QIU Haobo， XIAO Mi， et al. Optimization-driven Design Methods［M］. Beijing：Tsinghua University Press， 2020.

［22］WANG X， TSUNG F， LI W， et al. Optimal Space-filling Design for Symmetrical Global Sensitivity Analysis of Complex Black-box Models［J］. Applied Mathematical Modelling，2021， 100：303-319.

［23］FONSECA C M， FLEMING P J. Genetic Algorithms for Multiobjective Optimization：Formulation， Discussion and Generalization［C］∥International Conference on Genetic Algorithms. San Mateo， 1993：7129189.

［24］MURATA T， ISHIBUCHI H. MOGA：Multi-objective Genetic Algorithms［C］∥Proceedings of IEEE International Conference on Evolutionary Computation.New York：IEEE， 1995：5248085.

［25］王炳刚，饶运清，邵新宇，等. 基于多目标遗传算法的混流加工/装配系统排序问题研究［J］. 中国机械工程， 2009， 20（12）：1434-1438.

WANG Bingang， RAO Yunqing， SHAO Xinyu， et al. A MOGA-based Algorithmfor Sequencing a Mixed-mdel Fabrication/ Assembly System［J］. China Mechanical Engineering，2009， 20（12）：1434-1438.

［26］玄光男，林林. 网络模型与多目标遗传算法［M］. 北京：清华大学出版社， 2017.

XUAN Guangnan， LIN Lin. Network Models and Multi-objective Genetic Algorithms［M］. Beijing： Tsinghua University Press， 2017.

（编辑 王艳丽）

作者简介：

陈西忍，男，1997年生，硕士研究生。研究方向为气动特性分析与气动结构优化。

叶文华（通信作者），男，1965年生，教授、博士研究生导师。研究方向为智能制造、数控装备技术、现代集成制造系统等。E-mail：whye@nuaa.edu.cn。

收稿日期：2022-08-01

基金项目：国家自然科学基金（51775277）；苏州市吴江区科技创新项目（CSJ-202107201647-00000）