分布驱动式纯电动汽车直接横摆力矩控制研究

连晋毅，王 坤，任艳强

（太原科技大学机械工程学院，山西 太原 030024）

1 引言

电动汽车具有洁净、高效、可持续发展等特点，在节能减排方面所展现出的巨大优势，受到越来越多的关注［1］。分布驱动式纯电动汽车取消了机械传动装置，结构简单，传动效率更加高效，各个车轮能够独立驱动控制，为动力学控制带来了新的实现方式［2］，能够实现直接横摆力矩控制。

目前转矩分配主要为优化分配与非优化分配。非优化分配是一种简单的分配方式，只需满足车辆动力性即可；优化分配则考虑车辆行驶过程中的各种约束条件，使控制效果达到最优。为保证分布驱动式纯电动汽车稳定行驶，充分发挥四轮独立可控的优势，需要更加主动的控制策略，许多学者对此进行了相关研究。文献［3］提出了一种基于全局优化动态规划的最优转矩分配策略；文献［4］设计分层控制器，通过产生附加横摆力矩和前轮转向角来提高车辆的横向稳定性；文献［5］提出基于BP神经网络PID算法的电动汽车轮内电机转矩分配控制策略；文献［6］提出基于最小能耗的电动汽车横摆稳定性灰色预测可拓控制策略。文献［7］对目标函数进行优化得到系统的阻尼系数与特征频率，进行转矩分配；文献［8］基于最小二乘法对目标函数进行优化得到最优车轮力矩；文献［9］基于模糊控制原理控制车辆的附加转角保证车辆行驶的稳定性，并制定了具有驾驶员的驾驶意图四轮驱动力矩分配规则。

以上研究针对汽车操纵稳定性，通过不同转矩分配模式来控制电机转矩和横摆力矩分配实现车辆稳定性。

采用起作用集算法进行转矩分配，考虑路面的附着情况，协调控制各个轮胎间的动力输出，确保汽车稳定行驶，通过仿真对控制策略进行分析和验证。

2 车辆动力学模型

2.1 七自由度整车模型

构建车辆纵向，侧向，横摆运动以及四个车轮的转动的七自由度模型，进行整车动力学分析，如图1所示。

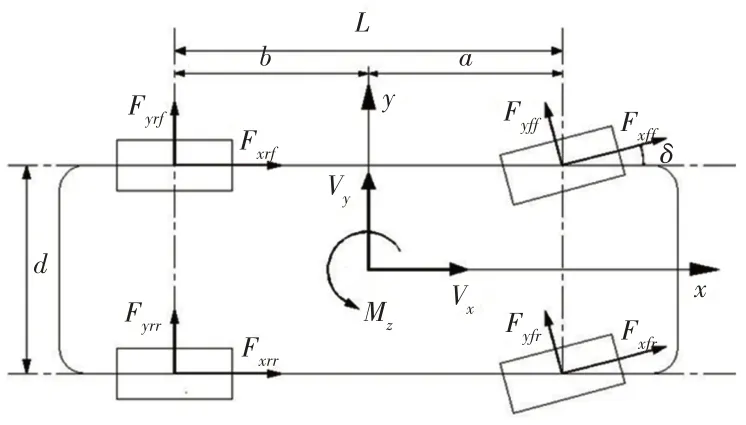
图1 七自由整车动力学模型Fig.1 The Vehicle Dynamics Model of Seven Free Degree

图中：O—质心；Vx—纵向速度；Vy—侧向速度；Fxi—车轮纵向力；Fyi—地面侧向力（i=fl，fr，rl，rr）；Mz—汽车绕Z轴的横摆力矩；L—轴距；a—质心到前轴距离；b—质心到后轴距离；d—汽车的轮距；δ—汽车的前轮转角。

动力学方程式，如式（1）～式（4）所示。

纵向运动：

侧向运动：

横摆运动：

车轮的转动：

式中：M—整车质量；ax—纵向加速度；ωy—横摆角速度；FX—汽车在质心处的纵向力；ay—侧向加速度；Fy—车身侧向力；IZ—z轴的转动惯量；Mz—转动力矩；ωi—各车轮的转动角速度；Tdi—车轮上驱动力矩；Tbi—车轮上制动力矩；Rw—车轮滚动半径；Iw—车轮转动惯量。

2.2 轮胎模型

“魔术公式”轮胎模型基于实验数据拟合轮胎各个物理量，拟合精度相对较高，使用简便［10］。其数学表达式为：

式中：y—侧向力或纵向力；x—轮胎侧偏角或纵向滑移率；B—刚度因子；C—形状因子；D—峰值因子；E—曲率因子。

忽略车轮的外倾角等影响，制动时轮胎的纵向力Fx0i为式（6），λi轮胎的纵向滑移率，ri为车轮的滚动半径，Wi为旋转角速度。

汽车转弯时，轮胎的纵向力Fy0i为：

以车辆左前轮为例，在Carsim中输出参数，并输出当前行驶工况下左轮胎的理想纵向力与侧偏力，汽车以80km/h速度双移线行驶，得到汽车左前轮纵向力和侧向力与实际行驶过程中对比，如图2、图3所示。

基于“魔术公式”轮胎模型估计所得轮胎力都能很好的跟随当前工况下Carsim 输出的理想值，CarSim 仿真输出的轮胎纵向力和侧向力随时间变化的趋势相同。

2.3 车体模型

在Simulink中对电机和控制器建模，用车体模型参数在Carsim中对车辆建模。车体模型参数，如表1所示。

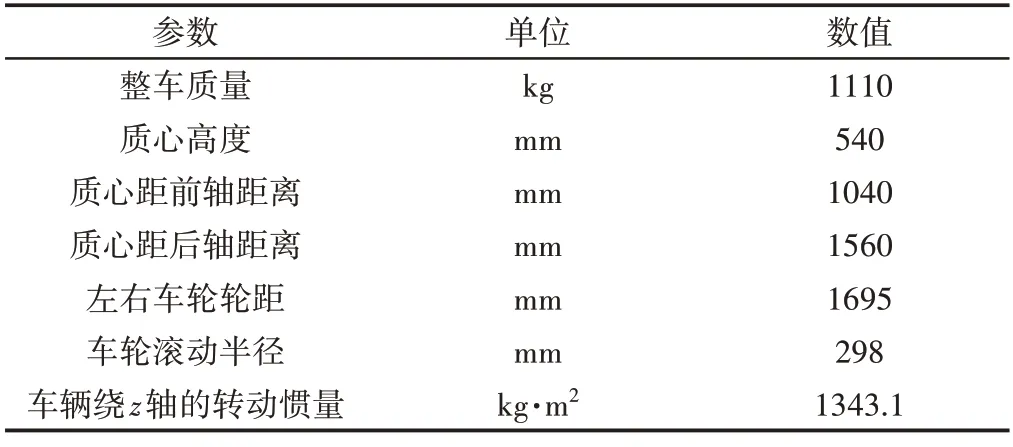
表1 车体模型参数表Tab.1 The Parameters of Vehicle Body

3 横摆力矩控制器设计

3.1 DYC控制研究

横摆角速度和质心侧偏角是评定汽车稳定性控制策略效果的重要参数［11］，两个参数共同决定汽车的稳定状态。这里所设计的控制器整体采用分层结构，上层为滑模变结构控制算法，根据汽车当前行驶工况下理想质心侧偏角、横摆角速度估计值与实际质心侧偏角、横摆角速度测量值二者之间的误差，决策出当前行驶工况下汽车稳定行驶所需的横摆力矩。下层控制器基于对车辆行驶状态的判断，采用起作用集优化算法对直接横摆力矩优化分配。控制器的具体结构，如图4所示。

图4 整车稳定控制器结构图Fig.4 The Structure of Vehicle Controller

3.2 理想参考模型

线性二自由度模型只考虑车辆的横摆和侧向运动，侧向运动及横摆运动的表达式为：

式中：kf，kr—前，后轮侧偏刚度，前后轮胎的侧偏角表达式为：

整理得到理想的横摆角速度为：

二自由度运动微分方程和理想的横摆角速度联立可得βd为：

上式所求βd与ωd只是理论意义的理想值，受路面附着系数影响，对于ωy。

其中，u为路面附着系数，联立式（13）中的三个公式可以得到式（14）。

实际行驶中，β很小，因此：

可知ωγd为：

综上，理想质心侧偏角为：

3.3 质心侧偏角观测器设计

质心侧偏角与横摆角速度的实际观测值可通过加权粒子滤波观测器实时观测。将式（1）～式（3）转为空间状态表达式（18）、式（19）。

式（18）为状态方程，X—状态变量；U—观测器输入，X=[Vx Vy ωγ]'；

U=[Fx Fy Mz]'；Wk—量测噪声；A—状态转移矩阵。式（19）为量测方程，Z为量测向量，Z=[Wfl Wfr Wrl Wrr]，Wi为车轮旋转角速度。利用基于粒子滤波算法的质心侧偏角观测器求解空间状态表达式，对质心侧偏角观测器的估计值进行加权融合处理。在Simulink中分别建立加权粒子滤波观测器与粒子滤波观测器，选择双移线仿真工况，路面附着系数为0.85，初始速度设为100km/h。仿真结果，如图5、图6所示。

图5 横摆角速度对比图Fig.5 The Comparison Map of Yaw Rate

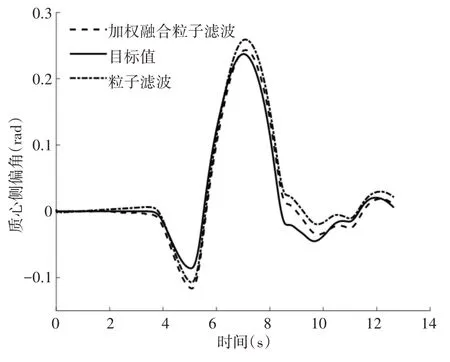
图6 质心侧偏角对比图Fig.6 The Comparison Map of Sideslip Angle

分析可知，粒子滤波算法与加权融合粒子滤波算法均能有效的跟随质心侧偏角与横摆角速度，加权融合粒子滤波算法的估计值更逼近状态变量目标值，观测效果更优。

3.4 滑模面和上层控制

滑模控制器的任务是计算出使车辆在理想状态下行驶所需要的附加横摆力矩。滑模变结构最大的不同在于它控制的相应系统的结构在不断变化，具有响应时间短，抗干扰能力强等特点，是车辆稳定性控制最常用的控制算法［13］。滑模面的选取为：

求导得：

选取指数趋近律为：

汽车的横摆运动，如式（23）所示。

面对不同的控制系统，滑动模态的设计方法也不同。系统存在抖振的现象不能彻底消除，只能将抖振削弱到一定的范围内［14］。针对抖振现象，采用边界层法，选取饱和函数改善切换面周围控制输入的平滑性，饱和函数为：

DYC 上层控制器以状态变量的误差作为输入，通过滑模变结构控制算法求得汽车在当前行驶工况下的附加横摆力矩ΔMz。附加横摆力矩ΔMz如式（25）。

在Matlab/Simulink中建立控制器仿真模型，如图7所示。

图7 滑模变结构控制器Fig.7 The Sliding Mode Variable Structure Controller

4 驱动力矩分配

4.1 转矩分配协调策略

分布驱动式纯电动汽车通过协调各轮之间的转矩，控制各个轮胎间的动力输出，确保汽车稳定行驶。下层控制器采用二次规划的最优分配算法，在引进多约束情况下，充分发挥各轮胎的作用。假设汽车左转时δ＜0，分析汽车的行驶状态，如表2所示。

表2 车辆状态分析表Tab.2 The Vehicle Status Analysis

4.2 基于起作用集算法的转矩分配

4.2.1 起作用集法

起作用集方法是求解二次规划最常见即有效的算法［15］，附加横摆力矩分配属于多约束范畴，可以将问题转化为二次规划。

系统只有不等式约束时，其数学模型为：

4.2.2 目标函数的确定

下层控制器以ΔMz为控制变量，四个轮胎为执行器。保证地面给轮胎的侧向力有一定的富余，提高车辆的行驶稳定性，以轮胎的纵向路面附着率为目标函数，合理分配各轮转矩，单个轮胎的附着利用率表达式为：

式中：u—路面附着系数。

以轮胎的路面附着力之和为目标函数，如式（28）所示。

式中：Ci—加权系数。

轮胎侧向力控制难度较大，忽略与纵向力之间的耦合，目标函数等效为：

式中：u，R—轮胎的滚动半径，转矩优化分配后的目标函数为：

4.2.3 约束条件

下层转矩分配器中，整车总纵向力约束条件为：

式中：Fq—车辆总的纵向力，将其等效为矩阵表达式为：

式中：Txi—轮胎转矩；Tq—期望的总转矩，Tq=FqR。

车辆在失稳状态下，需重新进行转矩分配。转矩分配之后四轮转矩和为Mq，Mq=Mz+ΔM，Mz为未施加转矩分配车辆绕Z轴的横摆力矩。将约束条件等效为力矩表达式：

四个车轮的纵向力满足路面附着条件的限制，约束条件为：

将其等效为力矩表达式为：

为满足轮毂电动的输出限制，这里永磁同步电机最大输出转矩为Tmmax，各个车轮最大驱动/制动力必须满足电机的输出外特性，约束条件为：

综上，附加横摆力矩的最优分配有两个等式约束，两个非等性约束，联立各个约束表达式，将其转化为矩阵表达式为：

得到二次规划函数后，利用起作用集方法求出目标函数的最优解。

5 仿真验证

在附着良好道路上以100km/h速度，在MATLAB/Simulink中验证双移线工况仿真结果的可靠性。分析图8可知，汽车在变道过程中从3.7s后出现甩尾状况，前轮转角不能按照标准正弦曲线连续输入，幅值与周期均发生了变化。分析图9可知，汽车向左换道时，右前轮R1与右后轮R2垂直载荷分别增加了1800N 和1700N多。未加控制前各轮胎的轮胎利用率，此种工况下的轮胎利用率极不均匀，特别是右前轮，路面附着利用率较大，此时驾驶员转动方向盘，车辆不能迅速做出准确响应，车辆处于危险工况，需重新优化分配，如图10所示。

图8 车轮转角输入Fig.8 The Wheel Angle Input

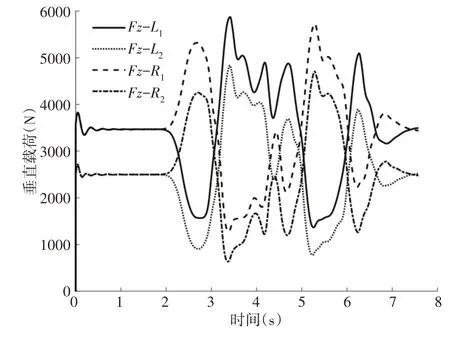
图9 轮胎垂直载荷Fig.9 The Tire Vertical Load

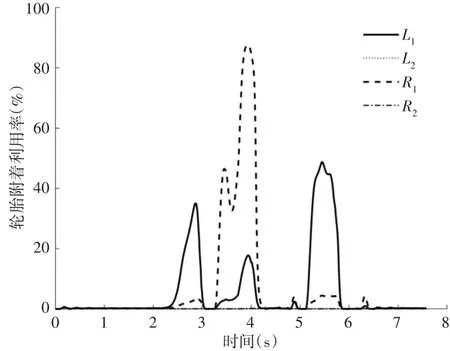
图10 未加控制制动轮胎利用率Fig.10 Uncontrolled Brake Tyre Utilization

下面采用起作用集法直接横摆力矩优化分配方式。图11中，传统液压制动下的车辆横摆角速度误差较大，而横摆力矩控制能够有效的跟随目标值。在图12 中，施加起作用集优化分配，β能够很好跟随目标值。液压制动时，β远高于理想值，车辆明显的发生侧偏现象。起作用集转矩优化分配后，车辆轮胎的附着利用率，如图13 所示。对比图10 可知，经过转矩的重新分配，左前轮的轮胎附着利用率提高，右前轮的轮胎附着利用率降低，地面能够给轮胎提供的纵向力以及侧向力仍有很大的裕度。起作用集转矩优化分配后的各个车轮转矩，如图14 所示。

图11 横摆角速度对比图Fig.11 Comparison of Yaw Angular Velocity

图12 质心侧偏角对比图Fig.12 Comparison of the Deviation Angle of the Center of Mass

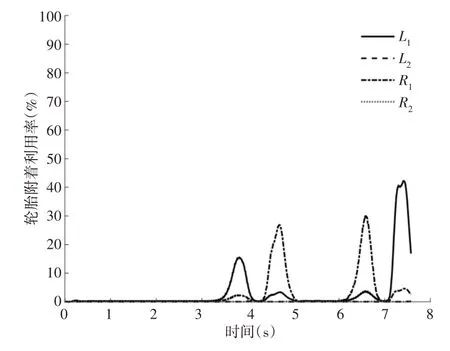
图13 起作用集优化分配轮胎利用率Fig.13 Optimal Allocation Tire Utilization in the Operating Set

图14 起作用集优化分配各轮转矩Fig.14 Operating Set Optimizes the Distribution of Each Wheel Torque

模拟低附着紧急转弯工况，车辆快速避开障碍物通常会紧急制动或者迅速转弯。设定汽车以80km/h 的恒速在附着系数为0.35的道路上先向左侧行驶一段时间后向右急转方向盘。车辆的侧向行驶理想路径与实际行驶路径，如图14所示。从图15可以看出，初始阶段汽车能够按照理想的路径向左按指定方向行驶，纵向距离在行驶到134m 附近时突然向右紧急转向，汽车偏离理想行驶路径，在纵向距离行驶至160m 左右时，期望路径为汽车回到初始路径保持稳定行驶，但实际车辆发生侧滑，汽车继续往右偏离行驶，直至纵向距离行驶至190m 附近时，汽车才开始回归初始行驶路径，在纵向距离行驶至208m 附近时，汽车恢复稳定。图16为车轮垂直载荷，以左前轮L1为例，在（0～1）s 左右，轮胎的垂直载荷迅速的升高至3700N，在（1.4～5.8）s 期间，汽车沿指定的方向恒速行驶，车轮的垂直载荷维持在一个固定值3500N 左右，在6s左右，汽车突然向右转动方向盘，汽车出现侧滑，轮胎的垂直载荷急剧的增加至6300N附近，7s 附近时，车辆开始回到初始行驶路径，轮胎的垂直载荷迅速的下降2100N 附近。车辆向右行驶时，地面将绝大部分的力施加于左前轮，左前轮没有多余的转矩储备处理不稳定工况，汽车发生侧偏现象。

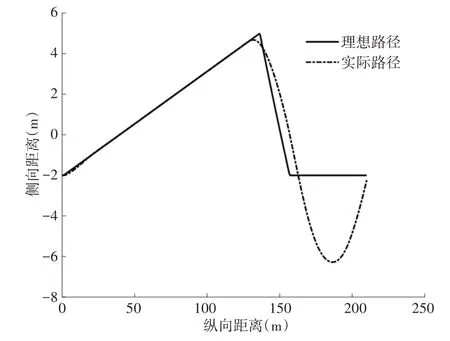
图15 车辆行驶路径Fig.15 The Vehicle Driving Path

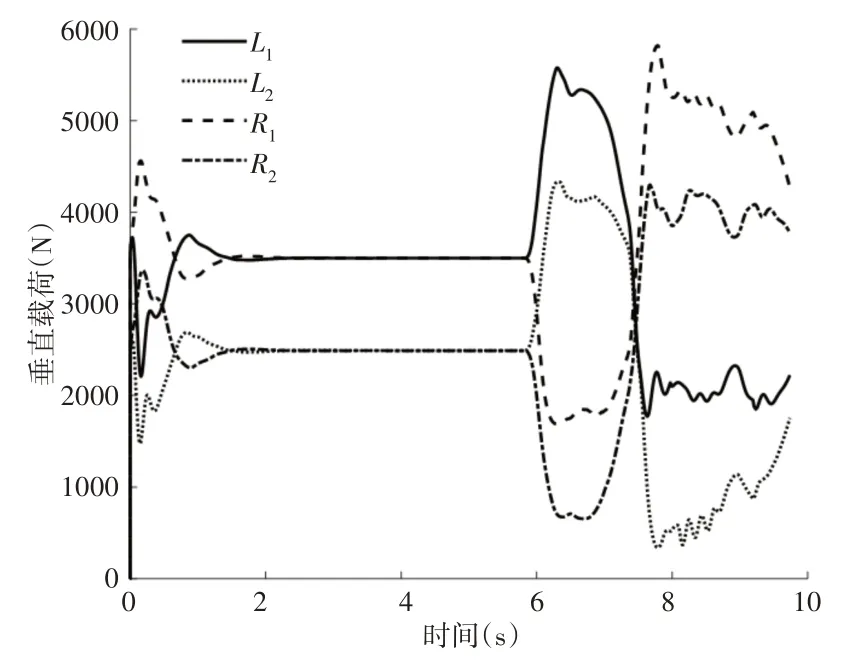
图16 车轮垂直载荷Fig.16 The Tire Vertical Load

横摆角速度对比图，如图17所示。分析低附着紧急转弯工况下的横摆角速度的理想曲线，当车辆直线行驶时，左右驱动轮转矩均不发生变化，车辆在6s附近紧急向右转动方向盘，然后迅速的向左行驶，最终趋于稳定状态。车辆在6.6s 时存在小幅度的右转工况，这是为了防止紧急转弯工况下突然转向，车头和车尾产生反向力导致车轮短暂抱死。横摆角速度均增大，车辆行驶时更加稳定，这说明横摆力矩控制的车辆很好的跟随理想的状态，不论左转还是右转，经过起作用集算法控制后的横摆角速度，接近于理想值，汽车行驶路径符合预期目标。

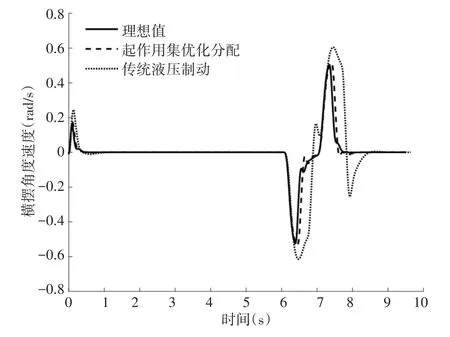
图17 横摆角速度对比图Fig.17 The Comparison Map of Yaw Rate

质心侧偏角的跟随值，基于起作用集法分配直接横摆力矩控制的车辆质心侧偏角能够跟随理想的质心侧偏角，如图18所示。车辆在第6s开始紧急向右转动方向盘，进行低附着紧急转弯工况时，不论左转还是右转，经过起作用集法控制后的质心侧偏角均减小，且最大值处响应时间滞后，对比传统液压制动的车辆，更接近理想值。路径跟随图，如图19所示。直接横摆力矩控制的车辆能够较理想的跟随目标车辆的行驶轨迹，虽然有侧滑现象，但幅度较小，车辆能够迅速的调整回归稳定状态。

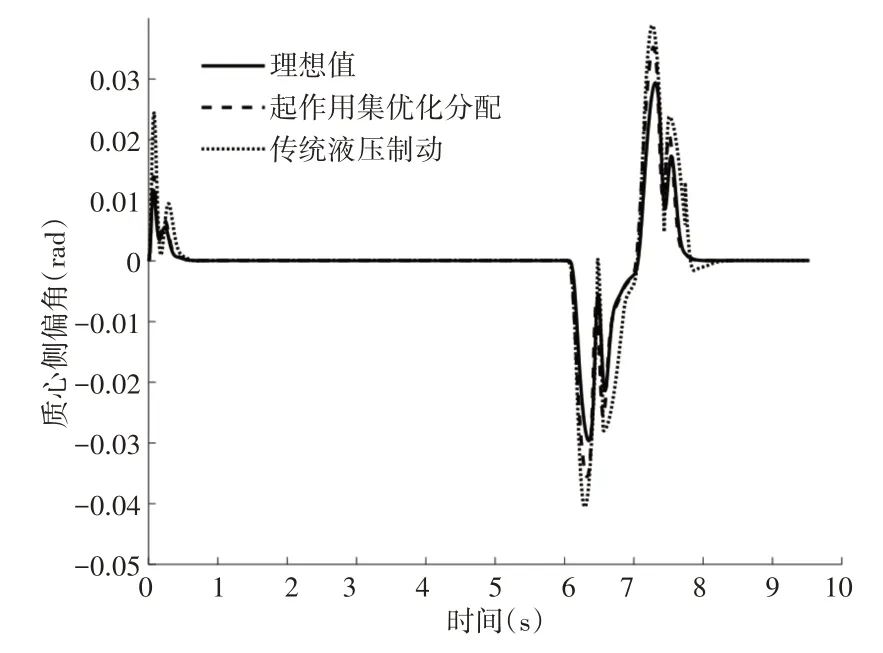
图18 质心侧偏角对比图Fig.18 The Comparison Map of Side Slip Angle

图19 路径跟随图Fig.19 The Path Following Diagram

6 结论

在分层控制的结构框架下，基于附加横摆力矩的转矩分配控制策略可改善分布式纯电动汽车的行驶稳定性。上层控制器决策出当前行驶工况下汽车稳定行驶所需的横摆力矩，下层控制器采用起作用集法对横摆力矩优化分配，基于附加横摆力矩进行转矩分配控制。通过双移线和低附着紧急转弯两种工况的仿真对比分析，发现所设计的直接横摆力矩控制策略，可明显改善分布驱动式纯电动汽车的操纵稳定性。