基于多岛遗传算法的燃料电池汽车模糊控制策略优化

王 恒，李 蒙，王 铁，赵 震

（太原理工大学车辆工程系，山西 太原 030024）

1 引言

汽车工业的迅猛发展在给人们带来便利的同时也加剧了能源危机与环境污染。在全球倡导节能减排的背景下，新能源汽车成为了世界各国关注的焦点［1］。燃料电池汽车（Fuel Cell Vehicle，FCV）作为新能源汽车的一种，具有比能量高、零排放、低噪声等优点，近来已为汽车行业研究的热点［2］。

FCV动力系统一般由燃料电池和动力电池共同组成，由于存在多个动力源，整车功率的分配问题显得尤为重要［3］。功率跟随型控制策略与模糊控制策略是FCV最常用的整车控制方式。文献［4］通过对单一燃料电池输出特性偏软，动态响应较差的研究，分别增加复合电源和动力电池作为辅助能源进行“削峰填谷”，提高燃料电池的耐久性，且复合电源相较于动力电池能够最大限度地回收制动能量，提高整车经济性。文献［5-6］将模糊控制策略和功率跟随型控制策略仿真结果进行对比，均表明模糊控制策略的整车经济性相较于功率跟随型控制策略有较大提高，且减少了燃料电池的起停次数，有利于提高其寿命。文献［7］对模糊控制策略进行改进，限制了燃料电池输出功率的变化率，对其寿命有了进一步的提高。然而功率跟随型控制策略不具有自适应性，模糊控制的隶属函数的制定也主要依靠工程与实践经验，所以二者还有较大的优化空间［8］。

这里以功率跟随型控制策略为基础，设计了FCV 模糊控制器，利用敏感性分析筛选设计变量建立了椭球基神经网络近似模型，以此模型为基础，采用多岛遗传算法对模糊控制的隶属函数进行优化，以提高整车经济性。

2 目标车型动力系统结构与建模

目标车型为某款中型燃料电池物流车，该车型包括燃料电池和动力电池两个动力源系统，其拓扑结构和整车参数，如图1、表1所示。燃料电池通过单向DC/DC转换器与动力电池间接并联，驱动电机与传动轴直接相连，具有结构简单、便于控制的特点［9］。基于此拓扑结构和整车参数，在MATLAB/SIMULINK中搭建了整车前向仿真模型。

表1 整车及动力系统参数Tab.1 Parameters of Vehicle and Powertrain

图1 燃料电池汽车动力系统拓扑结构Fig.1 Topology of Fuel Cell Vehicle Powertrain

3 模糊控制策略的设计

燃料电池汽车控制策略的制定需要满足以下原则［10］：

（1）燃料电池和动力电池须满足整车需求功率。

（2）保持动力电池荷电状态（State of Charge，SOC）处于设定范围，使动力电池始终处于浅充浅放的状态，延长动力电池寿命，并充分利用动力电池回收制动能量，降低氢耗。

（3）保证燃料电池的稳定运行，优化燃料电池工作点，使燃料电池尽可能工作在高效区间。

为了在满足功率需求的同时，使动力电池SOC保持稳定。选取整车需求功率Pload和动力电池SOC相对于目标值SOC*的变化量ΔSOC作为模糊控制器的两个输入变量，燃料电池系统输出功率Pf作为输出变量。Pload分为六个模糊子集｛NH、NM、NL、PL、PM、PN｝，含义为：负高、负中、负低、正低、正中、正高；ΔSOC分为五个模糊子集｛NB、NS、Z、PS、PB｝，含义为：负大、负小、零、正小、正大；Pf分为六个模糊子集｛L0、L1、L2、L3、L4、L5｝，含义为：关闭、小、较小、较大、大、最大。各变量的模糊分布及其三维曲面图，如图2所示。

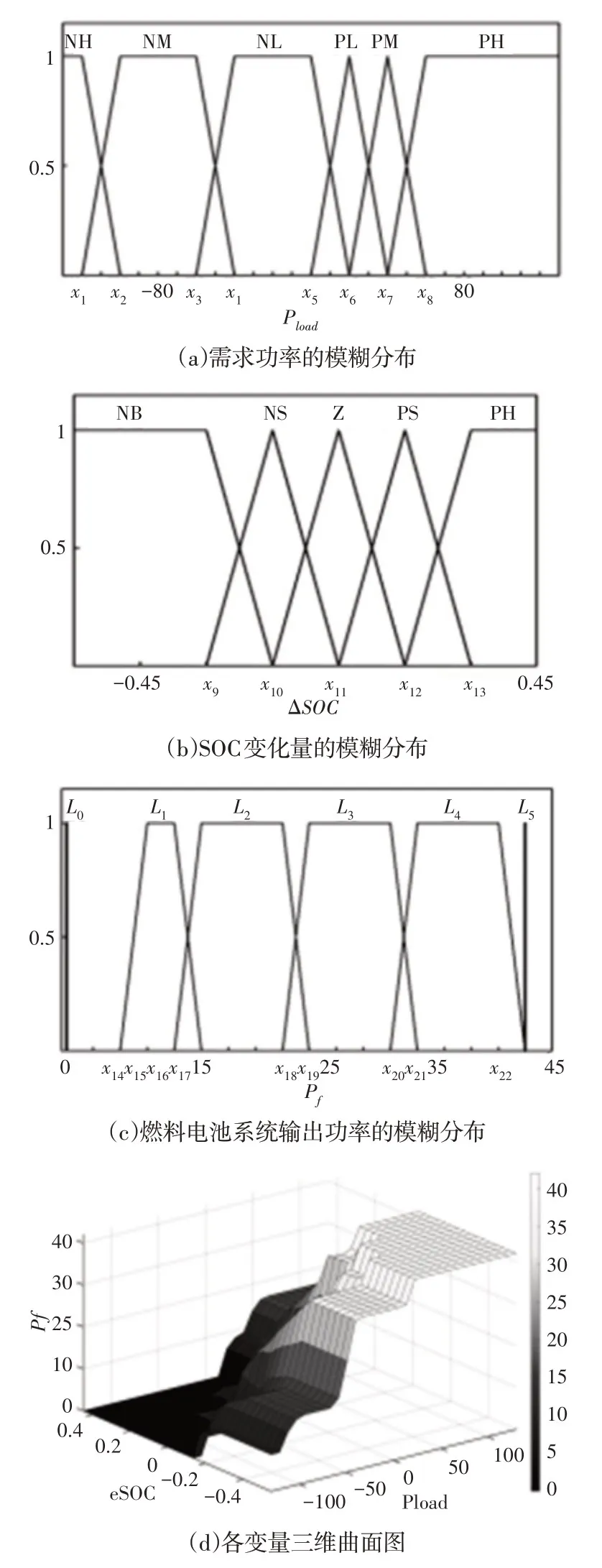
图2 各变量分布图Fig.2 Distribution Diagram of Each Variable

根据功率跟随型控制策略控制逻辑、燃料电池汽车控制原则以及实际工程经验制定模糊控制规则，如表2所示。

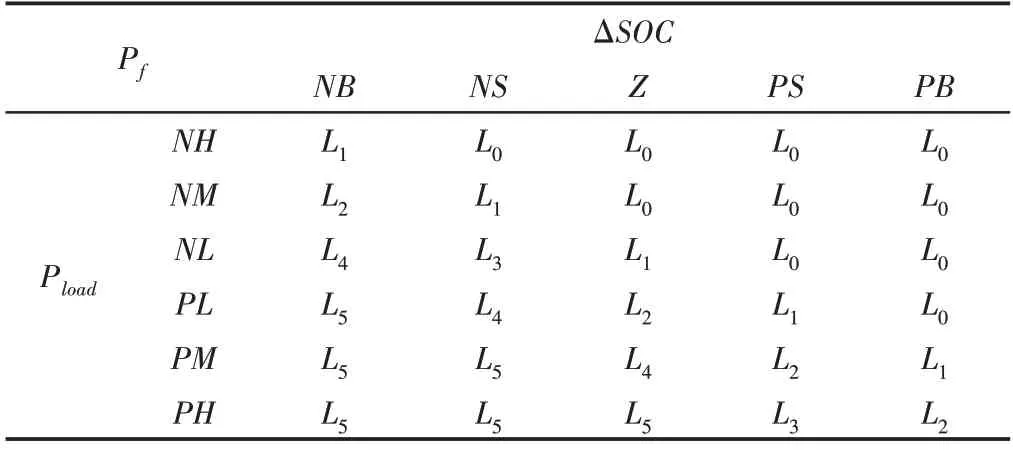
表2 模糊规则Tab.2 Fuzzy Rules

4 模糊控制策略优化

整车模型含有较多非线性模块，进行整车经济性仿真所需时间较长，且由于设计变量较多，导致优化所需的计算与时间成本过高。为了提高优化效率，可在保证拟合精度的前提下建立近似模型。常用的近似模型方法主要包括多项式模型、响应面模型、Kriging 模型以及神经网络模型，神经网络模型具有很强的逼近复杂非线性函数的能力，且具有较强的容错能力，可作为“黑箱”使用［11］。整车控制是高度非线性系统，可选用椭球基神经网络近似模型进行拟合。

4.1 敏感性分析

由模糊控制器可知，隶属函数可优化变量共有22个，同时动力电池SOC的目标值SOC*对整车经济性影响较大，所以模糊控制策略共有23个待优化变量。由于不同变量对等效氢耗的贡献率不同，可通过计算参数贡献率筛选优化变量，减少设计变量的个数，提高近似模型的精度与优化效率。

将输入变量归一化到［-1，1］，利用最小二乘法拟合模型系数记为Si，将Si转化为对等效氢耗的贡献率百分比，能更好地反映每个输入变量对响应的贡献［12］。各变量对等效氢耗影响结果的Pareto图，如图3所示。其中，各变量对等效氢耗的贡献率，如图3（a）所示。包含交互效应的各变量对等效氢耗的贡献率，如图3（b）所示。图中实体柱表示正相关，斜线柱表示负相关。综合考虑响应结果，选取X05、X07、X08、X10、X11、X12、X14、X17、X18、X19、X22和SOC*这12个设计变量作为模糊控制策略的优化变量，其初始值与设计空间，如表3所示。通过观察发现变量均处于模糊控制关键区域，符合工程经验。

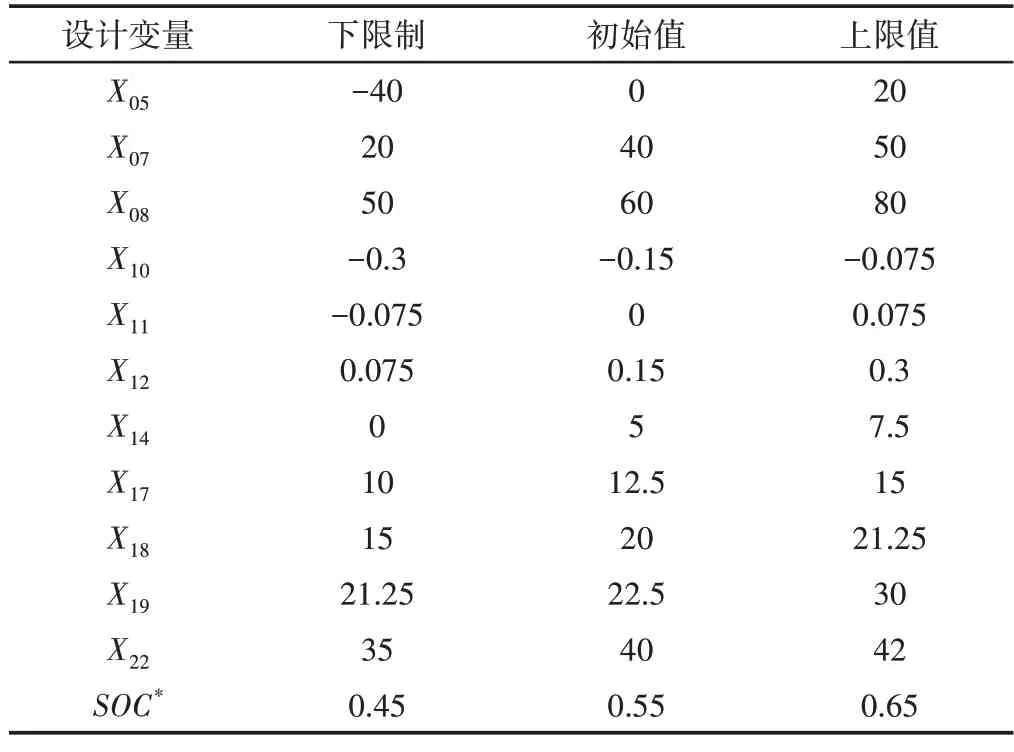
表3 设计变量设计空间Tab.3 Design Space of Design Variables

4.2 椭球基神经网络近似模型的建立

椭球基神经网络模型（EBFNN）是一种模拟生物神经系统，并利用人工神经元对信号进行识别、处理的数学模型，由输入层、隐层和输出层组成的一种前馈型神经网络［13］。

隐层椭球基神经单元的净输入及净输出可用下式表示：

式中：zj，i—椭球单元函数的初始半轴长；wjb，i—椭球基神经单元对于输入单元的半轴长；wjc，i—椭球基神经单元对于输入单元的中心；α—Sigmoid 曲线的斜率调节参数，其值越大，椭球基函数单元输出值逼近零的速度越快。

利用仿真获得的样本数据对椭球基神经网络进行训练，建立近似模型。为了验证近似模型的准确性，在设计空间随机选取20个采样点，并用采样点仿真值与近似模型观测值评估近似模型的可信度。其误差检验值，如表4所示。各种误差检验值均在允许范围内，说明基于椭球基神经网络近似模型能够较好地替代仿真模型进行优化。

表4 近似模型检验误差Tab.4 Inspection Error of Approximate Model

4.3 多岛遗传算法参数优化

由于模糊控制器中隶属函数与模糊规则的制定主要靠工程实践经验，具有较大的主观性，使燃料电池经济性能很难达到全局最优。模糊规则采用条件语句给出，难以进行参数化，容易造成优化后的结果不符合燃料电池汽车能量分配原则，所以隶属函数参数可作为主要的优化变量。

遗传算法属于全局优化算法，容易在某个极值点处过早收敛，从而造成“早熟”现象。而多岛遗传算法的本质是并行遗传算法，通过岛间个体迁移可使算法跳出局部最优解的限制，同时保证了种群及基因的独立性和多样性，极大地扩展了搜索范围，提升了算法的全局搜索能力和收敛速度［14］。这里采用多岛遗传算法进行优化，以提高燃料电池汽车经济性能。其优化问题可用下式表示：

优化设计初始种群个数设定为10，岛数设定为10，总进化代数设定为50代，整个优化过程中需迭代5000次。其优化迭代过程，如图4所示。可以看出在整个优化过程中，等效氢耗呈下降趋势，说明该算法具有良好的寻优功能。

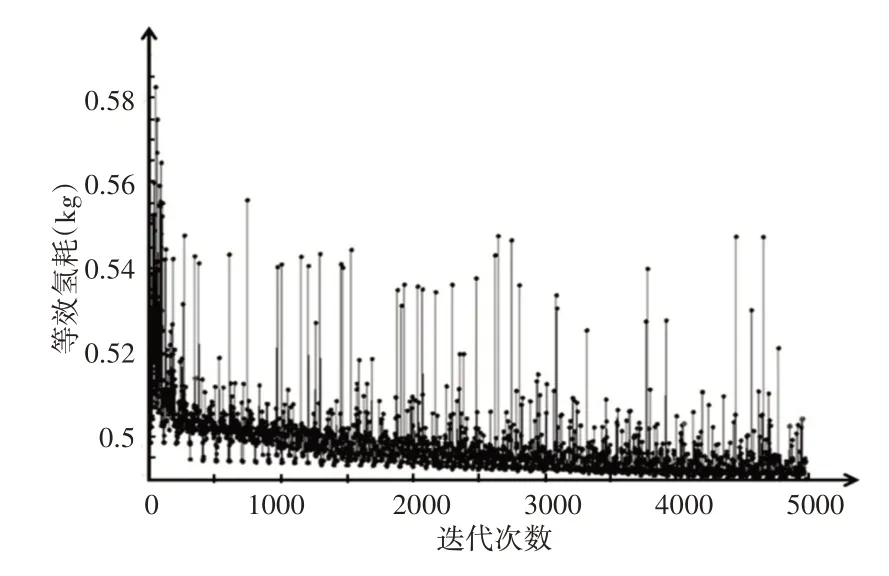
图4 多岛遗传算法迭代过程Fig.4 Iterative Process of Multi-Island Genetic Algorithm

利用多岛遗传算法对利用敏感性分析筛选出的12个待优化设计变量进行优化的结果，如表5所示。

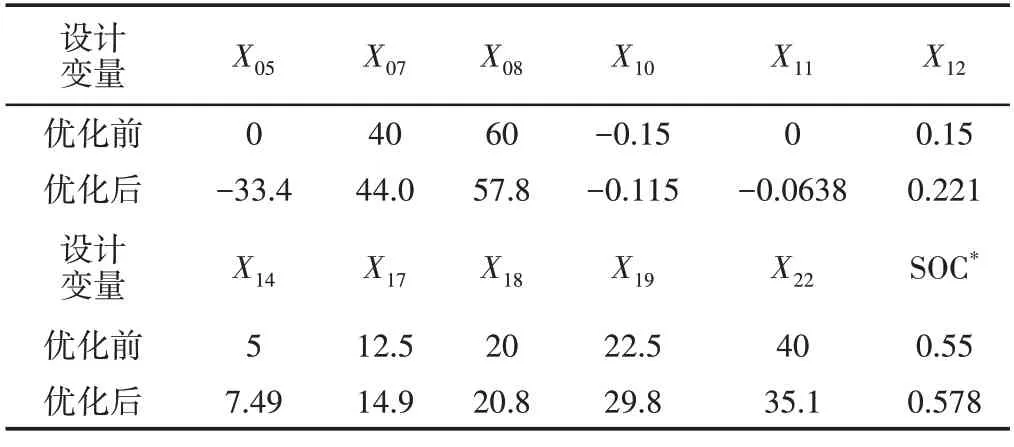
表5 设计变量优化结果Tab.5 Optimization Results of Design Variables

5 仿真分析

将12个设计变量的优化结果应用于模糊控制策略，基于整车模型和中国货车工况（CHTC_HT）进行仿真结果，如表6所示。表中m1表示优化前等效氢耗仿真值；m2表示优化后近似模型等效氢耗观测值；m3表示优化后等效氢耗仿真值；SOCb表示优化前SOC变化量；SOCa表示优化后SOC变化量。优化前后燃料电池系统输出功率、效率和SOC对比曲线，如图5～图7所示。

表6 优化结果Tab.6 Optimization Results

图5 燃料电池系统输出功率对比Fig.5 Comparison of Fuel Cell System Output Power

图6 燃料电池系统效率对比Fig.6 Comparison of Fuel Cell Systems Efficiency

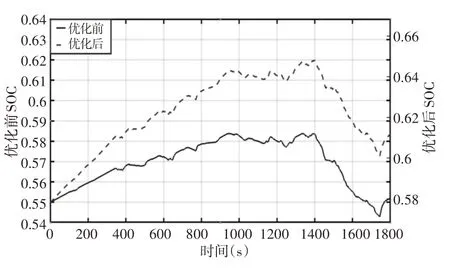
图7 SOC曲线对比Fig.7 Comparison of SOC Curve

由表6 可以看出，使用近似模型的观测值与仿真值相差0.0049kg/100km，其误差为0.15%，说明近似模型的精确度较高。百公里等效氢耗相较于优化前减少了0.2591kg，降低了8.4%，提高了整车经济性。根据图5～图7可知，当Pload小于燃料电池系统最佳效率点时，燃料电池基本处于最佳效率点工作，当Pload大于燃料电池系统最佳效率点时，Pf随负载在燃料电池系统最佳效率区变化，燃料电池系统效率高于45%。优化后Pf值变化范围明显减小，燃料电池工作更稳定，有利于提高燃料电池的寿命。虽然较于优化前SOC变化量与变化范围均有所提高，但整个循环工况下SOC值仍处于适宜区间，同时也体现了适当牺牲动力电池保护燃料电池的优化理念。

6 结论

这里针对某款中型燃料电池物流车，搭建了仿真模型。以整车需求功率和SOC变化量作为输入，燃料电池系统输出功率作为输出，建立了模糊控制策略，利用近似模型和多岛遗传算法进行了优化，并基于CHTC_HT工况进行对比仿真，得出以下结论：

（1）通过仿真验证了所建整车模型、模糊控制策略和优化方法的有效性。

（2）采用敏感性分析减少了设计变量个数，并将椭球基神经网络近似模型首次应用于该领域，提高了优化效率，为该领域的优化问题提供了参考。

（3）优化后燃料电池系统输出功率更加平稳，有利于提高其寿命，百公里等效氢耗较优化前降低了8.4%，提高了整车经济性。