基于点球约束的机器人误差建模与参数辨识

刘 毅，金晖力，丰宗强，易旺民，姚建涛*，赵永生

(1.燕山大学 河北省并联机器人与机电系统实验室, 河北 秦皇岛 066004；2.中国空间技术研究院 总装与环境工程研究所, 北京 100094)

机器人的定位精度主要包括重复定位精度和绝对定位精度[1]。目前，重复定位精度要优于绝对定位精度，重复定位精度范围为±2.00～±0.01 mm，而绝对定位精度相对较低，根据构型、负载及环境的不同，其范围为±100.0～±0.1 mm[2]。对于装配机器人，绝对定位精度过低，容易导致装配过程中零部件之间发生碰撞[3]。

机器人运动学建模是研究机器人误差补偿技术的理论基础。焦国太[4]使用了MD-H方法构建误差模型。赵瑞文[5]提出一种以MCPC模型为基础的MD-H建模方法。齐俊德等[6]提出基坐标系与测量坐标系之间在转换时存在误差。在机器人标定过程中，使用测量仪器被称为开环法。Oh[7]引入球杆仪对机器人的关节进行了测量。Jin等[8]应用自动经纬仪与三坐标仪对所标定机器人的末端进行标定测量。Wang等[9]应用激光跟踪仪对机器人的关节进行了测量。Joubair等[10]通过接触式探针测量4个正交平面以完成机器人标定实验。李永泉等[11]使用视觉系统进行运动学标定。开环法中所应用到的测量仪器精度较高，但其价格相当昂贵，测量仪器会受到测量空间的限制，对测量环境要求较高。因此，有学者[12]提出了闭环标定方法，通过对机器人施加物理约束，使机器人由开环链转变为闭环链，确定约束与误差模型之间的数学关系，通常又被称作自标定。相比于开环法，闭环法无需借助任何测量设备，成本低、操作简单、被广泛应用于工业生产中[13]。

误差参数辨识的过程是利用测量所得到的数据求解出各运动参数误差值，准确地分离至机器人的各个关节。对于定位精度来说，其过程为逆向求解机器人的各连杆参数，本质为求解非线性方程组得到最优解[14]。最小二乘法[15]是误差参数辨识常用方法之一，该方法原理简单，编程方式简便。Park等[16]利用拓展卡尔曼滤波法对机器人进行了误差参数辨识，并采用自学习算法对机器人的运动学模型进行参数辨识。奚陶[17]利用极大似然估计法对机器人进行了误差参数辨识。洪鹏等[18]应用LM算法，采用空间网格化的变参数误差模型算得机器人的柔性关节的误差参数近似值。Wang等[19]应用神经网络算法对机器人进行标定。唐越等[20]通过建立MD-H运动学参数误差辨识模型，结合激光跟踪仪对误差参数进行了辨识。Li等[21]应用遗传算法对机器人的误差参数进行辨识。郑方燕等[22]采用基于遗传算法的时栅误差参数辨识方法，有效地减少时栅传感器的二次误差与四次误差。Gao等[23]应用最小二乘法确定了机器人运动学误差参数的具体值。误差补偿包括直接补偿与间接补偿两种方式，间接补偿是对机器人的运动学参数进行补偿。高贯斌等[24]应用关节空间插值对机器人进行误差补偿，对机器人的误差补偿效果显著。张国庆等[25]采用数值法对机器人运动学模型进行调整，补偿后机器人的精度大幅度提高。但是，上述机器人误差辨识与补偿方法存在测量数据准确度要求高、数据量需求大、计算量较大等问题，如何建立数据采集精度高、自动化程度高、通用性强的机器人标定、误差辨识与补偿方法还有待研究。

本文提出了一种点球约束误差补偿方法，采用球面作为机器人末端约束，并在机器人末端加装6维力传感器使标定锥在接触到球面便停止运动，采集得到机器人运动关节数据。针对自主研制的7自由度装配调姿机器人，由D-H法建立正运动学模型，应用固定关节法与反变换法建立机器人逆运动学模型。构建7自由度装配机器人的误差模型，提出一种采用球面作为机器人末端约束的新型点球约束误差补偿方法。机器人末端采集点与球面进行多次接触，采集机器人各关节的数据，应用遗传算法辨识误差参数，将辨识得到的参数代入机器人的误差模型中，将补偿前后的机器人运动学模型进行对比，确认机器人定位精度是否得到明显提高。

1 7自由度装配机器人运动学分析方法

7自由度装配机器人，主要应用于舱内设备总装的舱内装配环节，具有7个自由度，其中，第1自由度、第2自由度、第5自由度为移动自由度，其余为转动自由度，7自由度装配机器人结构3维模型如图1所示。

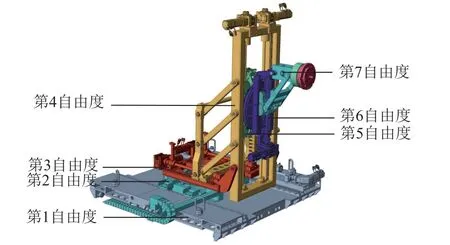
图1 7自由度装配机器人3维模型Fig.1 3D model of the 7-DOF assembly robot

7自由度装配机器人负载较大，为满足刚度需求，丝杠、导轨大部分采用对称设计方案，可以在很大程度上提高机器人整体刚度。第4自由度翻转架结构在原始曲柄滑块结构的基础上加入了带有虚约束的平行四边形结构，在保证原有运动不变的基础上，增加了该结构的刚度。

根据D-H参数法分别建立基坐标系与连杆坐标系，如图2所示，参数见表1（变量含义见附录A）。

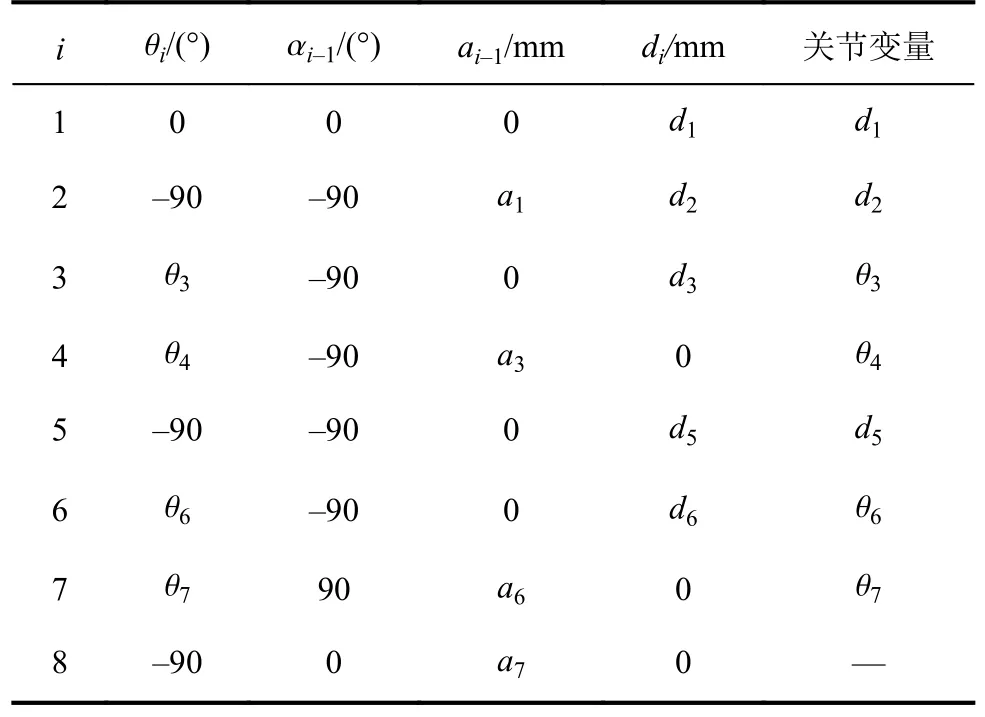
表1 装配机械臂D-H参数Tab.1 D-H parameters of assembly robot

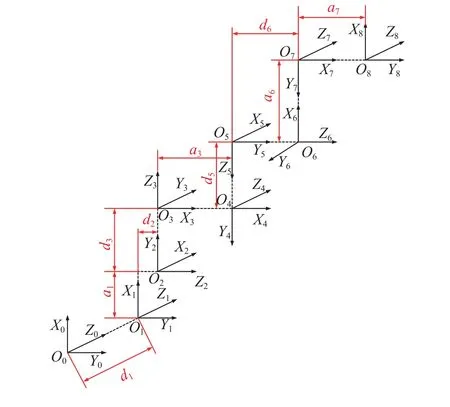
图2 7自由度装配机器人D-H坐标系Fig.2 D-H coordinate system of 7-DOF assembly robot

表1中，i为关节序号，i=1～8，a1=169 mm，d3=284 mm，a3=545 mm，d6=214 mm，a6=320 mm，a7=245 mm。

式中，T为位姿变换矩阵，q1～q8为转动变量，d1～d8为移动变量。

式（2）～（3）中，

式（1）和（2）计算得到的4×4矩阵为冗余自由度装配机器人的运动学位置正解方程。将各运动关节的关节变量依次代入正解方程，即可得到机器人末端工件坐标系相对于大地坐标系的位姿矩阵。

针对7自由度关节冗余，存在无穷多组运动学逆解的问题，本文采用固定第2转动机构自由度θ4，由坐标反变换法推导位置运动学逆解方程，得到关于θ4的逆运动学解析函数。令式（1）等号左侧为B，等号右侧为A，两矩阵部分位置元素值相等。因此在固定第二转动关节变量θ4的情况下，可以通过矩阵反变换的方式对各关节进行推导,结果如式（5）所示：

式 中：l、φ为中 间 变 量，lcos ϕ=cos θ4sin θ6+sin θ4，lsin ϕ = -cos θ4sin θ6+sin θ4，ay=l2+ sin ϕ2，az=l2+cos ϕ2。

2 误差补偿方法与误差模型的建立

运动学标定是通过误差建模、参数辨识、误差补偿等步骤将修正后的D-H参数输入机器人控制器，从而减小理论模型与真实模型的误差、提升末端装配精度的过程[26]。本文在采用传统误差建模的前提下，提出点球标定方法，并通过遗传算法对误差参数进行辨识，最终将辨识所得误差参数代入误差模型中。

2.1 点球约束误差补偿方法

基于点约束的传统物理标定方式，采用球面作为机器人末端约束，使机器人末端采集点与球面进行多次接触，在采集点使用智能算法对D-H参数的误差值进行辨识，将误差值代入误差模型中得到完整的机器人末端误差模型。相较传统点约束标定方法，减小了进行点对点接触所产生的误差。

机器人点球约束误差补偿方法步骤如下：

1）在机器人运动学正解模型的基础上，建立含有误差值的运动学误差模型0ET（E为标定锥尖点）。

2）在机器人可达工作空间内，放置一靶标球并测得球心在机器人基坐标系下的位置。在机器人末端加装6维力传感器，在6维力传感器末端安装标定锥。控制机器人以不同姿态使标定锥与靶标球球面重合，如图3所示，读取n组标定锥与靶标球球面重合时的关节值。

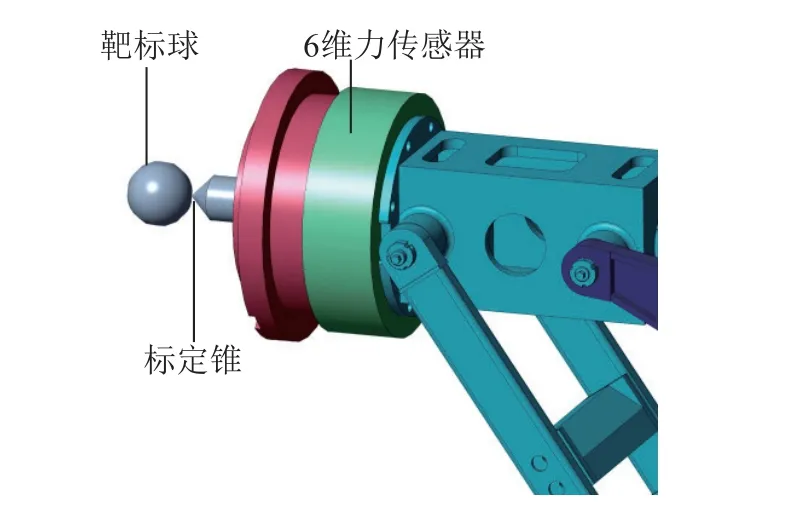
图3 标定锥与靶标球球面重合示意图Fig.3 Spherical coincidence of calibration cone and target sphere diagram

3）将读取的n组机器人关节值代入机器人运动学误差模型0ET，得到n组含有误差值的4×4齐次变换矩阵。

4）提取齐次变换矩阵中位置参数P=[px py pz]T，P为标定锥在n次对接靶标球相对于基坐标系的位置关系，可以得到n个点，构成空间点集。

5）以靶标球球心为球心，距离球心最远点到球心距离为半径R，将所得的n个点都包含在一个球体内。

6）用遗传算法，确定适应度函数为靶标球球体半径R，计算各个D-H参数的偏差值。

7）将D-H参数的偏差值代入机器人运动学误差模型0ET中，得到补偿后的运动学误差模型。

8）对比补偿前后的机器人定位精度，验证该补偿方法是否有效。

2.2 基于D-H模型的机器人末端误差模型

将运动学各参数的偏差代入运动学D-H模型中，得到含有偏差δ的运动学误差模型见表2。

表2 含有偏差的运动学D-H模型参数Tab.2 Kinematic D-H parameters with deviations

在考虑D-H参数偏差的情况下，连杆变换矩阵可以写为：

在标定锥锥尖建立标定锥坐标系，使标定锥坐标系方向与机器人末端坐标系方向一致，如图4所示。标定锥为精加工件，标定锥锥尖到机器人末端距离误差很小，对整体标定结果的影响可以忽略不计，通过3维模型可测得标定锥坐标系相对于第7自由度坐标系的位置坐标，可得标定锥坐标系与第7自由度坐标系间的位姿变换矩阵为：

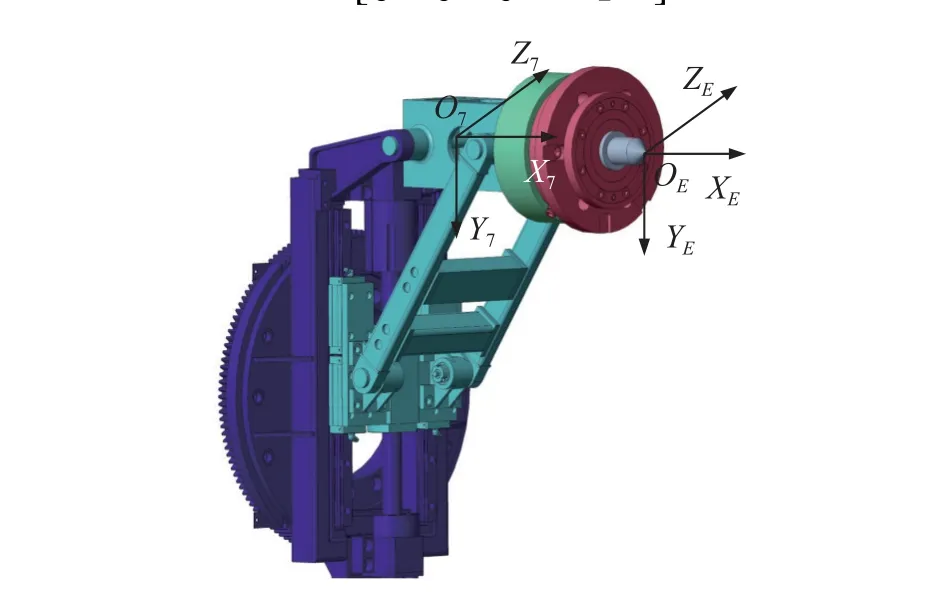
图4 标定锥坐标系示意图Fig.4 Schematic diagram of the calibration cone coordinate system

故机器人运动学误差模型为：

误差模型中，待辨识的误差参数共有28个：

3 参数辨识

3.1 基于牛顿迭代法的关节值获取

在实际标定过程中，在机器人工作空间内设置一固定不动靶标球，控制机器人末端标定锥以不同位姿对接靶标球，当标定锥接触靶标球时，通过6维力传感器反馈至控制器，使机器人停止运动。理论分析角度进行研究时，对位姿变换矩阵与D-H参数偏差值进行预设定处理，在此基础上对运动关节值进行辨识研究。

机器人3维模型中，在机器人工作空间内，固定一个半径R=25.5 mm的靶标球，使靶标球相对于机器人基坐标系位置不变。靶标球球心相对于基坐标系的位置为0T P=[1 156.43,1 124.31,0.36]T，控制机器人以不同位姿使标定锥锥尖与靶标球球面重合，通过该方式获得20组位姿变换矩阵0ETip（i=1,2,···,20），如附录A表A1所示。

由于理论验证环节无法直接获取机器人各自由度关节变量值，故预设定D-H参数误差值求解各自由度关节变量值。预设定D-H参数中除关节变量值的参数误差见表3。

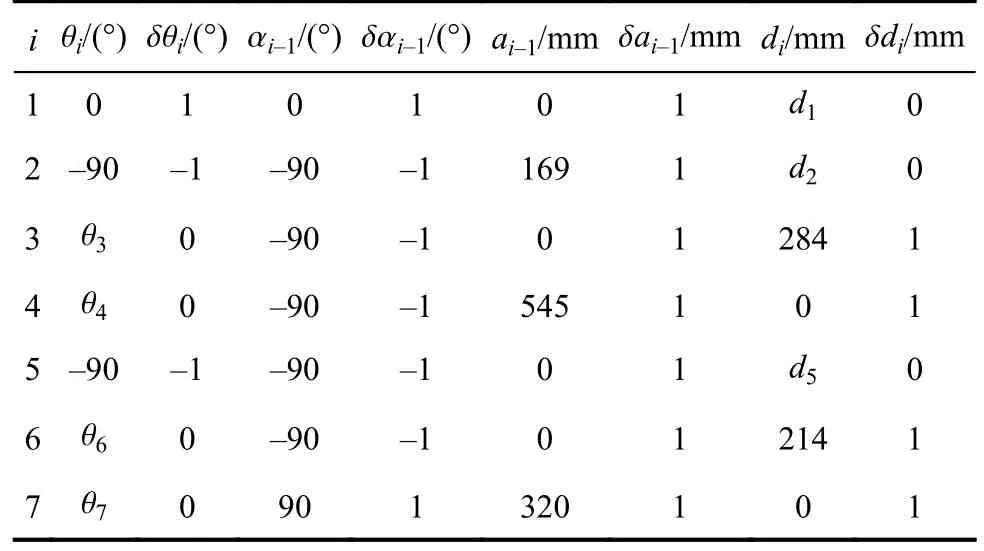
表3 D-H参数理论值与预设定误差值Tab.3 Theoretical values of D-H parameters and preset error values

正解计算的实质是求解多元耦合非线性方程组。对于求解这类问题，使用解析方法通常不能求得准确解，且所得解析解往往包含多组结果，难以通过判断条件筛选出正确的机器人位姿，故采用数值方法求取近似解，在此引入牛顿迭代法进行求解。牛顿迭代法计算速度快[27-28]，其公式为：

计算流程图如图5所示。

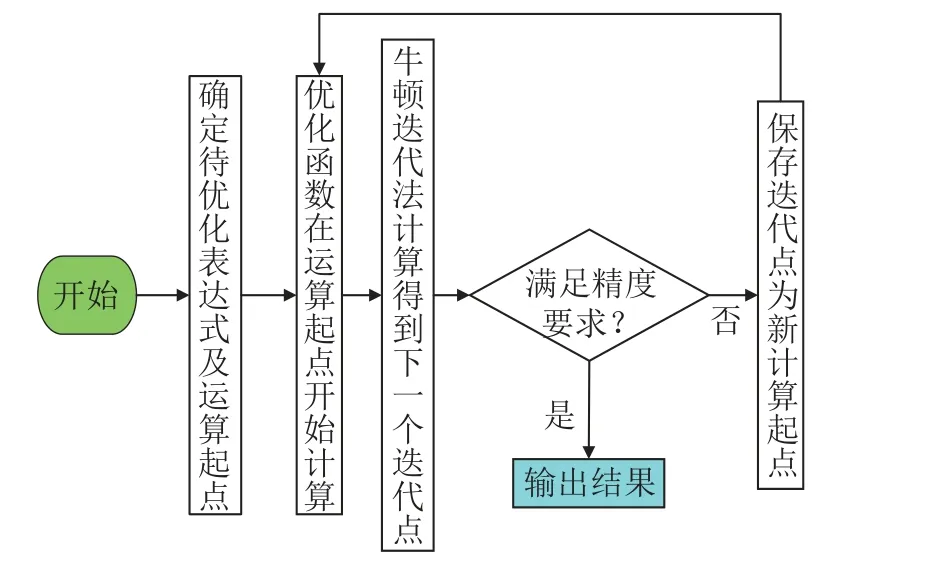
图5 牛顿迭代法运算流程Fig.5 Newton's iterative algorithm flow chart

将表3中预设定的误差值代入式（8），所得到的只含有各自由度关节变量的位姿变换矩阵为（i=1,2,···,20），构造牛顿迭代法的优化表达式为：

式中，e表示关节变量含偏差，p表示只含有关节变量不含偏差。在Matlab中，按照图5中描述的运算流程编写牛顿迭代法程序，设置精度范围为 ξ=10-4，求解结果见表4。

表4 牛顿迭代法求解的运动关节值Tab.4 Newton's iterative method for solving the kinematic joint values

将求解结果代入式（1），选取表4中的第4、8、9、20组，正运动学求解结果见表5。

表5 正运动学求解结果Tab.5 Positive kinematic solution results

对比表4和表5中第4、8、9、20组矩阵可知，求解的位姿变换矩阵与预设定的位姿变换矩阵基本相同，误差在10-11之内，通过牛顿迭代法求解非线性方程组的关节变量值，求解结果误差极小。

3.2 基于遗传算法的误差参数辨识

遗传算法遵循“适者生存”的原则，在计算过程中，设置28个偏差参数为初始种群，在初始种群中，不断地进行交叉运算，环境适应度低的值被剔除种群，环境适应度高的值形成新的种群，当所得到的种群满足终止条件时，停止计算。

通过Matlab中遗传算法工具箱对28个误差参数值进行辨识，通过式（8）和表4可以得到含有误差参数 δ的位姿变换矩阵0ETie(δ)（i=1,2,···,20） ，0ETie(δ)表示标定锥锥尖点接触靶标球球面时的位姿，根据0ETie(δ)，应用遗传算法可以求解出无限逼近于真实值的近似值。

约束条件（适应度函数）为球体半径R。控制机器人以不同位姿使末端标定锥与靶标球球面接触，在标定锥与靶标球将要接触时，降低机器人运动速度，在标定锥锥尖刚接触靶标球时，6维力传感器反馈末端受力情况，并传递至机器人控制器，机器人停止运动。将表4中对接20次的20个标定锥锥尖点定义为空间点集{P}，依据最小包围球原理，使点集{P}中的所有点包含于空间球体中，并且球体半径R最小，得到包围球半径R和误差参数δ之间的函数关系式，即适应度函数，如式（11）所示：

应用遗传算法求解误差参数的基本流程为：

1）编码并随机产生多个初始群体。

2）确定适应度函数，将每一代新的种群与上一代种群中的数据进行对比，淘汰适应度低的数值，保留适应度高的数值，进行下一步遗传运算。

3）在遗传运算中逐步生成新的种群，满足终止条件后停止运算。

4）挑选后代种群中各个误差参数适应度最低的数值作为最终结果输出。

应用遗传算法求解误差参数的流程如图6所示。

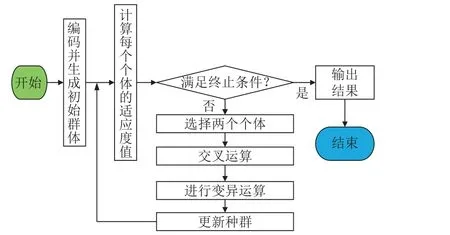
图6 遗传算法运算流程Fig.6 Genetic algorithm flow chart

应用Matlab中遗传算法程序进行误差参数辨识，经过迭代计算2 336次后，预设适应度函数得到最小值0.364 4，平均值为0.482 7，如图7所示。误差参数辨识具体数值见表6。

表6 预设误差参数辨识结果Tab.6 Identification results of preset error parameters

图7 预设适应度函数值变化趋势Fig.7 Trend of adaptation for preset

将表3中预设误差值与表6中辨识误差值进行对比，可以看出，预设误差值与辨识误差值基本相同，说明基于遗传算法的误差参数辨识方法有效。

将得到的辨识误差值代入运动学误差模型中，将表4的关节值分别代入运动学理论模型0ET和运动学误差模型0ETe中，可以得到两组空间点集 {P1}和{P2} ，将 {P1} 和 {P2}与靶标球组合在一起，以靶标球球心为包围球球心，以最小的包围球将空间点集中所有点都包络进去，求解得到包围球补偿前半径为50.236 mm，补偿后半径为25.864 mm，如图8所示，除去靶标球自身半径R=25.5 mm，可知机器人误差减小了98.52%，绝对定位精度大幅度提高，标定效果显著。

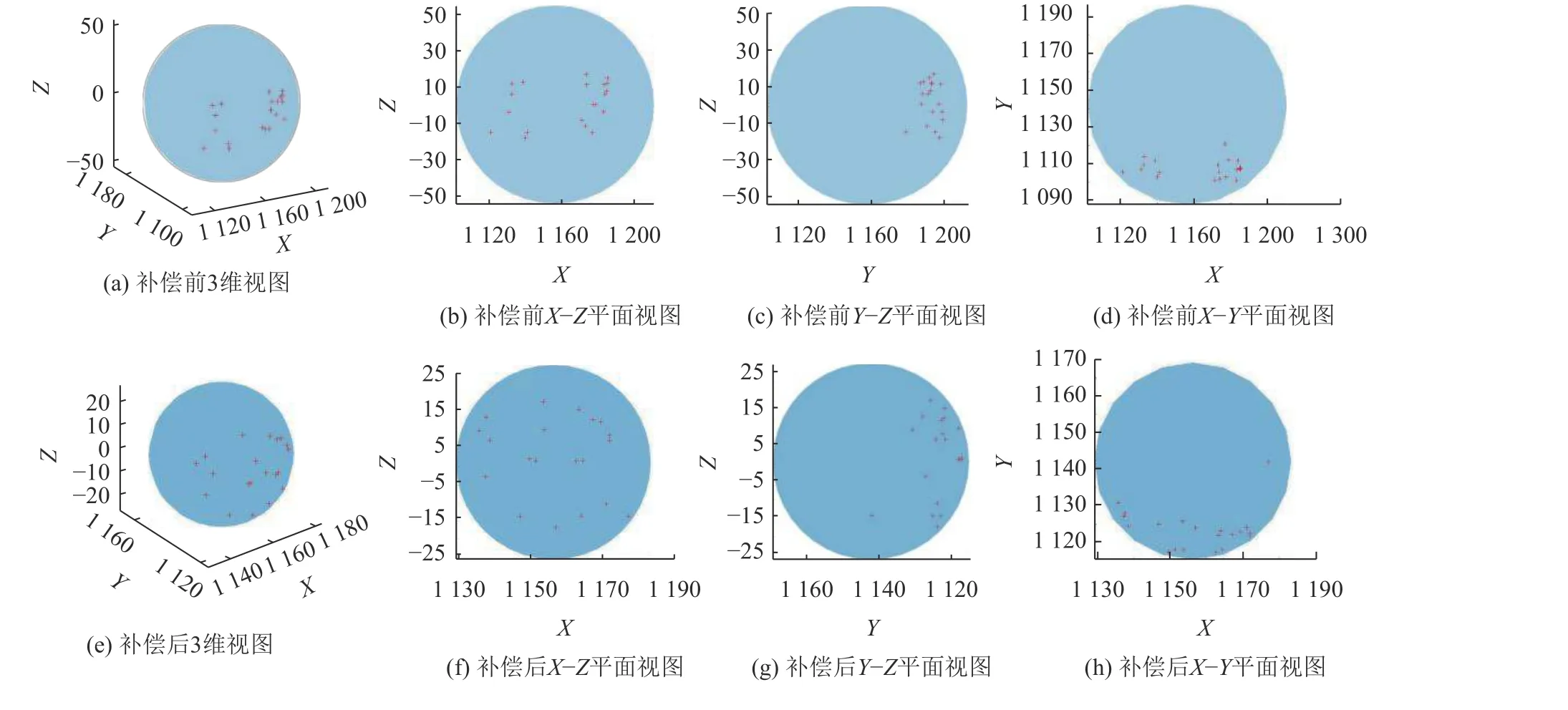
图8 补偿前/后标定锥尖点包围球Fig.8 Calibration cone tip point surround ball before/after compensation

4 误差补偿实验

在第3章误差补偿理论研究的基础上，进行机器人误差补偿实验。根据点球标定方法，采集机器人各关节运动量数据，应用遗传算法对误差参数进行辨识，再将辨识得到的参数代入机器人误差模型中，完成机器人误差补偿过程；分别采用了空间多靶标精度测试与基于激光跟踪仪测量的精度测试方法进行精度测试，验证所提出的误差参数辨识及误差补偿方法。

4.1 实验方案

7自由度装配机器人样机如图9所示。

图9 7自由度装配机器人样机Fig.9 Seven-degree-of-freedom assembly robot prototype

机器人末端加装6维力传感器，用于传递机器人末端标定锥受力情况。在6维力传感器末端安装零点定位器，用于安装标定锥。零点定位器将所受的力传递给6维力传感器。零点定位器重复定位精度在0.005 mm内。

设计标定锥与零点定位器上定位销连接，通过将定位销连接机器人末端零点定位器实现在机器人末端加装标定锥。在靶标球安装板四周安装4个靶标锥，如图10所示。

图10 靶标球与靶标锥安装Fig.10 Target ball and target cone installation

实验方案如下：

1）建立含有误差参数的机器人误差模型0ETe，由运动学知识可知该误差模型共有28个误差参数 δ。

2）将靶标球和安装板固定在模拟舱中，并确定靶标球球面位于机器人工作空间内。

4）根据求得的含有误差参数的误差模型0ETe和实际测得的各关节位置，应用遗传算法的误差参数辨识方法辨识误差参数 δ。

5）将误差参数 δ代入到含有误差参数的误差模型0ETe中，得到补偿后的机器人误差模型0ETt，t表示补偿完成，与理论运动模型区分。

10）应用补偿前的运动学模型0ET，重复步骤3）～9）并测量标定锥锥尖点与靶标锥锥尖点距离，对比补偿前与补偿后的距离。

11）重复步骤1）～10），继续对靶标锥3、靶标锥4进行上述实验，记录补偿前后标定锥锥尖点与靶标锥锥尖点的距离并进行对比。

12）进行二次实验验证，应用激光跟踪仪根据国标[29]定义的位置精度检测方法进行实验验证，测量补偿前后的运动学模型机器人末端所到达的测量点并进行对比。

实验流程如图11所示。

图11 误差补偿实验流程Fig.11 Error compensation experiment flow chart

4.2 实验数据采集

将靶标球加装至安装板上并将安装板固定在模拟舱内，确保靶标球球面在机器人易到达的工作空间内。控制机器人运动使末端标定锥接触靶标球面，在接触过程中，先控制机器人使标定锥接近靶标球面，接近后采用点动模式，速度设置为0.05 mm/s，在标定锥刚接触到靶标球面时，机器人由6维力传感器反馈的信息直接停止机器人运动，在该状态下，记录机器人各关节量。标定锥与靶标球球面共对接30次，并采集这30次的机器人关节量。为使误差参数辨识的结果更准确，在标定锥对接靶标球球面的过程中，30组对接点应尽量均匀地分布在靶标球的球面上，所测数据见表7。

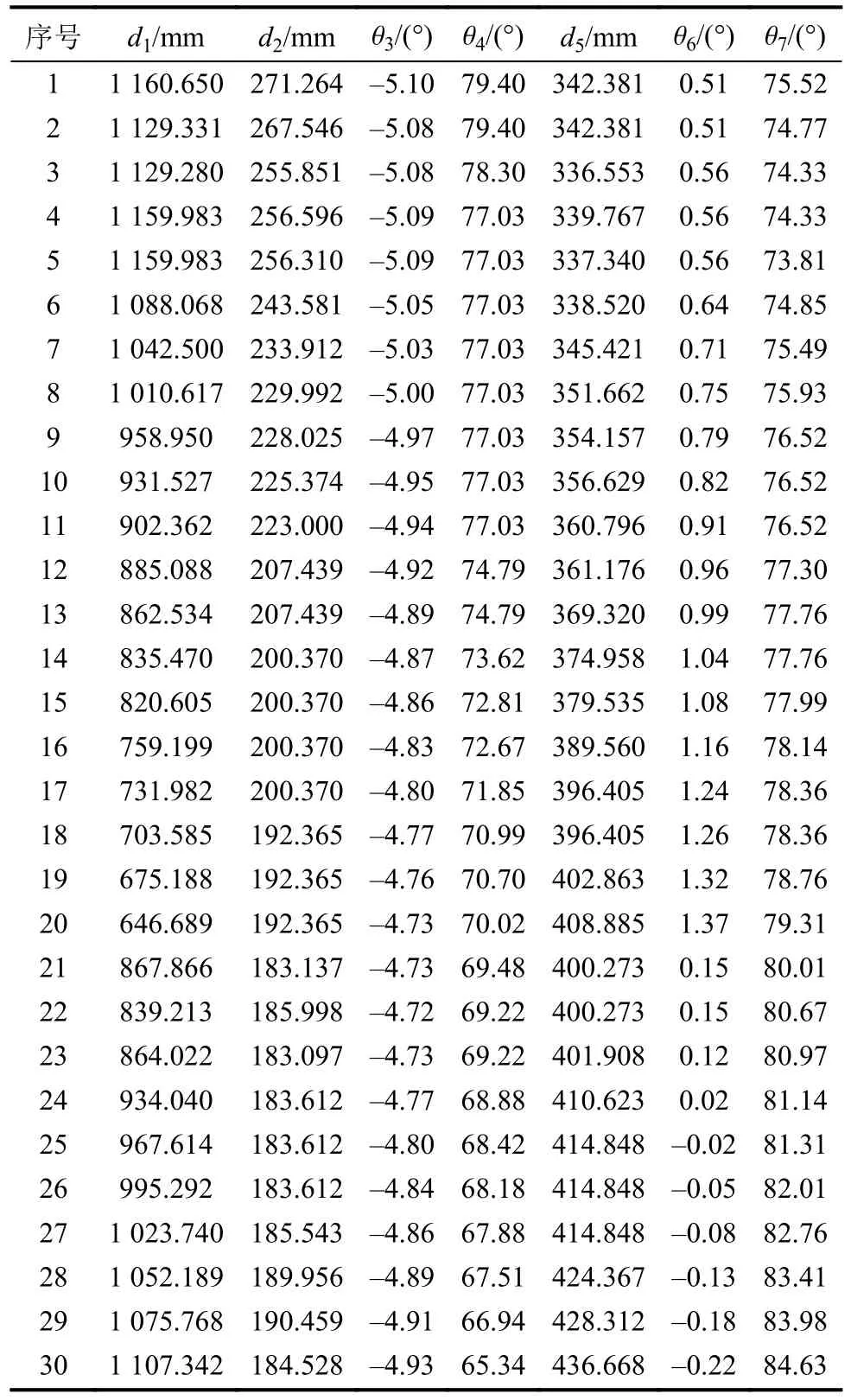
表7 对接靶标球各关节运动量Tab.7 Amount of movement of each joint of the docking target ball

4.3 误差参数辨识及误差补偿

根据上述所测实验数据，由遗传算法对误差参数进行辨识，在迭代计算1 865次后，实验适应度函数得到最小值0.394 6，平均值为2.396 5，由图12可知，当迭代计算约1 600次后，适应度函数的变化趋势趋于平缓，算法基本进入收敛状态。所得各参数具体值见表8。

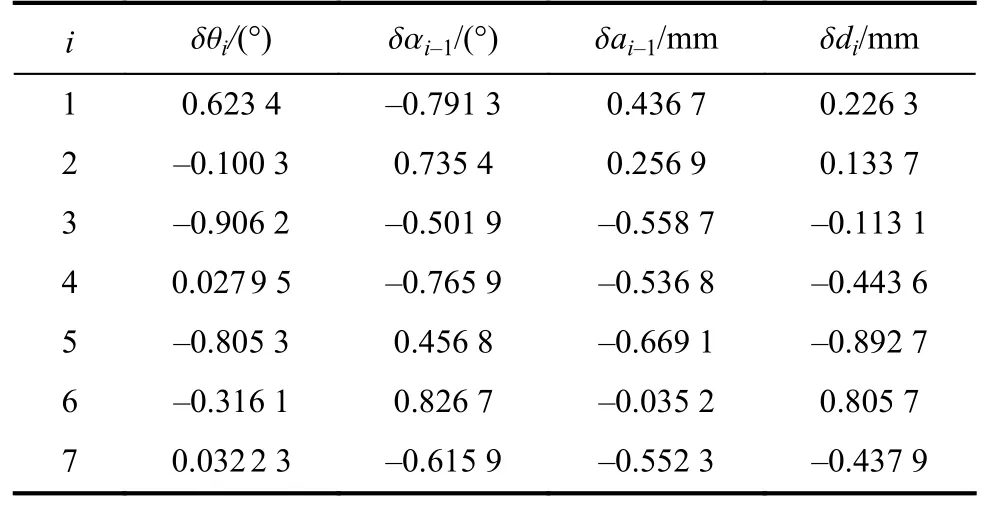
表8 实验误差参数辨识结果Tab.8 Identification results of experimental error parameters

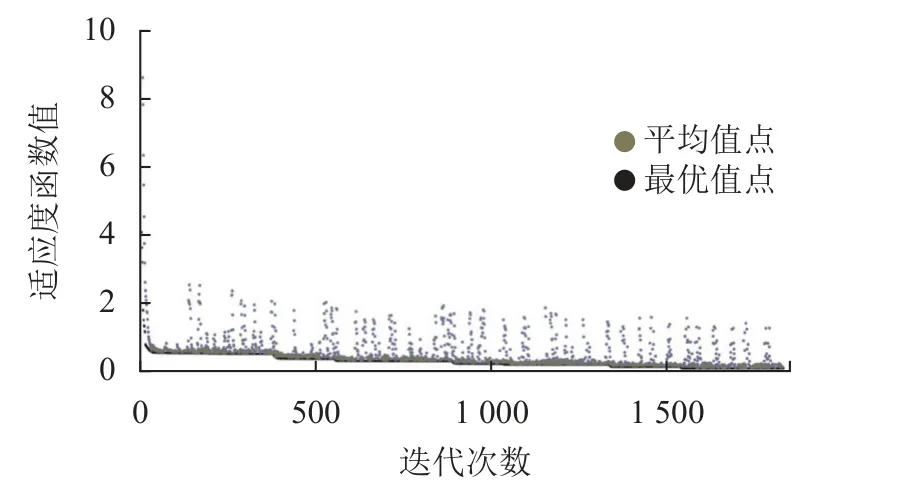
图12 实验适应度函数值变化趋势Fig.12 Trend of adaptation for experiment

将表8中所得误差参数辨识结果代入带有参数的运动学误差模型中，得到最终的机器人运动学误差模型。

4.4 精度测试

4.4.1 空间内多靶标锥精度测试

对比补偿前后标定锥到达点与理论点距离以直观地说明误差补偿的效果。在安装板上的靶标球四周安装4个靶标锥，使所选4个靶标锥锥尖点在空间3个方向均有差异，如图13所示。4个靶标锥以靶标球为中心两两对称，靶标锥2锥尖点在靶标锥1锥尖点X轴负方向70 mm，Y轴负方向5.5 mm，Z轴负方向70 mm处，靶标锥3锥尖点在靶标锥1锥尖点X轴负方向70 mm，Y轴负方向5.5 mm，Z轴正方向70 mm处，靶标锥4锥尖点在靶标锥1锥尖点X轴负方向140 mm处，靶标球、靶标锥坐标系与机器人基坐标系相同。

图13 靶标锥安装示意图Fig.13 Target cone installation schematic

将靶标锥1锥尖点坐标描述为P1=(x1,y1,z1)，则靶标锥2锥尖点相对于靶标锥1锥尖点坐标为：

靶标锥3锥尖点相对于靶标锥1锥尖点坐标为：

靶标锥4锥尖点相对于靶标锥1锥尖点坐标为：

在已知靶标锥1锥尖点的位姿变换矩阵的前提下，可以求出靶标锥2、靶标锥3、靶标锥4的位姿变换矩阵，如下所示：

控制机器人使标定锥锥尖点与靶标锥1锥尖点重合并采集各个关节运动量M1e，随机控制机器人各关节量，进行6次对接，所采集数据见表9。

表9 对接靶标锥1锥尖点机器人各关节量Tab.9 Docking target cone 1 cone tip point robot each joint volume

对靶标锥2锥尖点补偿前后的位姿变换矩阵应用牛顿迭代法求解，可以得到靶标锥2锥尖点补偿前后的各关节量，求解结果见表10和表11。

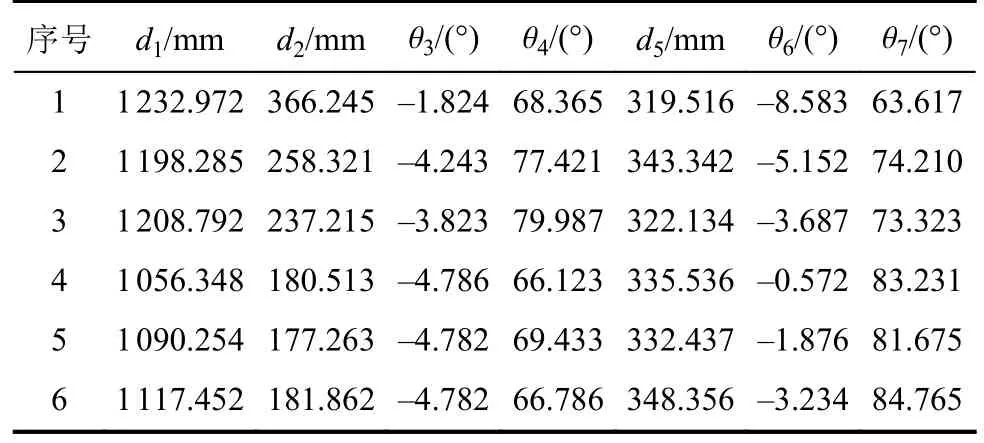
表10 补偿前靶标锥2锥尖点关节量Tab.10 Amount of joint at the tip of the cone of the target cone 2 before compensation

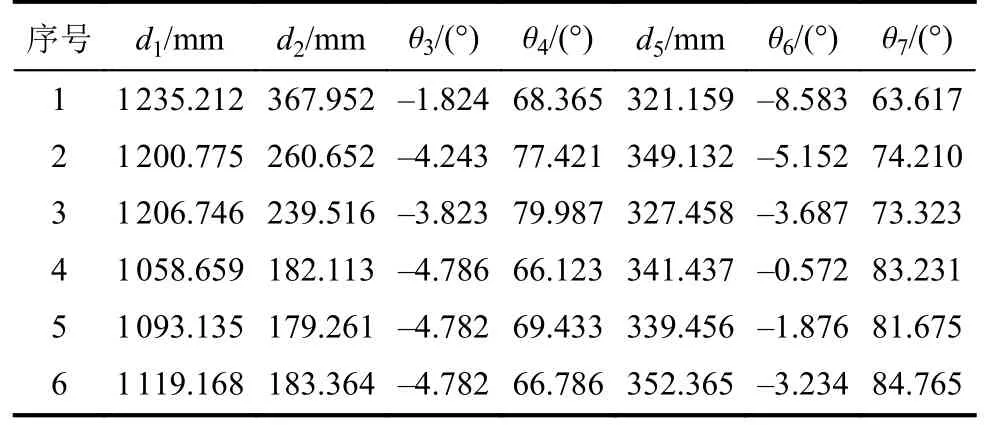
表11 补偿后靶标锥2锥尖点关节量Tab.11 Joint volume of the cone tip point of the target cone 2 after compensation

得到标定锥锥尖点与靶标锥2锥尖点重合时补偿前后的机器人各运动关节量，控制机器人按照表10、11所得运动关节量运动，使用数显游标卡尺对两个锥尖点进行测量，游标卡尺量程为0～300 mm，精度为0.01 mm，测量过程如图14所示。可以得到6组机器人补偿前后标定锥锥尖点与靶标锥2锥尖点的距离对比，为使实验结果更准确，对靶标锥3、4按照上述步骤再次进行实验，测量结果见表12。

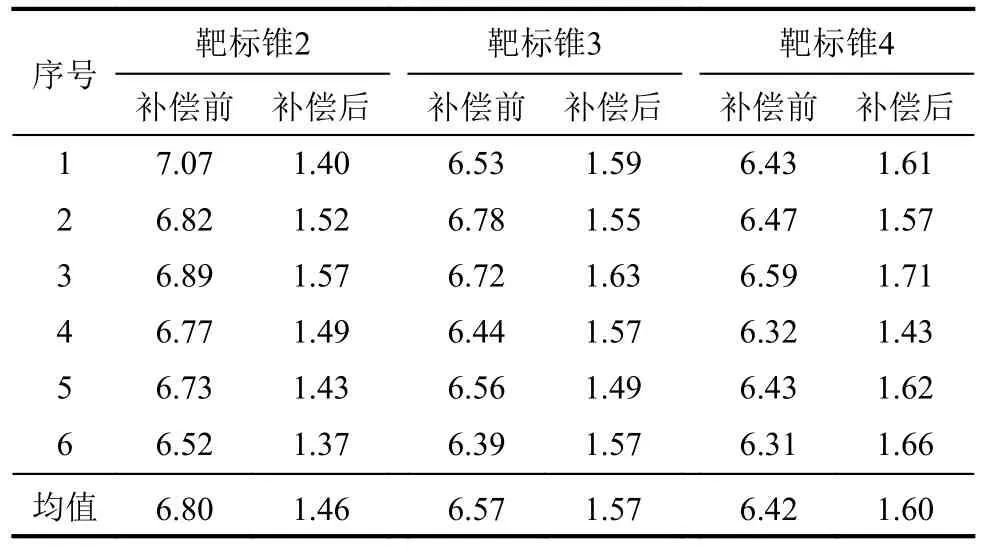
表12 补偿前后两锥尖点距离对比Tab.12 Distance comparison before and after compensation mm

图14 补偿前后两锥尖点距离Fig.14 Compensate the distance between two cone tip points before and after

从图14和表12可以看出补偿前标定锥与靶标锥的距离较大，补偿后标定锥与靶标锥的距离明显减小。标定锥对接靶标锥2时，补偿前的距离平均值为6.80 mm，补偿后的距离平均值为1.46 mm，平均误差减小了约78.53%。标定锥对接靶标锥3时，补偿前的距离平均值为6.57 mm，补偿后的距离平均值为1.57 mm，平均误差减小了约76.10%。标定锥对接靶标锥4时，补偿前的距离平均值为6.42 mm，补偿后的距离平均值为1.60 mm，平均误差减小了约75.08%。实验证明，基于遗传算法的误差参数辨识及误差补偿的机器人标定方法有效。

4.4.2 基于激光跟踪仪的精度测试

为进一步验证遗传算法的误差参数辨识及误差补偿方法有效，应用激光跟踪仪根据国标[29]定义的位置精度检测方法进行实验验证。实验选用FARO激光跟踪仪，型号为R80。国标[29]中位置精度的检验方法为：在机器人容易到达的工作空间内选择1个立方体作为检测区域，如图15所示，立方体的3条棱边与机器人的基坐标系方向一致，在立方体内选取1个最大截面C1C2C7C8，选取P1～P5为检测点。其中，P1为立方体的中心，P2、P3、P4、P5离端点距离为立方体对角线长度的（10±2）%。

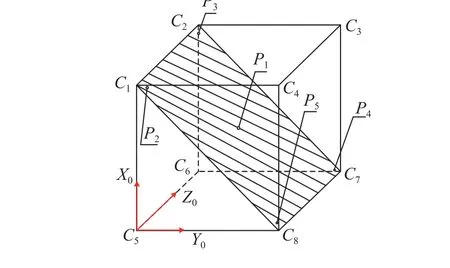
图15 立方体检测区域示意图Fig.15 Diagram of the cube detection area

驱动机器人的所有关节，设置循环路线为P1→P2→P3→P4→P5，应用补偿前的运动学模型进行30次循环运动，采用激光跟踪仪实时跟踪，记录每次到达检测点时机械末端的坐标信息，进而计算出补偿前这5个点在X、Y、Z方向上位置精确度，测量过程如图16所示。继续应用补偿后的运动学模型进行30次循环运动，计算出补偿后这5个点在X、Y、Z方向上平均位置精确度，计算结果见表13。

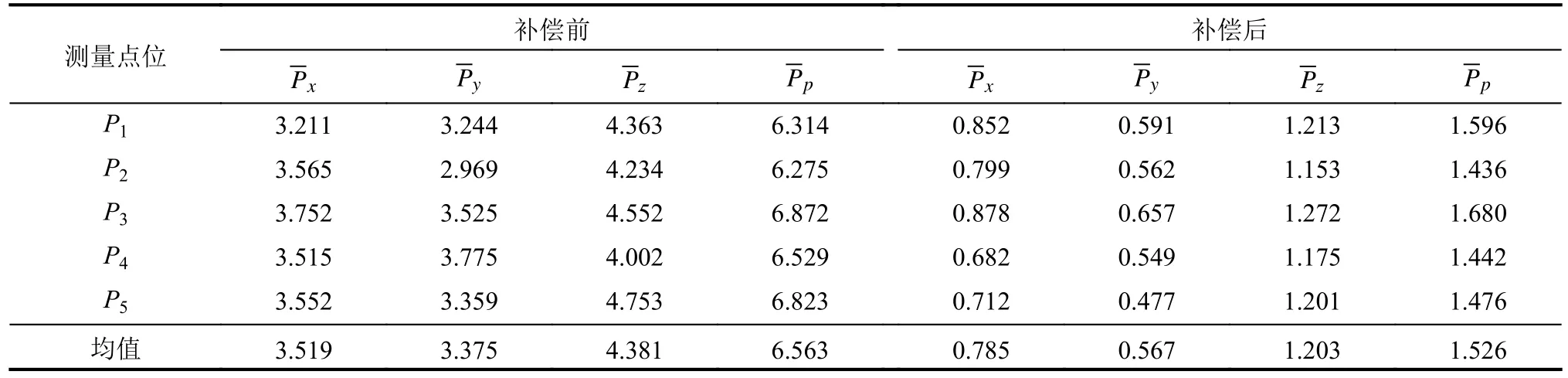
表13 补偿前后平均位置精确度Tab.13 Compensates for front-to-back position accuracy mm

图16 激光跟踪仪测量过程Fig.16 Laser tracker measurement process

由表13可知，与补偿前相比，补偿后的平均位置精度显著提升。X、Y、Z方向分别提升了77.69%、83.17%和72.53%。综上，基于遗传算法的误差参数辨识及误差补偿的机器人标定方法有效。补偿前后对比见图17。

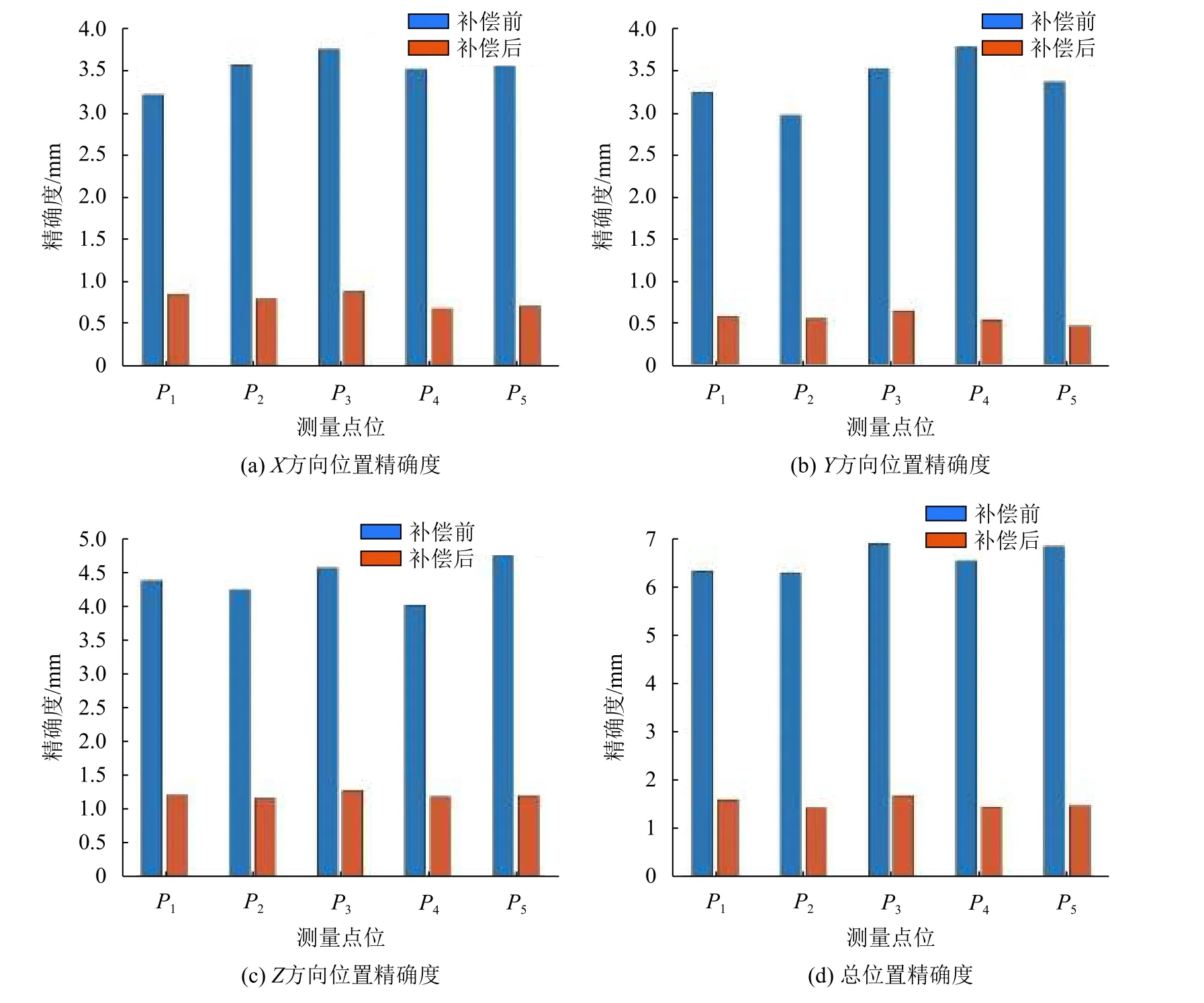
图17 补偿前后位置精度对比Fig.17 Comparison of position accuracy before and after compensation

5 结 论

本文以自主研制的7自由度装配机器人为研究对象，开展了机器人误差模型及误差补偿等方面的研究。在误差分析的基础上，提出了点球约束误差补偿方法，采用球面作为机器人末端约束，并在机器人末端加装6维力传感器使标定锥在接触到球面便停止运动，采集得到机器人运动关节数据，以靶标球球体半径为适应度函数，利用遗传算法辨识误差参数。实验证明装配机器人绝对定位精度提升76.74%，验证了点球约束误差补偿方法的有效性。该方法降低了测量过程中产生的误差，提高了数据采集精度，并且提升了机器人自标定自动化程度，具有通用性，可用于多自由度机器人误差参数辨识与补偿。

附录见本刊网络版（http://jsuese.ijournals.cn/jsuese_cn/ch/reader/view_abstract.aspx?file_no=202200493&flag=1），扫描标题旁的二维码可阅读网络全文。