基于竖缝隔板的大底坡鱼道水力优化数值模拟
邓 斌,黄姣凤,徐 拓,尹龙斌,张家强,蒋昌波
(1.长沙理工大学水利与环境工程学院,湖南 长沙 410114; 2.水沙科学与水灾害防治湖南省重点实验室,湖南 长沙 410114; 3.洞庭湖水环境治理与生态修复湖南省重点实验室,湖南 长沙 410114)
闸、坝等水利设施的兴建在给防洪、灌溉、缓解缺水、开发清洁能源等方面带来巨大效益[1]的同时会截断河流,导致完整的河流碎片化[2],阻断鱼类洄游通道并影响其种群繁殖[3]。鱼道作为一种生态型水利工程,能够重建河流连通性,帮助鱼类克服障碍恢复自然洄游[4],对保护鱼类资源及水生生物多样性具有一定的积极作用。鱼道主要有仿自然型鱼道(仿自然鱼梯、鱼坡和过鱼旁路等)和技术型鱼道(竖缝式鱼道、池堰式鱼道和丹尼尔鱼道等)两种类型[5],其中竖缝式鱼道因结构简单、能适应多变的上下游水位、消能效果显著等特点,成为应用最广泛和最有效的鱼道型式之一[6]。
研究发现,我国已建的竖缝式鱼道大多底坡较缓,为1/100~1/50[7]。而底坡坡度决定了鱼道的总长度,是影响鱼类上溯时间、工程建设成本及规划布置的主要因素。一般来说,鱼道底坡越陡,总长度越短,占地面积就越小,建设成本也越低。但是大底坡结构所形成的高速度、高湍动水流流场不利于游泳能力较弱的鱼类洄游上溯[8]。因此,考虑河流生态修复及工程经济性,国内外学者针对大底坡下竖缝式鱼道的水力优化开展了相关研究,如部分学者基于物理模型试验[9-10]和数值模拟[11-14]方法,分别研究了在各种大底坡(1/20~1/7)结构下,竖缝式鱼道竖缝下游处设置不同直径、个数及排列方式的圆柱体障碍物对池室水力特性的影响,并通过比较池室流速和池室湍动特性等相关参数来评估不同圆柱体配置方式的阻流效果。此外,也有部分学者研究了在竖缝处增设隔板对池室水流分布的影响,如Pena等[15]认为在底坡为1/10的竖缝式鱼道竖缝底部设置不同长度的隔板可以减小池室最大流速,但同时会产生比较复杂的流场结构并增加池室湍动能;Mallen-Cooper等[16]基于原型观测研究了底坡为1/20时在竖缝式鱼道竖缝中间位置设置隔板对鱼道过鱼效率的影响,发现与未经改造的竖缝式鱼道相比,其小鱼通过效率提升了6~13倍,这种通过在竖缝式鱼道结构水流最集中的部位设置消能措施以减少池室流速和湍流的方法比较有效、简单和经济,但是鲜见其相关的池室水力特性研究报道,而水力特征分布是探讨鱼类上溯行为机理的依据,也亟须对其进行相关研究。
综上所述,通过在竖缝式鱼道结构内增设局部消能措施(如圆柱体、竖缝隔板等)可改变池室流场分布,并且关于不同配置方式的圆柱体对池室水力特性的影响已进行了一定的研究,然而对于竖缝隔板所产生的影响,目前相关研究尚不够全面、系统,还有待进一步探索与分析。因此,本文从水力、工程经济等角度出发,在Mallen-Cooper等[16]的研究基础上,通过建立鱼道池室三维水动力数值模型,深入分析了5种大底坡J(1/40、1/30、1/20、1/15、1/10)条件下,竖缝隔板及其不同安装高度h(0、0.04、0.08m,为竖缝隔板底部到池室底板的距离)对池室水力特性的影响,并阐明了竖缝隔板影响和优化大底坡鱼道池室流场分布的内在原因。通过对池室水力特性的数值模拟研究,以期获取关于这类鱼道结构运行的基本知识,可为改进更有效、经济的大底坡鱼道结构提供相关技术依据。
1 数学模型
1.1 控制方程
本研究采用计算流体力学商业软件FlOW-3D对竖缝式鱼道内的水动力进行模拟,采用有限体积法求解三维雷诺平均纳维-斯托克斯(RANS)方程。湍流模型选用重整化群(RNG)k-ε模型,该模型能够较准确地模拟复杂水工结构内的流场分布[17]。
采用流体体积(VOF)方法模拟自由液面,即气相和液相之间的界面。VOF方法通过求解整个计算域内各网格单元的体积分数,并进行持续记录,构建出自由液面。其表达式为
(1)
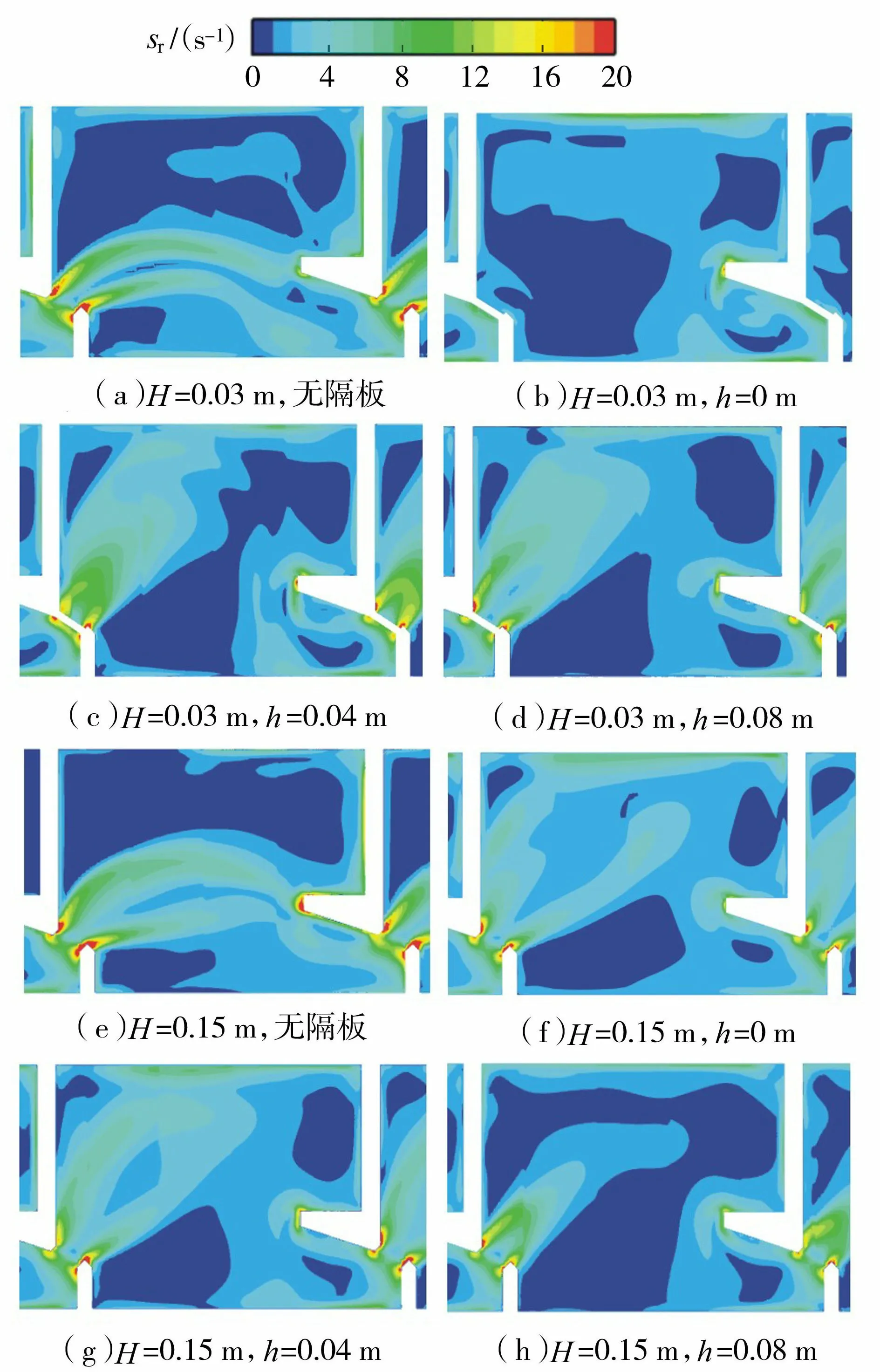
式中:aw为水的体积分数;t为时间;ui为流体速度;xi为坐标。当aw=0时,计算域内全部充满空气;当aw=1时,计算域内全部充满水;当0 数学模型计算域包括鱼道入流段、出流段及5级池室,如图1所示。竖缝宽度b为0.05m,单个池室净长L=10b=0.5m,净宽B=8b=0.4m,池室长宽比为10/8,底坡J分别取1/40、1/30、1/20、1/15、1/10。竖缝隔板尺寸为0.05m×0.01m×0.05m(长×宽×高),其中高度与竖缝宽度相等,布置方式如图2所示。为减少进出口边界对池室流场的影响,取第三级池室作为主要研究对象,采用六面体结构化网格对模型进行网格划分,网格单元边长设为0.006m。 图1 鱼道数学模型平面示意图 图2 竖缝隔板布置三维示意图 考虑到水流流动的物理特性及工程模拟的相似性,鱼道上游进口及下游出口边界条件均采用压力边界,并设置相应的水深,鱼道进口水深为0.195m,出口水深为0.245m;模型顶部设置为压力进口边界,其相对压强大小为0,水体体积分数设置为0,以便空气可自由进入;鱼道左右边墙及底部设置为固壁无滑移边界。模型初始水深H设置为0.2m,以使计算更快收敛并更加符合实际情况。模型采用广义最小残量(GMRES)隐式求解器计算,初始时间步长设置为0.001s,最小时间步长设置为10-7s。 为了评估数学模型模拟鱼道池室水动力特性的能力,通过调整数学模型中鱼道边墙及底部的表面粗糙度rs(0.010、0.012、0.015、0.018),采用与数学模型尺寸相一致的物理模型对各表面粗糙度下的流速进行了对比验证。物理模型试验在长沙理工大学水利实验中心的变坡水槽中进行,水槽尺寸为16m×0.4m×0.5m(长×宽×高),水槽底面及两侧均为透明的钢化玻璃。为得到充分发展的水流,将模型布置在水槽中后段部分,并通过多普勒声学流速仪测量了第三级池室z=0.5H水深平面处的速度场分布,池室流速测点布置如图3所示。对比分析了底坡为1/20且无竖缝隔板情况下,距上游长挡板背水面距离0.22m断面线处的物理模型与数学模型流速分布(图4(a))及不同水深竖缝断面中心点连线处的流速分布(图4(b)),并通过决定系数R2对数学模型计算精度进行评价。验证结果表明,当rs=0.015时,数学模型结果与物理模型结果吻合较好,R2都在0.9以上,数学模型能够较准确地模拟鱼道池室内的水力特性。 图3 第三级池室测点布置(单位:m) 根据上述数学模型,分别对各工况进行了模拟计算,为减少鱼道进出口边界条件对计算结果的影响,以中间第三级池室作为主要研究对象进行水力分析与讨论。 在竖缝式鱼道的水力设计中,池室最大流速vmax和池室湍动能k是影响过鱼效果最主要的水力参数[18]。由于竖缝式鱼道在相邻池室间会产生水位落差,vmax一般出现在竖缝位置附近,而竖缝是鱼类进行洄游的必经之地,因此,为使鱼类能够顺利通行,vmax必须小于鱼的爆发速度[19]。k表示脉动流速的动能,是衡量水流湍动程度的重要指标[20];若鱼类上溯路径中的水流k过大,会导致鱼类特别是游泳能力较弱的鱼类在上溯过程中难以保持方向,同时增加鱼类游泳耗能甚至对鱼类造成不同程度的伤害[21],这表明池室中适当的k分布也是鱼类成功上溯的关键。因此,优化大底坡鱼道池室水力分布的主要目标是减小池室最大流速和池室湍流。 表1 不同底坡最大流速和平均湍动能下降率 为了进一步阐明竖缝隔板对鱼道池室流场分布的影响机理,选取第三级池室距底板0.03m(竖缝隔板下方水深处,除h=0m时)及0.15m(竖缝隔板上方水深处)的水平面作为主要研究对象,具体分析了底坡为1/20时,不同竖缝隔板配置方式在Q=19.36m3/h和Q=10.23m3/h(Q为鱼道入口流量)下的池室水力特性分布。 2.2.1流态 图5为不同流量条件下竖缝隔板不同配置方式的三维流线分布:当竖缝处无隔板时(图5(a)(e)),水流通过上游竖缝后,以射流的形式进入池室,并沿池室隔板导角方向向前流动,射流到达池室中心后受下游挡板墩头影响,其断面逐渐收缩并同时折向下游竖缝进入下一级池室,呈现出反S形的主流,并在主流两侧产生了两个尺度相当的回流区;而对于大底坡和流量较大的情况,这种流型的主流流速(0.5~0.6m/s)过大,会导致鱼类上溯耗能的增加并不利于游泳能力较弱的鱼类通行。竖缝处设置隔板后(图6(b)(c)(d)(f)(g)(h)),水流也以射流形式流入池室,但整体流动模式发生了显著变化:竖缝隔板的存在改变了射流流向,形成了利用池室整体容积进行低湍流能量转换、自身回转的主流,使得主流路径更加弯曲并呈Ω形,该流型通过射流混合消能的方式,可有效延长大底坡、大流量条件下的水流能量耗散距离,在池室内形成面积较大的低流速区(0.25~0.35m/s),使鱼类能以持续游泳速度和耐久游泳速度相交替的游泳方式[22]游过各级鱼道池室,有利于减小鱼类上溯耗能;同时,在池室的上游角和主流的凸出部分产生了两个尺度不一的回流区,给鱼类洄游提供休息区域。而改变竖缝隔板安装高度,流态呈现相似的分布规律。 图6 不同水深处池室流速分布 图6为Q=19.36m3/h时竖缝隔板不同安装情况下不同水深处的池室流速分布。与无隔板相比,3种隔板安装高度下的池室流速都显著下降,且具有相似的分布情况;当h为0时,在0.03m水深处(图6(b)),由于竖缝隔板的阻挡,其竖缝下游处的流速分布较缓;而竖缝隔板上下水深处的流速分布(图6(c)(d)(f)(g)(h))大体保持一致,这表明改变竖缝隔板安装高度,对其上下水深处的流速分布无显著影响。 2.2.2主流区水力特性 图7 最大流速轨迹线 图8 最大流速沿程分布曲线 2.2.3竖缝断面流速 分析发现,不同流量条件下竖缝断面流速分布规律具有较好的相似性。因此,图9仅给出了Q=19.36m3/h时H=0.03m和H=0.15m处竖缝断面流速沿竖缝宽度b方向的分布规律。在竖缝处设置隔板使竖缝中间位置(b′/b=0.3~0.9,其中b′为竖缝上的点到隔板的距离)的流速显著下降,而对靠近两侧挡板处的流速影响较小;同时,当h=0m时,鱼道底部由于竖缝隔板的阻挡,使得鱼道底部(H=0.03m)竖缝流速为0,因此图9(a)未给出其流速分布,当h=0.04m时,对竖缝隔板上方水深处(H=0.15m)的流速影响较小,当h=0.08m时,竖缝隔板上下水深处(H=0.03m、0.15m)的流速都有明显降低,这表明竖缝隔板能显著减小其安装位置附近水深处的竖缝断面流速,且h越大,这种影响范围也越大。基于此,初步认为可将隔板安装在竖缝的中上方水深处,以保障鱼类能够更加顺利地通过竖缝完成洄游。 图9 不同水深处竖缝断面流速分布 2.2.4湍动能 图10为Q=19.36m3/h时竖缝隔板不同安装情况在不同水深处的池室湍动能分布:不同工况池室湍动能的分布与其所对应的池室流型分布具有较好的一致性;在不同水深处(除竖缝隔板阻挡水深处),湍动能最大值均出现在竖缝附近,同时水流通过竖缝后由于主流区流速较大,两侧回流区流速较小,造成主流边界流速梯度较大,因此在主流及其左右边界的剪切区域亦表现出较大的湍动能,并随着水深的增加,池室中湍动能的分布规律大致相同,但相同位置的湍动能有所增大;与无隔板相比,竖缝处设置隔板可降低池室湍动能的大小,并使其在竖缝下游位置区域内迅速衰减,产生连续的低湍动区域(0.007~0.01J/kg),这给鱼类特别是游泳能力较弱的鱼类提供了一个较好的上溯条件;同流速分布一样,改变竖缝隔板安装高度,对竖缝隔板上下水深处池室湍动能的分布规律无显著影响。 图10 不同水深处池室湍动能分布 2.2.5应变率 应变率(sr)为水流各方向速度梯度的绝对值之和。相关研究[24-25]认为水流速度梯度的大小是影响鱼类侧线系统感知水流刺激并产生运动的重要因素,因此,应变率也是研究鱼道水力特性的重要参数之一。图11为Q=19.36m3/h时不同隔板安装情况下不同水深处的池室应变率分布。与池室湍动能分布一样,应变率分布也取决于池室流型的分布,并沿主流两侧边界有逐渐减小的趋势;同时在竖缝位置内侧以及靠近竖缝处下游位置的两侧呈现相对较大的数值,即在这些区域水流速度变化显著、流速梯度大(竖缝隔板阻挡水深处除外);设置竖缝隔板会使应变率的分布在竖缝下游处发生偏转,但对应变率的大小没有显著影响,这表明鱼类能在小流速和低湍动的水流条件下感知到相同的水流刺激向前运动,可促进鱼类的洄游上溯;而改变竖缝隔板的安装高度,对竖缝隔板上下水深处应变率的分布规律无明显影响。 图11 不同水深处池室水力应变率分布 a.对于不同的大底坡坡度,竖缝处设置隔板可有效减小池室最大流速及池室平均湍动能:池室最大流速下降率分布范围为2.01%~21.49%,池室平均湍动能下降率分布范围为3.77%~42.19%。 b.底坡为1/20时,池室主流从反S形转变为利用池室整体容积进行低湍流能量转换并自身回转的Ω形,并且其主流最大流速衰减率达到61.24%~61.82%。 c.改变竖缝隔板安装高度对隔板上下水深处的竖缝流速分布存在一定的影响,而对流速、湍动能、水力应变率的分布规律无显著影响,因此为了使鱼类能够更加顺利地通过竖缝,可将竖缝隔板安装在竖缝的中上方水深位置。 d.在竖缝处设置隔板以优化大底坡鱼道形成的高流速、高湍动的水流流场具有一定的可行性,但是还需进一步结合过鱼试验研究来评估鱼类对这些水动力条件的上溯行为反应,以论证研究结果的工程应用价值。1.2 计算域及网格划分
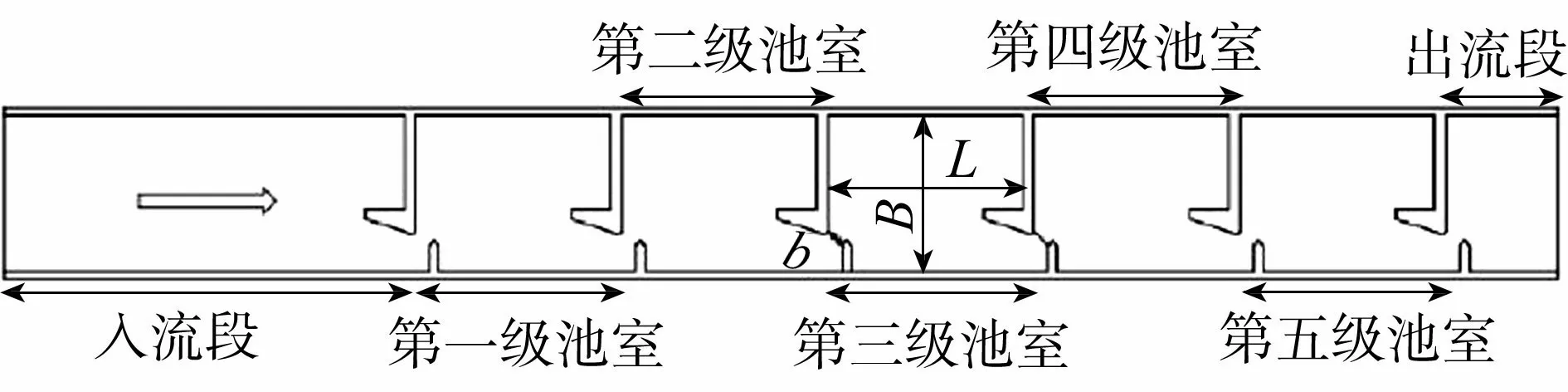
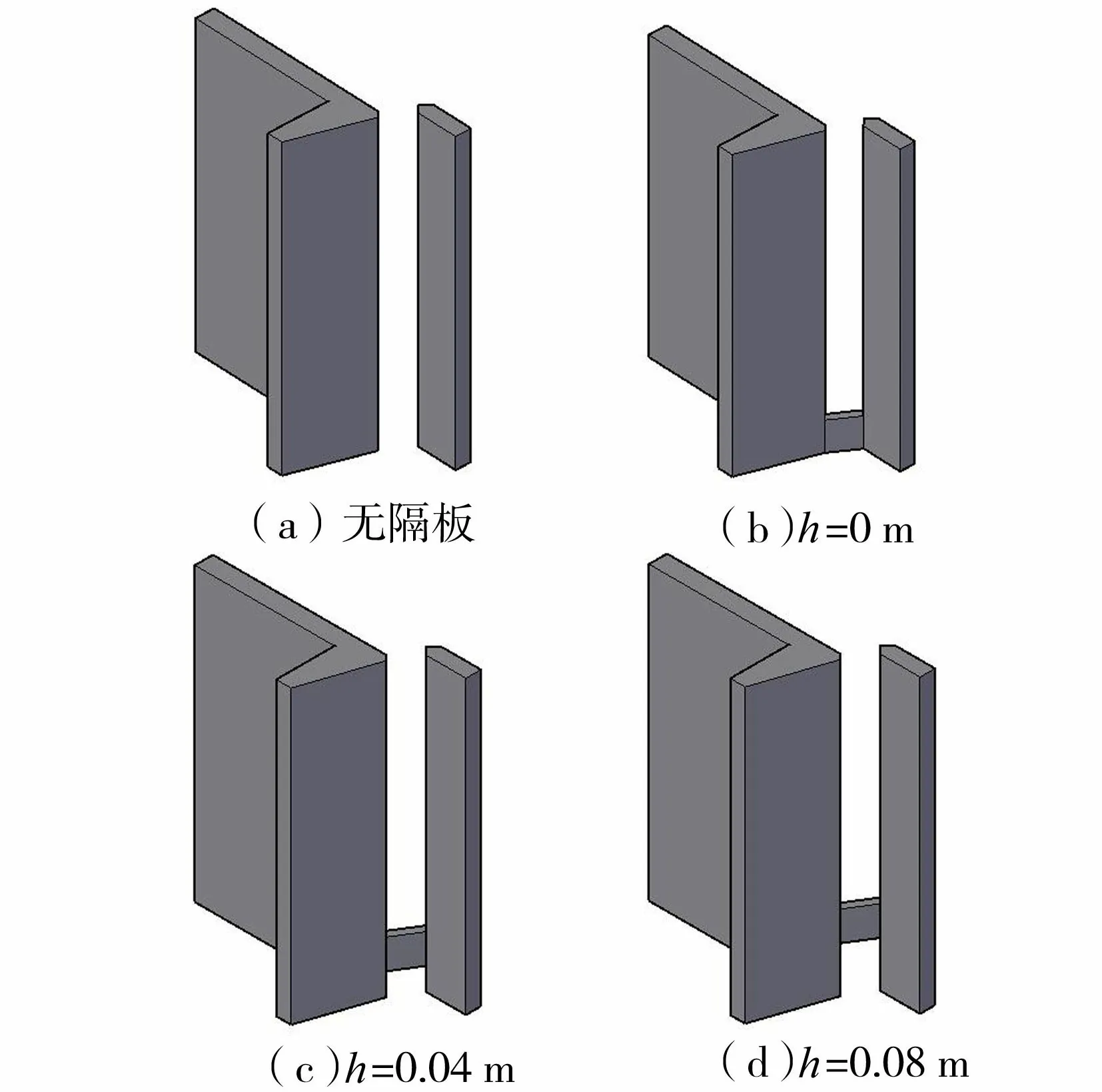
1.3 边界条件及初始条件
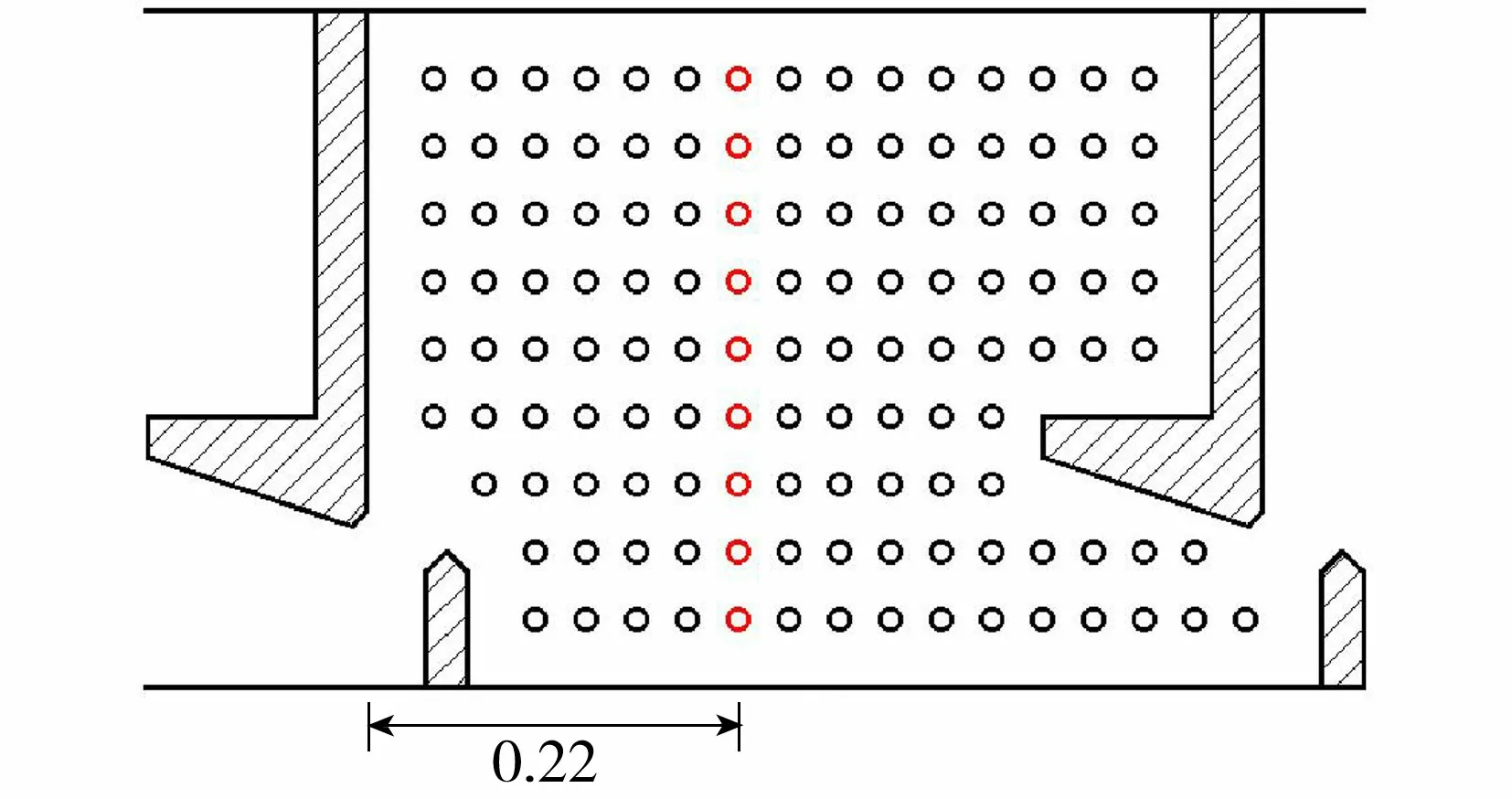
1.4 数值模拟与物理模型试验结果对比分析
2 结果与分析
2.1 不同底坡池室水力参数对比
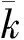

2.2 竖缝隔板对池室水力特性的影响

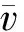

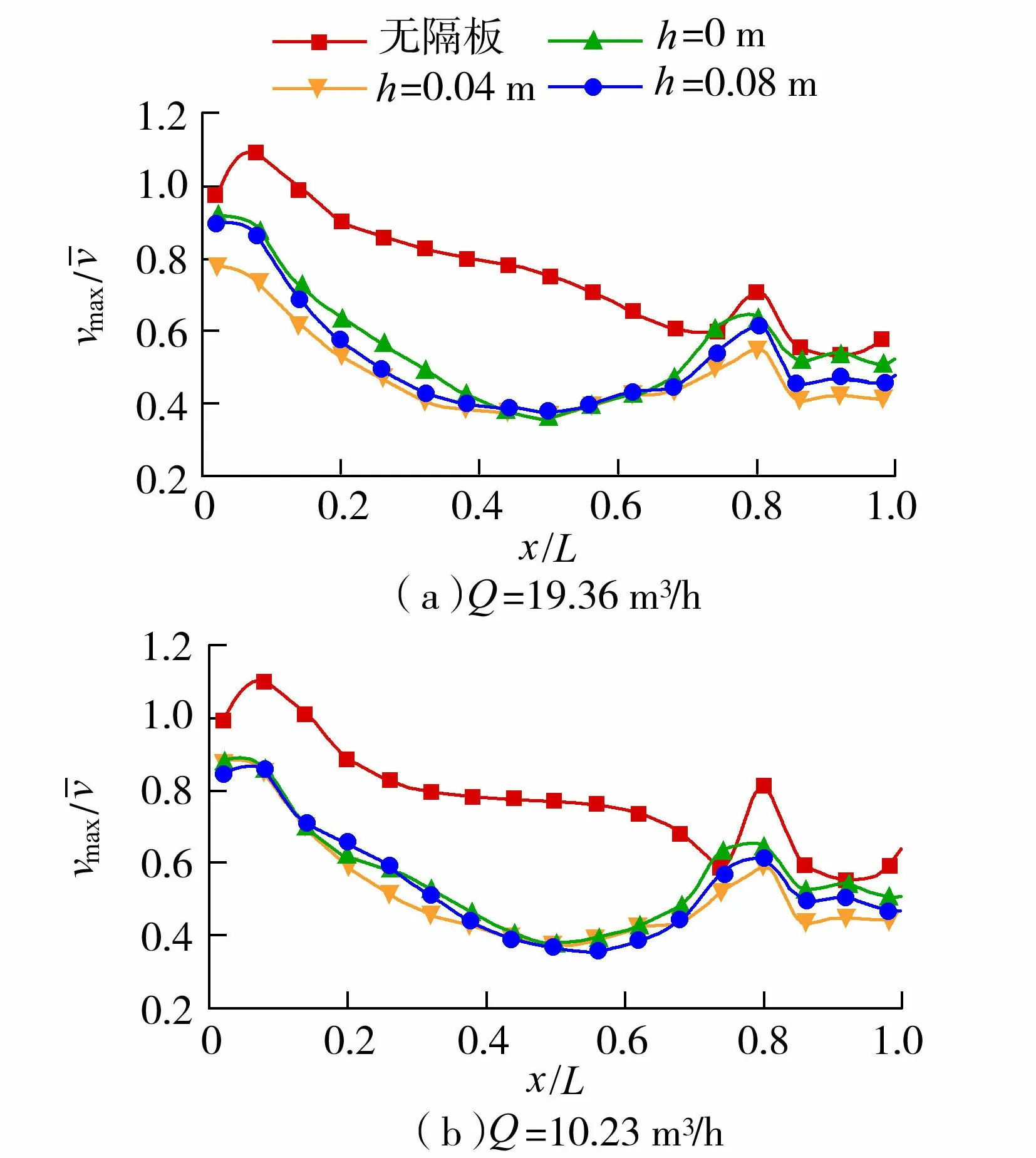
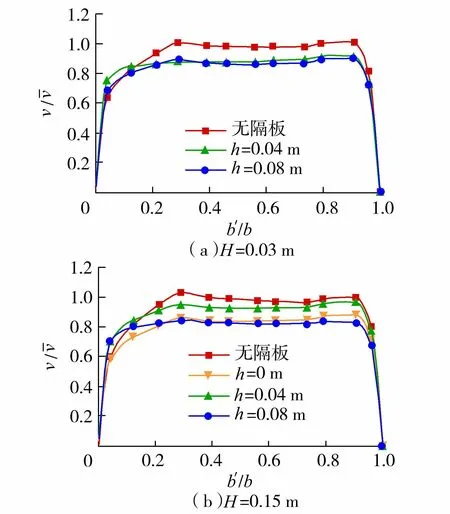
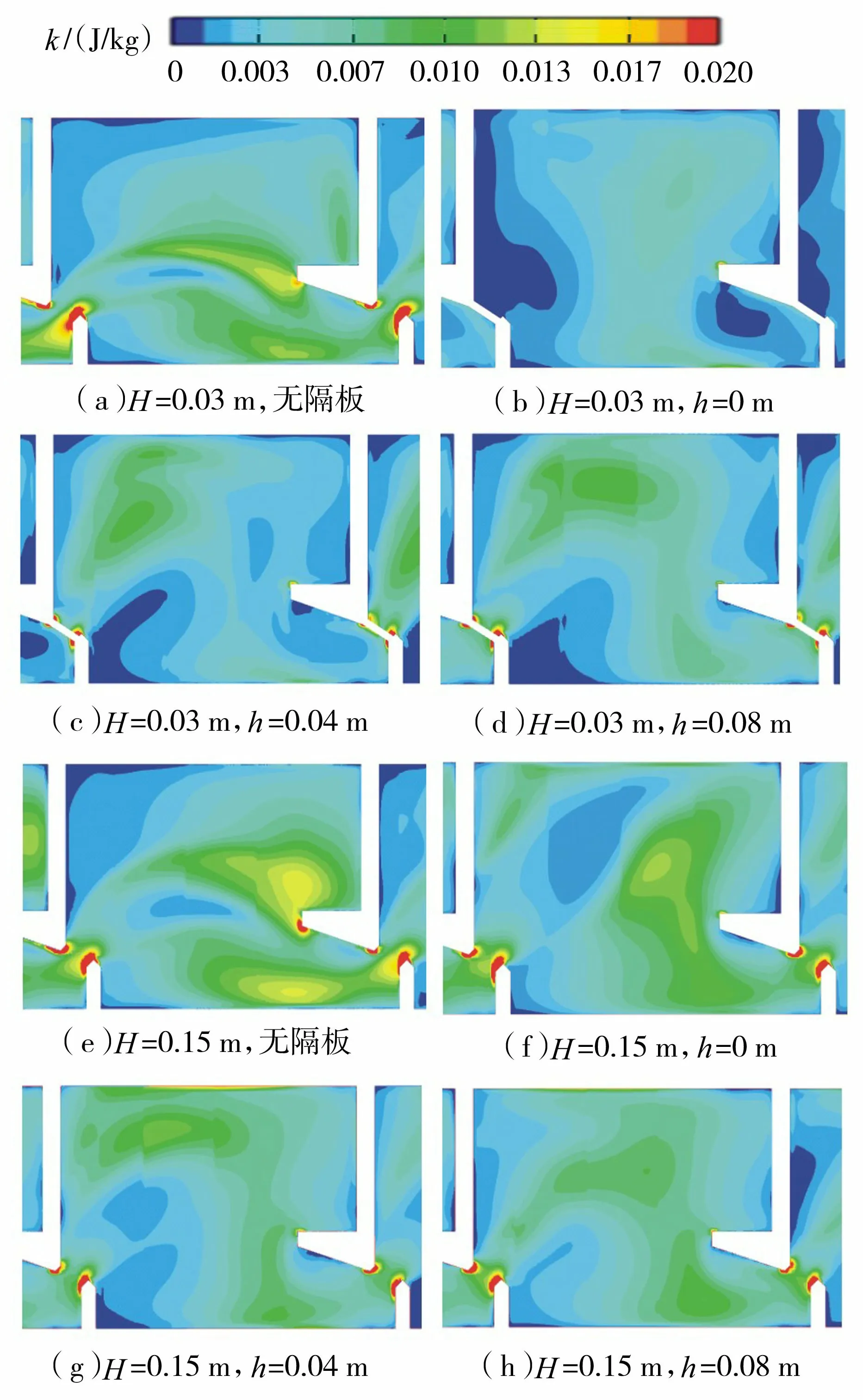
3 结 论

