跌流竖井结构优化及其气压特性数值模拟

芦三强,乔时雨

(1.兰州理工大学能源与动力工程学院,甘肃 兰州 730050; 2.河海大学水文水资源学院,江苏 南京 210098)

跌流竖井作为水利工程及市政排水系统中广泛使用的输水建筑物之一,主要用于将上游海拔较高处管道中的水流转移到下游海拔较低的排水管道中[1-2]。不同于旋流竖井[3]、折板竖井[4]等其他类型竖井的进水方式,跌流竖井中水流从进水管处以水舌的形式直接自由跌落,水舌撞击井壁后会在进水管附近形成一个水体阻隔区域,造成竖井内通气不畅、负压过大以及卷吸气量过多等问题[5-8]。

跌流竖井内负压过大会引发一系列问题,如排污管道中气体流通的空间被加压,会导致排污系统中产生的一些臭气从一些地表开口逸散到外界环境中[9-10];在极端暴雨天气下还可能会引发井喷,冲起的井盖在下落时可能会砸伤行人和引发交通事故等[11-12]。为了降低水舌引起的负压过大问题,芦三强等[13]在跌流竖井进水管附近布置了一个有旋分流隔板,目的是改变下落水流的流动方向,使水流围绕隔板两侧旋转流动,同时隔板中间形成了一个不过水的空腔区域,能有效防止水舌束窄气体流通的空间。龚旭[14]在进水管与立管交汇处上方放置了一个挡板,其目的是调节进水管中跌落水舌的入流角度,使水舌直接撞击到挡板上而不是管壁上,从而在进水管附近保留一定气体流通空间。以上关于跌流竖井进水管附近的结构优化设计都发生在竖井结构内部,尽管能起到一定的通气和调节气压的作用,但是由于占据了部分水体流通的空间,影响了竖井的过流能力,同时也不利于后续检修作业等。

本文基于文献[7]中的竖井几何模型(原始竖井模型),采用数值模拟的方法研究了原始竖井模型进水管附近的流态与气压分布规律,分析了进水管附近负压突增的原因,提出了改善进水管附近通气状况的结构优化方案,建立了可以确定通气管道安装高程的理论模型,并评估了优化竖井模型的性能,最后探讨了通气管道相对进水管的位置对优化竖井模型内气压分布的影响。

1 竖井模型数值模拟

1.1 数值模型

1.2 几何模型及网格划分

优化竖井模型几何结构如图1(a)所示,该结构以竖井顶部中心为原点,z轴向下为正方向进行建模。优化模型由原始竖井模型与添加在进水管正对面的通气管道组成,通气管道主要作为水舌阻隔区域气体流通的通道。通气管道主要包括水平管、竖直管和倾斜管,其直径均为0.1m,水平管的长度为0.36m,竖直管的高度为0.85m,倾斜管与竖井井身的夹角为70°,设置倾斜管的目的主要是防止贴壁水流发生回流,堵塞通气管道的出口,原始竖井模型的几何参数可参见文献[7]。

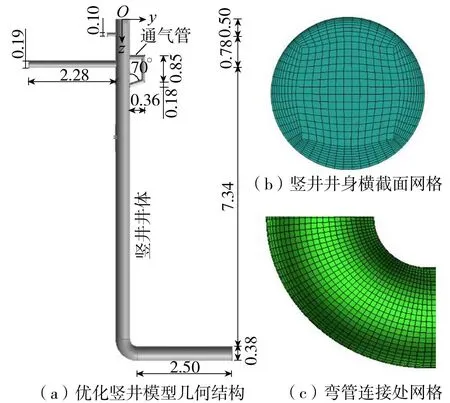
图1 优化竖井模型几何结构和网格划分(单位:m)

利用ICEM CFD软件进行网格划分。考虑到竖井结构为规则的圆柱体结构,采用O-grid方法能够很好地将计算域划分为六面体结构化网格,同时也便于生成边界层网格。可实现的k-ε湍流模型适用于雷诺数较大的湍流核心区域,而对于雷诺数较小的近壁面区域则配合壁面函数法进行求解,本文选用非平衡壁面函数法进行处理。将边界层网格的层数设置为15层,第一层网格高度设为0.6mm,每层按照指数方式增长,增长率为1.2,划分完的网格如图1(b)和(c)所示。

1.3 边界条件及工况

1.4 网格无关性验证

为了验证网格数量对计算结果精度的影响,对23万、36万、47万和65万共4种不同数量的网格在Fluent中采用相同的设置进行计算求解,选取无量纲入流量为0.07的工况进行网格无关性检验并观察竖井内的垂向气压变化,结果如图2所示。由图2可知,随着网格数量的增加,计算结果的精度的确在提高,但是当网格数量增加到47万和65万时,计算结果趋于稳定并不再变化,并且47万和65万网格下监测到的压力曲线与测量值吻合较好,也说明了数值模拟结果的准确性,因此选择47万网格进行后续的模拟。

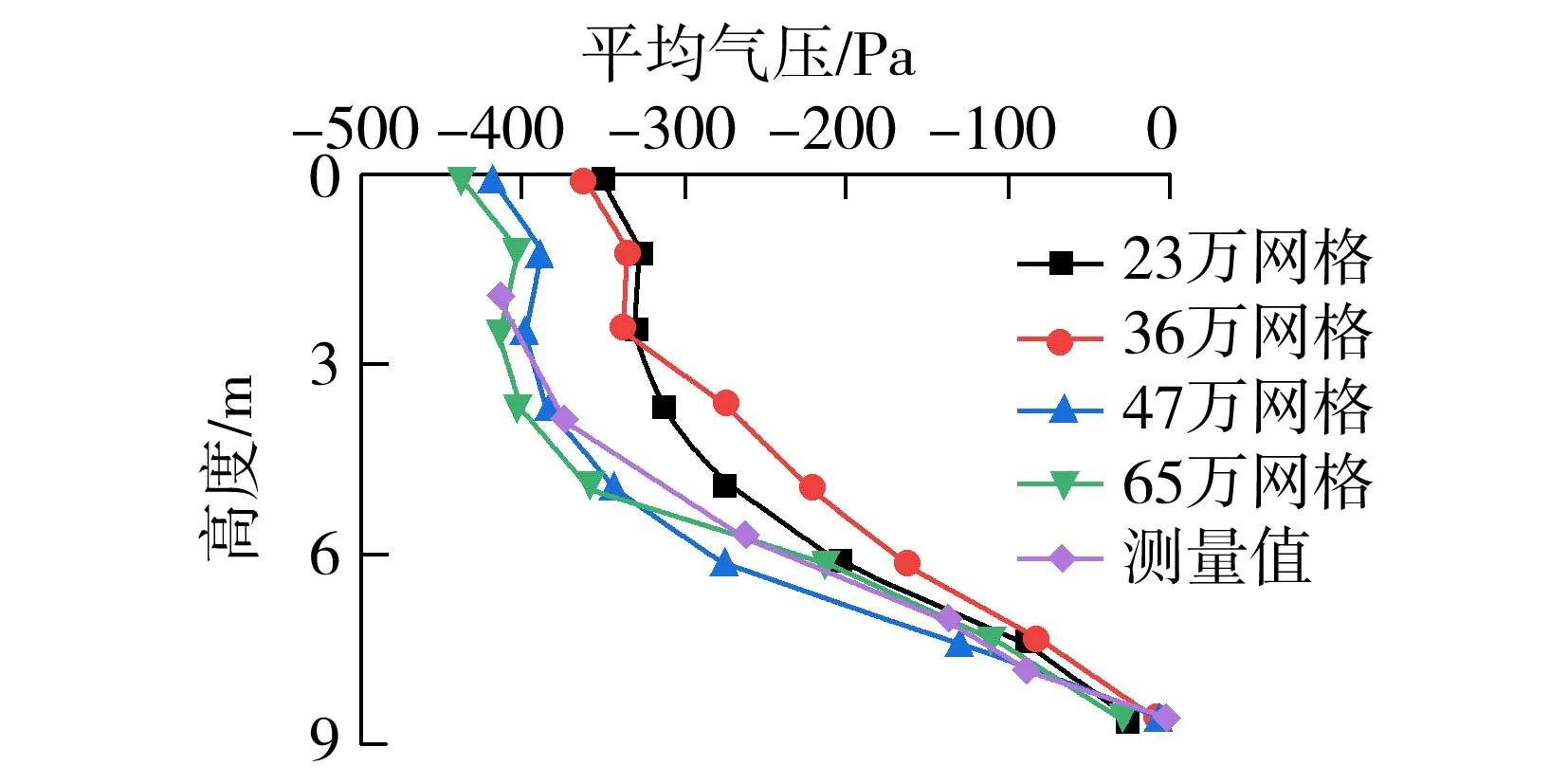
图2 网格无关性验证

2 结果与分析

2.1 数值模拟准确性验证

为了验证数值模拟结果的准确性,利用不同入流量下进气管中气体流速的模拟值与文献[7]中利用气压测量值计算出的流速值进行比较,结果如图3所示。由图3可见,不同入流量下进气管中气体平均流速的模拟值与测量值吻合良好,最大误差不超过6%,说明数值模拟的结果是可靠的。

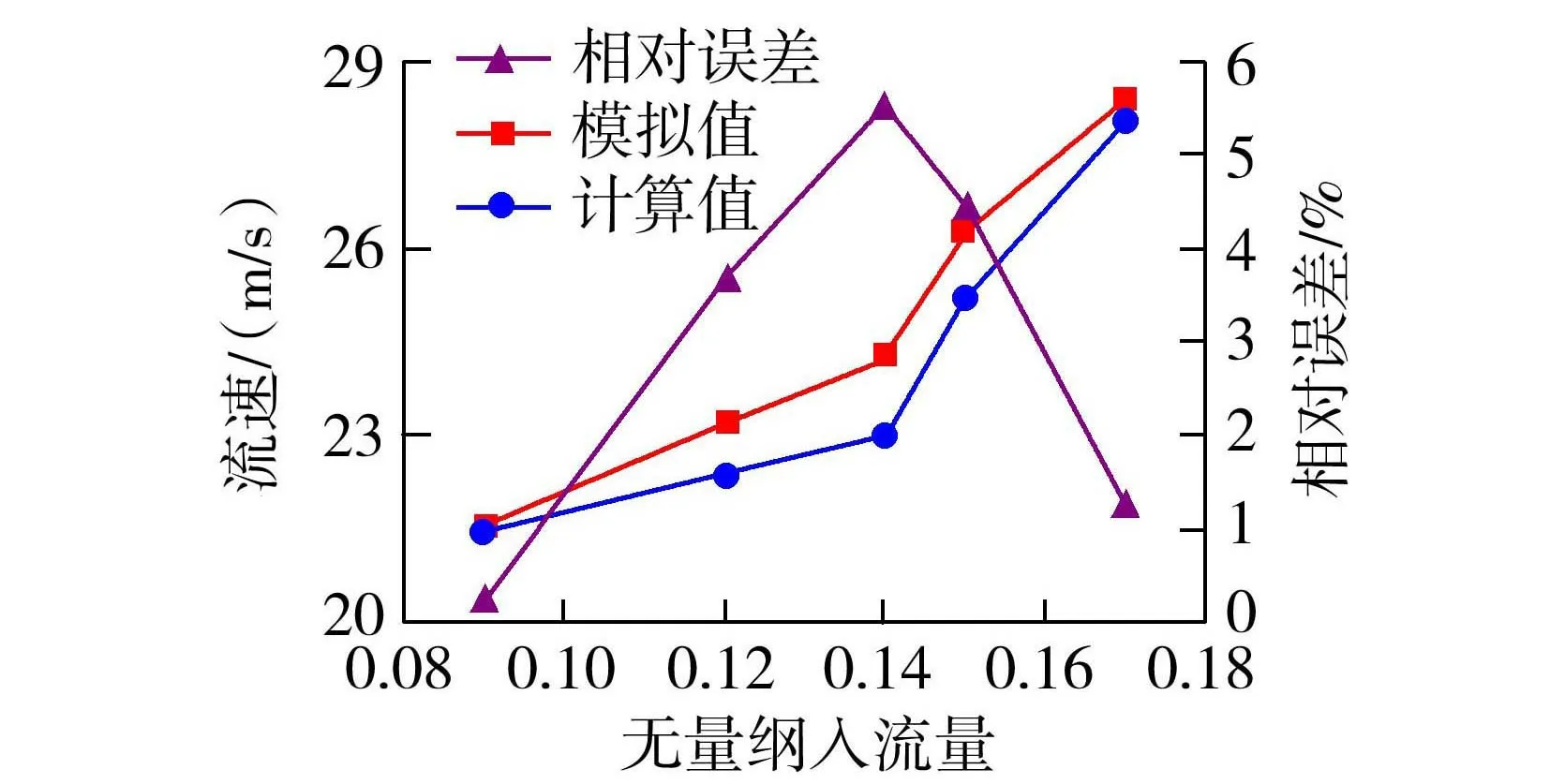
图3 进气管气体平均流速对比

2.2 井身横向压强分布

为了探究入流水舌对进水管附近井身横截面上压强分布的影响,以无量纲入流量0.09和0.12为例,在z=1m(水舌影响区域上端)、z=1.5m(水舌影响区域)和z=2.5m(水舌影响区域下端)处共选取3个截面进行分析,结果如图4所示。当无量纲入流量为0.09时,由图4(a)可见,在z=1m截面上,最大压差约为3Pa,说明在水舌上端区域,整个截面上的气压变化很小,基本上是均匀分布的;由图4(b)可见,整个截面上(z=1.5m)的压强也基本相同,只有进水管正对面有一小部分区域表现为正压,这是由于水舌撞击到对面的井壁上造成的;由图4(c)可见,除了井壁以及进水管正对面位置处有压力的升降外,其他区域的压强也是均匀分布的,这是因为水舌撞击到井壁后,会有部分水流贴着壁面下落,因此壁面位置处压力会比竖井中央大。当无量纲入流量为0.12时,3个位置处竖井截面上的压强分布与无量纲入流量为0.09时的情况相似。综上所述,同一入流量下,除了有水舌撞击的区域以及井壁上有水流附着的区域外,同一平面上的横向压强是均匀分布的。

图4 竖井井身横截面上的压强分布

2.3 垂向气压分布

原始竖井模型内的垂向气压分布如图5所示。由图5可知,竖井内相同位置上的气压(负压)随着入流量的增大而增大;同一流量下,从竖井顶部到底部气压整体呈现不断增大的趋势,说明竖井内气体卷吸现象严重,竖井底部被不断加压。由图5还可以看到,在z1(z=1.23m)～z2(z=1.85m)区域内负压表现为突然增大,并且z2处为竖井内负压最大的地方,同时入流量越大,z1～z2区域内的垂向气压梯度也越大,如当无量纲入流量为0.09、0.12、0.15、0.17时,z1和z2两者间压差的绝对值分别为14.67、43.99、104、161Pa,增幅很大。从进水管附近的流速分布规律可知,z1～z2区域的负压之所以会突增,主要是因为水舌束窄了该区域内气体流通的通道,导致气体在该区域发生了大面积回流,水舌下方补气不足。

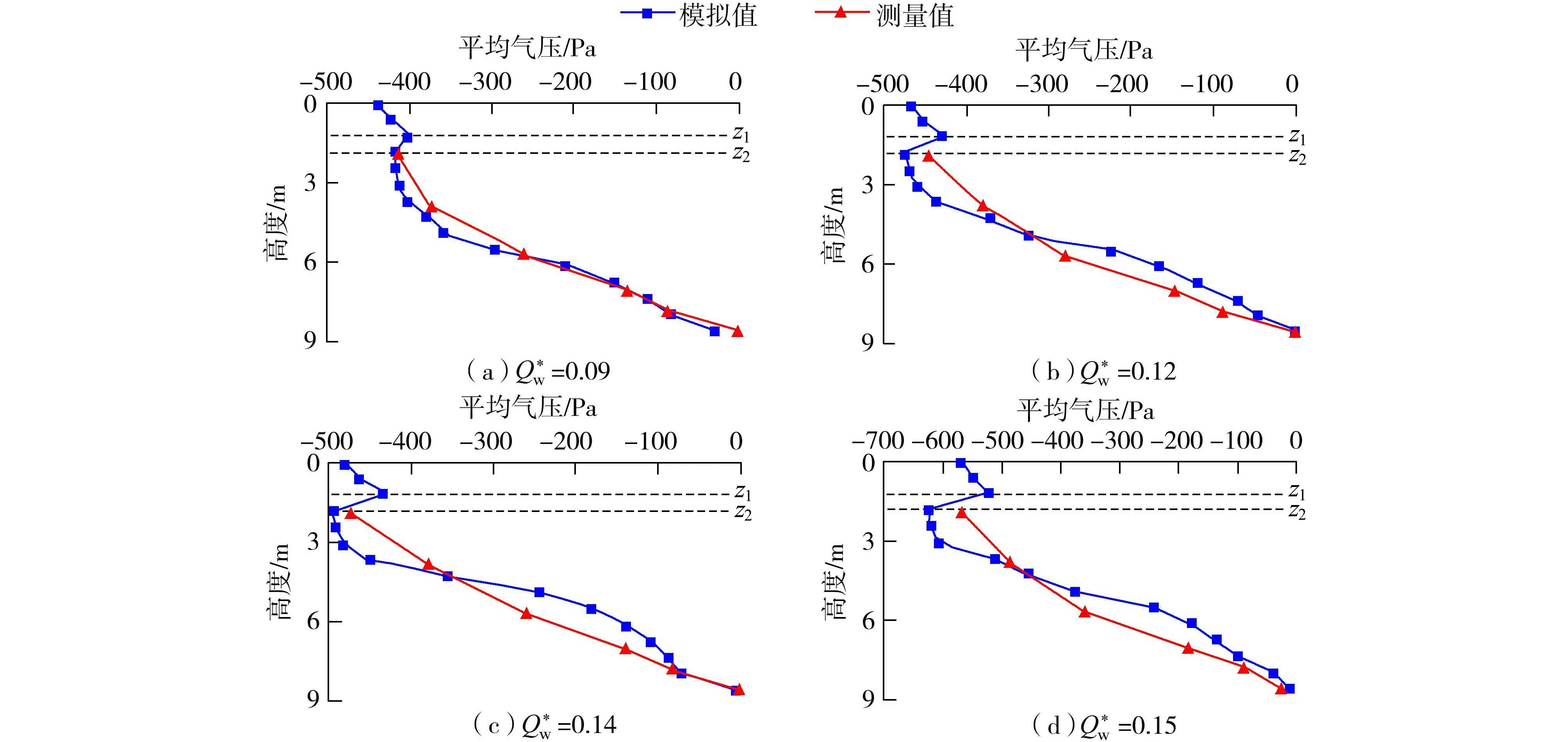
图5 原始竖井模型内垂向气压分布

2.4 进水管附近流速矢量和流线分布规律

本文重点探讨进水管附近的水舌运动及其影响,图6为进水管附近流速矢量与流线的分布。由图6可知,进气管中的气体进入竖井后先是与井壁相撞,一部分气体沿着井壁向上运动并在进气管上方形成了回流区,另一部分气体向下运动并在进水管附近受到了水舌的阻挡,在与水舌发生碰撞后,开始反向流动,在进水管与进气管之间形成了一个较大的回流区。不同的是,图6(b)中在水舌与井壁碰撞出又形成了一个回流区,这主要是由于随着入流量的增大,水舌与井壁撞击后形成的水体面积增大,导致该区域气体过流空间不足,所以气体发生了回流。而图6(a)中由于水舌所占据的空间还不足以影响气体的流动,所以并没有在该处形成回流区。

在操作练习时分小组进行，每个人分配不同的角色，进行不同的对话。团队练习能够使护生认识到一项操作的完成需要团队的合作，无形中培养了团队合作精神。

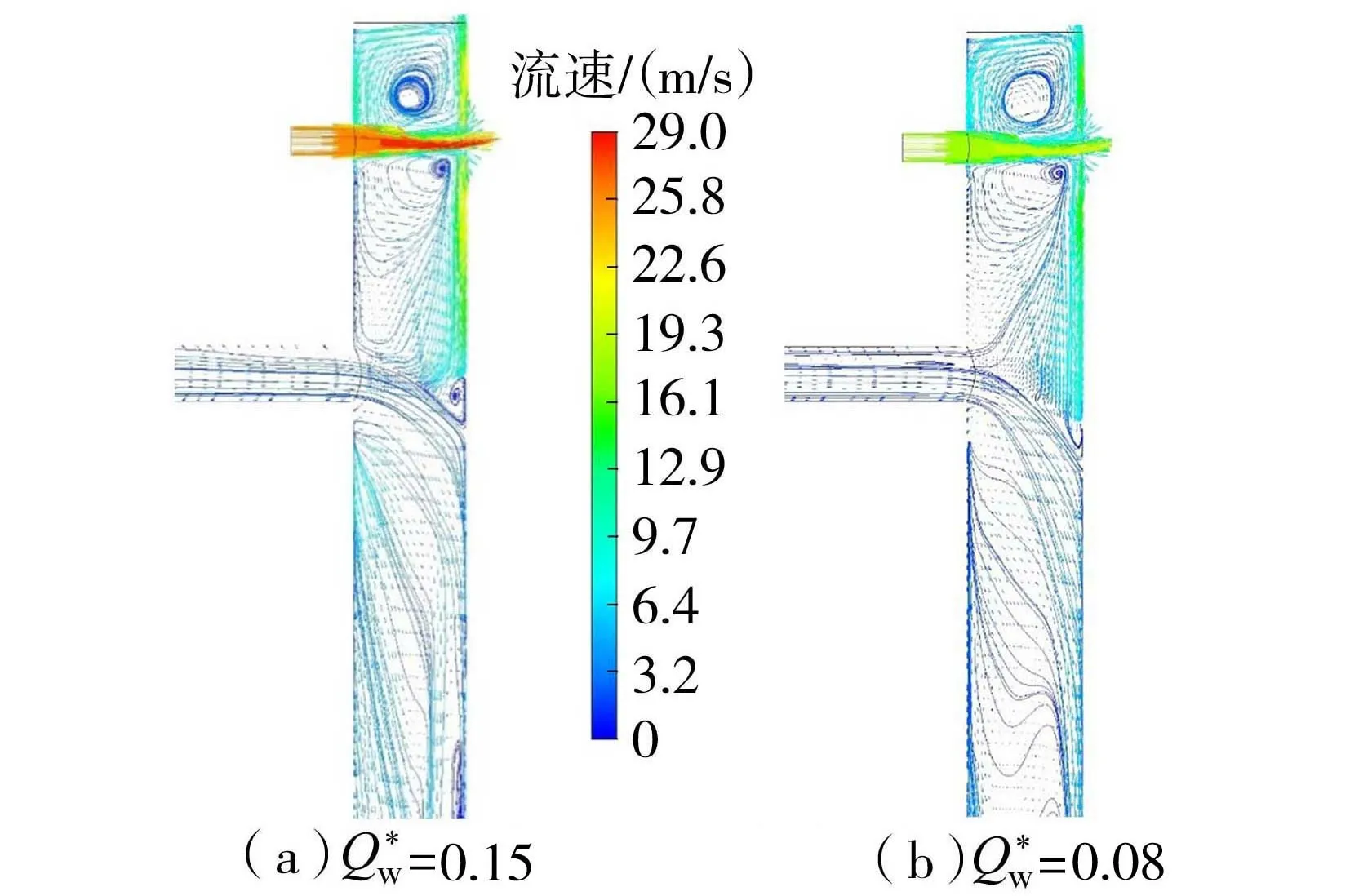
图6 进水管区域流速矢量与流线分布

3 跌流竖井的结构优化

3.1 通气管道安装高程的确定及气压对比分析

通气管道的主要作用是连通被水舌阻隔的气体流通通道,方便水舌阻隔区域通气,因此确定通气管道的安装高程和位置就需要确定水舌阻隔区域的大体位置,水舌阻隔区域即水舌从进水管下方跌落到撞击到对面井壁上的区域。基于这个目的,本文提出一种水舌撞击模型,该模型旨在预测水舌末端撞击点的位置(水舌下落的起点位置已知,即进水管末端高程),建模时将水舌的跌落过程近似地看作是一种类平抛运动。关于水舌末端撞击点高度的计算过程如下:

a.确定水舌做类平抛运动的水平速度v1。显然,v1就是进水管中水流的流速,即

v1=Qw/A

(1)

式中A为进水管中水流的横截面积。

b.确定水舌从进水管下落到撞击到井壁上所需的时间T:

T=x/v1

(2)

式中x为水舌做类平抛运动的水平位移。由于井壁的约束,水平位移最大为竖井的直径长。

c.确定水舌从起始点下落到撞击点C的垂直距离Y,即撞击点C的高度:

Y=gT2/2

(3)

(4)

式中DI为进水管的直径。

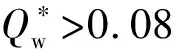
表1 水舌做类平抛运动时的计算参数

为了评价安装通气管道后优化竖井模型的性能,本文分析了4组无量纲入流量(0.09、0.12、0.15和0.17)下优化竖井模型内的气压分布情况,并与原始竖井模型进行了比较,结果如图7所示。由图7可以发现,相比原始竖井模型,优化竖井模型能够大幅降低竖井内的整体负压,进水管附近z1～z2区域基本上没有出现负压突增的情况,并且气压梯度也逐渐趋于平缓,基本上消除了水舌对进水管附近气压的影响。当无量纲入流量为0.09、0.12时,负压突增区z1和z2两者间的压差分别为1、3Pa,相比原始竖井中的14.67、43.99Pa,该区域的压差均降低了93.2%;无量纲入流量为0.15、0.17时,z1和z2两者间的压差为16、34Pa,相比原始竖井中的104、161Pa,分别降低了84.6%、78.9%。尽管随着流量的增大,通气管道发挥的作用有所降低,但是当进水管达到最大无量纲入流量0.17时压差仍能降低70%以上。从图中还可以发现,竖井中的负压整体有所减小,相比原始竖井结构,4组入流量下优化竖井中的上下游压差分别降低了54.8%、52.4%、57.1%和40.6%,平均降低约50%。

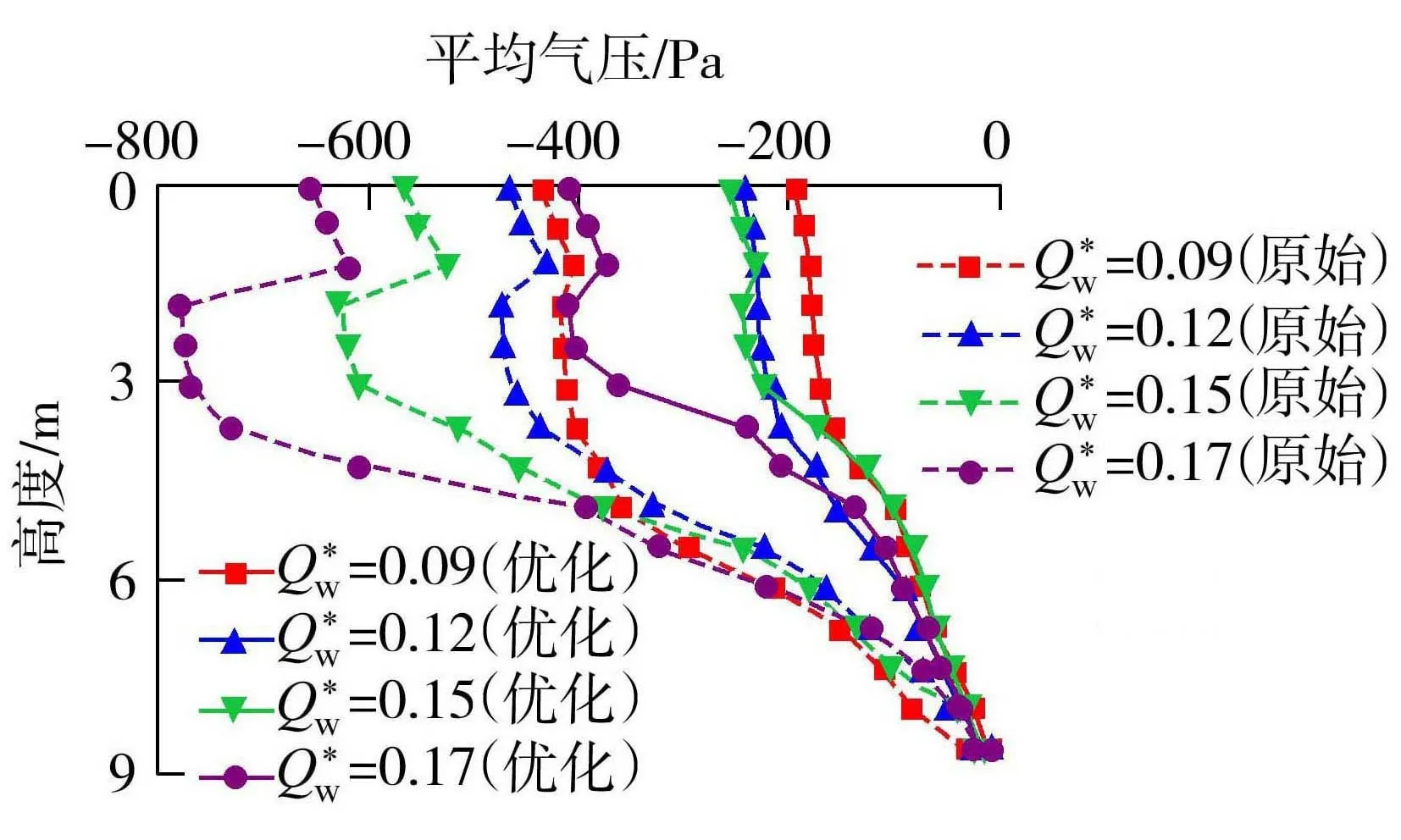
图7 优化竖井模型与原始竖井模型的气压分布对比

3.2 通气管道相对进水管的位置对气压分布的影响

优化模型通气管道是安装在进水管正对面的(见图1(a)),考虑到通气管道相对进水管的位置可能会影响通气管道的性能,本文对此进行了探讨,具体做法是将通气管道分别设置在与进水管水平中心延长线分别呈30°、60°和90°角的位置处(30°工况、60°工况、90°工况),具体结构如图8所示。

图8 通气管道与进水管的相对位置

图9为3种角度工况时优化模型中的气压分布(由于通气管道可以沿进水管水平中心线两侧对称布置,所以只探讨通气管道布置在进水管水平中心延长线一侧的情况)。由图9可知,通气管道相对进水管呈不同角度时,竖井内的气压分布有着较大的变化:①通气管道布置在进水管正对面(0°工况)时,相比其他位置的通气管道,此时竖井内的负压降低最少,也就是说,当通气管道布置在进水管正对面时其所发挥的效果最差;②而当进水管与通气管道垂直(90°工况)时,尽管竖井内的整体气压比0°工况效果要好,但是相比30°和60°工况仍要差;③30°和60°工况的气压分布曲线接近,但当流量开始增大时,30°工况更好。综上所述,30°工况最优,60°工况次之,90°工况较差,0°工况时最差。究其原因,主要与竖井内的水气两相分布规律有关,由于跌落水舌会撞击在进水管正对面并且会出现反弹,进水管延长线两侧会留有空隙,所以当通气管道与进水管延长线呈现一定夹角时竖井内更容易通气。

4 结 论

a.水舌对跌流竖井内的垂向气压分布影响很大,尤其是z1～z2区域,该区域的负压增长明显。水舌阻隔了进水管附近气体流通的通道是造成z1～z2区域负压突增的主要原因。

b.建立的水舌撞击模型能够较准确地预测水舌撞击井壁的位置,为通气管道的安装提供理论依据。

c.优化后的竖井结构能够有效降低竖井中的负压,并且使垂向气压梯度趋于平缓。相比原始竖井模型,优化竖井模型能够有效降低z1～z2区域的负压差约70%,平均降低竖井上下游压差50%左右。

d.通气管道与进水管的相对位置极大地影响了优化竖井模型的性能。当通气管道与进水管水平中心延长线之间呈现30°角时,优化竖井模型内的负压会大幅降低,并且z1～z2区域没有明显的负压突增现象。