三维挑流水舌及其碰撞的LBM数值模拟研究
彭燕祥,张 华,吴国华
(华北电力大学 水利与水电工程学院,北京 102206)
1 研究背景
随着中国水电事业的不断发展,水电站向高水头、大流量的方向发展。泄洪雾化问题越发突出,尤其是采用挑流消能方式泄洪时,会在水电站下游局部区域形成大面积的雨雾。相关的研究表明:挑流泄洪雾化与水舌自身掺气扩散、水舌之间相互碰撞和水舌入水喷溅密切相关,要对挑流泄洪雾化进行更深入的研究,就必须对挑流水舌的运动特性,以及水舌与空气的耦合作用引起的水舌风场进行研究。
针对水舌的运动特性,许多学者建立不同的数学模型进行了研究,刘宣烈等[1-3]通过实验对水舌运动过程的掺气和扩散过程进行研究,得到了水舌运动的轨迹方程以及水舌横、纵断面的扩散规律。梁在潮等[4]对水舌运动轨迹、水舌掺气量以及雾源量等参数进行了研究,并对这些参数进行拟合。张华等[5]通过建立水舌运动微分方程,并用数值方法进行求解,来研究空中水舌运动特性。刘士和等[6]运用相似理论在考虑空气阻力及卷吸掺气的作用下,建立了挑流水舌的数学模型。刘继广等[7]依据掺气浓度相似律准则进行气水两相流模拟研究。张贝贝等[8]提出一种在排放口近区考虑射流垂向效应、在全计算域使用二维平面模型的计算方法。但是这些研究仅仅是对水舌进行了研究,由水舌引起的水舌风场并没有涉及。
为了研究水舌与空气的耦合作用引起的水舌风场。李敏等[9]采用非静力闭合边界层模式,模拟了水电站泄洪条件下水舌风的发展过程。彭燕祥等[10]用CFD方法模拟了二滩水电站泄洪时水舌的运动及水舌风场的空间分布。彭莘仔等[11]采用N-S方程模拟射流的水动力过程。但是这些方法都是基于有限元网格的欧拉方法,这个方法对于流体运动的范围有其局限性,网格的划分密度以及范围都对误差的影响很大。
格子玻尔兹曼方法(Lattice Boltzmann Method,LBM)是一种介观流体系统模拟方法,兼具宏观流体连续性和微观分子动力学方法的优点,而且计算效率较高,现已被广泛应用于多组分多相流、化学反应流、气固两相流的研究[12-14]。在水汽两相流两方面,宋歌等[15]应用LBM方法对离心式雾化喷嘴出口处的液膜厚度、雾化锥角以及其他雾化特性进行了研究。叶永等[16]采用LBM对三维溃坝流进行了数值模拟与验证。两者都没有对空气流场进行研究。张华等[17]应用格子Boltzmann两相流模型,对水舌在空气中的运动进行了数值模拟,但是模拟的水舌是二维的,且研究的水舌尺度较小。
为了分析三维挑流水舌的运动特性,以及两股挑流水舌的碰撞特性,本文采用LBM方法对挑流水舌进行三维数值模拟研究。
2 格子玻尔兹曼方法

粒子运动的速度矢量见图1。

图1 D3Q19网格模型与粒子速度向量
3 挑流水舌空中运动数值模拟
3.1 计算模型与参数设置 采用长江水科院[20]对泄洪雾化概化模型,进行数值模拟研究,如图2所示,泄水建筑物长2.3 m,高1.7 m,宽0.28 m,出口挑坎挑角20°。数值模拟工况采用了典型的实验工况,即水头0.244 m,水头落差2.05 m。

图2 数值模拟几何模型
3.2 模型参数设置 模型采用xflow两相流计算模型,分别为液体相和空气相,液体相密度为998.3 kg/m3,动力黏度为0.001 Pa·s。空气相密度为1.225 kg/m3,动力黏度为1.7894 10-5Pa·s。
由于时间步长和解析度直接关系到计算结果的精度和计算效率。所以在保证计算结果精度的同时还必须考虑计算时间。经多方面考虑以及多次试算之后,选择时间步长为0.001 s,解析度为0.03 m最为合适。
环境参考压力取一个标准大气压,边界条件1、2截面采用压力进口条件,3截面采用压力出口,相对压力都设置为0。其余面均设置为自由滑移壁面边界条件。
3.3 水舌风场计算结果 图3为t=2.98 s时的水舌风场的空间分布计算图,从图中可以比较清楚的看出水舌与空气运动交界面,挑流水舌随着水舌的运动不断的掺气扩大。水舌的运动带动周围的空气沿水舌方向运动,并且在水舌入水处,水舌表面空气流速与水舌的流速相近风速达到6 m/s,风向沿水舌速度方向。

图3 水舌风场的空间分布
由于水舌下缘在临近下游水面区域与下游水面形成一个相对闭塞的空间,特别时水舌入水附近,如图3(c)所示,水舌下缘的风场情况相较于水舌上缘相对更加的复杂,在水舌下沿出现较多的漩涡流场,如图3(d)所示。从图中可以看出水舌入水与下游水面碰撞,引起下游水面液滴飞溅,在下游水面形成一个与水舌入水面为边界的水滴喷溅区,并且沿水舌外缘入水区域的喷溅水滴,由于水舌入水夹角的关系,沿x方向的速度分量比其他区域的大。这也是泄洪雾化的主要雾源。
3.4 水舌运动特性验证分析 数值模拟采用了典型工况:水头0.244 m,水头落差2.05 m。对水舌的内缘和外缘轨迹和挑距,以及水舌的厚度沿水舌轨迹的变化等进行分析。
采用2次多项式对水舌的內缘、外缘以及中心内线进行拟合,分别得到:
內缘曲线表达式为:

外缘曲线表达式为:

中心线曲线表达式:

挑流水舌的外缘和内缘,分别与文献[5]做了对比,如图4所示。

图4 挑流水舌外缘和内缘的空间变化
从图4中可以看出,两者的水舌轨迹基本一致。在水舌的中间段,本文的外缘线比文献[5]的结果偏高,中间段水舌的扩散速度比文献[5]更快。
图5为水舌流速与下游水位截面位置的体积分布计算结果,水舌入水的速度在6 m/s左右。水舌内缘挑距约为2.8 m,外缘挑距约为3.5 m,横向宽度约为0.75 m。与实测数据对比误差分别为9.6%、7.9%、7.1%,如表1所示,可以看出挑距的模拟值相对实测数据偏低。水舌入水的形状如图5(b)所示,大致为一个圆角的矩形趋近于椭圆形,与文献[21]中单孔泄洪实验的水舌落水形状基本一致,这可以为水舌入水喷溅雾源的进一步研究提供参考。

表1 水舌挑距实测值[17]与模拟值的对比

图5 挑流水舌俯视图与水舌入水截面图
图6为水舌模拟与理论计算的厚度与长度关系变化图,其中H为水舌厚度/m,H0为水舌初始断面厚度/m,S为水舌长度/m。通过挑流水舌厚度与水舌长度的关系图,可以将水舌的厚度变化可以分成三个阶段,如图的Ⅰ、Ⅱ、Ⅲ阶段。

图6 挑流水舌厚度与水舌长度的关系
Ⅰ阶段水舌扩散缓慢,且水舌的厚度的增长与水舌长度呈线性关系,这是由于Ⅰ阶段水舌尚有核心区存在,水舌掺气量少,水体比较密实。
Ⅱ阶段水舌的厚度扩散速度先加快后慢慢变缓,这是因为由于水舌速度的增加,空气对水舌的阻力增加,这样水舌内部的紊动也就随之增加,引起水舌的破碎和大量掺气,使水舌厚度快速的增加,随着水舌掺气的增加逐渐趋于饱和,使得掺气速度逐渐趋于变缓,水舌的厚度增加速度变缓。
Ⅲ阶段为水舌的均匀扩散段,水舌的厚度的增长与水舌长度呈现近似线性变化。这与文献[1]中通过实验数据分析,将水舌厚度的变化分为三个不同变化区段,即:(1)出口缓扩段;(2)水舌急剧扩散段;(3)水舌均匀扩散段;结论基本一致。
如图7为水舌速度与水舌长度的关系对比图,其中的文献[5]-v、文献[5]-vx、文献[5]-vy为采用文献[5]的数学模型,忽略空气阻力情况下的计算结果。从图中可以看出本文-v和文献[5]-v随着S增加先减小后增加、本文-v和文献[5]-v的上升阶段,本文-v相对与文献[5]-v的值偏小,这是因为采用文献[5]数学模型计算水舌时,没有考虑空气阻力以及水舌风场的影响。

图7 水舌速度与水舌长度的关系
本文-vx值随着水舌挑S的增加而减小,而文献[5]-vx水舌由于没有考虑空气阻力的影响,水舌速度文献[5]-vx的值随着水舌挑距S的增加几乎不变。
本文-vy和文献[5]-vy随S增加先减小到0后增加,当本文-vy和文献[5]-vy等于0时,水舌上升到最高点。本文-vy与文献[5]-vy随S变化趋势基本是一致,这是由于在y方向水舌虽然受重力和空气阻力以及水舌风场的共同作用,但是重力起主导作用。
3.5 水舌涡量分析 涡量为流体速度的旋度:
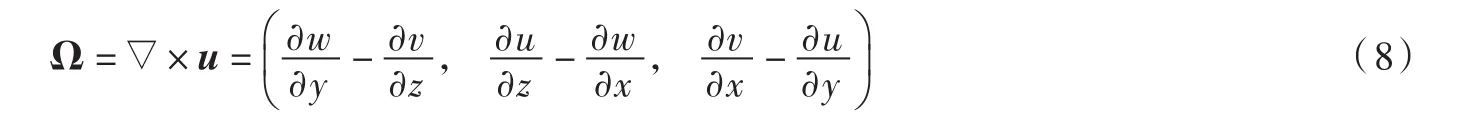
涡量是描写旋涡运动的重要物理量之一,在xy平面取水舌的中心平面得水舌的中间截面的涡量云图,即涡量在z轴的投影用Ωz表示,如图8所示。从图中可以看出水舌的上下表面在初始阶段Ωz远远高于内部水舌,这是因为水舌初始阶段掺气并不充分,仅仅外部水舌与空气作用,使得水舌的上下表面的Ωz远远高于内部水舌。这也是水舌掺气的重要影响因素,随着水舌的掺气量不断变大,Ωz向水舌的内部输运,在水舌的末端Ωz达到最大,Ωz达到139 s-1。

图8 水舌中心截面涡量云图
4 水舌碰撞的数值模拟
格子Boltzmann方法可以更加容易的实现两股水舌的碰撞,以及由于水舌碰撞而形成的相对复杂的水汽交界面,如图9所示。

图9 两股水舌碰撞水舌速度分布图
图9和图10分别为水舌碰撞的数值模拟图与文献[22]中水舌碰撞的实验图象。从图中可以看出两者的碰撞水舌形态基本一致,水舌经过碰撞后,水花四溅,水舌在碰撞后形成一个锥形的射流形态,并且由于两股水舌的碰撞形成的压力波影响,使得上股水舌的下表面破碎形成一股反向微射流,微射流以液滴为主且运动状态较为复杂,但其大多数液滴的运动方向与水舌的运动方向相反。这为进一步研究多股水舌泄流,以及水舌入水喷溅等复杂情况提供参考。

图10 两股水舌碰撞的试验结果图[22]
5 结论
本文采用格子Boltzmann方法针对三维挑流水舌以及两股水舌的碰撞进行数值模拟研究,得到如下结论:
(1)格子Boltzmann方法能很好的模拟泄洪挑流水舌和水舌风场,水舌的运动界面清晰可见。并且不用对水舌的周围的大片区域进行网格划分,计算更加便捷,效率更高。水舌内缘挑距约为2.8 m,外缘挑距约为3.5 m,横向宽度约为0.75 m。与实测数据对比误差分别为9.6%、7.9%、7.1%,挑距的模拟值相对实测数据偏低。为泄洪挑流水舌的流场研究提供新的方法。
(2)挑流水舌在初始阶段由于水舌与空气的相互作用,使得水舌的上下表面的Ωz远远高于内部水舌,这也是水舌掺气的重要影响因素,随着水舌的掺气量不断变大,Ωz向水舌的内部输运,在水舌的末端涡量达到最大,涡量达到139 s-1。
(3)格子Boltzmann方法可以对两股水舌的碰撞进行模拟,水舌碰撞的数值模拟与实验条件下水舌运动形态基本一致,水舌经过碰撞后,水花四溅,水舌在碰撞后形成一个锥形的射流形态,并且由于两股水舌的碰撞形成的压力波影响,使得上股水舌的下表面破碎形成一股反向微射流。为多孔泄流的复杂情况,水舌的运动特性以及流场研究提供参考。

