水平荷载-扭矩耦合作用下斜桩承载变形特性数值模拟

曹卫平,李 贺,陶 鹏

(1.西安建筑科技大学土木工程学院,陕西 西安 710055; 2.陕西省岩土与地下空间工程重点实验室,陕西 西安 710055)

输电塔、码头和海洋工程中常用斜桩抵抗风、海浪、土壤压力等较大的横向荷载[1]。与直桩相比,斜桩具有更高的侧向水平承载力[2],但由于斜桩桩身的轴线与建筑物所在平面并不垂直,导致斜桩在受到外部荷载作用时的承载变形特性与直桩有较大的不同。因此,对斜桩开展在水平荷载H和扭矩T耦合作用(H-T耦合作用)下的荷载变形特性和承载性能的研究对斜桩基础的设计具有重要意义。

桩基承载变形问题是国内外有关学者广泛关注的问题[3-5]。例如:Zhang等[6]通过离心模型试验研究了循环荷载作用下桩的变形特性,发现随着循环次数的增加,桩周土体的刚度逐渐减小;Ramadan等[7]通过对不同桩身倾角下受荷斜桩的桩身弯矩及位移分析,认为上拔荷载与水平荷载对桩身内力有着较明显的影响;Meyerhof等[8]通过模型试验研究了倾斜荷载作用下斜桩的变形性状,给出了桩顶水平位移的影响曲线;吕凡任[9]通过模型试验和现场试验开展了对倾斜荷载作用下斜桩基础的承载性状研究;曹卫平等[10-11]基于砂土中的斜桩模型试验和数值模拟软件,分别研究了竖向荷载和水平荷载作用下斜桩承载性状,分析了桩身倾角和长径比对斜桩承载力的影响;赵爽等[12]基于数值模拟软件,研究了砂土中各方向水平荷载与倾斜面斜交作用下斜桩单桩的变形及承载特性。也有部分学者研究了H-T耦合作用下桩的承载特性。例如:邹新军等[13]进行了H-T耦合作用下直桩的模型试验,并探讨了施加荷载的顺序对单桩的影响,得出无论是先施加水平荷载还是扭矩,都会使得单桩的扭矩或水平承载力降低,但先施加水平荷载对桩的承载力影响比先施加扭矩影响更大;郭沛翰等[14]在邹新军等[13]两种荷载作用的基础上添加了竖向荷载作用,完成了直桩室内砂土地基的模型试验,得到了3种荷载共同作用下对单桩的影响曲线和承载力计算公式。

目前对斜桩的承载变形研究大多只分析单个荷载作用下的变形情况,对涉及两个及多个荷载耦合作用下斜桩变形的研究较少,而H-T耦合作用对桩的影响研究大多只是针对直桩,对斜桩开展的相关研究较少。本文采用ABAQUS数值软件对斜桩在H-T耦合作用下的承载特性进行数值模拟,分析H-T耦合作用下桩身倾角对斜桩承载特性的影响,研究斜桩桩-土接触压力及摩阻力沿桩身的分布特征。

1 有限元模型

1.1 数值模型

本文所建立的数值模型如图1所示,为消除土体边界效应,桩周土计算范围取30D(D为桩径),桩端底部土层厚度取10D[15-16]。桩顶承受H-T耦合作用,水平荷载和扭矩为等比例同时施加,其中水平荷载垂直作用于斜桩桩身倾斜面,即水平荷载作用于斜桩所在平面以外,扭矩方向为z轴正向。

图1 有限元模型与计算网格

采用ABAQUS数值软件对H-T耦合作用下的斜桩承载性状进行模拟分析,选取线弹性模型模拟桩体,Drucker-Prager模型模拟土体变化。桩-土界面相互作用通过ABAQUS数值软件中桩-土界面接触算法实现,选择桩侧与桩端表面为主控面,土侧与桩端土表面为从属面。桩-土接触界面法向作用采用硬接触的方法模拟,切向作用采用罚函数模拟,桩-土接触界面间的摩擦系数μ采用μ=tan(0.75φ)计算,其中φ为桩周土的内摩擦角[15]。桩身网格密度均匀布置,土体网格密度根据与桩身的距离由近至远沿径向由密到疏布置。桩身及土体单元均采用三维实体单元C3D8R[17]。

1.2 数值模型验证

为验证数值模型材料本构关系选取和计算参数设置的合理性,分别选取吕凡任等[18]和王书行[19]进行的现场载荷试验和模型试验进行验证分析。

吕凡任等[18]进行了软土地基上斜桩的现场试验研究,试验用斜桩桩长为15m,桩径为0.25m,桩身倾角为10°。在进行数值模拟时,参考文献[13-14],取钢桩密度为7.9t/m3;各土层的泊松比均取为0.3,土体剪胀角取6.5°。现场试验与数值模拟的对比结果如图2所示。

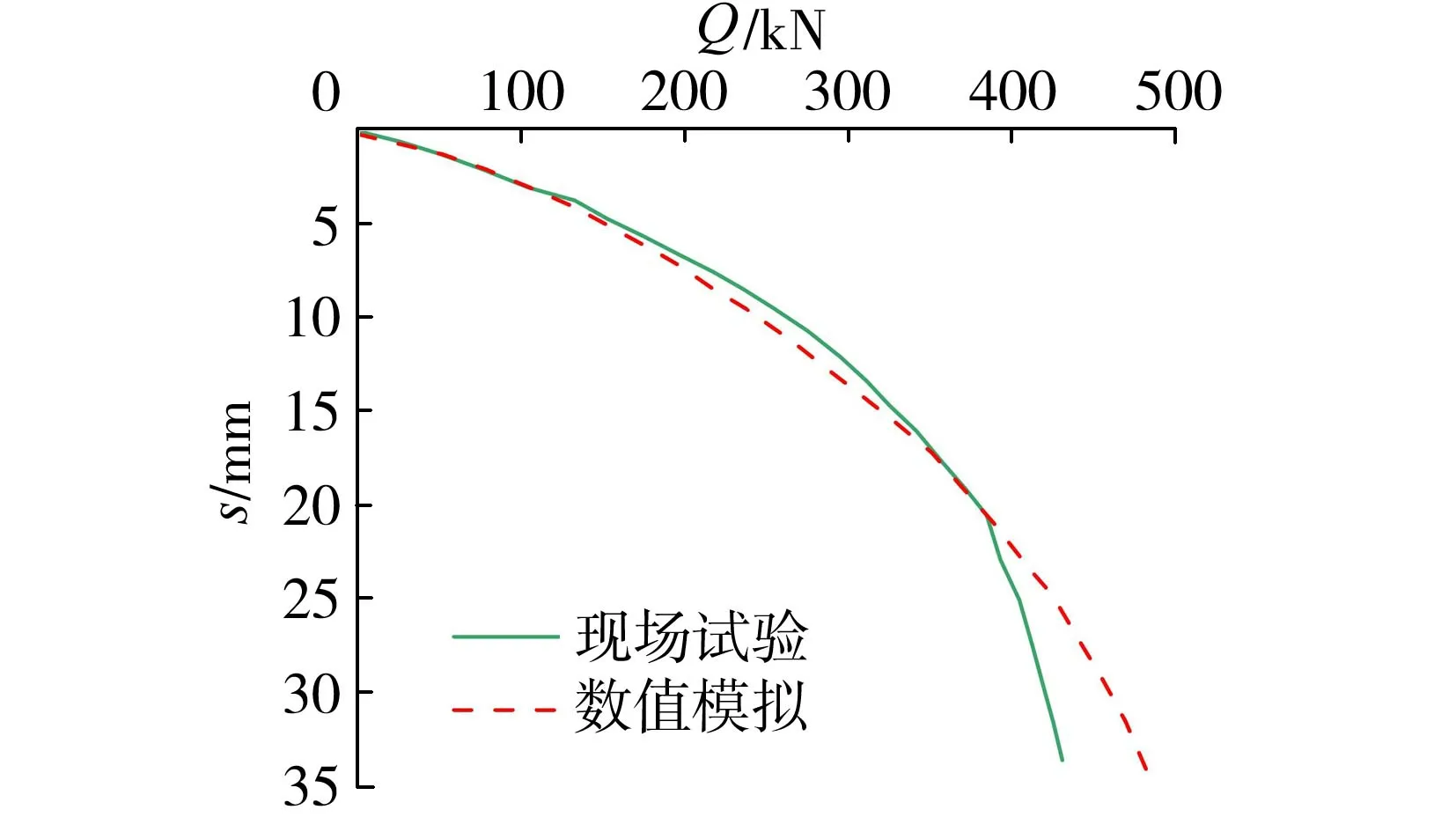
图2 现场试验与数值模拟结果对比

王书行[19]开展了饱和粉土地基中扭矩作用下直桩室内模型试验。试验用直桩材料为钢管,桩长为6m(入土深度为3.41m),桩径为114mm,壁厚为4.5mm;土层密度为1.7t/m3,有效内摩擦角为30°,有效黏聚力为1kPa,取粉土地基的压缩模量为9.9MPa,泊松比为0.3,模型土体弹性模量取压缩模量的4倍。模型试验与数值模拟的对比结果如图3所示。

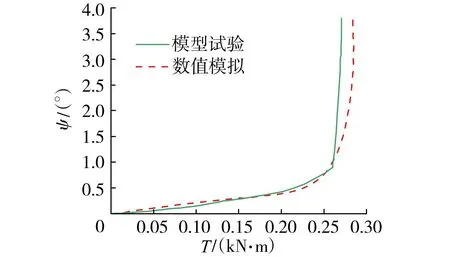
图3 模型试验与数值模拟结果对比

图2和图3分别为荷载(Q)-沉降(s)曲线和桩顶扭矩(T)-扭转角(ψ)曲线,结果表明,数值模拟结果与现场试验和模型试验的结果吻合较好,说明本文建立的数值模型是合理的,能较好地反应桩基与地基土之间的相互作用。

1.3 数值模拟方案

本文基于吕凡任等[18]的研究背景,对H-T耦合作用下斜桩的承载变形特性进行有限元数值模拟分析,模拟桩桩径为0.5m,桩长为15m,密度为2.4t/m3,泊松比为0.2,弹性模量为31.5GPa。土层参数如图4所示,各层土的泊松比均取为0.3,土体剪胀角可取为6.5°[11]。

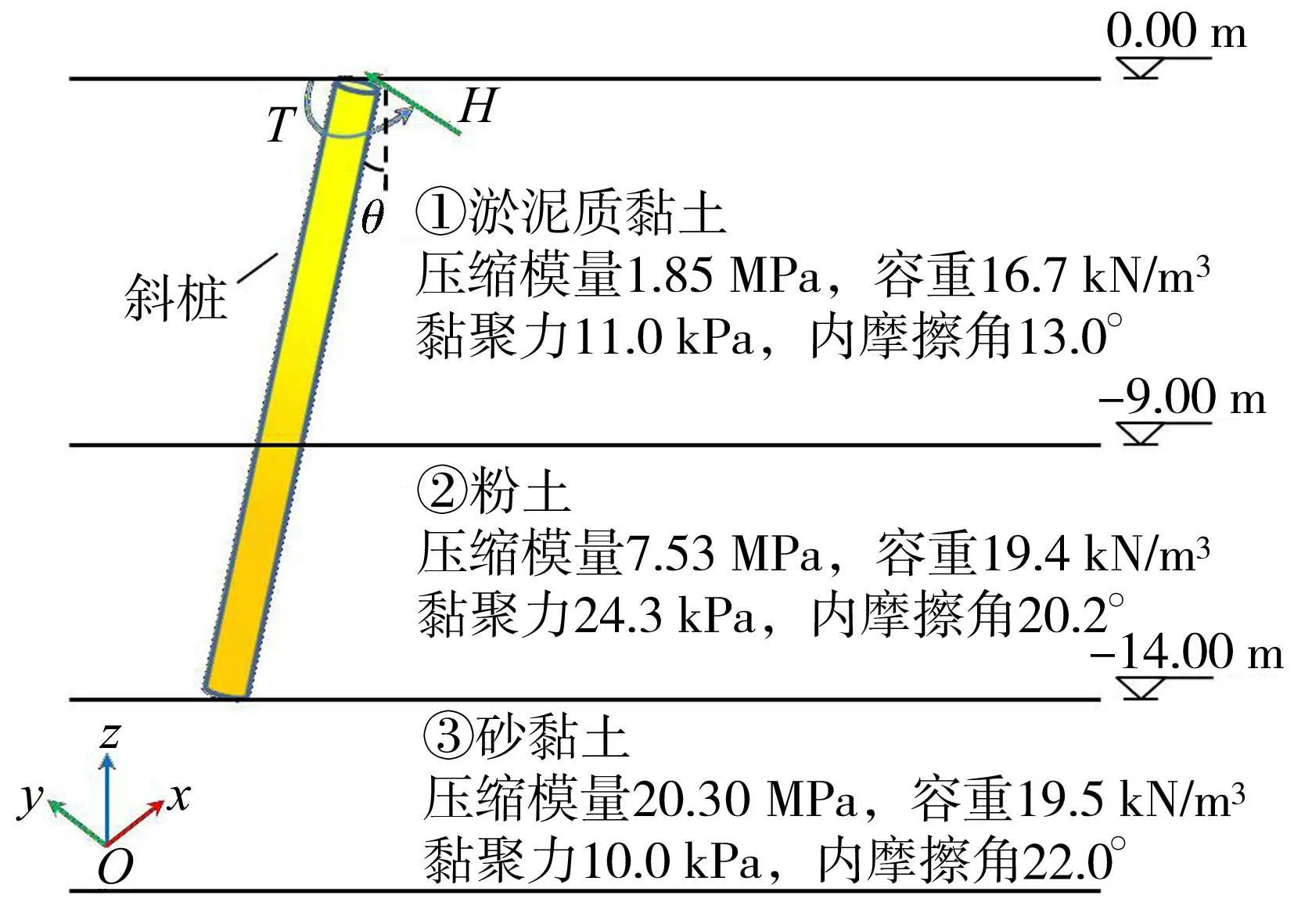
图4 数值模拟土体示意图

斜桩数值模拟共分为4组,分别模拟桩身倾角、桩-土刚度比、荷载偏心距、桩身长径比等4种影响因素对斜桩承载变形特性的响应,模拟方案如表1所示,除第一组包含4根桩外,其他3组均只含3根桩。

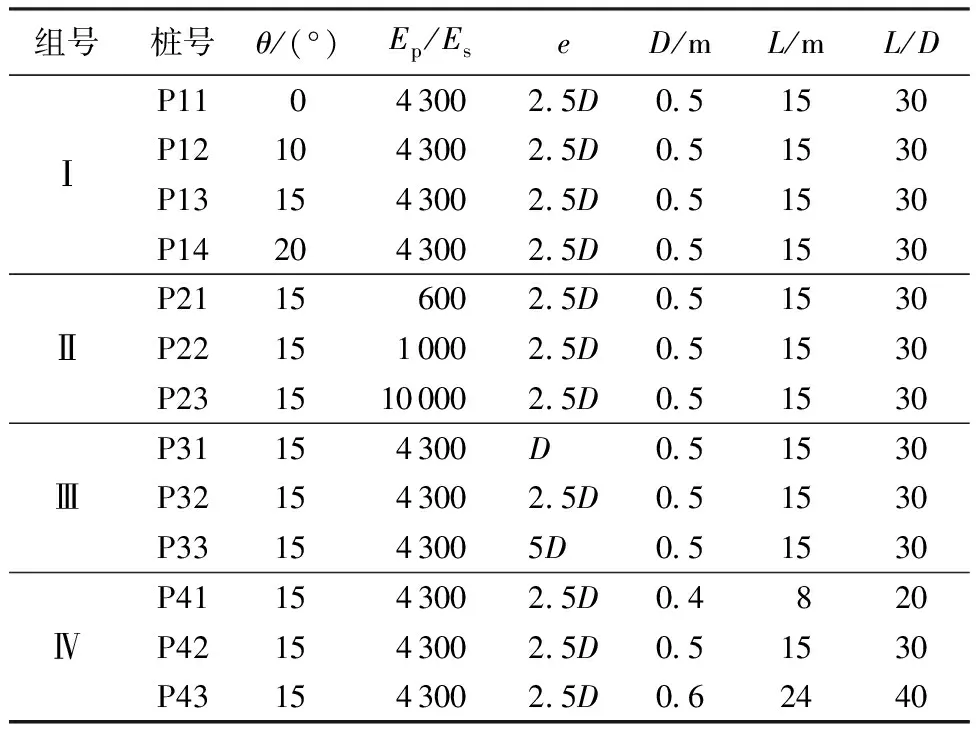
表1 数值模拟方案

2 直桩与不同桩身倾角斜桩的承载变形特性

2.1 桩顶扭转角和位移

图5为直桩和不同桩身倾角斜桩桩顶扭矩-扭转角曲线,当曲线出现急剧上升变化时即可认为桩顶扭矩达到极限扭矩而导致桩身破坏。由图5可见,桩身倾角越大,斜桩桩顶极限扭矩和极限扭转角越大。定义α、β分别为斜桩对直桩极限扭矩和极限扭转角的提高幅度,表2为不同桩身倾角下斜桩的极限扭矩和极限扭转角相对直桩的提高幅度。图5和表2的结果表明,与直桩相比,斜桩能提高桩身受扭承载力,且桩身倾角越大,提高幅度越大。

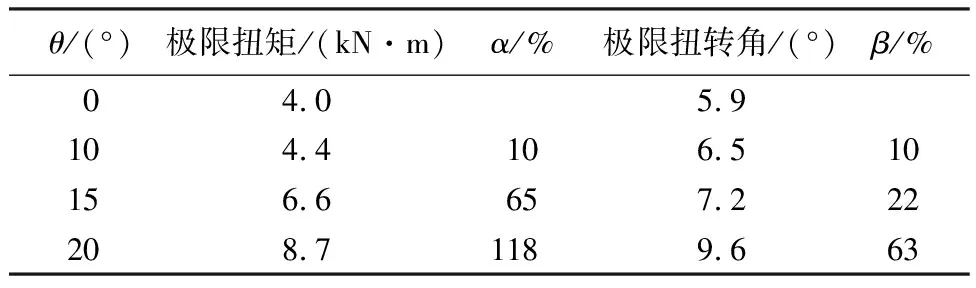
表2 桩身倾角对斜桩桩顶扭转承载变形特性的影响

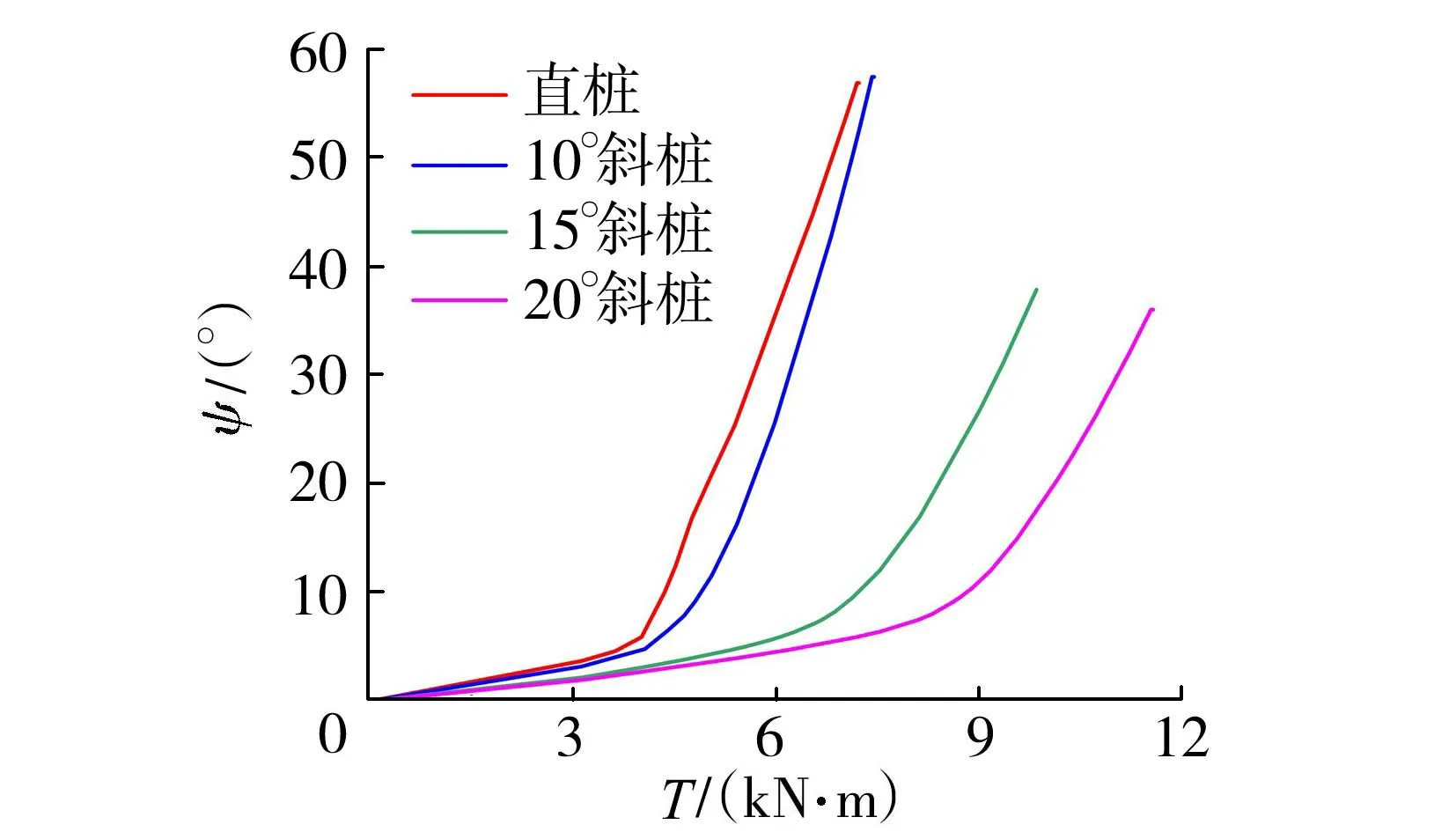
图5 桩顶扭矩-扭转角曲线

从表2和图5中还可以看出,通过增大桩身倾角可以增加桩身极限扭矩,但同时要注意桩身倾角越大的斜桩其桩顶扭转角相比其他斜桩也越大,如20°斜桩的极限扭转角相对直桩的提高幅度为63%。在实际工程中可以通过增大一定的桩身倾角来增加桩的受扭承载力,但是要考虑扭转角的极限值,同时更要考虑更大变形的不利影响。

直桩和不同桩身倾角斜桩桩顶水平荷载(H)-位移(s)曲线如图6所示。结合图5并分析曲线拐点可知,在桩身达到最大扭矩前,桩顶水平位移与桩顶水平荷载呈线性正相关关系;在桩顶水平荷载相同的情况下,桩顶水平位移与桩身倾角呈正相关关系。

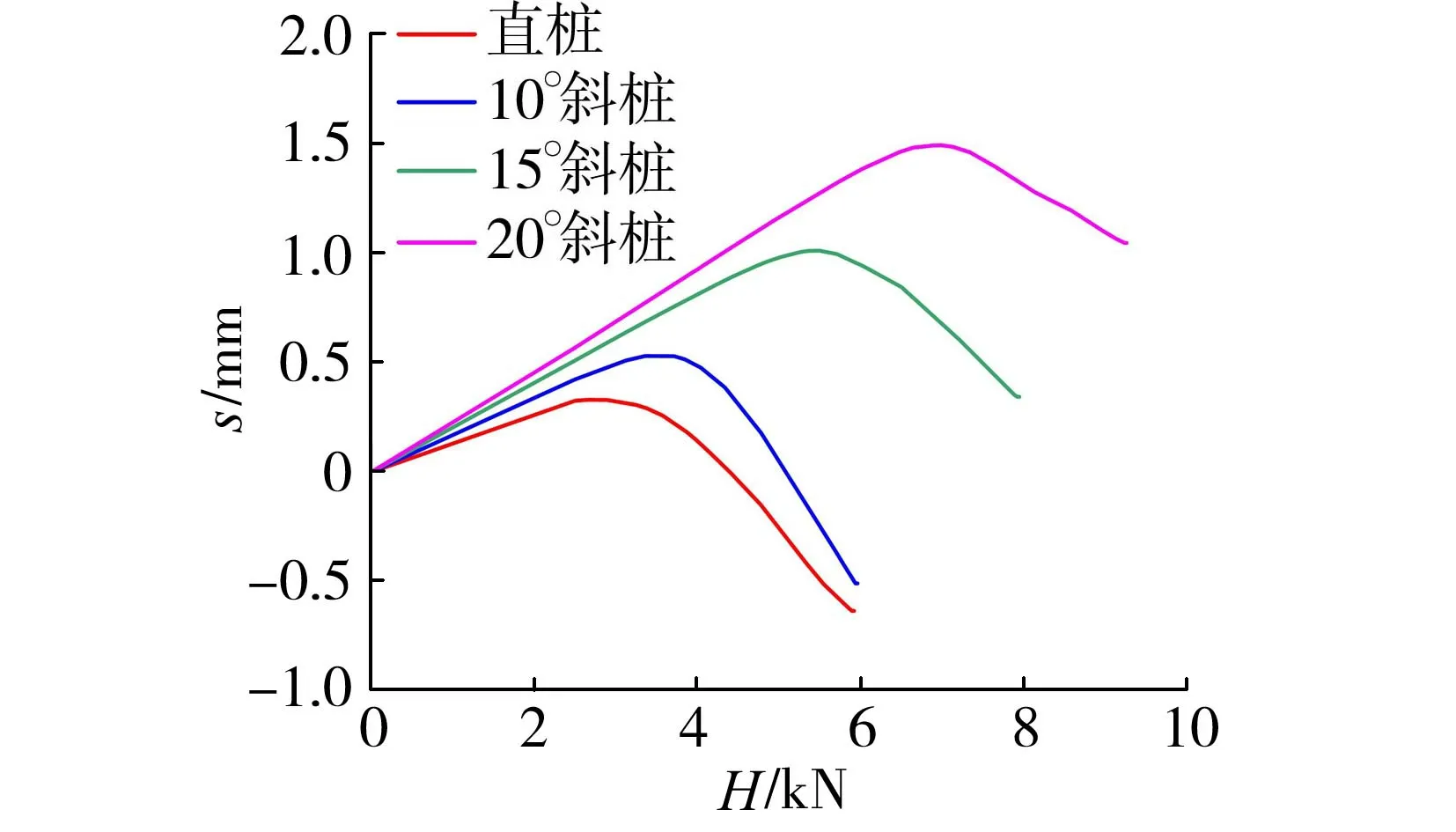
图6 桩顶水平荷载-位移曲线

斜桩桩顶在受到H-T耦合作用时,参考赵春风等[20]研究成果和JGJ106—2014《建筑基桩检测技术规范》,取泥面处单桩水平位移达到0.1D时的水平荷载为单桩水平极限承载力。由表2、图6以及邹新军等[21]的试验结果可知,斜桩达到极限扭矩时,相应水平荷载作用下的桩顶水平位移均远小于0.1D,即此时尚未达到斜桩的水平极限承载力,因此在H-T耦合作用下,斜桩桩身为受扭破坏,即相对水平极限承载力而言桩身的受扭承载力较低。

2.2 桩身位移和内力

选取H=3.2kN、T=4kN·m,得到H-T耦合作用下不同桩身倾角时桩身侧向水平位移沿桩身相对深度(桩身沿z轴入土深度与总桩长L的比值)的分布曲线如图7所示(位移以沿y轴正向为正)。从图7可以看出,随着桩身相对深度的增大,直桩和不同桩身倾角斜桩桩身侧向水平位移发展区均分布在桩顶部以下桩身相对深度0.3以内。另外,最大侧向位移均出现在桩顶,随后随着深度逐渐减小。直桩和不同桩身倾角斜桩的反弯区基本都处于3D～9D之间,斜桩反弯区沿桩身相对深度范围分布与直桩相近,范围基本一致,且反弯区最大位移与桩顶水平位移相比很小,可忽略不计。这表明在H-T耦合作用下,桩身侧向水平位移主要在桩周上部区域有变化。

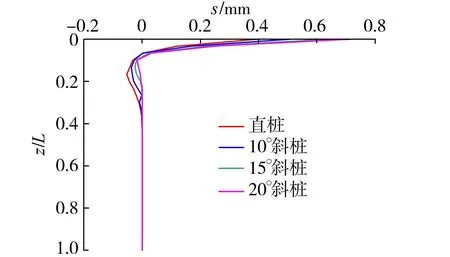
图7 桩身侧向水平位移沿桩身相对深度的分布曲线

图8为H=3.2kN、T=4kN·m时,在H-T耦合作用下直桩和不同桩身倾角斜桩桩身扭矩沿桩身相对深度的分布曲线。由图8可知,直桩和不同桩身倾角斜桩的扭矩沿桩身分布,且随着桩身相对深度的增大,桩身扭矩从桩顶的最大值一直逐渐减小,到桩端减到最小,接近于0。这是由于桩侧摩阻力发挥抵抗作用使得桩身扭矩逐渐减小,在相同的深度下,桩身倾角越大,桩所受的扭矩越小。因此工程上可以通过提高一定的桩身倾角来增强桩身受扭能力。

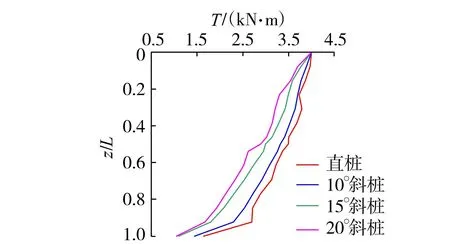
图8 桩身扭矩沿桩身相对深度的分布曲线

图9为H=3.2kN、T=4kN·m时,在H-T耦合作用下直桩和不同桩身倾角斜桩桩身弯矩(M)沿桩身相对深度的分布曲线。由图9可知,斜桩的桩身弯矩均大于直桩,且桩身倾角越大,桩身弯矩越大。直桩和不同桩身倾角斜桩的桩身弯矩都是随着桩身相对深度的增大先迅速增大到最大值,20°斜桩桩身弯矩最大,最大值出现在1.8D左右处,随后桩身弯矩沿桩身相对深度急剧减小为0。与图8结果对比可知,在桩身相对深度0.15范围内,桩身弯矩对桩的影响较大,而扭矩则沿全桩均有分布。

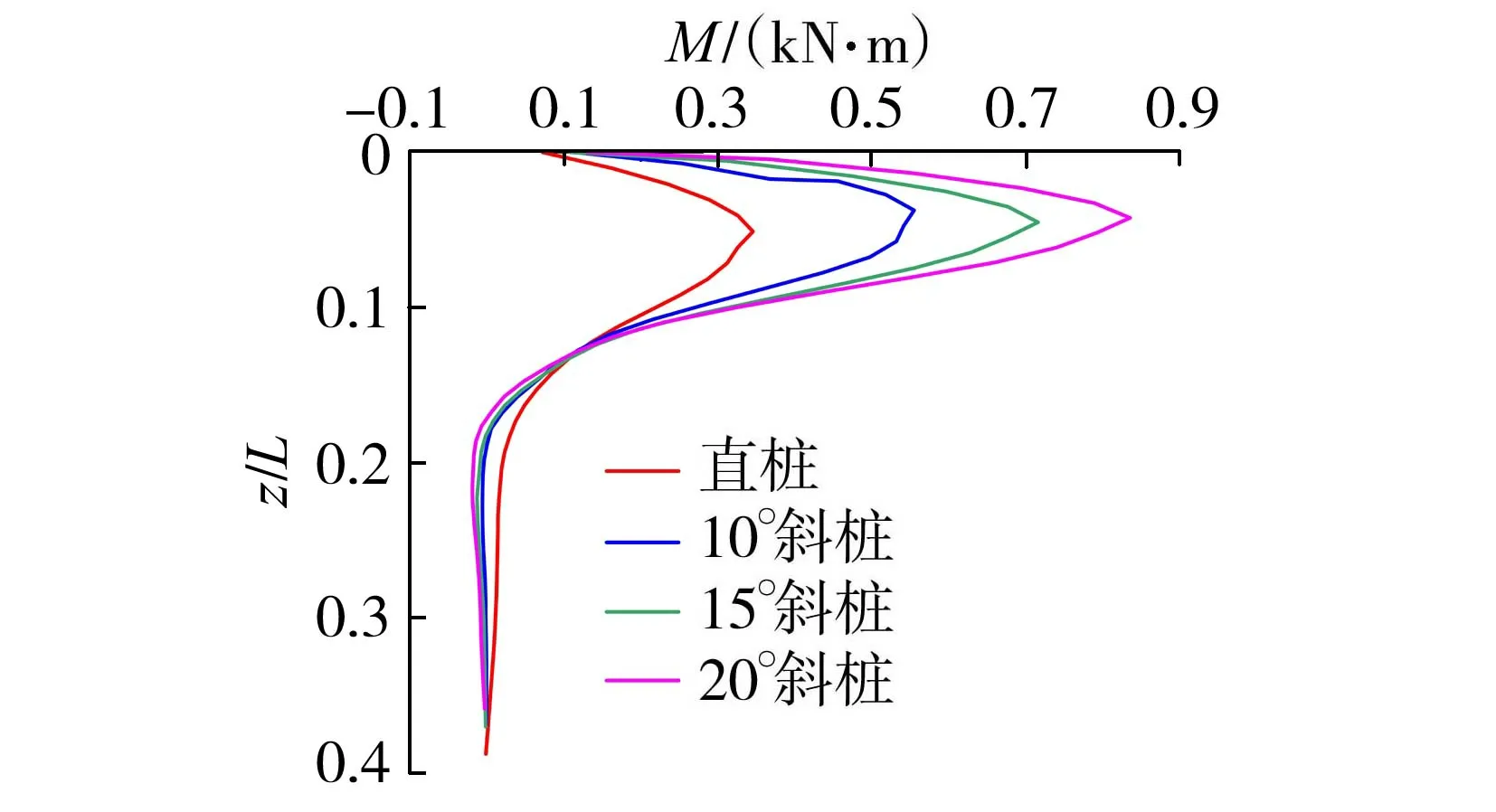
图9 桩身弯矩沿桩身相对深度的分布曲线

2.3 桩-土接触压力

由于桩顶水平荷载作用在斜桩桩身倾斜平面外,同时桩顶受到扭矩的影响,故导致桩-土接触压力不是轴对称的,因此选择沿斜桩桩身深度方向上的A、B、C、D 4条路径(图10)对桩-土接触压力进行有限元模拟。

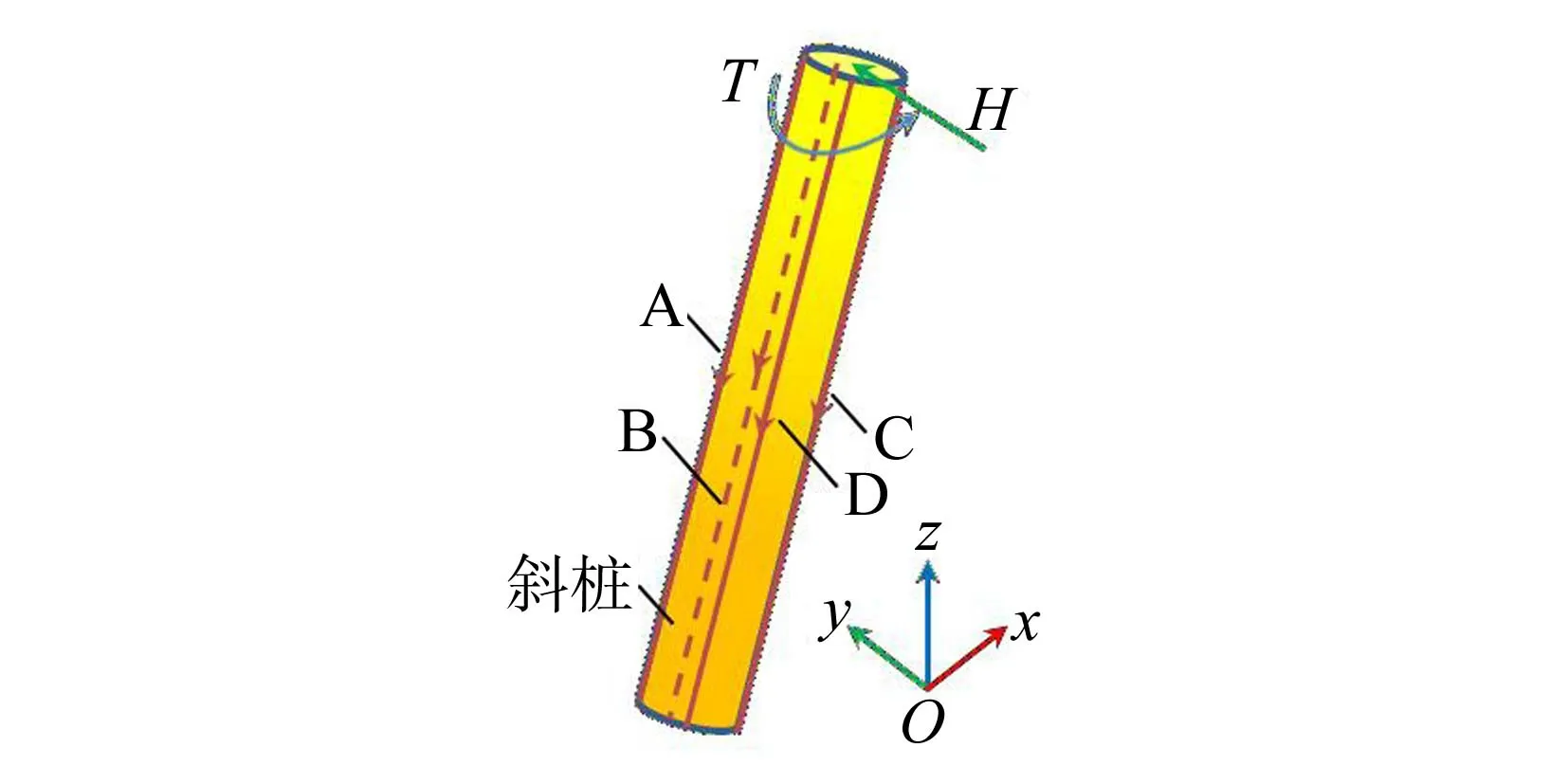
图10 桩-土接触压力路径

图11为15°斜桩在桩顶扭矩为4kN·m时桩-土接触压力(p)沿桩身相对深度的分布曲线,从图11可知,不同路径侧的桩-土接触压力有着较为明显的不同:在桩顶向下桩身相对深度0.3范围内,由于H-T耦合作用,沿B、C路径侧土体有脱离桩体的趋势,故B、C路径侧桩-土接触压力小于静止土压力,而沿A、D路径侧土体有受到挤密的趋势,故A、D路径侧的静止土压力小于桩-土接触压力。这表明在H-T耦合作用下,B、C路径侧土体为卸荷,A、D路径侧土体受挤压。从卸荷侧来说,路径C侧桩-土接触压力小于B侧,这说明相比较路径B侧来说C侧土体脱离桩体的趋势更大。从挤压侧来说,路径A侧的桩-土接触压力大于D侧,这说明相比路径D侧来说A侧土体受到的挤压效应更大。

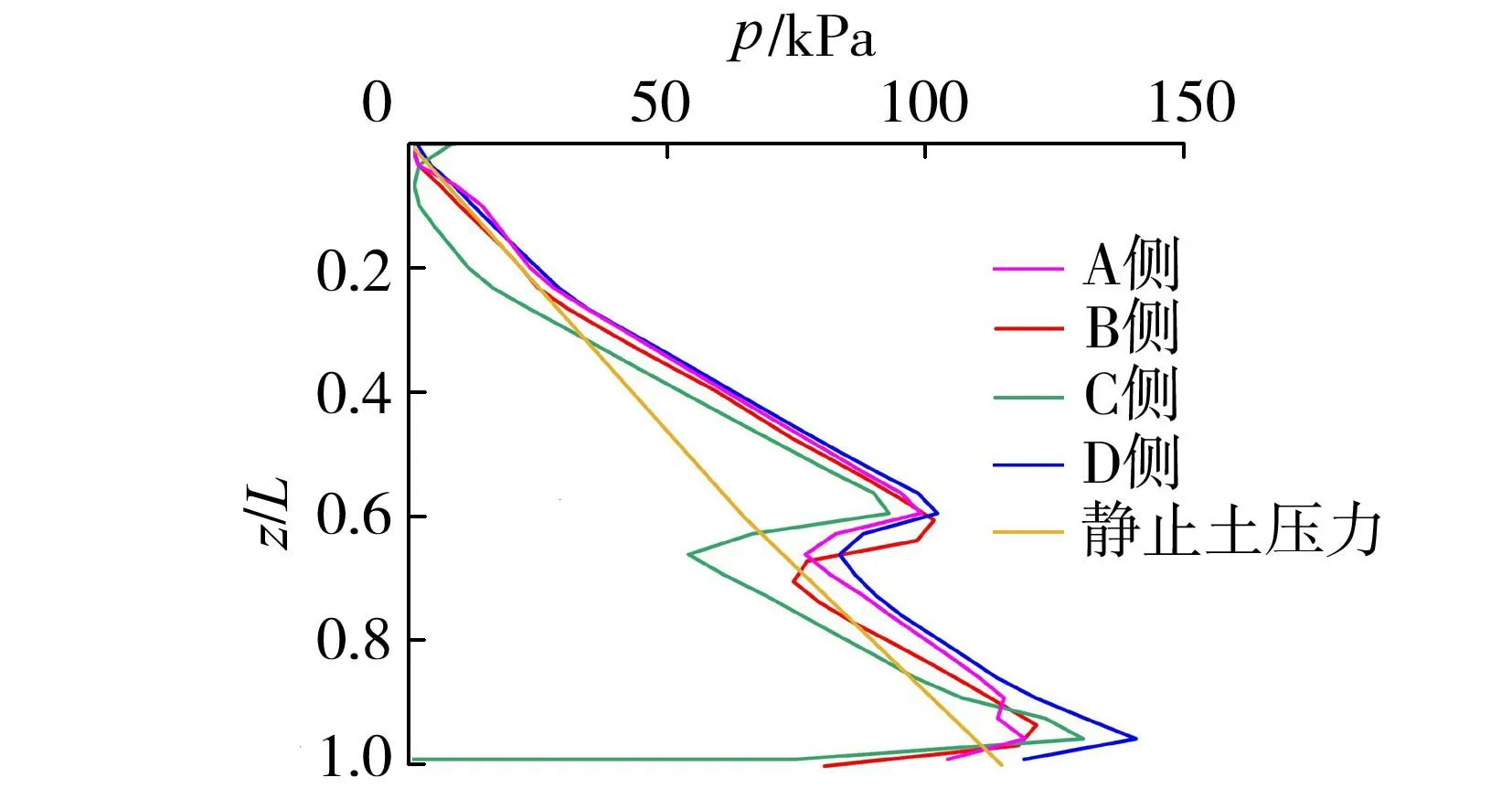
图11 15°斜桩桩-土接触压力沿桩身相对深度的分布曲线

2.4 桩侧环向摩阻力

图12为桩顶在H-T耦合作用下,直桩和不同桩身倾角斜桩的桩侧环向摩阻力(qsi)沿桩身相对深度的分布曲线,可以看出,斜桩桩侧环向摩阻力分布与直桩明显不同:直桩桩侧环向摩阻力一开始为0,而斜桩在桩顶以下一开始就有较大的摩阻力;直桩桩侧环向摩阻力沿桩身相对深度逐渐增大,而斜桩桩侧环向摩阻力沿桩身相对深度增大先减小,在桩身相对深度0.3处又反向沿桩身相对深度逐渐增大。同一深度位置处,桩侧环向摩阻力与桩身倾角成正比,即20°斜桩的桩侧环向摩阻力最大。这表明桩侧环向摩阻力的发挥程度与桩身倾角有关,倾角越大,发挥程度越大,且桩身上部区段的发挥程度要大于桩身下部区段。此外,对于桩身中下部区段(z/L=0.3～0.9),桩侧环向摩阻力沿桩身相对深度增大的一个原因是桩-土接触压力增大。

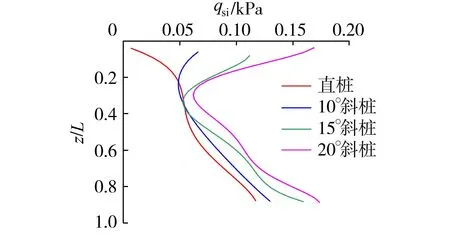
图12 桩侧环向摩阻力沿桩身相对深度的分布曲线

2.5 不同因素对斜桩桩顶扭矩-扭转角曲线的影响

图13～15分别为不同桩-土刚度比、荷载偏心距和桩身长径比影响下15°斜桩的桩顶扭矩-扭转角曲线,图中曲线均为陡升型,若以曲线急剧变化点对应的扭矩值作为斜桩的极限扭矩,可得到对应于不同影响因素的斜桩的最大扭转角。由此可知,在一定桩顶扭转角下,桩-土刚度比和荷载偏心距越大,斜桩所承受的扭矩越小,表明斜桩受扭承载力与桩-土刚度比和荷载偏心距呈负相关关系,但其影响程度较小。而在同一桩顶扭转角下,斜桩极限扭矩与桩身长径比呈正相关关系且影响较大,短桩的极限扭矩增幅较小,长桩的极限扭矩增幅较大。对于短桩,桩-土界面发生破坏,桩侧环向摩阻力为其提供了受扭承载力,故短桩的极限扭矩增幅较小。对于长桩,土体内部发生破坏,其受扭承载力主要由桩侧土体的内部剪切作用和桩-土界面的扭转剪切作用共同提供。综上,桩-土刚度比和荷载偏心距对斜桩极限扭矩的影响不大,而桩身长径比则对其影响较为显著。

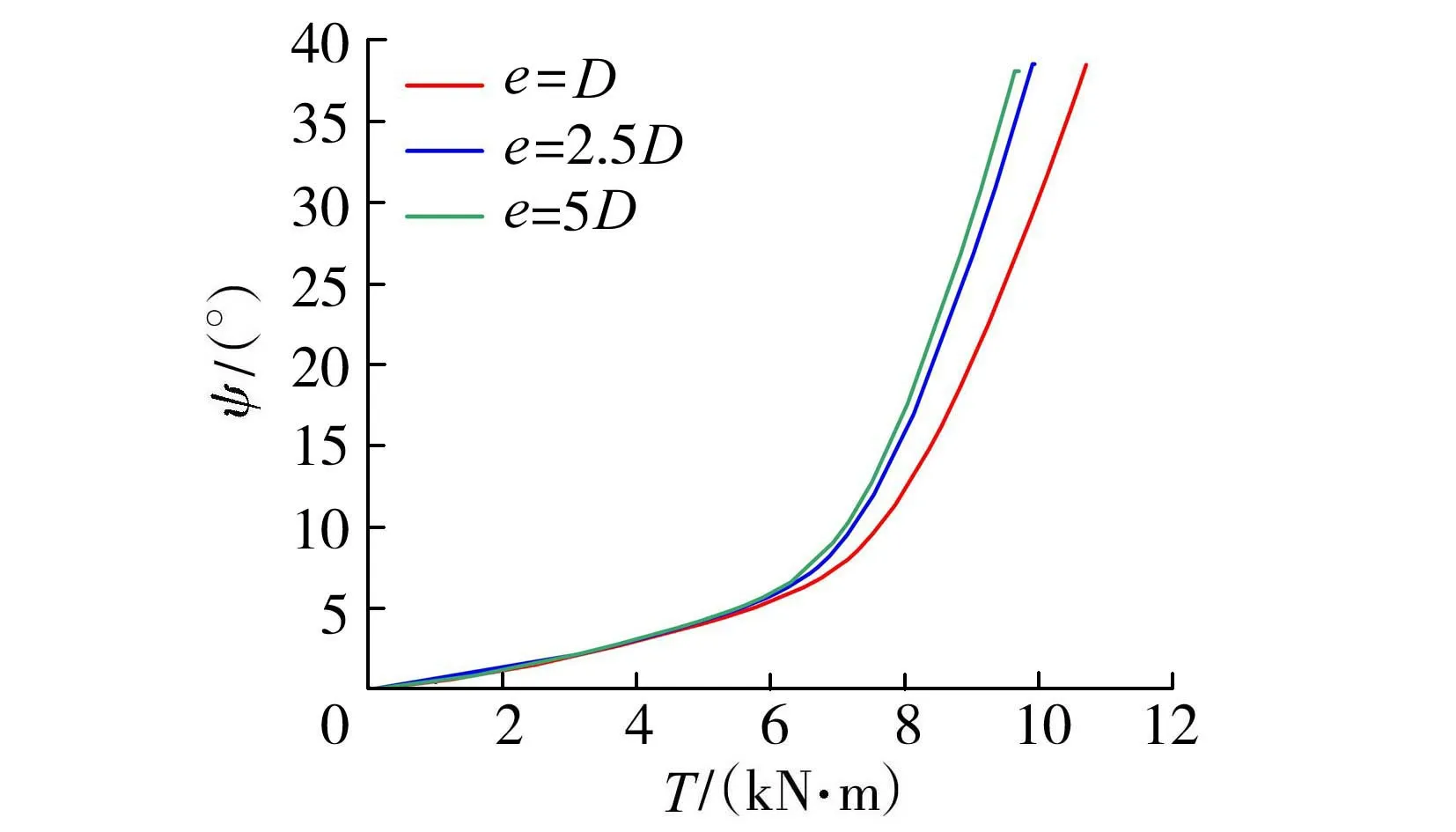
图14 不同荷载偏心距时的桩顶扭矩-扭转角曲线

如图15所示,对同一倾角(15°)的斜桩来说,若以同一桩顶扭转角作为极限值,则明显可以看出桩身长径比对受扭承载力的影响,即桩身长径比越大的斜桩其极限扭矩也越大,桩顶扭转角给定的前提下,扭矩与桩身长径比呈正相关关系。从图15还可以看出,虽然桩身长径比较大的桩其极限扭矩也较大,但其相应的桩顶扭转角也较大,即极限扭矩提高的同时也使得极限扭转角增大,因此在实际工程中可以通过增大桩身长径比来提高桩身受扭能力,但是要注意桩顶扭转角的极限值不能过大。

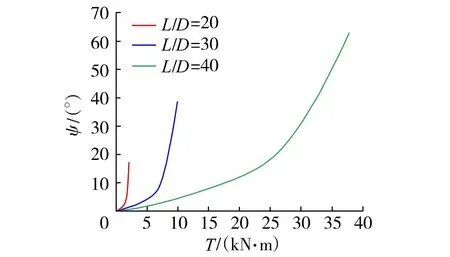
图15 不同桩身长径比时的桩顶扭矩-扭转角曲线

3 结 论

a.H-T耦合作用下,斜桩桩身表现为受扭破坏,斜桩相比直桩有更高的受扭承载力,且桩身倾角越大,承载力越高。

b.在桩顶H-T耦合作用下,斜桩桩身扭矩沿桩身分布,不存在临界桩长的问题。斜桩桩身扭矩小于直桩,最大值出现在桩顶,沿桩身向下逐渐减小,在桩顶下同一截面位置处,斜桩桩身扭矩与桩身倾角呈负相关关系。

c.在桩顶H-T耦合作用下,相比直桩,斜桩更有利于桩侧环向摩阻力的发挥,桩身倾角越大,桩侧环向摩阻力的发挥程度越大,且桩身上部区段的发挥程度要大于桩身下部区段。

d.斜桩极限扭矩与桩-土刚度比和荷载偏心距呈负相关关系,但两者对极限扭矩影响程度较小;而桩身长径比与斜桩极限扭矩呈正相关关系且影响程度较大。