基于核心素养的三道导数试题的命题手法探析*
福建省福清第三中学 (350315) 何 灯
福州教育研究院 (350001) 余小萍
极值点偏移问题以导数为背景考察学生综合运用各类知识和思想方法解决函数问题的能力,是值得深入探究的课题,更是培养学生数学核心素养的好素材.近期,笔者在整理各地市模拟试卷时发现一类极值点偏移问题连续在三个地市出现(本文中的题1-3),且其中涉及到三角函数,此种不寻常现象引起笔者的关注,遂进行了一些思考,此处整理成文,与同仁交流.
1、识得庐山真面目——再现模拟试题
题1 (2023届漳州一中高三第一次阶段考试22)已知函数f(x)=2x-alnx+4a(a∈R).(1)讨论函数f(x)的单调性;(2)令g(x)=f(x)-sinx,若存在x1,x2∈(0,+∞),且x1≠x2时,g(x1)=g(x2),证明:x1x2 评注1:由g(x1)=g(x2)可得a(lnx2-lnx1)=2(x2-x1)-(sinx2-sinx1). 评注2:由f(x1)=f(x2)得a(lnx2-lnx1)=2(x2-x1)-(sinx2-sinx1),与题1恒等式相同. 评注3:由f(x1)=f(x2)得-m(lnx2-lnx1)=2(x2-x1)-(sinx2-sinx1),令-m=a,可得与题1相同的恒等式. 上述三个试题问题(2)设问相同,下面仅针对题3问题(2),给出具体的解析. 解析:不妨设0 m(lnx2-lnx1)=(2x1-2x2)+sinx2-sinx1. 通过上述对试题求解的逆向推演,不难管窥命题者的命题手法.笔者将其整理为如下六个步骤. 步骤一(选取函数模型u(x)):选择函数u(x),使得x∈(0,+∞),有u(x)≥0.题1-3选取的函数模型u(x)=1-cosx. 步骤二(求积获得函数h(x)):令h′(x)=u(x),通过对u(x)求积分,得到函数h(x)(以此保证h(x)在(0,+∞)上呈现出单调递增).题1-3积分求得函数h(x)=x-sinx. 步骤三(对h(x)赋值获得不等式):h(x)在(0,+∞)上呈现单调递增,设x2>x1,则h(x2)-h(x1)>0.题1-3得到x2-sinx2-x1+sinx1>0. 步骤五(构造题设函数f(x)):将步骤三与步骤四构建的不等式h(x2)-h(x1)>0与|λ|(lnx2-lnx1)>x2-x1相减,得到F(x1)≈F(x2),其中F(x)=x+h(x)-|λ|lnx.对F(x)增删某些项,得到题设函数f(x)(使得f(x1)=f(x2),题1中题设函数为g(x)).题1得到题设函数g(x)=2x-alnx+4a-sinx(在F(x)=2x-sinx-alnx的基础上,增补了4a);题2得到题设函数f(x)=2x-sinx-alnx(F(x)=2x-sin-alnx,取f(x)=F(x));题3得到题设函数f(x)=2x-sinx+mlnx(F(x)=2x-sin+mlnx,取f(x)=F(x)). 步骤六(进行合理设问):为了体现题目的梯度,让不同程度的学生都能充分发挥自己的水平,试题的第一问应当尽量简单(可以讨论相关函数的单调性、极值、最值、切线等,或铺设问题为第二问的研究埋下伏笔).第二问研究题设函数f(x),得到问题:若∃x1,x2∈(0,+∞),x1≠x2,使得f(x1)=f(x2),求证:x1x2<λ2.题1中问题(1)研究函数f(x)的单调性;题2中问题(1)研究题设函数f(x)相关不等式的恒成立求参数m的取值范围;题3中问题(1)研究函数g(x)的单调区间和极值.题1-3问题(2)均是验证x1x2<λ2(|λ|=a,-m)恒成立. 本环节,笔者尝试遵循上述六个步骤,命制两道相关试题,以期使读者对该类试题的命题流程能够更深入的理解. 命制题1步骤一(选取函数模型u(x)):选择函数u(x)=1-sinx,显然当x∈(0,+∞),有u(x)≥0. 步骤二(求积获得函数h(x)):对u(x)求积分,得到函数h(x)=x+cosx. 步骤三(对h(x)赋值获得不等式):设x2>x1,则x2-x1+cosx2-cosx1>0. 步骤四(借助对数平均不等式放缩):设定问题(2)待证不等式形式为x1x2<λ2,得到|λ|(lnx2-lnx1)>x2-x1. 步骤五(构造题设函数f(x)):将x2-x1+cosx2-cosx1>0与|λ|(lnx2-lnx1)>x2-x1相减,得到F(x1)≈F(x2),其中F(x)=2x+cosx-|λ|lnx,由此可设定题设函数f(x)=2x+cosx-alnx. 步骤六(进行合理设问):问题(1)的设定类似于题3,研究函数g(x)=f(x)-cosx的单调区间和极值.问题(2)设定为:若∃x1,x2∈(0,+∞),x1≠x2,使得f(x1)=f(x2),求证:x1x2 综合上述命制过程,得到如下新题: 题4 已知函数f(x)=2x+cosx-alnx. (1)求函数g(x)=f(x)-cosx的单调区间和极值; (2)若∃x1,x2∈(0,+∞),x1≠x2,使得f(x1)=f(x2),求证:x1x2 命制题2步骤一(选取函数模型u(x)):选择函数u(x)=ex-1,可证当x∈(0,+∞),有u(x)≥0. 步骤二(求积获得函数h(x)):对u(x)求积分,得到函数h(x)=ex-x. 步骤三(对h(x)赋值获得不等式):设x2>x1,则ex2-ex1-x2+x1>0. 步骤四(借助对数平均不等式放缩):设定问题(2)待证不等式形式为x1x2<λ2,得到|λ|(lnx2-lnx1)>x2-x1. 步骤五(构造题设函数f(x)):将ex2-ex1-x2+x1>0与|λ|(lnx2-lnx1)>x2-x1相减,得到F(x1)≈F(x2),其中F(x)=ex-|λ|lnx,由此可设定题设函数f(x)=ex-alnx. 步骤六(进行合理设问):问题(1)设定考查导数的几何意义,故问题(1)要求学生求解函数g(x)=f(x)+alnx在x=0处的切线与坐标轴所围成的三角形的面积.问题(2)设定为:若∃x1,x2∈(0,+∞),x1≠x2,使得f(x1)=f(x2),求证:x1x2 综合上述命制过程,得到如下新题: 题5 已知函数f(x)=ex-alnx. (1)当a=1时,求函数f(x)在x=1处的切线与坐标轴所围成的三角形的面积; (2)若∃x1,x2∈(0,+∞),x1≠x2,使得f(x1)=f(x2),求证:x1x2 评注5:由上述两道试题的命制过程观之,u(x)的表达式决定了最终题设函数f(x)形式.题4-5所取的u(x)都较为简单,所以命制出来的两道试题的难度都较为适中,若增加选取的u(x)的表达式的复杂度,可命制出难度更大的试题,限于篇幅,此处不再举例说明. 解题是数学活动的基本形式和主要内容,数学学习离不开解题学习,故数学教学离不开解题教学.那么,在解题教学中如何培养学生的数学核心素养? 在试题求解分析环节,学生经历了“从数量与数量关系中抽象出变量与变量之间的关系,从事物的具体背景中抽象出一般规律和结构,进而“选择运算方法,设计运算程序”,最后“从一些事实和命题出发,依据逻辑规则推出一个命题”的过程,无疑,数学抽象、数学运算、逻辑推理等素养得到了较好的培养和发展. 在命题手法剖析环节,学生经历了“从数量与数量关系中抽象出变量与变量之间的关系,从事物的具体背景中抽象出一般规律和结构”,进而“从数学的视角发现问题、提出问题,收集数据,整理数据,提取信息”的过程,无疑,数学抽象、数据分析等核心素养得到了较好的培养和发展. 在试题再命制环节,学生经历了“分析问题、建立模型,确定参数、计算求解,检验结果、改进模型”的过程,无疑,数学建模等核心素养得到了较好的培养和发展.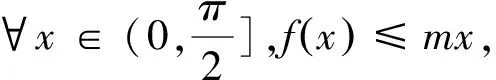
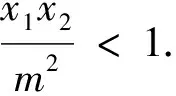
2、拨开云雾见天日——分析求解过程
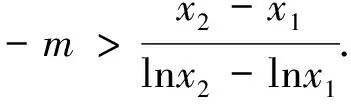


3、打破砂锅问到底——探寻命题手法
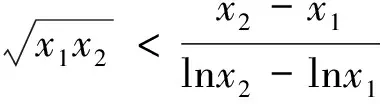
4、横看成岭侧成峰——命制不同试题


5、一叶落知天下秋——提升核心素养

