基于VMD-BiLSTM-ATT预测模型的碳中和指数量化投资研究

欧阳资生　唐伯聪

摘要：碳中和指数是落实碳中和战略、推动经济绿色转型的重要工具和载体，准确预测碳中和指数可以为相关政策的实施提供依据，吸引投资者参与碳中和市场并获取收益。因此，本文提出了一种融合数据分解重构和注意力机制的深度学习预测模型——VMD-BiLSTM-ATT模型，并将其运用到碳中和指数的预测与应用中。具体而言，研究分为三个部分，一是通过计算四个误差评价指标验证本文模型具备最佳预测性能，二是为获取更高的预测精度对模型超参数进行调整得到最优超参数组合，三是以六个投资评价指标为标准衡量模型的投资应用价值。实证结果表明，在预测性能方面， VMD-BiLSTM-ATT模型优于所有基准模型，且经过超参数调整后，模型预测性能更佳；在量化投资应用方面，基于本文模型的碳中和指数投资策略获得的投资绩效远远优于持有期相同的碳中和指数和沪深300指数的投资绩效，并且超参数的调整能在此基础上进一步提升投资绩效，证明了本文模型在量化投资方面具有良好的应用价值。

关键词：碳中和指数；深度学习；变分模态分解；注意力机制

中图分类号：F832.5         文献标识码：A              文章编号：1007-0753（2023）10-0075-16

一、引言

工业革命以来，化石能源的消耗使得空气中CO2含量逐渐增加，导致全球气候变暖并引发一系列环境问题，如极端天气和自然灾害增多、作物生长环境受影响而导致产量下降、土地沙漠化、冰川消融及海平面上升等。为实现气候治理，《巴黎协定》提议把全球平均气温较工业化前水平升高控制在2 ℃之内，并为把升温控制在1.5 ℃之内而努力。截至2021年底，全球已有 136个国家提出了“碳中和”承诺。有关气候问题，习近平主席强调“气候变化是全球性挑战，任何一国都无法置身事外”，并于2020年正式提出“双碳”目标。“双碳”目标不仅符合国家可持续发展战略的要求，推动了生态文明建设和高质量发展，而且展现出中国主动承担应对全球气候变化责任的大国担当。“双碳”目标提出后，我国政府陆续出台相关的碳减排政策，积极引导资金流入碳中和市场，从而推进经济绿色转型发展。碳中和指数既是反映碳中和市场变化情况的客观评价指标，又是资本市场落实碳中和战略、推动经济绿色转型的重要工具和载体，准确预测碳中和指数在碳中和研究中就显得尤为重要。从政府角度看，它可以帮助政府提前预知未来市场发展趋势，为相关政策实施提供参考；从投资者和市场角度看，先进的预测模型一方面可以吸引投资者参与碳中和市场获取收益，另一方面随着投资额的增加为碳中和市场注入资金，助力“双碳”目标的实现。

二、文献综述

目前来看，碳中和相关研究主要分为以下三个方面：一是绿色金融对碳排放的影响。绿色金融是国家实现碳中和环境治理的核心，在碳市场的发展中具有舉足轻重的地位。Saeed Meo和 Karim（2022）考察了包含英国、美国和日本在内的十大支持绿色金融的经济体，发现绿色金融是减少碳排放的最佳金融策略。由于国家间的市场状况不同，绿色金融对碳排放虽然呈现负向影响，但不同分位数之间的影响程度是不同的。因此，绿色金融发展应结合具体国情，积极探索有中国特色的道路。二是碳排放权交易市场的研究与预测。碳排放权交易市场是实现碳中和目标的核心政策工具，是利用市场机制实现最低减排成本的重要制度创新。市场的完善离不开对价格的研究，从传统的计量模型方法到人工智能预测技术，碳价格预测模型精度不断提升，然而碳价格变动是非线性且复杂的。目前来看，预测效果较优异的模型还是加入时间序列分解的预测模型，如Rezaei等（2021）使用二次分解的机器学习模型并证明了模型的有效性。三是碳中和的实现途径。碳中和作为我国可持续发展的纲领性目标，其实现路径也值得仔细探讨。张浩楠等（2022）总结了碳中和实现的两条路径，分别是以可再生能源为基础的“零碳”途径，以及依靠化石能源脱碳化处理的“净零”途径，但两者之间存在一定的冲突，需要进一步讨论两者的系统可塑性、经济适用性和减碳潜力等。总的来看，与西方国家碳排放集中在消费端相比，我国碳排放主要集中在生产端，因此应当坚持采取“受益者付费”的消费端责任原则，走中国特色碳中和道路，而非盲目学习西方模式。

以上研究涉及公司层面的绿色融资与碳排放的关系、市场层面的碳排放权交易价格预测以及宏观层面的碳中和实现路径。碳中和指数由于发布时间较晚，国内外相关研究目前停留在指数的构建与变动趋势分析上（陈梦月等，2022；孙翊，2022）。不足的是，历史的变动分析远远不能满足投资者、市场和政府的需求，而对指数变化趋势的预测分析更能带来实际的价值，例如，买卖指数后的收益预测、政策实施后的效果预测以及经济大环境的变化趋势预测等。

在早期，由于机器学习技术不够普及，金融时间预测研究多采用传统的计量预测模型，如移动平均自回归模型（ARIMA）、广义自回归条件异方差模型（GARCH）等（惠晓峰等，2003）。传统的计量模型虽简洁实用，但其仅适用于较平稳的时间序列数据，对于复杂数据的预测效果较差。随着计算机技术的不断发展，虽然传统的计量模型仍占有一席之地，如张贵生等（2016）曾运用基于微分信息的ARMAD-GARCH模型对五种不同市场的指数进行预测，预测结果具备一定的准确性和稳定性，但在多数情况下传统模型已不能满足研究者对预测精度的要求。基于计算机技术的深度学习网络模型开始进入学者的视野，如杨刚等（2021）的研究表明ELM神经网络较ARMA模型预测精度有显著提高，可为气温衍生品的定价奠定基础。在预测研究中，许多学者的研究结果都表明了挖掘时间序列数据长期依赖关系的循环神经网络相比于传统计量模型和前馈神经网络模型更具优势（Chandra等，2021；Yang等，2023）。循环神经网络模型中，传统循环神经网络（RNN）由于容易陷入梯度消失和梯度爆炸而较少在预测研究中使用。Shen等（2018）在对恒生指数、德国股票指数和标准普尔500指数的预测中，证明了门控循环网络模型（GRU）的预测精度优于传统循环神经网络（RNN）和支持向量机模型（SVM）。长短期记忆模型（LSTM）由于其强泛化能力在时间序列预测中备受青睐。杨青和王晨蔚（2019）通过全球30个指数数据研究了LSTM模型的泛用性、准确性和稳定性，认为其在金融预测中有广阔的应用前景。欧阳资生等（2022）为提高模型的预测精度，将LSTM纳入金融风险预警体系，发现LSTM的引入有利于构建科学的风险检测和预警机制。双向长短期记忆模型（BiLSTM）与前面的模型相比，其优势在于能够双向读取序列信息，从而在预测中更充分地利用信息。Barua 和 Sharma（2022）对LSTM和BiLSTM两个模型进行了对比研究，从评价指标结果来看BiLSTM模型的预测性能更加优越。

随着研究数据的复杂化和多样化，波动大的复杂数据想要取得与较平稳数据相近的预测结果是十分困难的，而物理学中的信号分解理论正好为这个难题提供了一个可行的解决方法。信号分解理论通过将成分复杂的原数据分解成一系列规则的子序列，然后对各子序列分别进行预测，从而达到提升模型预测精度的目的。金融时间序列分析中常见的信号分解理论有小波分解（WT）（Chang等，2019）、经验模态分解（EMD）（Wang等，2020）和变分模态分解（VMD）（Huang等，2021）等。WT分解和EMD分解都存在一定的局限性，前者需要主观设计基函数，后者则是容易产生模态混叠，相比之下VMD分解具有不容易产生模态混叠和自主选择分解子序列个数的两大优势，因此常运用于时间序列分析预测中。Liu等（2020）将VMD分解与长短期记忆模型（LSTM）相结合，构建了预测模型并与其他六种最先进的方法进行比较；结果表明，该模型对有色金属价格预测具有较好的效果。

信号分解理论的引入虽然使得模型在精度和稳定性方面有了极大提升，但仍需合理利用计算资源，即将计算能力更多地用于对预测有帮助的信息中，减少无关信息的干扰。注意力机制便具有这项能力，能在计算能力有限的情况下，依据对预测结果的贡献度不同给信息赋予不同权重，提升预测效率。Qiu等（2020）通过研究标准普尔500综合股价指数、道琼斯工业平均指数和恒生指数等数据发现，在LSTM模型中加入注意力机制会使得模型的可决系数均高于94%且均方误差低于0.05。Ouyang等（2021）在系统性风险指标的预测中也证实了各风险指标的预测精度都随着注意力机制的加入而提升。Abbasimehr和Paki（2022）的研究也同样表明注意力机制的引入能够显著提高模型的预测性能。

前文主要介绍了预测模型的发展以及如何构建预测模型才能提升预测性能，但预测只是方法与过程，最终的落脚点在于模型的应用。从近些年的研究来看，机器学习预测模型在金融领域的应用屡见不鲜。张鹏等（2023）认为优质股票的选择是投资组合获益的基石，从而提出了基于机器学习方法选股和以均值-下半方差构建投资组合的XGBoost+MSV模型，该模型在收益和风险指标上均优于其他模型。Cipiloglu等（2020）则利用LSTM模型预测未来收益方向，然后将这些预测用于计算投资组合权重，通过与常见的投资组合构造策略比较分析得出，融入LSTM模型后预测将会改善投资组合的绩效。但是机器学习预测模型在投资领域的应用远不止于此，先进的预测方法以及与之结合的更丰富的投资策略构造仍待探索和发掘。

在前文研究的基礎上，本文从改进预测方法的角度入手，提出预测更为准确的VMD-BiLSTM-ATT模型，并通过其在碳中和指数的投资应用来评判模型的应用价值。本文的边际贡献在于：一是扩展了碳中和指数相关研究，将研究领域从碳中和指数的构建和变动趋势分析，延伸到碳中和指数的预测以及构造投资策略进行投资应用分析；二是为预测研究提供了新的预测方法。本文所提出的模型充分结合了数据分解重构、注意力机制和深度学习三大结构的优势。在实证研究中，通过与前人提出的不同架构模型进行对比分析发现，本文模型在各项误差指标评价中都具备最优预测性能。

三、模型构建与评价指标

（一）变分模态分解

Dragomiretskiy等（2014）提出了一个完全非递归的分解模型VMD（Variational Mode Decomposition），即变分模态分解。VMD模型通过寻找一组本征模态函数（Intrinsic Mode Function，IMF）和它们各自的中心频率来共同再现输入信号。与传统信号分解算法相比，VMD不仅拥有自主选择模态个数的优点，而且克服了EMD方法存在端点效应和模态分量混叠的问题，并具有更坚实的数学理论基础，可以降低复杂度高和非线性强的时间序列的非平稳性，分解获得包含多个不同频率尺度且相对平稳的子序列，适用于非平稳性的序列。VMD的核心思想是构建和求解变分问题。

其中，tanh表示正切双曲函数，σ表示sigmoid函数。

因此，在LSTM模型的基础上构建的BiLSTM模型单元结构如图2所示。

输入序列分别以正序和逆序输入2个LSTM神经网络进行特征提取，正序输入生成对应的输出值h→ = {h→1， h→2，…，h→n }；同样地，逆序输入也会生成对应的输出值h← = {h←1， h←2，…， h←n }。最后将正序与逆序对应的输出值进行拼接得到BiLSTM的输出值h = {h1， h2，…， hn }。

（三）注意力机制

神经网络中的注意力机制（Attention Mechanism，ATT）是指在计算能力有限的情况下，将计算资源分配给更重要任务的一种资源分配机制。通过引入注意力机制，可以在众多的输入信息中聚焦对当前任务更为关键的信息，降低对其他信息的关注度，提高任务处理的效率和准确性。在实际应用中，注意力机制通常分为软注意力机制和硬注意力机制。软注意力机制是指在学习所有数据时计算每个数据的权重，然后进行相应的加权平均。相对地，硬注意力机制的权重只能是0或1。本文模型采用软注意力机制来处理神经网络的问题，在模型训练过程中，依据不同特征赋予碳中和指数预测的贡献率不同的注意力权重。图3展示了注意力机制的网络结构。

对于一个i维的特征输入，通过密集层生成对应的特征隐藏输出值S = {s1，s2，s3，…，si}；然后该隐藏输出值通过softmax函数转化为权重和为1的特征权重向量A = {α1，α2，α3，…，αi}；由于整个变换中并未改变特征的维度，最后可以将每个输入特征与对应的特征权重相乘，从而得到注意力层的最终输出结果。

（四）VMD-BiLSTM-ATT模型

在前文三个模型的基础上，集成各模型的优点，通过对模型的有效组合，提出了预测更为精确的VMD-BiLSTM-ATT模型。模型的具体组成结构如图4所示。

VMD-BiLSTM-ATT模型的原理是对数据的分解、预测和重构。先是分解以降低数据的复杂度，将复杂数据的预测问题转化为对简单分量数据的预测问题，然后将各分量分别输入BiLSTM-ATT模型预测得到分量预测结果，最后重构分量预测结果，加总得到最终预测值。模型的具体实现步骤如下：

1.将碳中和指数输入至VMD模型中进行数据分解，得到各本征模态函数IMF = {IMF1， IMF2， …， IMFn}；

2.将分解的各分量输入融合注意力机制的BiLSTM-ATT模型，先是将各分量输入至BiLSTM模型得到BiLSTM层输出结果，再通过注意力层提取得到注意力加权特征；

3.从上一步获取的特征输入至Dense层得到各IMF分量的预测结果Prediction={Predicton1，Pred-icton2 ，… ， Predictonn}；

4.最后对各分量预测值加总获得碳中和指数的最终预测值。

（五）误差评价指标

平均绝对误差（MAE）：衡量预测值与真实值之间的平均绝对误差，MAE越小表示模型越好。

四、碳中和指数量化投资模型选择

（一）数据来源与描述性统计分析

本文从中证指数官网获取2017年6月30日—2022年12月31日的SEEE碳中和指数收盘价数据，数据中的前80%用作训练集训练模型，后20%数据用作测试集验证模型的性能。碳中和指数共计100只样本股，以2017年6月30日为基期，以

1 000点为基点。样本股筛选基于碳中和概念股过去一年成交金额排名的前90%，再剔除其中ESG得分后 10%的股票。样本股分为深度低碳（清洁能源与储能、绿色交通、减碳和固碳技术等）和高碳减排（火电、钢铁、建材、有色金属、化工、建筑等）两个领域并分别赋予不同权重。其中，2022年深度低碳领域贡献度为 66.47%， 高碳减排领域贡献度为 33.53%。由此可见，碳中和指数构成科学合理，能充分反映我国碳中和市场的整体表现。碳中和指数时间序列图及描述性统计表见图5和表1。

从图5可以看到，整体上碳中和指数波动较大。碳中和指数较大的变动往往与国家政策的提出相关，2017年6月至2020年9月，我国在碳减排方面的政策和举措力度较小，碳中和指数的变动较为平稳。2020年9月22日，习近平主席在第七十五届联合国大会上提出“双碳”目标，一系列政策措施在其后两年内相继颁布，碳中和指数进入高速上涨期。2021年末，碳中和指数到达顶峰，此时碳中和指数已经居于高位。2022年一季度指数开始下跌。2022年3月，《“十四五”东西部科技合作实施方案》颁布，指数再次上涨但幅度远不及高速上涨期。之后指数虽有波动，但逐渐趋于稳定。

表1展示了碳中和指数的7个数据特征，从数据的最大值、最小值、中位数、均值及标准差并结合图5分析可知碳中和指数数据波动较大，这意味着如果不采用数据分解而直接对指数进行预测，准确率较难达到预测要求。从数据的偏度和峰度分析可知，碳中和指数呈现正偏态且分布较为平缓。

（二）模型比较分析

本节通过比较不同深度学习模型及其组合模型以验证所构建模型的有效性。本文使用前6个交易日的碳中和指数收盘价作为数据的输入特征，后1个交易日收盘价作为输出值（即预测结果），利用单位交易日滑动窗口获得一系列输入特征与输出值。首先，在训练集中通过优化预测值与真实值的距离来训练深度学习模型；随后，在测试集中利用训练好的模型获取碳中和指数收盘价的预测值；最后，由真实值和预测值计算得到四个误差评价指标，用于各深度学习模型性能的比较分析。模型的相关超参数设置如表2所示。

完成相关超参数设置后，将所有模型分为三部分，分别是基础的循环神经网络模型、加入VMD分解的循环神经网络模型及融合VMD分解和注意力机制的循环神经网络模型，并从四个误差评价指标上分析不同模型的性能，不同模型间的比较结果如表3所示。在第一部分中，本文比较了四个循环神经网络模型（RNN、GRU、LSTM和BiLSTM）。可以看到，BiLSTM模型在四个误差评价指标上都具有最优的结果，而RNN虽具备信息记忆能力，但对信息的处理能力不足，模型性能最差。因此，在循环神经网络的选择上，优先选择BiLSTM并在此基础上融入VMD分解和注意力机制。

在第二部分中，通过加入VMD分解，所有模型都获得了极大的预测性能提升，其中VMD-GRU模型提升幅度最大，且性能接近于VMD-BiLSTM模型，但加入VMD分解的BiLSTM模型在所有误差评价指标上依然优于其他模型。VMD分解加入后，BiLSTM模型的MAE、RMSE和MAPE分别下降了7.738 6、11.745 3和0.004，R2提升了0.020 8。

第三部分在第二部分的基础上引入了注意力机制，通过对特征的注意力加权来提升模型的性能。可以看到，注意力机制的引入对性能的提升虽不如VMD分解，但也在一定程度上提升了各模型的性能。VMD-BiLSTM-ATT模型与所有基准模型相比，仍具备最优的预测性能，其MAE、RMSE、MAPE和R2分别为15.953 0、19.067 3、0.008 2和0.988 1。

（三）模型超參数优化

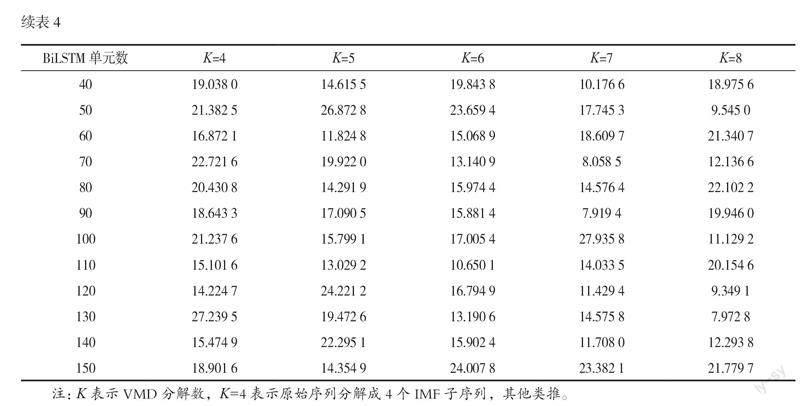
在深度学习的算法中，超参数作为不通过训练优化的提前进行设置的一种参数类型（如神经网络单元数等），其选择是训练深度学习模型时必不可少的过程，并且会直接影响模型的训练速度和质量。为进一步提高模型的预测精度，本文将对模型中最重要的两个超参数（VMD分解数和BiLSTM单元数）进行调整。通过对比不同超参数组合下的误差评价指标，选择出最优的超参数组合。表4—表7分别展示了MAE、RMSE、MAPE和R2在不同超参数组合下的值。

如表4—表7所示，各误差评价指标反映的是模型在不同角度上的预测性能，故在不同超参数组合下，MAE、RMSE、MAPE和R2四个误差评价指标的最优值会产生相应的变化。其中MAE和MAPE都在K=7和BiLSTM单元数为90时取得最低值，分别为7.919 4和0.004 0，而RMSE和R2在参数组合为K=8和BiLSTM单元数为130时分别达到最低值10.068 0和最高值0.996 7（R2反映的是模型的拟合效果，值越大代表拟合效果越好）。总体来说，两组超参数组合的性能差距并不大，但考虑到VMD分解数和BiLSTM单元数的增加会显著提高模型预测所需的时间，经过综合考虑后确定本文模型的最优超参数组合为K=7和BiLSTM单元数为90。

为了证明模型在超参数调整后依然具备最优性，本文基于调整后的超参数（VMD分解数变为K=7和BiLSTM单元数变为90，其余超参数不做改变）重新训练本文模型与各基准模型，并将它们在测试集上的误差评价指标结果列于表8中。

如表8所示，经过超参数优化的各模型预测性能总体趋势基本与超参数调整前一致：（1）在基础的循环神经网络模型中，BiLSTM依然具有最佳预测性能；（2）加入VMD分解的循环神经网络模型显著优于基础的循环神经网络模型；（3）在VMD分解的基础上，注意力机制的引入能够进一步提升模型的性能；（4）本文模型，即VMD-BiLSTM-ATT模型依然具备最优预测性能。

模型在总体趋势上与超参数调整前保持一致，也从一定程度上证明了模型的鲁棒性。从表8中能够明显看到超参数调整使得大多数模型得到了优化，MAE、RMSE和MAPE相较超参数调整前都有一定程度的下降，同样地R2也得到了提升。为了更好地反映误差评价指标的变化情况，本文对超参数调整前后误差评价指标的变化进行了分析，结果见表9。

如表9所示，大多数模型的性能都在超参数调整后得到了提升，其中基础循环神经网络模型的提升幅度较小，甚至性能有所下降，但随着VMD分解和注意力机制的逐渐加入，各模型的性能提升幅度显著增加。从各部分来看：在第一部分中，GRU和BiLSTM的性能得到了小幅度提升，但RNN和LSTM的性能下降；在第二部分中，除VMD-RNN的性能大幅度下降外，其余三个模型的性能皆得到了大幅提升；而在第三部分中，所有模型的性能都在参数调整后得到了大幅度提升，尤其是VMD-BiLSTM-ATT的误差评价指标MAE、RMSE和MAPE都下降了近50%，同时R2提升了0.85%。上述结果证明了VMD分解和注意力机制在深度学习预测领域的重要性。

五、量化投资应用分析

模型的预测性能是应用的保证，模型的应用则是预测的最终目的，本节将利用VMD-BiLSTM-ATT模型的预测结果来构造投资策略，根据模型在六个投资评价指标上的表现讨论模型的应用价值。具体的投资策略构造过程如下：

首先，运用已训练好的VMD-BiLSTM-ATT模型在测试集中预测的碳中和指数收盘价预测值计算碳中和指数预测收益率，第i天碳中和指数预测收益率R ?i的计算公式如下：

R ?i = ln（ p ? i /pi-1）                                                 （17）

其中， p ? i为碳中和指数在第i天的预测收盘价，pi-1为碳中和指数在第i-1天的真实收盘价。然后依据预测结果将碳中和指数价格运动分为“上涨”（up）和“下跌”（down）两类，其定义如下：

（18）

本文设置以下交易策略：在碳中和指数预测结果为“上涨”时买入或持有碳中和指数，在碳中和指数预测结果为“下跌”时卖出或不持有碳中和指数。为了实验的简单性和公平性，忽略所有比较方法的交易成本。

通过本文提出的VMD-BiLSTM-ATT模型在测试集上的预测结果，采取上述投资策略买卖指数，并依据预测结果计算出年化收益率、夏普比率、胜率、盈亏比、VaR和ES共六类投资评价指标来检验模型用于量化投资的有效性。具体投资评价指标计算公式如表10所示，各投资评价指标的具体计算值如表11所示。

表11展示了四列投资评价指标，其中超参数优化后和超参数优化前的投资评价指标采取本文模型的碳中和指数投资策略计算所得，而碳中和指数和沪深300指数的投资评价指标则是采取消极投资策略（即简单购买持有）计算得出。通过对比采用本文投资策略的超参数优化后、超参数优化前以及持有期相同的碳中和指数和沪深300指数的六项投资评价指标可得：未使用本文模型时，持有碳中和指数相较沪深300指数而言，承擔了更高的风险却享有更低的收益，即采取消极投资策略参与碳中和市场投资并不能从中获益。反观采取本文模型预测的投资策略，其经超参数优化后的年化收益率、夏普比率、胜率以及盈亏比分别为421.32%、1.064 0、87.27%和5.788 5，均高于超参数优化前，且比简单购买持有碳中和指数和沪深300指数的年化收益率分别高出459.97个百分点和451.73个百分点、夏普比率高出1.136 3和1.137 0、胜率高出38.77个百分点和40.28个百分点，盈亏比高出4.900 5和4.848 9；同时，超参数优化后的风险指标度量值VaR和ES分别为33.85%和42.45%，也小于超参数优化前、碳中和指数和沪深300指数。总而言之，超参数优化不仅能够优化模型误差，也能提高模型的投资应用能力，采取VMD-BiLSTM-ATT预测模型的投资策略比持有碳中和指数和沪深300指数收益更高、风险更低，本文模型在投资应用方面具有良好的实用价值。

六、结论

本文将信号分解理论、注意力机制和深度学习网络三者有机结合，提出了一种混合预测模型——VMD-BiLSTM-ATT模型。具体来说，模型分为以下三个步骤：步骤一，利用VMD分解得到各子序列，降低原序列的预测难度；步骤二，通过BiLSTM模型的双向处理获得子序列的特征输出，然后引入注意力层依据各特征的重要程度对其进行加权；步骤三，将特征输入密集层获得子序列预测结果，子序列预测值加总获得最终预测值。

在预测模型评价上，本文依据MAE、RMSE、MAPE和R2四个误差评价指标对比分析了VMD分解和注意力机制的加入是否能够提升循环神经网络模型的预测性能。结果显示，VMD分解能够降低序列复杂度，从而大幅度提升模型的预测精度；注意力机制的加入效果虽不如VMD分解，但也能在一定程度上降低模型误差。VMD-BiLSTM-ATT模型在四个误差评价指标上均为最优，其值分别为15.953 0、19.067 3、0.008 2和0.988 1。在此基础上，对模型的两个重要超参数（VMD分解数和BiLSTM单元数）进行超参数调整来寻找最优超参数组合，结果发现：当VMD分解数K=7和BiLSTM单元数为90时，模型在总体趋势上与超参数调整前保持一致，大多数模型的预测性能都在超参数调整后得到了提升，且本文模型提升幅度最高，MAE、RMSE和MAPE都下降了近50%，同时R2提升了0.85%。这也进一步说明了模型的有效性和鲁棒性。

在預测模型的投资应用价值上，本文进行了投资策略的构造并根据模型预测结果计算测试集内超参数优化后、超参数优化前和持有期相同的碳中和指数和沪深300指数的六个投资评价指标。实证结果说明，超参数优化后的VMD-BiLSTM-ATT模型不仅能够降低模型误差，而且提高了模型的投资应用能力，采用本文模型的量化投资结果具有更高的收益和更低的风险，年化收益率、夏普比率、胜率、盈亏比、VaR和ES分别为421.32%、1.064 0、87.27%、5.788 5、33.85%和42.45%。由此可见，本文模型在投资领域中具有良好的应用价值。

参考文献：

[1] SAEED MEO M， KARIM M Z A. The role of green finance in reducing CO2 emissions：An empirical analysis[J]. Borsa Istanbul Review， 2022，22（01）：169-178．

[2] REZAEI H， FAALJOU H， MANSOURFAR G. Stock price prediction using deep learning and frequency decomposition[J]. Expert Systems with Applications， 2021， 169：114332．

[3]张浩楠，申融容，张兴平，等.中国碳中和目标内涵与实现路径综述[J].气候变化研究进展，2022，18（02）：240-252.

[4]陈梦月，姚惠芳.碳中和股价指数的构建与应用[J].中国林业经济，2022（02）：97-100.

[5]孙翊.碳中和指数构建与指数波动研究[J].中国林业经济，2022（05）：92-94.

[6]惠晓峰，柳鸿生，胡伟，等.基于时间序列GARCH模型的人民币汇率预测[J].金融研究，2003（05）：99-105.

[7]张贵生，张信东.基于微分信息的ARMAD-GARCH股价预测模型[J].系统工程理论与实践，2016，36（05）：1136-1145.

[8]杨刚，王文卓.碳中和背景下气温衍生品定价研究——基于ELM神经网络方法[J].金融发展研究，2021（08）：66-73.

[9] CHANDRA R，GOYAL S，GUPTA R．Evaluation of deep learning models for multi-step ahead time series prediction[J]．IEEE Access，2021，9：83105-83123．

[10] YANG P， WANG Y L， ZHAO S Y， et al. A carbon price hybrid forecasting model based on data multi-scale decomposition and machine learning[J]．Environmental Science and Pollution Research，2023，30（2）：3252-3269．

[11] SHEN G Z，TAN Q P，ZHANG H Y，et al．Deep learning with gated recurrent unit networks for financial sequence predictions[J]．Procedia Computer Science，2018，131：895-903.

[12]杨青，王晨蔚.基于深度学习LSTM神经网络的全球股票指数预测研究[J].统计研究，2019，36（03）：65-77.

[13]欧阳资生，路敏，周学伟.基于TVP-VAR-LSTM模型的中国金融业风险溢出与预警研究[J].统计与信息论坛，2022，37（10）：53-64.

[14] BARUA R，SHARMA A K.Dynamic Black Litterman portfolios with views derived via CNN-BiLSTM predictions[J]．Finance Research Letters，2022，49：103111.

[15] CHANG Z H，ZHANG Y，CHEN W B.Electricity price prediction based on hybrid model of Adam optimized LSTM neural network and wavelet transform[J].Energy，2019，187：115804．

[16] WANG B，WANG J.Energy futures and spots prices forecasting by hybrid SW-GRU with EMD and error evaluation[J].Energy Economics，2020，90：104827.

[17] HUANG Y S，DENG Y.A new crude oil price forecasting model based on variational mode decomposition[J].Knowledge-Based Systems，2021，213：106669．

[18] LIU Y S，YANG C H，HUANG K K，et al.Non-ferrous metals price forecasting based on variational mode decomposition and LSTM network[J].Knowledge-Based Systems，2020，188：105006．

[19] QIU J Y，WANG B，ZHOU C J.Forecasting stock prices with long-short term memory neural network based on attention mechanism[J].PLoS One，2020，15（01）：e0227222．

[20] OUYANG Z S，YANG X T，LAI Y Z.Systemic financial risk early warning of financial market in China using Attention-LSTM model[J].The North American Journal of Economics and Finance，2021，56：101383．

[21] ABBASIMEHR H，PAKI R.Improving time series forecasting using LSTM and attention models[J].Journal of Ambient Intelligence and Humanized Computing，2022，13（1）：673-691．

[22]张鹏，党世力，黄梅雨.基于机器学习预测股票收益率的两步骤M-SV投资组合优化[J/OL].中国管理科学：1-14[2023-10-19].DOI：10.16381/j.cnki.issn1003-207x.2021.2308.

[23]CIPILOGLU YILDIZ Z，YILDIZ S B.A portfolio construction framework using LSTM-based stock markets forecasting[J].International Journal of Finance & Economics ，2020，27（02）：2356-2366．

[24] DRAGOMIRETSKIY K，ZOSSO D.Variational mode decomposition[J].IEEE Transactions on Signal Processing，2014，62（03）：531-544．

[25] Hochreiter S， Schmidhuber J. Long short-term memory[J]. Neural computation， 1997， 9（08）： 1735-1780.

[26]李斌，林彦，唐闻轩.ML-TEA：一套基于机器学习和技术分析的量化投资算法[J].系统工程理论与实践，2017，37（05）：1089-1100．

[27] WEN F H，WU N，GONG X.China's carbon emissions

trading and stock returns[J].Energy Economics，2020，86：

104627．

[28]唐曉彬，董曼茹，张瑞.基于机器学习LSTM&US模型的消费者信心指数预测研究[J].统计研究，2020，37（07）： 104-115.

[29]李沐勋.基于机器学习算法的信用风险量化模型研究[J].金融经济，2023（04）：75-83．

[30]  SEZER O B，GUDELEK M U， OZBAYOGLU A. Financial time series forecasting with deep learning：A systematic literature review： 2005-2019 [J]. Applied Soft Computing ，2020，90.

[31]欧阳红兵，黄亢，闫洪举.基于LSTM神经网络的金融时间序列预测[J].中国管理科学，2020，28（04）：27-35.

（责任编辑：唐诗柔）

Quantifying Carbon Neutrality Investment Research

Based on VMD-BiLSTM-ATT Forecasting Model

OUYANG Zisheng， TANG Bocong

（Business School， Hunan Normal University）

Abstract： The carbon neutrality index is an important tool and carrier for implementing the carbon neutrality strategy and promoting the green transformation of the economy. Accurately predicting the carbon neutrality index can provide a basis for the implementation of related policies and attract investors to participate in the carbon neutrality market and obtain returns. Therefore， this paper proposes a deep learning forecasting model that integrates data decomposition reconstruction and attention mechanism， the VMD-BiLSTM-ATT model， and applies it to the prediction and application of the carbon neutrality index. Specifically， the research is divided into three parts： first， four error evaluation indicators are used to verify that this model has the best predictive performance; second， the model hyperparameters are adjusted to obtain the optimal hyperparameter combination for higher prediction accuracy; third， six investment evaluation indicators are used as criteria to measure the investment application value of the model. Empirical results show that in terms of predictive performance， the VMD-BiLSTM-ATT model outperforms all benchmark models， and the predictive performance of the model is better after hyperparameter tuning; in terms of quantitative investment applications， the carbon neutrality index investment strategy based on this model achieves much better investment performance than the carbon neutrality index and Shanghai and Shenzhen 300 index with the same holding period， and hyperparameter tuning can further improve investment performance on this basis， proving that the model has good application value in quantitative investment.

Keywords： Carbon neutrality index; Deep learning; Variational mode decomposition; Attention mechanism

收稿日期： 2023-07-19

作者简介：欧阳资生，教授，博士生导师，湖南师范大学商学院，研究方向为金融风险管理与金融科技。

唐伯聪，硕士研究生，湖南师范大学商学院，研究方向为金融科技。

基金项目：国家社会科学基金项目“中国金融市场输入性风险测度与预警研究”（23BTJ043）。