基于集成算法的信用债违约预测模型及其影响因素研究

郑怡昕　王重仁

摘要：本文选取2014—2021年的信用债作为研究对象，以单一算法（逻辑回归、高斯朴素贝叶斯、支持向量机和伯努利朴素贝叶斯）分别构建Bagging和Stacking集成学习模型，并将其与单一算法以及传统方法（KMV模型）进行对比，探讨如何提高信用债违约预测精度，证明Bagging集成算法的可靠性，还通过SHAP可解释算法研究信用债违约中的重要指标。实证结果显示，四种单一机器学习模型在预测准确率上优于传统KMV模型；进一步对机器学习模型进行集成，发现同质集成算法在提高预测性能方面不如异质集成算法，且Bagging异质集成算法的预测准确率优于Stacking异质集成算法。将性能最好的Bagging异质集成算法与SHAP可解释算法结合，得到对识别信用债违约具有重要价值的9个指标，分别是违约前债项评级、违约前主体评级、交易所、净资产收益率、债券类型、企业性质、财务费用、总资产增长率以及第一大股东持股比例，关键指标的识别对信用债违约预测具有指导意义。

关键词：信用债违约；风险预警；Bagging集成算法；Stacking集成算法；SHAP可解释算法

中图分类号： F832.5      文献标识码：A           文章编号：1007-0753（2023）10-0018-10

一、引言

信用债作为企业直接融资的重要工具，在保障实体经济健康发展，解决融资难、融资贵问题上发挥着重要作用。随着时间的推移，债券融资的发展空间逐渐扩大。然而通过分析2015—2021年信用债违约情况可以发现，随着市场规模的扩大，信用风险问题日益凸显。2015年受产能过剩的影响，上游周期行业的违约事件频繁发生，使得违约主体数量大幅上升。2018年随着去杠杆政策的出台，民营企业违约现象频发，引发了第二波违约潮，2019年违约主体数量达到峰值。从违约金额来看，第二波违约潮在2018年后对市场的冲击和影响远超过2015年开始的第一波违约潮。随着信用债市场的快速整顿，从2020年开始，违约主体数量有所下降，2021年的首次违约主体数量为16家，较上年减少14家，2020—2021年间违约金额也开始回落（杜渐和周冠男，2022）。

2021年的信用债市场处于经历“永煤事件”后的修复期，整体上信用债违约事件有所减少，但在违约主体的评级、性质、行业和地区分布等方面也出现了一些新变化。首先，各行业中的违约主体呈现出不同的特点。例如，受到宏观经济形势影响较大的传统制造业企业，面临着生产成本上升、市场竞争加剧等压力，违约风险相对较高。与此同时，新兴科技和绿色能源等领域的企业由于创新性强、市场需求大，违约风险相对较低。其次，地区间的经济发展不平衡也在一定程度上影响着信用债市场的稳定性。发达地区的企业普遍具有较强的抗风险能力，而欠发达地区的企业则更容易受到地区性经济波动的影响，违约风险较高。

此外，信用债市场的政策环境也发生了一些变化。监管机构加大了对信用风险的监管力度，提高了信用债的发行门槛，加强了信息披露要求，这在一定程度上提高了市场的透明度，但也使得部分中小企業融资难度增加，这可能增加他们的违约风险。同时，货币政策的变化也直接影响了市场流动性，对信用债违约形成了一定的影响。综上所述，了解当前信用债市场的变化，对于预测潜在的违约风险、制定相应的风险管理策略以及维护市场的稳定性具有重要意义。

二、文献综述

随着信用债规模逐步扩大，信用债违约成为关注的焦点，越来越多的学者从各种角度研究信用债违约。传统KMV模型常用于信用债违约预测。潜力和冯雯静（2020）基于2015—2019年的面板数据，采用KMV模型预测了2020—2023年地方政府专项债券的预期违约概率。Ephraim等（2022）对KMV原始模型做了改进，使其不仅可以估计信用违约概率，还能估计以交易成本为代表的市场摩擦和基于模糊性建模的不确定性；他们选择南部非洲银行进行验证，结果表明银行的负债、股权或资本成本以及不确定性与其违约风险呈正相关关系。

在影响因素方面，国内外学者从不同角度对债券违约特征进行研究。Nguyen（2021）研究了1995—2012 年间国际货币基金组织 （IMF）的援助计划对 20 个国家企业违约风险的影响，发现IMF的援助与企业违约风险异常增加有关。在针对我国情况的研究中，Xu等（2020）发现不同省份的信用债违约概率在地域分布上存在明显差异。张春强等（2019）发现公司从业性质与债券违约具有明显的相关关系。还有研究表明财务指标（潘泽清，2018）、企业杠杆率变化（孙立行等，2021）、 企业特征和发行结构（王雪标等，2018）、企业生命周期（高咏玲等，2017）和民企互保（钟金龙等，2021）与信用债违约具有明显相关性。

随着机器学习在金融领域的广泛应用，一些学者已将组合预测与集成预测的方法相结合，构建了以机器学习算法为基础的集成预测模型。Karol（2019）在预测波兰的通货膨胀数据时，发现和单个模型相比，将Bagging算法与单个隐含层的前馈神经网络结合的模型展现出更好的预测性能。Abellán和Mantas（2014）以澳大利亚、德国和日本的信用数据为研究对象，证明Bagging 集成算法具有明显优势。Yin（2020）在股票溢价预测方面采用了Bagging集成算法，并与LASSO方法进行了比较，结果表明无论是经济繁荣时期还是经济衰退时期，Bagging算法均超过LASSO方法获得了更为显著的经济收益。王康等（2021）在预测电力系统短期负荷时，运用Bagging集成算法对原始模型进行集成处理，提高了预测精确度。Jiang等（2020）从多模型集成的角度，通过Stacking集成算法提高预测性能。丁岚和骆品亮（2017）采用Logistic回归、决策树和支持向量机作为基分类器，并以支持向量机作为次级学习器构建了一个Stacking集成框架，用于评估违约风险；通过与单一学习器进行比较， Stacking集成框架展现出了更好的预测性能。由此，本文做出如下创新：

一是在已有研究中，Bagging集成算法一般应用于同质模型的集成，而本文试将Bagging集成算法应用于异质模型的集成，同时通过与Stacking集成算法进行比较，全面评估不同集成策略在信用债违约预测方面的预测效果。二是在相关文献中，虽然集成算法被广泛应用于预测问题，但很少深入分析模型预测的因果关系。本文针对这一问题，引入SHAP可解释算法（Lundberg和Lee， 2017）解释模型预测背后的决策逻辑。与传统的只关注预测结果不同，本文着重分析每个特征对预测结果的贡献，深入挖掘模型的因果关系，从而提高模型的可信度和实用性，也强调了对模型决策过程的解释和理解的重要性。

三、研究设计

本文旨在构建一种集成学习方法，通过集成多种算法实现对信用债违约概率的预测。在对上述多种研究成果进行分析和总结的基础上，选择预测性能较佳的单一算法（支持向量机、逻辑回归、高斯朴素贝叶斯和伯努利朴素贝叶斯），提出基于Bagging集成算法的框架来预测信用债违约情况，并将其与Stacking集成学习方法进行比较，验证Bagging集成算法的预测性能；然后通过SHAP可解释算法，深入分析模型的预测结果，并揭示指标特征值对于结果的影响程度和方向。

（一）Bagging集成算法

Bagging集成算法能够将多个预测模型相结合，每个模型都使用从原始训练集中采样得到的子训练集来构建（Breiman， 1996）。在进行预测时，通过对训练集进行随机化抽样处理，减小了预测结果的方差，避免了过拟合问题，使得预测结果更加稳定（王康等，2021）。Bagging集成算法的步骤如下：

（1） 在原始数据集D中，利用有放回的随机抽样方式多次抽取m个样本，形成n个数据集d1， d2， …， dn。假设每个样本被选中的概率相等。

（2） 使用n个基模型对对应的n个数据集d1， d2， …， dn进行训练学习，在理想情况下，最终得到n个不同的模型e1， e2， …， en。

（3） 将n个不同的模型e1， e2， …， en的预测结果取平均值作为最终的集成预测结果（谭文侃等，2022）。

（二）Stacking集成学习算法

Stacking集成学习算法将多个分类或回归模型进行聚合，使模型的边界更加稳定，降低了过拟合的风险（Guo等，2020）。具体过程如下：假设有n个基础学习器，训练集包含m个样本，每个基础学习器对每个样本都进行预测，这些预测输出组成一个元特征矩阵X：

其中，xij表示第i个样本由第j个基础学习器预测的输出。元学习器使用元特征矩阵X作为输入值，对应的真实标签y 作为输出值进行训练，得到元模型。在测试时，先使用基础学习器进行预测，得到元特征矩阵，然后用元模型对元特征矩阵进行预测，得到最终的集成预测。

（三）SHAP可解释算法

SHAP（Shapley Additive exPlanations）可解释算法是一种用于解释机器学习模型预测结果的方法。它基于博弈论中的SHAP值，为每个特征提供了一个重要性分数，以说明其对于模型预测的贡献。在现有的机器学习模型中，通常很难直接理解模型的预测结果，而SHAP可解释算法有助于理解模型中每个特征对预测结果的影响程度，为模型的可解释性提供了有力支持（Lundberg和Lee，2017）。

SHAP值在机器学习中的应用基于以下公式进行计算：

其中，SHAPi（ f ）是特征i在预测函数f中的SHAP值，n是输入特征的数量，J是输入特征的索引集，x∈X是输入样本。fx（S）表示将输入S与i的组合送入模型中，并预测出输出结果，即S对预测f的共同影响。而fx （S∪i）则表示在保持其他特征不变的情况下，将输入i与S的组合送入模型中所预测的输出结果，即S∪i对预测f的影响。|S|表示集合S的大小， S∈J ＼ i 表示从特征集中选择一个不包含i的子集S。公式中的系数是SHAP值公式的系数，用于计算每个特征的平均边际贡献（林娜等，2023）。

四、数据选择与处理

（一） 数据说明

本文数据来源于WIND数据库，选择从2014年1月1日—2021年12月31日的违约信用债作为违约样本，对于同一主体发行的不同信用债认定为不同样本，共计1 067只信用债。其中，60.12%的信用债主体评级在B级及以下，62.71%的信用债的债项评级在B级及以下。69.61%的违约信用债由民营企业发行，44.75%的违约信用债在银行间债券交易市场进行交易，34.05%的违约信用债在上海交易所进行交易，18.86%的违约信用债在深圳交易所进行交易。违约信用债的种类主要是私募债（255只）、一般公司债（249只）和一般中期票据（246只）。为了确保所选信用债在观察周期（2014年1月1日—2021年12月31日）内不会发生违约，本文在2021年12月31日之前到期的信用债中进行选择，并依据所属行业和资产规模按照1∶2的配对比例为违约信用债选择匹配样本作为对照组。部分信用债主体信息不完整，需要从样本中剔除，最终确定违约信用债769只，对照组987只信用债，用于本研究。

（二）风险预警指标选择及数据预处理

在构建信用债违约风险预警指標体系时，本文选择宏观指标、债项指标和财务指标作为主要考虑因素。宏观指标的选取和处理参考Cakmakli和Van dijk（2016）的研究；债项指标和财务指标除了考虑现金流质量、短期偿债能力、长期偿债能力、营运能力、盈利能力和发展分析6个方面外，还参考了蒋敏等（2021）的指标体系，并将筛选出的所有变量根据指标的属性分为定量指标和类别指标。对于类别指标，按照标签编码方案，将每个类别映射到数值。为了消除不同单位和方差对结果的影响，依据公式（3）对数据进行归一化处理，并进行上下1%的缩尾处理剔除异常值，通过显著性、相关性和多重共线性检验，最终筛选出33个指标，其中定量指标27个、定性指标6个（见表1）。

式中xi表示各个样本，xmax表示样本最大值，xmin表示样本最小值。

五、实验及结果分析

（一） 违约预测模型的构建

本文选择上述33个指标建立新的信用债评级系统，并以此为基础构建信用债违约预测模型；选择支持向量机、逻辑回归、高斯朴素贝叶斯和伯努利朴素贝叶斯作为基分类器，采用Bagging集成算法和Stacking集成算法构建集成模型。同时，将这些集成算法与传统KMV模型进行对比，旨在确定最佳预测模型。

为了降低模型的过拟合程度，并且尽可能地从数据中获取信息，同时让模型的预测性能不会因为数据集的划分而过于敏感，本次实验将样本进行划分，60%作为训练集，40%作为测试集，进行十折交叉验证，重复三次，并将每次重复的结果求平均值以获得最终结果。

在进行违约预测时，KMV模型和机器学习算法得到的预测结果存在差异。KMV模型预测的是违约概率，而机器学习算法常用于预测信用债的类别（即是否会违约）。为了进行统一的评估和比较，参考 Zhao和Chen（2022）的研究，通过大多数样本的平均违约距离来判断企业违约的标准。研究发现大多数企业的违约距离在-5—7之间，平均值为2，因此，若违约距离小于2，该企业发行的信用债将被判定为违约；若违约距离大于或等于2，该企业发行的信用债将被判定为非违约。

由于本文违约样本和非违约样本在数量上存在不平衡，模型的预测分类评价指标选择准确率（accuracy）、精确率（precision）、召回率（recall）和F1，这样不会受到数据分布不均的影响，还能更有效地反映模型预测性能。其中准确率（accuracy）是指分类器正确预测的样本数与总样本数之比。精确率（precision）是指在分类为正类的样本中，分类器正确预测为正类的样本数与所有预测为正类的样本数之比。召回率（recall）是指，在所有真正为正类的样本中，分类器正确预测为正类的样本数与所有真正为正类的样本数之比。F1值是精确率和召回率的调和平均数，它综合考虑了分类器的精确率和召回率。各指标表达式见公式（4）—（7）。

其中TP、FP、FN和TN来自分别以真实值（T）和预测值（F）的positive （P）和negative （N）组成的混淆矩阵 。

（二） 基于不同模型的测算结果分析

表2—表4展示了各个模型的预测性能比较结果，表2是单一模型和传统KMV模型的预测性能比较，表3是分别以不同模型为基分类器的同质Bagging集成算法和异质Bagging集成算法的预测性能比较，表4是分别以不同模型为基分类器的同质Stacking集成算法和异质Stacking集成算法的预测性能比较。和其他算法相比，KMV模型在accuracy、precision、recall和F1上的综合性能弱于其他算法（除了F1略高于高斯朴素贝叶斯），而集成算法相对于单一算法在预测性能上有一定程度的提高，并且异质集成算法优于同质集成算法。这是因为集成算法可以弥补单一模型的缺点，从而获得更稳定、更准确的预测结果，并且异质集成算法使用不同类型或不同参数设置的基础模型，更有可能产生不同的预测错误。这种差异性有助于减少集成模型的偏差，提高整体性能。在异质集成算法中，Bagging集成优于Stacking集成，原因是在Bagging集成中，每个基分类器都通过自主随机采样训练，加强了模型的泛化能力，并在它们之间引入了一些随机性，减少了过拟合产生的可能，在处理一定的噪声和不平衡的数据时，可通过随机抽样和多模型平均减少噪声的影响，并且在处理不平衡数据时能够更好地平衡各类别的预测结果。Stacking集成算法则需要对多个基分类器的输出进行组合，很容易受到性能不好的模型影响，且数据的噪声和不平衡性还会影响其模型组合和元分类器的选择；此外，额外引入的元分类器可能会增加整体模型的复杂度，很可能导致出现过拟合问题。

（三）信用债违约指标重要性分析

和其他模型相比，Bagging异质集成算法有着更优的表现，具备良好的预测能力。但其结构过于复杂，在可解释方面不如一些简单模型易于理解，所以引入SHAP可解释算法建立辅助理解模型。

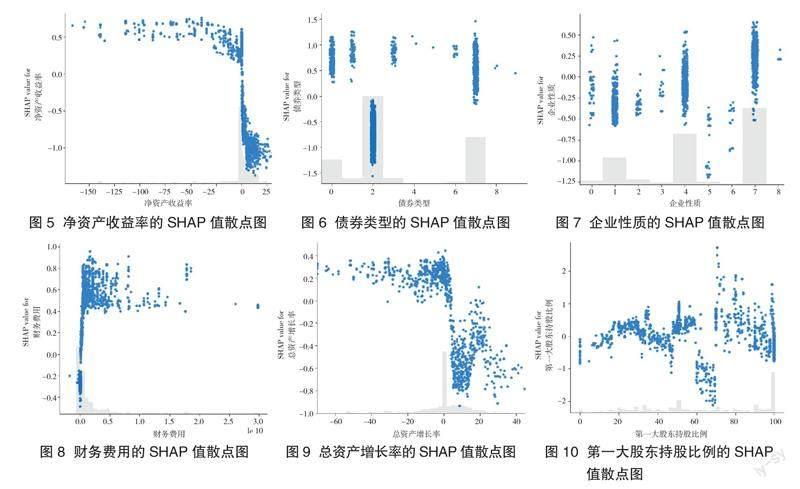
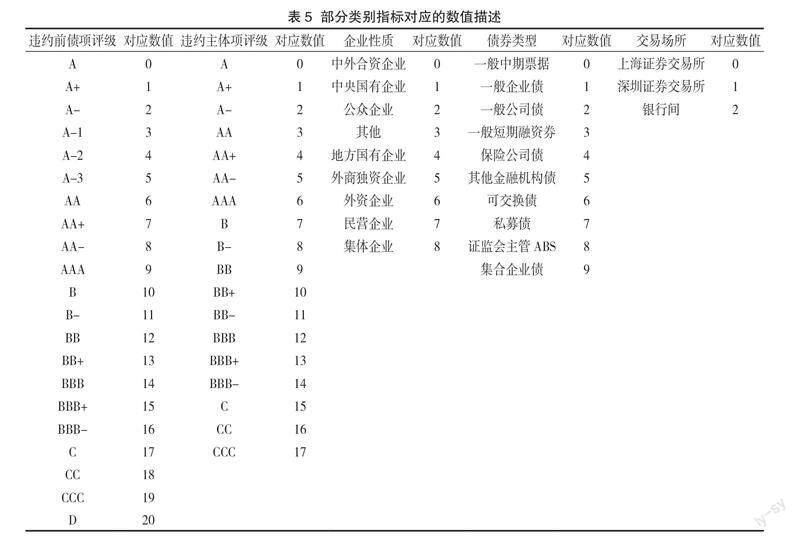
图1 展示了SHAP特征值的变化如何影响信用债违约概率。采用不同颜色表示指标特征在样本点上的取值大小，红色样本点表示指标在该样本上取值较大，蓝色样本点表示指标在该样本上取值较小。每个指标特征的图形由集合中所有样本点构成。以 SHAP 值=0为分界线，当样本點位于左侧时，该指标特征对应样本的 SHAP 值为负，表示指标特征取该样本点的值时对输出违约概率有负向贡献，即降低违约概率；当样本点位于右侧时，指标特征取对应值时对输出违约概率有正向贡献，即增加违约概率。因此，对输出违约概率有正向贡献的线性关联指标，图像应呈现出左边蓝色、中间紫色和右边红色；而对输出违约概率有负向贡献的线性关联指标，图像应呈现出左边红色、中间紫色和右边蓝色。结果表明，违约前债项评级、违约前主体评级、交易所、净资产收益率、债券类型、企业性质、财务费用、总资产增长率以及第一大股东持股比例对信用债违约概率预测发挥着重要的作用（见图1）。这些指标的SHAP值散点图见图2—图10，图中部分类别变量以数字代表，具体见表5。

结合表5和图2—图10可知，在银行间交易和深圳交易所交易的信用债违约概率较大（见图4）；违约前主体评级和违约前债项评级都是评级越低，违约概率越大（见图2和图3）；债券类型中，一般中期票据、一般企业债、一般短期融资券和私募债的信用债违约概率较大（见图6）；企业类型中，民营企业、国有企业和中外合资企业的信用债有较大违约概率（见图7）。

根据图5可知，整体来看净资产收益率和信用债违约概率呈负相关关系。这是因为净资产收益率为负不仅意味着企业由于运营不善，在经营过程中有高额费用产生或者其他负面经济因素，面临亏损，从而导致现金流紧张，难以满足债务偿还要求，增加违约风险；还可能导致企业的信用评级下降，增加企业融资成本，进一步恶化企业的财务状况，限制其债务偿还能力，从而导致违约风险上升。而净资产收益率大于等于0则意味着企业在运营方面取得了盈利，这增强了企业的财务稳定性，使其更有能力偿还债务，能更好地应对经济波动，从而降低违约风险，降低信用债违约概率。

根据图8可知，随着财务费用的上升，信用债违约概率呈现先上升后缓慢下降的趋势。这是因为初期的财务压力可能使企业的现金流受到挤压，难以按时支付债务，导致违约概率急剧上升。在财务费用增高后，企业可能会采取一些措施来应对财务压力，例如寻求新的融资、削减成本、提高盈利能力等，这些措施可能会在一段时间内缓解财务压力，降低信用债违约概率的增长速度。随着时间的推移，企业也会进行财务调整和优化來改善其财务状况，包括重新规划债务结构、改善经营绩效、降低财务风险等，这些措施能够逐渐降低违约概率。

根据图9可知，当总资产增长率小于0时，信用债违约风险高企，而当总资产增长率大于0时，信用债违约概率先增加后减少直到趋于平缓。这是因为在总资产增长率的不同阶段，企业面临的财务压力、债务负担和市场环境等因素交织影响着违约概率的变化。当总资产增长率大于0且数值较低时，企业可能在相对稳定的状态下运营，财务状况较好，违约概率较低；然而，随着企业总资产增长率的提高，企业可能开始扩张、投资和拓展市场，在这个阶段，企业需要投入更多的资金来支持新项目，可能导致财务压力增加，从而提高了违约概率；企业在高速增长的过程中可能会不断优化其财务结构，改善债务管理、资金配置等，在长期会降低债务风险，提高企业的财务稳定性，进而将违约概率控制在一个较低的平稳数值。

由图10可知，第一大股东持股比例与信用债违约概率之间的关系呈现出复杂的动态，这可能是因为第一大股东持股比例处于不同区间时，受到不同的影响机制的主导，呈现出不同的变动趋势。整体来看，当第一大股东持股比例较低时，其对企业决策的影响可能有限，此时，即使持股比例稍有增加，对企业运营和财务风险的影响可能也不太显著，因此违约概率的增长较为缓慢。随着第一大股东持股比例的增加，他们获得了更大的企业控制权和决策权，在一定范围内，这有助于提高企业运营效率，管理财务风险，控制违约概率；但当第一大股东持股比例超过某一阈值后，可能导致逆向效应，即过高的持股比例使第一大股东控制权过于集中，导致决策偏向性明显，影响企业的正常经营，这可能导致风险集中或不稳定，使违约概率再次增加。当第一大股东持股比例达到一定水平后，持续增加持股比例可能不再显著改变企业的控制和决策权，而更多地意味着企业经营和财务状况的稳定性，市场信心得以提升，从而减少了违约的风险。此外，企业的治理结构、市场环境、经营战略等因素都可能影响这种复杂的关系，使之呈现出一种多变、不稳定的模式。

六、结论与不足

随着近年来信用债市场的迅速发展，信用债违约风险逐渐引起关注。本文旨在寻找提高预测信用债违约水平的模型，并探讨信用债违约的影响因素，以期为投资者提供更准确的风险评估和决策参考。本文选择2014—2021年全部的违约信用债作为违约组，并依据所属行业和资产规模按照1∶2的配对比例为违约信用债选择匹配样本，最终得到信息完整的违约信用债769只，对照组非违约信用债987只。本文通过参考相关文献，确定了定量指标，并结合信用债市场变化选择部分类别指标建立信用债违约预警指标体系。在研究方法上，本文旨在探索基于不同基分类器的集成算法在信用债违约预警上的应用，并比较不同算法性能的优越性；考虑到集成算法存在的黑箱问题，最后选择性能最佳的模型进行特征重要性分析。与传统模型相比较，机器学习算法表现出更好的预测性能。与同质集成算法相比，异质集成算法在提高预测精度方面相对较强。此外，针对异质集成算法，Bagging集成算法的预测效果优于Stacking集成算法。总而言之，在提高预测准确性方面，异质集成算法具备较大潜力，并且Bagging集成算法在该领域的应用效果更加显著。

此外，基于SHAP的特征分析，本文得出了对建立预警指标体系具有重要意义的指标。研究结果显示，违约前债项评级、违约前主体评级、交易所、净资产收益率、债券类型、企业性质、财务费用、总资产增长率以及第一大股东持股比例在信用债违约预测中有很大影响，值得投资者和监管部门关注。这些指标大部分是类别指标，因此在今后构建信用债违约预警体系时，可以考虑非量化指标和量化指标协同发挥作用，共同构建信用债违约预警指标体系，以全面衡量信用风险（雷欣南等，2022）。

本文的研究也存在一些局限性。例如数据集规模较小、缺乏横向数据，影响了结果的适用性与普遍性。此外，特征之间的交互关系也需要更精细的探究。在未来研究中可以增加数据集规模，加入更多的影响因素，同时使用更多的算法对模型进行优化，以提高模型预测精度并寻找最合适的模型，最终投入实践，为信用债违约风险控制策略的制定提供科学可行的参考。

参考文献：

[1] 杜渐，周冠男. 2021年信用债市场违约年鉴（下）——案例篇[EB/OL].（2022-01-26）[2023-10-30]. https：//cj.hczq.com/paidArticles/54915？t=1687338598270. 2022.01.26.

[2]潜力，冯雯静.地方政府专项债券违约风险 ——基于KMV模型的分析[J].统计与信息论坛，2020，35（07）：35-44.

[3] EPHRAIM M， ERIYOTI C， FARAI K. Fuzzy structural risk of default for banks in Southern Africa [J]. Cogent Economics and Finance， 2022， 10（01）： 2141884.

[4] NGUYEN T T. The effect of International Monetary Fund programs on corporate default risk[J]. International Journal of Finance & Economics，2021，28（01）：1156-1174.

[5] XU Z H， FAN W， ZHU F. Research on regional debt risk in Hubei province based on modified KMV model [J]. IOP Conference Series： Materials Science and Engineering， 2020， 768（05）： 052129.

[6]張春强，鲍群，盛明泉.公司债券违约的信用风险传染效应研究——来自同行业公司发债定价的经验证据[J].经济管理，2019，41（01）：174-190.

[7]潘泽清.企业债务违约风险Logistic回归预警模型[J].上海经济研究，2018，30（08）：73-83.

[8]孙立行，吴雄剑，唐逸舟.货币政策、杠杆水平与债券违约[J].苏州大学学报（哲学社会科学版），2021，42（06）：115-126.

[9]王雪标，王晰，孙晓林.我国中期票据发行信用利差的影响因素研究[J].山西财经大学学报，2018，40（09）：18-32.

[10]高咏玲，杜晗，佟岩.生命周期视角下并购类型对上市公司信用风险的影响——基于KMV模型的实证研究[J].科学决策，2017（03）：35-48.

[11]中泰证券课题组，钟金龙，冯玉梅.公司信用债违约风险预警与防范研究[J].证券市场导报，2021（02）：2-10+18.

[12]KAROL G S. Bagged neural networks for forecasting Polish （low） inflation[J]. International Journal of Forecasting，2019，35（03）：1042-1059.

[13] ABELL?N J，MANTAS C J. Improving experimental studies about ensembles of classifiers for bankruptcy prediction and credit scoring[J]. Expert Systems with Applications，2014，41（08）：3825-3830.

[14] YIN A W. Equity premium prediction and optimal portfolio decision with Bagging[J]. The North American Journal of Economics and Finance，2020，54：101274.

[15]王康， 张智晟， 撖奥洋， 等.基于Bagging的双向GRU集成神经网络短期负荷预测[J]. 电力系统及其自动化学报， 2021， 33（10）： 24-30.

[16] JIANG M Q，LIU J P，ZHANG L，et al. An improved Stacking framework for stock index prediction by leveraging tree-based ensemble models and deep learning algorithms[J]. Physica A：Statistical Mechanics and Its Applications，2020，541：122272.

[17]丁岚，骆品亮. 基于Stacking集成策略的P2P网贷违约风险预警研究[J]. 投资研究，2017，36（04）：41-54.

[18] LUNDBERG S M， LEE S-I.  A unified approach to interpreting model predictions [C].  Proceedings of the 31st International Conference on Neural Information Processing Systems， 2017： 4768-4777.

[19] BREIMAN L. Bagging predictors[J]. Machine Learning，1996，24（02）：123-140.

[20]谭文侃，胡南燕，叶义成，等.基于四大集成学习的岩爆烈度分级预测[J].岩石力学与工程学报，2022，

41（S2）：3250-3259.

[21]GUO X F，GAO Y，ZHENG D，et al. Study on short-term photovoltaic power prediction model based on the Stacking ensemble learning[J]. Energy Reports，2020，6：1424-1431.

[22]林娜，冯珊珊，王斌，等.基于XGBoost模型的高分辨率遥感滑坡快速提取与分析研究[J/OL].武汉大学学报（信息科学版）：1-12[2023-10-30].https：//doi. org/10. 13203/j. whugis20220296.

[23] ?AKMAKL C，VAN DIJK D. Getting the most out of

macroeconomic information for predicting excess stock

returns[J]. International Journal of Forecasting，2016，

32（03）：650-668.

[24] 蒋敏，周炜，史济川，等.基于fsQCA的上市企业债券违约影响因素研究[J].管理学报，2021，18（07）：1076-1085.

[25] 朱武祥，廖静秋，詹子良，等.回归金融原理：企业财务危机预警研究述评与展望[J].清华大学学报（自然科学版），2023，63（09）：1467-1482.

[26] ZHAO Y， CHEN Y.  Assessing and predicting green credit risk in the paper industry [J].  International Journal of Environmental Research and Public Health，2022，19（22）：15373.

[27]雷欣南，林乐凡，肖斌卿，等.小微企业违约特征再探索：基于SHAP解释方法的机器学习模型[J/OL].中国管理科学：1-13[2023-10-30].https：//doi.org/10.16381/j.cnki.issn1003-207x.2021.0027.

（责任编辑：唐诗柔）

Study on Credit Bond Default Prediction Model Based on Integrated Algorithms and Its Influencing Factors

ZHENG Yixin， WANG Chongren

（ Shandong University of Finance and Economics ）

Abstract： Taking credit bonds from 2014 to 2021 as the research object， this paper constructs Bagging and Stacking integrated learning models using single algorithms （logistic regression， Gaussian naive Bayes， support vector machine and Bernoulli naive Bayes） respectively， and compares them with the results of single algorithms and traditional methods （KMV model） to explore how to improve the accuracy of credit bond default prediction， prove the reliability of the Bagging integrated algorithm， and study the important indicators in credit bond default through the SHAP interpretable algorithm. The results show that： the 4 single machine learning models are superior to the traditional KMV model in prediction accuracy; further integration of machine learning models finds that homogeneous integrated algorithms are not as good as heterogeneous integrated algorithms in improving predictive performance， and the prediction accuracy of heterogeneous Bagging integrated algorithm is better than that of Stacking. Combining the best-performing heterogeneous Bagging integrated algorithm with the SHAP interpretable algorithm， 9 indicators that are valuable for identifying credit bond defaults are obtained， which are rating before default， issuer rating before default， exchange， return on net assets， bond type， enterprise nature， financial expenses， growth rate of total assets， and the proportion of the largest shareholder. Identifying key indicators is instructive for credit bond default prediction.

Keywords： Credit bond default; Risk warning; Bagging ensemble algorithm; Stacking ensemble algorithm; SHAP interpretable algorithm

收稿日期：2023-06-27

作者簡介：郑怡昕，硕士研究生，山东财经大学，研究方向为信用债、机器学习。

王重仁，博士，副教授，山东财经大学，研究方向为机器学习。

基金项目：山东省软科学项目“山东省互联网生态体系构建与发展对策研究”（2021RKY02023）。