上海地铁运行引起软土场地振动实测与预测模型研究
吴德顺 顾晓强,2,* 刘鑫
(1.同济大学土木工程学院地下建筑与工程系,上海 200092;2.同济大学岩土与地下工程教育部重点实验室,上海 200092)
0 引 言
近年来,为缓解城市交通压力,大量地铁建成并投入运营。截止到2022年12月31日,内地53个城市累计建成运营地铁9 584 km。然而,地铁在城市环境中常邻近或下穿既有建筑物,其引发的环境振动问题受到了广泛关注。因此开展邻近地铁场地环境振动评估和预测已成为环境振动研究的热点和难点问题之一。轨道交通环境振动主要由轨道不平顺、车轮和轨道的不连续等因素引起[1]。产生的振动波以体波为主,并叠加面波通过土体传播到邻近建筑物地基,最后引发建筑物和结构的振动和噪声污染,对精密仪器的正常使用、古建筑保护和人体舒适性产生不利影响[2-3]。一般邻近地铁的拟建项目初期需要对地铁运行引起的振动水平进行预测和评估,其中首先需要针对场地开展振动实测,随后结合实测开展场地的振动预测。目前结合实测的振动预测主要包括利用实测数据校准后的有限元模型进行预测和根据实测建立可靠的振动预测模型来进行预测。
在利用实测数据校准后的有限元模型进行预测研究方面,Ma等[4]利用实测数据校准后的地铁列车-轨道-隧道-土体三维有限元模型预测了两条空间重叠的地铁线路引起的振动。岳建勇[5]结合实测隧道壁振动和有限元计算开展了地铁交通激发周边建筑物振动响应预测分析。郭瑜[6]基于弹塑性分析模型研究了地铁车辆段上盖隔震单塔结构的模态特征和减震效果。
根据实测建立环境振动预测模型的研究主要以理论研究成果为基础,结合现场实测数据建立经验或半经验的预测模型。预测模型所需计算参数较少、计算方便,在地铁周边项目建设初期可快速预测地铁振动影响范围和大小,因此在国内外得到了广泛的使用。预测模型可主要分为振级预测和峰值预测两个类别。我国规范[7]推荐采用链式衰减公式进行地表振级预测,即以地铁轨道处振级为基础,同时考虑传播路径上的衰减和建筑物内衰减修正。也有学者[8-9]提出考虑列车车速和传播距离衰减的振级修正。此外峰值的预测包括速度、位移和加速度峰值的预测。地铁地表运行线或高铁引起的地表振动时程峰值预测主要基于Bornitz公式或其改进公式,如Ren等[10]基于Bornitz公式提出的层状均质介质振动衰减模型研究了高铁运行引起的地面振动响应,并给出了上海土的材料阻尼系数和几何阻尼系数的典型取值。然而利用Bornitz公式预测埋置地铁引起的地表振动峰值鲜有报道,因此其适用性需进一步探讨。
本文首先开展了上海地铁11号线振动实测,分析了地铁运行引起场地振动的典型加速度时程、频谱和1/3倍频程谱,并利用Bornitz公式分析了加速度峰值随距离的衰减规律。其次基于对数衰减模型拟合了实测地面振级,研究了模型中拟合参数A与振动频率的相关性;并基于Bornitz振动传播公式提出了地面振级拟合模型,探讨了材料阻尼系数、频率无关材料阻尼系数以及阻尼比的取值。最后对比了对数衰减模型和Bornitz模型预测地铁运行引起地表振级的效果。
1 工程概况
某拟建大型商住综合体位于上海浦东新区,该项目北侧临近包括地铁11号线和6号线在内的四条地铁线路,南侧、西侧和东侧均为交通繁忙的主干道。地铁运行和路面交通振源引起的振动情况复杂。其中地铁11号线下行线隧道边缘与拟建地面裙楼地下室最近距离约10 m,隧道埋深为13.5 m,内径和外径分别为5.5 m和6.2 m,衬砌厚度为0.35 m。地铁隧道与拟建建筑物位置关系如图1所示。
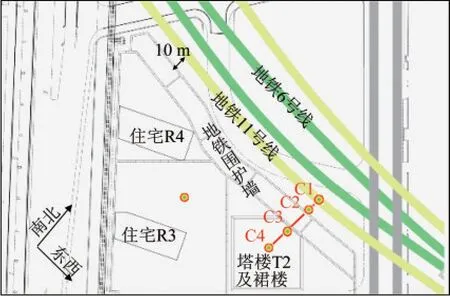
图1 地铁与拟建建筑物位置关系图Fig.1 The positions of the tunnel and the building
由于该大型商住综合体与地铁距离近,建成后地铁列车运行引起建筑物振动可能超过相关规范要求,对室内振动舒适性造成不利影响。因此需要在建筑施工前开展场地振动实测,明确地铁运行引起的场地振动水平。为了有效评估地铁运行对该拟建大型商住综合体振动舒适性的影响,选择地铁最近的塔楼T2及裙楼为评估对象。沿地铁11号线隧道垂直方向在地表共布置4个测点,如图1所示。其中测点C1位于地铁11号线靠近场地一侧隧道中心正上方地表,测点C2、C3、C4与C1的距离分别为6 m、22 m和70 m。
本次测试振动控制标准采用上海市2010年起实施的《城市轨道交通(地下段)列车运行引起的住宅室内振动与结构噪声限值及测量方法》[11]。该标准以铅垂向最大Z振级作为评价量,振动限值见表1。表中的各类分区根据《上海市环境噪声标准适用区划》[12]确定。根据地理位置本场地为2类区,竖向振动限值昼间(06∶00—22∶00)和夜间(22∶00—06∶00)分别为72 dB和69 dB。
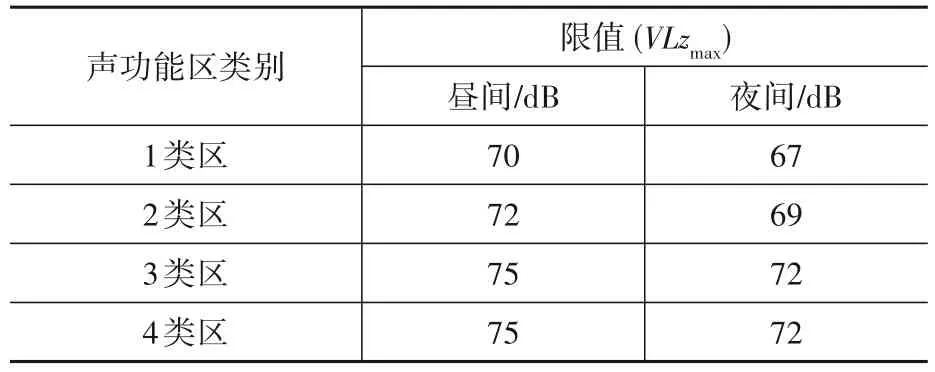
表1 城市轨道交通列车运行引起的住宅室内振动限值Table 1 Vibration limits in dwellings caused by moving vehicles of urban rail transit [11]
2 现场振动实测和结果分析
本次测试采用微振动测试仪TROMINO,如图2所示。仪器长、宽、高分别为15 cm、10 cm和10 cm。该仪器是一种可用于测试场地微振动的超轻量化、超紧凑型仪器,集采集系统、加速度感应系统和数据存储系统于一体,可长时间无间断采集,并可同时采集三维空间内三个相互垂直方向的速度和加速度时程。具有测试高度智能化、测试方便、精度高等优点,满足本次测试的要求。仪器频域测试范围为0.1~1 024 Hz,高增益渠道速度精度为±0.01 mm/s,加速度精度为±0.8 mm/s2。

图2 测试仪器以及现场测试图Fig.2 Test instrument and the field test site
为充分考虑地铁运行振动对拟建项目的影响,选择昼间的高峰时间段(16∶30—19∶20)进行测试,该时间段地铁运营周期短且大客流量引起更大的列车轴重,由此引发环境振动的水平较大,对拟建建筑影响是最为严重的。每个测点测试总时长为30 min,保证测试期间上下行列车各不少于5次,测试的采集频率为512 Hz,同时记录各测点的水平和竖向振动时程。
为了评估场地中地铁运行引起的环境振动传播特性,图3对比了地铁11号线经过时地表4个测点的典型竖向时程和频谱。所选取的4个测点与地铁隧道中心的水平距离分别为0 m、6 m、22 m和70 m,与地铁轨道中心垂直向距离均为18.1 m。由图3可知,竖向加速度峰值随着距离的增加逐渐减小,各测点加速度峰值分别为223.38 mm/s2、163.5 mm/s2、39.8 mm/s2和14.4 mm/s2。
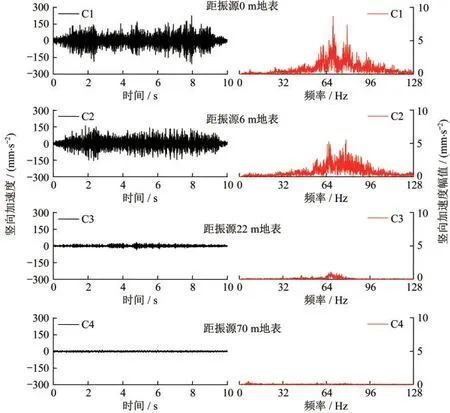
图3 典型加速度时程和频谱图Fig.3 Typical acceleration time histories and frequency spectrum at the ground surface
由图3的典型加速度傅立叶谱可见,在离振源较近的测点C1和C2的频谱曲线中存在清晰的双峰。其中测点C1两个优势频带分别为66~72 Hz和76~82 Hz,每个优势频带内对应幅值最大的频率分别为70 Hz和79.3 Hz。测点C2两个优势频带分别为63~69 Hz和73~80 Hz,每个优势频带内对应幅值最大的频率分别为65.8 Hz和78.4 Hz。对比测点C1和C2频谱结果可知,当与振源水平距离由0 m增大至6 m时,两个优势频带、最大幅值对应频率以及对应频谱幅值均减小。随着与轨道中心线距离的继续增加,在C3测点处仅有一个优势频带,且范围为64~76 Hz,对应最优频率为67.2 Hz。在C4处主要频率范围为0~15 Hz,最优频率为6.6 Hz,此时高频振动已基本衰减。对比各测点频谱曲线可知,地铁列车引起的地面竖向振动优势频率和对应幅值均随着距离增加呈衰减趋势。在近轨道处高频振动占主导,在远离轨道处低频振动占主导。
为进一步对比不同频率振动的衰减特性,图4给出了典型加速度1/3倍频程谱。1/3倍频程是指相邻两个中心频率之比和每个1/3倍频程范围的上下限频率之比均为21/3。1/3倍频程中心频率和振级的计算方法如下:
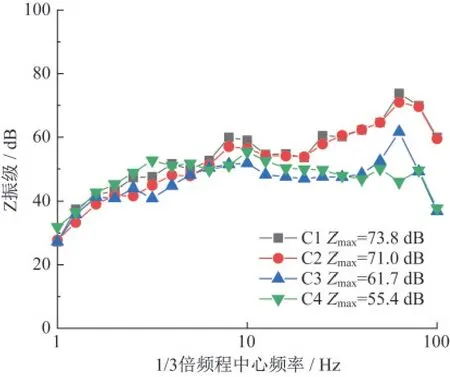
图4 典型1/3倍频程图Fig.4 Typical 1/3 octave of accelerations at the ground surface
式中:fc、fu和fl分别为中心频率和上下限频率;arms为加速度有效值;ai为实测加速度值;N为实测加速度时程总采样点个数;a0=10-6m/s-2,为基准加速度;VAL为振动加速度级。
计算时首先根据式(3)计算该频带范围内的加速度有效值,然后根据式(4)计算振动加速度级,最后按照《城市轨道交通(地下段)列车运行引起的住宅室内振动与结构噪声限值及测量方法》[11]规定的1/3倍频程中心频率的Z计权因子进行修正得到Z振级。
由图4可知,裙楼地表处的C2测点铅锤向最大Z振级为71 dB,塔楼T2处的铅锤向最大Z振级为61.7 dB,均满足规范的昼间72 dB振动限制要求。由图4还可知,随着与轨道中心的水平距离由0 m增大至70 m,当中心频率小于2 Hz时,Z振级衰减不明显,甚至在一些频带内出现了Z振级随距离增加的现象。当中心频率在2~20 Hz范围内时,Z振级随距离增加呈现波动式衰减。当中心频率高于20 Hz时,Z振级随距离增加衰减明显。在80 Hz时振动衰减量达到28.4 dB。综上可知,地铁引起的地面振动低频衰减不明显,中频范围内呈现波动式衰减,高频范围内振动的衰减速度显著快于低频振动。
为了进一步分析地铁运行引起的地表振动随距离的衰减特性,图5对比了5次列车经过时各测点在三个方向上的峰值加速度。由图5可知,在22 m范围内两个水平方向上的加速度峰值显著大于竖向加速度峰值,尤其是东西向加速度。这主要与地铁在曲线段上运行所产生的向心力有关。He等[13]也在其研究中发现了类似现象。目前规范主要考虑竖向振动的影响,然而由本文结果可知对于曲线段地表水平加速度峰值可达竖向的3~4倍。因此对于曲线段需要特别关注水平向振动的影响。在距振源最远的70 m处,三个方向加速度峰值大致相当。三个方向加速度峰值均随着距离的增加逐渐衰减,未发现振动放大区。其中东西方向的加速度峰值衰减速度最快,而竖直方向加速度峰值的衰减速度最慢。
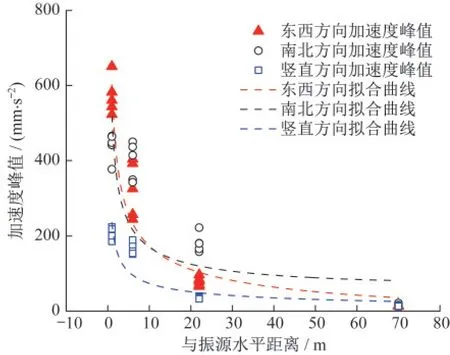
图5 加速度峰值随距离的衰减曲线Fig.5 Attenuation of PGA with distance
地面加速度峰值随距离的衰减规律,一般可采用Bornitz振动传播公式[14]进行定量描述:
式中:a(R)为与振源水平距离R处的加速度振幅;a0为参考点加速度振幅;R0为参考点与振源的水平距离,取为1 m;n为几何阻尼系数;αM为材料阻尼系数。
Bornitz公式中几何阻尼系数n与振源类型、振源位置和振动波的类型有关,Kim等[15]开展了多种情况下几何阻尼系数的取值研究,具体取值详见表2。由表2可知,地铁隧道可近似看作是地下无限长结构,地铁运行引起的振动可看作地下线振源引起的体波。本文进一步对实测各方向的加速度峰值按Bornitz振动衰减公式进行了拟合,拟合得到东西方向加速度峰值衰减公式为AEW=607.99R-0.5e-0.010R,南北方向加速度峰值衰减公式为ASN=517.27R-0.5e-0.0039R,竖直方向加速度峰值衰减公式为AUD=235.78R-0.5e-0.0014R,具体如图5所示。
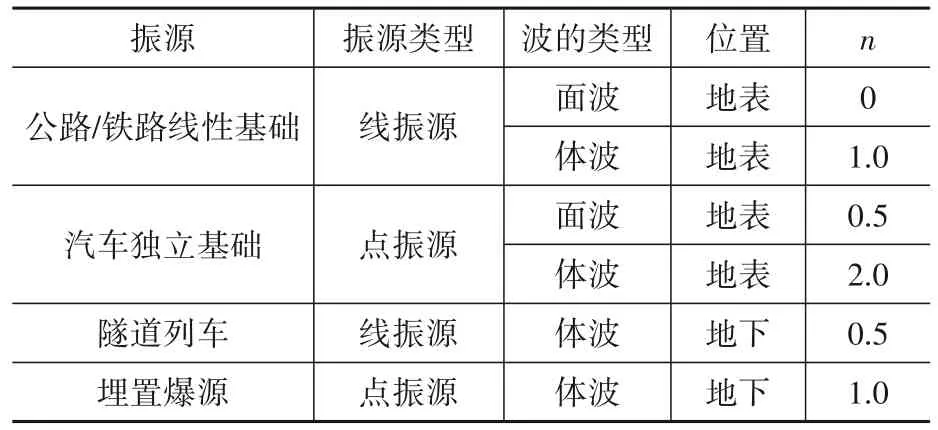
表2 不同振源位置及类型的几何阻尼系数[15]Table 2 Geometric damping coefficients under different vibration sources
3 振动预测模型分析
3.1 基于对数衰减的地面振级预测模型
地铁振动传播过程可认为是由地铁列车与轨道相互作用产生振动,振动经过扣件和道床传递至隧道衬砌,并以点振源或线振源体波的形式在土层中传递至受振点,最后对地下和地表结构产生振动影响。其中因距离扩散和介质吸收引起的振级衰减值一般采用对数公式进行计算。如《环境影响评价技术导则-城市轨道交通的预测方法》(HJ 453—2008)[7]提出的城市轨道交通运行时振级随距离衰减采用公式(6)计算:
式中:VLz为建筑物室外Z振级预测值;VL0为道床振动源强;CD为距离扩散和介质吸收引起的衰减值;参数A与B可以通过类比测试或回归计算得到;由于道床振动源强VL0和B均为待定常数项,因此合并为一个参数进行回归拟合;r为传播距离,可采用公式(7)计算,其中L和H分别为预测点与轨道中心点的竖向和水平向距离。
本研究根据4次地铁列车经过时地面4个测点的实测记录,利用公式(6)进行回归拟合得到待定参数,如图6所示。该工作一方面可以根据实测点振动情况预测其他地面点处的振动,为工程振动舒适性评估提供参考;另一方面可以作为软土地区典型土层振动衰减预测公式为上海类似地质条件的其他工程提供参考依据。
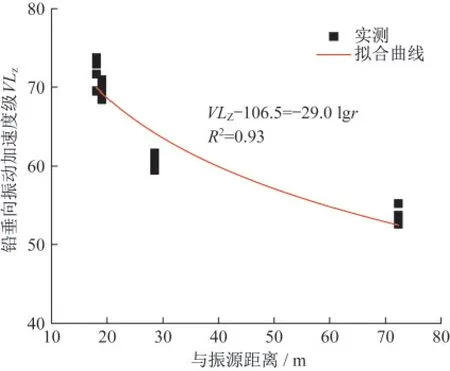
图6 地面Z振级对数回归拟合曲线Fig.6 Logarithmic regression curve of ground Z vibration level
图6给出了地面Z振级与距离之间的对数回归拟合曲线。拟合得到的Z振级随距离的衰减公式为
拟合的回归相关性系数为0.93,表明因距离扩散和介质吸收引起的振级衰减与传播距离具有较强的相关性。基于该公式可对地面其他点进行振动预测。
在此基础上,本文进一步根据式(9)研究了不同频率下的振级衰减规律:
式中:VLZ(f)为与1/3倍频程中心频率f对应的Z振级;VLZ0(f)为与轨道中心距离1 m处的1/3倍频程中心频率f对应的振动级。
为了得到VAL0和A的值,本文采用最小二乘法对每个1/3倍频程中心频率对应的系数A进行了拟合。
图7给出了各1/3倍频程中心频率以及对应的系数A之间的相关关系曲线。由图7可知,系数A随着频率的增加逐渐增大,表明在土体阻尼作用下随着距离的增加,振级的衰减速度随着频率的增加而增大。经过回归分析可以得到系数A与1/3倍频程中心频率之间的相关关系:
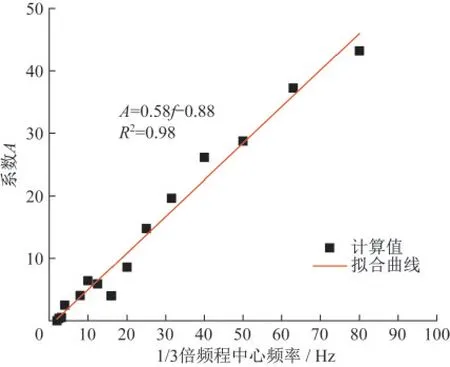
图7 频率和系数A之间关系曲线Fig.7 Relationship between frequency and coefficient A
拟合的回归相关性系数为0.98,表明系数A与1/3倍频程中心频率具有较强的线性相关性。
3.2 基于Bornitz公式的地面振级预测模型
根据式(4)振级的定义,可以将Bornitz公式表示为如下加速度振级形式:
图8给出了地面Z振级与距离之间的Bornitz公式拟合曲线。拟合得到的地面Z振级随距离的衰减公式为
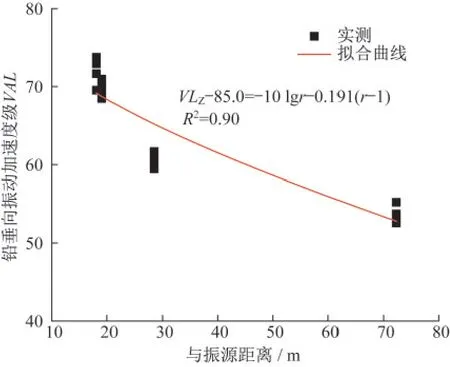
图8 地面Z振级Bornitz公式拟合曲线Fig.8 The regression curve of ground Z vibration level based on Bornitz formula
拟合的回归相关性系数为0.90,表明Bornitz模型也可较好地预测地铁运行引起的地面振级。
为了进一步研究Bornitz公式中材料阻尼系数与频率的关系,采用式(13)对4趟地铁列车经过时地面各测点某个1/3倍频程中心频率对应振级进行了拟合:
由图9可知,材料阻尼系数αM随着频率的增加逐渐增加。1/3倍频程中心频率和材料阻尼系数αM之间具有良好的线性关系,关系曲线为式(14):
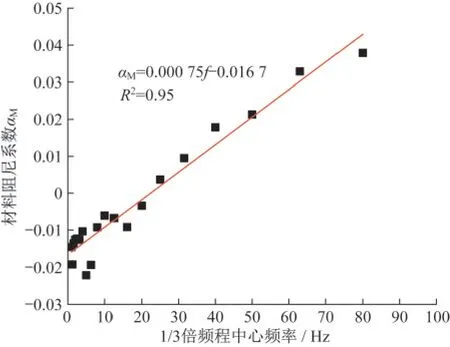
图9 频率和材料阻尼系数之间关系曲线Fig.9 Relationship between frequency and material damping coefficient αM
此外,天然场地的阻尼一般难以量测,因此是振动评估的难点和重点问题之一。本文进一步基于Bornitz公式研究了土体的阻尼特性。材料阻尼系数αM与振动波的频率和土体特性有关,可以用式(15)来表示:
式中:f为振动频率;α0为频率无关材料阻尼系数,主要与土体阻尼比D和波速V有关。
根据不同频率下材料阻尼系数αM和式(15)可以计算得到频率无关材料阻尼系数α0和对应的土体阻尼比D。由于当频率小于20 Hz时振级并不是随着距离的增加而衰减,而是在C4测点处(距离约为70 m)出现了放大的现象,此时拟合得到的材料阻尼系数αM为负值。而土体阻尼必须为正,所以仅对20 Hz以上结果分析频率无关材料阻尼系数α0,结果见表3。由该表可知,除25 Hz和31.5 Hz外,频率无关材料阻尼系数α0随频率变化较小,表明其受振动波特性的影响较小,主要反映的是土体的动力特性。已有诸多学者开展了相应研究并针对不同土给出了α0的统计值。Yang[16]研究指出软土α0范围为(1.3~1.5)×10-3s/m。余宽原等[17]通过对上海磁悬浮列车运行地面振动结果分析得出上海软土场地α0范围为(1.80~2.05)×10-3s/m。Ren等[10]基于地表高铁振动实测数据发现上海软土压缩波对应的α0范围为(0.18~5.72)×10-4s/m,剪切波对应的α0范围为(0.07~2.15)×10-3s/m。本文研究结果与Ren等[10]剪切波对应的α0结果一致。此外,本文根据α0进一步统计了土体阻尼比范围为0.28%~1.0%,其中土体剪切波速取地铁埋深以上土层按厚度等效的剪切波速。
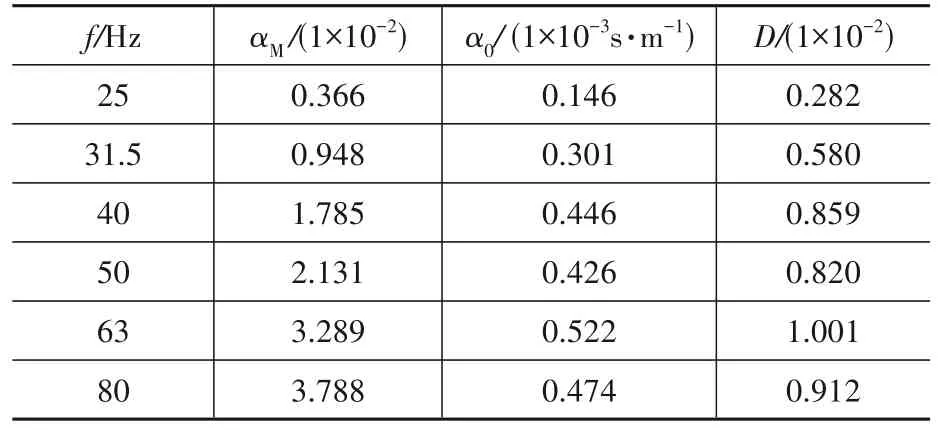
表3 不同振源位置及类型的几何阻尼系数Table 3 Summary of dynamic soil properties for study site
3.3 振级的对数衰减模型和Bornitz模型预测对比
为了对比对数衰减模型和Bornitz模型对地铁运行引起的地表Z振级的预测效果,选取该场地单次列车经过时地表各测点Z振级实测值(该次地铁运行数据未用于前述振级预测公式拟合)。分别由式(8)和式(12)计算得到对数衰减模型和Bornitz模型的Z振级预测值。表4给出了地表Z振级实测值、两种模型预测值和相对误差。由表4可知,由实测数据拟合得到的两种振级预测模型均可较好地预测地表振级,相对误差均小于8%。除C4测点外,其余测点处Bornitz模型预测效果均略好于对数衰减模型。
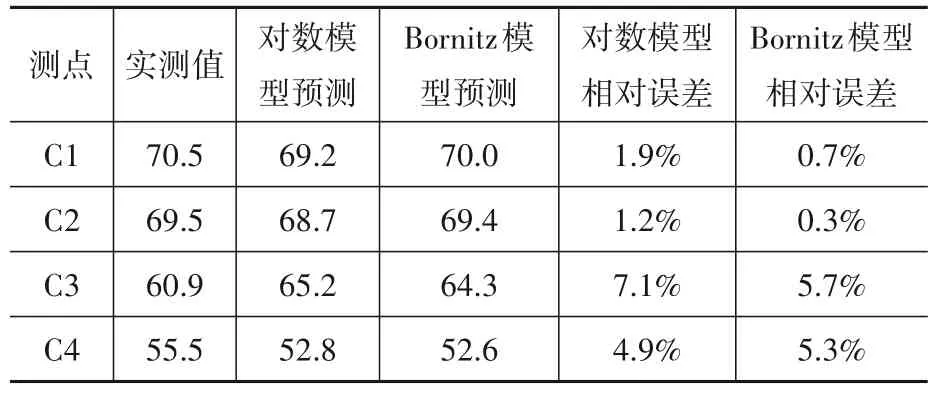
表4 对数衰减模型和Bornitz模型预测的Z振级对比Table 4 Comparison of the predicted vibration level between logarithm model and Bornitz model
为了进一步对比对数衰减模型和Bornitz模型对地铁运行引起的地表测点1/3倍频程的预测效果,选取上述Z振级预测效果对比时的单次地铁运行地表各测点1/3倍频程谱作为预测对象。其中对数衰减模型1/3倍频程谱采用公式(9)进行计算,公式中参数A由公式(10)计算得到。Bornitz模型1/3倍频程谱采用公式(13)进行计算,公式中参数αM由公式(14)计算得到。
图10给出了对数模型和Bornitz模型对地铁运行引起地表各测点处1/3倍频程谱预测结果对比。由图10可知两种模型预测结果基本一致,可见两种预测模型均可较好地预测地表测点的1/3倍频程谱,表明两种模型预测的有效性。预测模型在低频段具有很好的吻合性,在高频段的部分点位具有一定的误差。由图7和图9可知,除特殊频率点外,对数衰减模型系数A和材料阻尼系数在低频段与频率具有较好的线性相关性,在高频处拟合效果相对较差。因此,对数衰减模型和Bornitz模型振级预测效果也体现类似规律,即低频预测效果好于高频。这可能与现场施工引起的高频振动干扰有关。
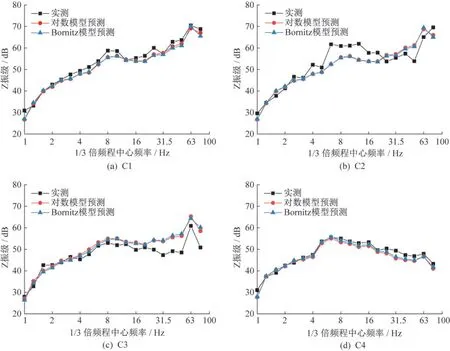
图10 对数模型和Bornitz模型预测不同位置1/3倍频程谱结果对比Fig.10 The comparison of 1/3 octave band spectrum between logarithmic regression model and Bornitz model
4 结 语
本文基于地铁运行引起的地表振动实测分析了加速度随距离的衰减规律,研究了对数衰减模型和Bornitz模型参数特性,并对比了两种模型预测振级的效果,初步得出的结论如下:
(1) 地铁列车引起的地面竖向振动优势频率和对应幅值均随着距离增加呈衰减趋势。在近轨道处高频振动占主导,在远轨道处低频振动占主导。
(2) Bornitz公式可较好预测地铁运行引起地表振动加速度峰值。近振源处两个水平方向上的加速度峰值显著大于竖向加速度峰值,随着距离增加,水平方向加速度峰值衰减速度快于竖向,并最终衰减至相当水平。这主要与地铁在曲线段上运行所产生的向心力有关。由本文结果可知对于曲线段地表水平加速度峰值可达竖向的3~4倍,因此对于曲线段需要特别关注水平向振动的影响。
(3) 对数衰减模型可以很好地拟合振级衰减与传播距离之间的关系。模型中的拟合系数A随着频率的增加也逐渐增大,表明振级的衰减速度随着频率的增加而增大。
(4) 基于Bornitz公式的振级预测模型也可较好预测地铁运行引起的地面振级。Bornitz公式中材料阻尼系数αM与频率具有良好的线性相关性。该场地的频率无关材料阻尼系数α0和阻尼比D范围分别为(0.146~0.522)×10-3s/m和(0.282~1.001)×10-2s/m,这与既有研究结果一致。

