改进的动力松弛法及其在张拉整体结构找形中的应用
郑亦汶 杨伟家 王贵祥 赵颖超 冯晓东,*
(1.绍兴文理学院土木工程学院,绍兴 312000; 2.浙江勤业建工集团有限公司,绍兴 312000;3.浙江交工集团股份有限公司,杭州 310002)
0 引 言
动力松弛法是一种从时间和空间两个维度离散来求解非线性结构静力问题的方法,最初由Otter提出并应用于求解潮汐流的计算问题[1]。1998年由Barnes[2]最早应用于解决索网及索膜结构的找形问题,因其算法收敛速度快、无需组装总刚节约内存、且对具有约束的结构形态改善问题以及求解索系非线性结构问题有着很好效果等特点而迅速受到大批学者关注[3]。在算法应用层面,单建和蓝天[4]运用动力松弛法对空间张拉结构的静力问题进行求解,并给出了该方法的两种稳定收敛条件。涂桂刚等[5]利用动力松弛法对树状结构单元集群进行了找形分析,成功的克服了树状结构找形的问题需要多次调整的弊端,同时有效减少了结构中的低效构件。董越等[6]对柔性结构施工过程开展模拟,采用动力松弛法对结构体系在张拉施工各阶段进行了非线性分析;在算法优化层面,伍晓顺和邓华[7]采用抛物线拟合的方法求解了精确的极值点位置,优化了常规动力松弛法在动能极值点处较为粗略的参数重置措施。但该方法并未能使运动精确回溯至所定位的极值点处,从而导致可能出现算法收敛不稳定的情况。苏小卒和王伟[8]通过求解时积分点应力的更新,提出一种基于动力松弛法迭代思想的非线性弹性增量算法,并利用相关算例验证了该方法在“依赖应变历史材料”(SHDM)结构非线性分析中的有效性。Rezaiee-Pajand等[9]根据多个研究对象针对性的给出了不同的参数组合方式,扩大了动力松弛法的应用范围。
综上所述,现有文献对动力松弛法的改进主要针对算法的原理部分,而对算法效率及稳定性的相关研究较为少见。但必须指出的是,利用动力松弛法处理较为复杂的结构形态问题时,时常会出现收敛效率较低甚至无法收敛的情况,这在一定程度上限制了该方法的应用场景。此外,尽管动力松弛法的应用已经非常广泛,基本涵盖了大部分索系结构以及预应力结构的找形问题和张拉施工阶段的模拟问题,但对于张拉整体[10-12]这种新兴的索杆自平衡结构则涉及较少。众所周知,找形分析是研究此类索杆柔性结构的基础[13],结构“找形”不仅需要寻找满足预期的几何形态,同时需确保寻找到可行预应力满足拉压分离的单边条件[14-16]。
本文针对常规动力松弛方法收敛效率较低及收敛不稳定等问题,提出了一种对动能极值点处坐标修正的方法,使运动追溯过程更加精确,改善算法收敛性能的同时扩大了算法收敛的区域。通过对两个张拉整体结构典型算例的找形分析,验证了本文算法在求解大型、复杂张拉整体结构找形问题中的准确性和有效性,同时为寻找其他复杂张拉整体的形态及预应力扩宽了思路。
1 动力松弛法的改进
1.1 动力松弛法的初始条件
以下初始条件需在问题求解前事先确定:
(1) 结构的初始几何构型及拓扑关系;
(2) 预设的结构初始预应力;
(3) 构件截面相关参数;
(4) 材料的本构关系(不考虑非线性)。
1.2 动力松弛法的基本原理
根据达朗贝尔原理,结构体系在任意时刻任意节点的力系需满足以下动力平衡方程:
结构阻尼c的形式大体可分为粘性阻尼和运动阻尼两种,在动力松弛法中采用了运动阻尼,因此ci=0。
根据中心差分法对加速度进行如下差分:
将式(2)代入(1)中,可得速度的递推公式:
单元内力的更新则可由更新的节点坐标求得:
节点不平衡力伴随着单元内力的变化而改变,可由力密度法求得[17]。循环迭代式(3)、式(4)、式(5),记录每次循环迭代中所有节点的总动能:
当结构体系总动能开始下降,则表明结构运动已越过动能极大值点(即势能极小值点),此时将结构运动过程回溯至极值点附近,重置所有节点速度为零,并以此为结构新的初状态开始下一次的循环,直至节点最大不平衡力趋向于零,最终得到一个满足平衡条件的结构。
1.3 动力松弛法的收敛性
Barnes[2]根据极限平衡条件得出动力松弛法的收敛条件如下:
式中:Simax为i节点的节点最大刚度;Mi为i节点的虚设节点质量;Δt为迭代时间步长。
对于索杆体系,节点最大刚度Simax表示为连接该节点所有单元的刚度系数之和,计算如下:
式中:k为连接i节点的单元总数;L0为单元的初始长度;Ln、Tn分别为单元当前时刻的长度和内力。
故为简化计算,令节点质量:
式(10)即为动力松弛法收敛需满足的稳定条件。
在此基础上,动力松弛法收敛性能的优劣仍受到诸多其他因素的影响。首先是试算,根据经典动力松弛法理论显示,当Δt取值大于力在结构节点间传递的最短时间时,算法是无法收敛的。因此采用动力松弛法进行计算时,需要事先选择一个时间步长Δt进行收敛性试算,算法无法收敛时则选择一个更小的时间步长Δt进行试算,以此类推,直至算法收敛。其次算法在动能极值点处定位与重置的准确性也会直接影响到算法的收敛性。最后是算法的收敛效率,在满足收敛条件情况下,动力松弛法的收敛效率往往与时间步长Δt成正相关,即Δt取值越大,算法收敛越快。综上所述,扩大Δt的可选范围不仅可以有效减少试算的工作量,且可以达到算法快速收敛的目的。
1.4 初始化动能极值点
如1.3节所述,动能极值点处的定位与重置是影响算法收敛性能的一个重要因素,本文将针对以上问题提出一种基于中心差分方法的极值点定位方法和基于有限差分法的节点坐标修正方法,以改善常规动力松弛法的收敛性能。
1.4.1 极值点的定位
本文认为,当计算过程中越过动能极值点后(t+Δt/2时刻动能小于t-Δt/2 时刻动能),极值点的落点区间存在以下两种情况,即落点区间(图1(a)、图1(b)中青色部分)分别为[t-Δt/2 ,t+Δt/2)和(t-3Δt/2,t-Δt/2],如图1所示。
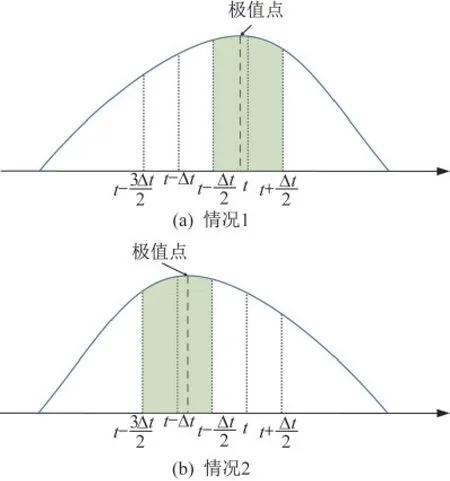
图1 极值点落点区间的两种情况Fig.1 Two cases of extreme point intervals
在动力松弛法中,无须过度追求极值点的精确定位,因为这并不会带来等效的性能提升,所以只需将运动过程回溯至极值点附近即可。结合上述极值点落点区间的两种可能,本文提出的极值点定位方法主要分为以下两个步骤:
(1) 根据中心差分法,分别求得t-Δt、t时刻的节点速度:
(2) 比较t-Δt、t-Δt/2以及t时刻三个时间点的结构总动能Ek,选取最大动能所对应的时刻作为极值点时刻。
值得注意的是,本方法在常规松弛法确定极值点的基础上,在极值点附近通过缩小时间步长的方式对总动能进行再次判断,提升了每次迭代的精度,但不可否认的是,由于每次迭代比常规算法多两个时间点,势必会增加部分计算量,从而牺牲一定的计算时长。但第三节中的相关算例结果可以证明,相比于算法精度的效果提升,此部分增加的算量影响甚小。
1.4.2 节点坐标修正
如前节所述,极值点定位的精确程度不会对整个算法流程产生太大影响,但极值点定位后的节点坐标修正则会直接影响到整个算法的收敛性能,因此极值点的定位应作为节点坐标修正的基础。通过1.4.1节所述方法进行极值点定位后,若t-Δt、t-Δt/2、t三个时刻的最大动能出现在t-Δt/2时刻,则对节点坐标进行如下修正:
动能最大值在t-Δt时刻,则进行如下修正:
1.4.3 改进的算法流程
改进的算法流程如下所示(图2):
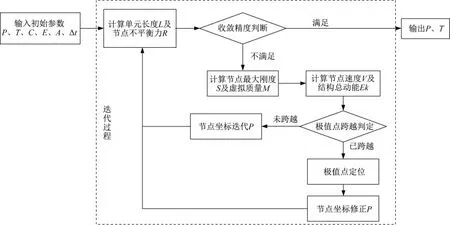
图2 改进的算法流程图Fig.2 Flowchart of the modified algorithm
步骤1:输入结构的初始信息,包括节点坐标P、初始预应力T、结构拓扑C、杨氏模量E、材料截面积A以及合适的运动步长Δt。
步骤2:通过初始信息计算节点不平衡力R。
步骤3:判断节点不平衡力R是否满足精度要求,满足,输出结果,算法终止;不满足则计算节点刚度S[式(8)]及节点虚拟质量M[式(9)]。
步骤4:根据节点不平衡力R通过速度递推公式求得速度及结构动能等[式(3)、式(6)]。
步骤5:动能大小比较判断,未越过动能极值点则计算节点坐标P并继续迭代步骤1~4;越过动能极值点则进行极值点的定位及节点坐标修正,随后重新开始运动,重复迭代直至节点不平衡力R满足精度要求。
2 算 例
本文通过以下几个算例对提出的改进动力松弛法进行有效性验证,并将其与常规的动力松弛法和文献[7]所述方法针对收敛过程、收敛效率以及收敛稳定性进行对比分析,以此凸显本文方法的改善效果。
2.1 三棱柱单胞找形分析
三棱柱张拉整体单胞(图3)是一个自应力模态为1的张拉整体结构(红色为压杆,蓝色为拉索),分别使用力密度方法[16]以及本文算法对其进行找形分析。由表1可知,以常规方法为标准,虽然本文方法和文献[7]方法的极值点定位方法计算效率略有降低,但由于差距均在毫秒级别以下,相比于精度提升的效果,实际计算过程的算量代价可忽略不计。
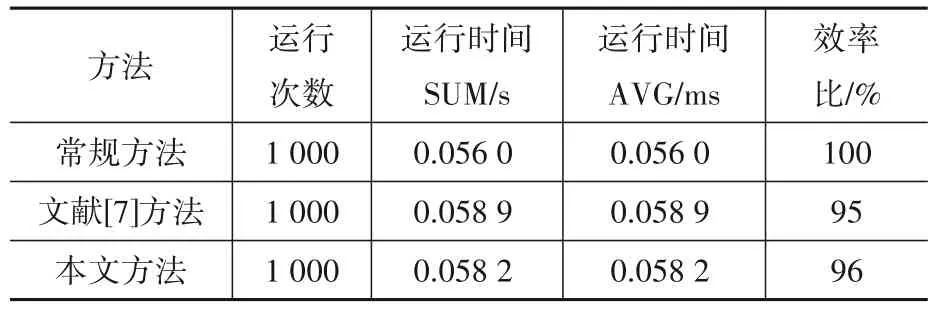
表1 不同定位方法的效率差异(三棱柱单胞)Table 1 Difference in efficiency of different methods(trigonometry tensegrity)
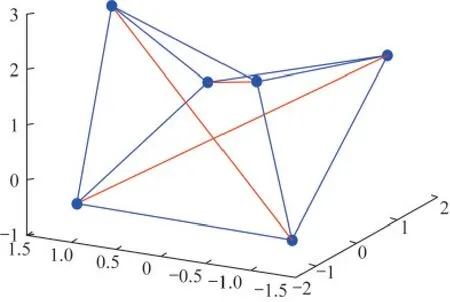
图3 三棱柱张拉整体单胞模型Fig.3 A cell model of trigonometry tensegrity
归一化后的力密度结果如表2所示,可见,本文算法结果与理论结果完全吻合。进一步的,在相同初始条件(Δt=0.7)和收敛条件(最大节点不平衡力≤1×10-6)的情况下,将本文方法分别与常规动力松弛法和文献[7]采用抛物线拟合的动力松弛法进行对比分析。
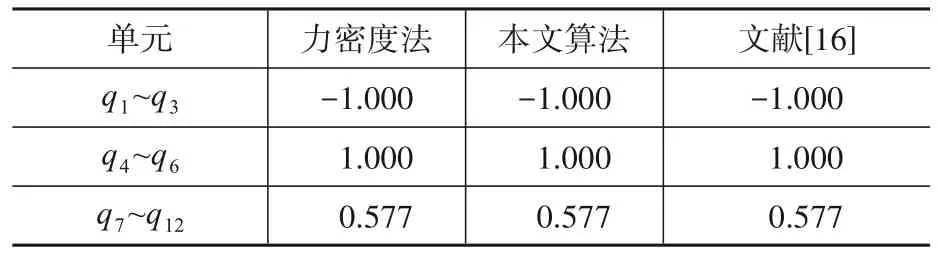
表2 力密度对比Table 2 Comparison of force density results
如表3所示,两种动力松弛法结果与本文算法结果完全一致,证实了本文方法的准确性。为进一步体现本文算法在收敛及稳定性方面的优势,图4给出了三种算法的详细迭代过程。

表3 不同动力松弛法结果Table 3 Results of different DR algorithms
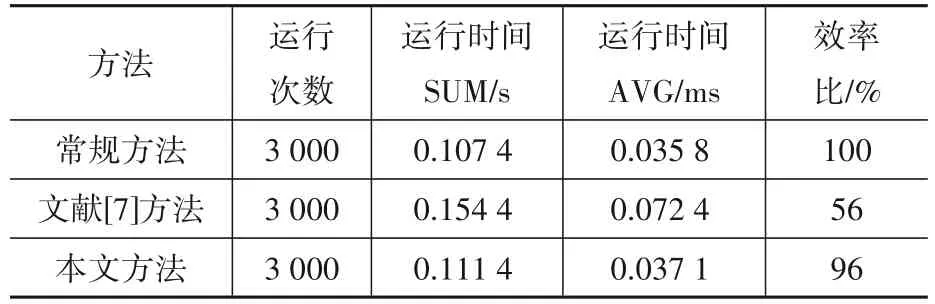
表4 不同定位方法的效率差异(六杆单胞)Table 4 Difference on efficiency of different methods(six struts tensegrity)
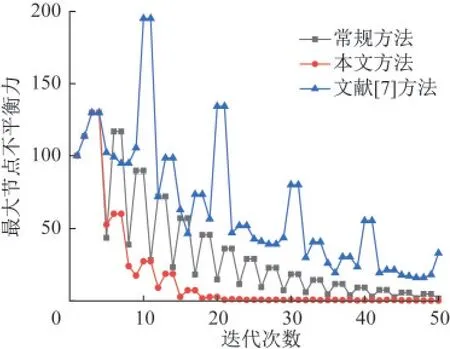
图4 算法迭代过程Fig.4 Iteration process of the algorithm
其中,运行时间(SUM)为运行1 000次极值点定位时的总计时长;运行时间(AVG)为平均每次进行极值点定位时所需要的时间;效率比为不同方法与常规方法进行极值点定位时运行时间的比值。
由上述结果可知,常规动力松弛法由于对极值点的判断较为粗略,结构运动无法回溯至势能极值点附近,故算法收敛较为缓慢;文献[7]采用的抛物线拟合求解极值点的动力松弛法虽可较为精确地对极值点进行定位,但因无法准确回溯至该极值点处,即无法对节点坐标进行修正,导致出现算法收敛过程波动较大、收敛较慢、迭代次数较多等问题。本算法通过中心差分方法对结构在极值点附近的运动进行精细划分,通过判断细分点处动能大小,进行节点坐标回溯修正,虽舍弃了较小部分极值点的精度,但极大提高了结构运动回溯的准确度。
2.2 六杆张拉整体结构的找形分析
为进一步展示本文算法的收敛效率及其在张拉整体结构设计中较强的找形能力,对一种由三棱柱单胞拼接组成的六杆张拉整体结构进行研究。
如图5所示,六杆张拉整体结构为由两个三棱柱张拉整体单胞通过上下底面中心点拼接而成的第一类张拉整体结构。现分别用三种动力松弛法对其进行找形分析,并以三种方法找形结果的方差作为找形结果的评价指标。

图5 六杆张拉整体模型Fig.5 Overall model of six-strut tensegrity

图6 本算法与现有方法的效率提升比较(六杆张拉整体结构)Fig.6 Comparison of efficiency improvement between the proposed algorithm and existing methods(six-strut tensegrity)
同样地,不同定位方法在处理不同数据量时的表现差异依然存在,但本文算法相较于常规方法的差距依然保持在毫秒级别以下。
如表5所示,在相同的初始条件(Δt=0.7)和收敛条件(最大节点不平衡力≤1×10-6)下,三种动力松弛法的收敛结果方差之和控制在4.61×10-17以内。在结果相同的情况下,对比常规方法和文献[7]方法,本文方法在收敛效率上分别提升了109%和198%。考虑到实际结构振动的复杂性,动力松弛法的迭代过程受到初始参数的影响较大,因此在保证其余条件不变的前提条件下,以0.01为间隔,仅针对时间步长Δt在0.01~0.7(文献[7]方法的稳定收敛阈值在0.7附近)区间内,收敛效率提升的百分比的对比。
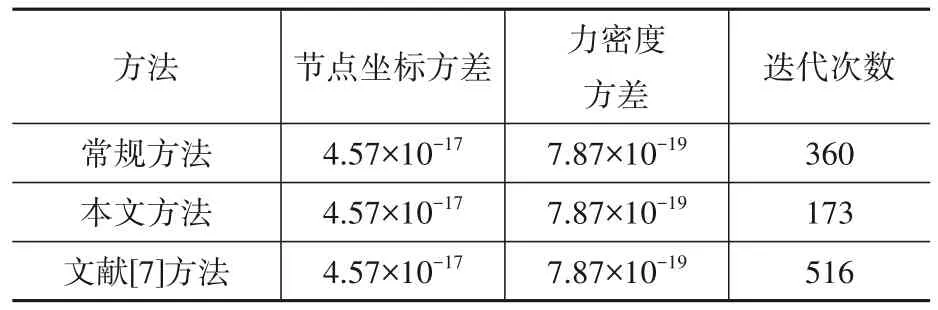
表5 六杆张拉整体结构找形结果Table 5 The form-finding results of six struts tensegrity
综上,相较于常规动力松弛法和文献[7]采用抛物线拟合极值点的动力松弛法,本文方法在此类张拉整体结构找形效率上有着较好地提升效果,并且设置的时间步长越大,提升效果也越明显。
2.3 螺旋塔型张拉整体结构找形分析
为验证本文算法求解大型复杂张拉整体结构找形问题的能力以及对动力松弛法收敛性能的改善效果,本文设计了一种螺旋塔型张拉整体结构并对其进行找形分析。该螺旋塔型张拉整体结构由三棱柱单胞之间通过上下底部中心点连接、旋转以及添加联系单元等操作组合而成(表6)。本文算法最终找形结果显示螺旋塔型结构的一个平衡构型是接近于广州电视塔(中部细、上下端粗)的一个形态,找形结果符合张拉整体结构压杆离散、拉索连续的要求,验证了改进的动力松弛法在解决复杂张拉整体结构找形中可行性。为更好地阐述本文算法在收敛性能上的优良表现,仍采用常规动力松弛法、文献[7]方法以及本文算法进行结果比对,分别从算法收敛效率以及算法收敛稳定性两个方面开展研究。

表6 螺旋塔型张拉整体结构设计Table 6 Design of spiral tensegrity tower
就算法收敛稳定性而言,表7所示为三种算法在不同时间步长的收敛情况(√为收敛,×为不收敛)。为了直观对比算法结果,若迭代次数超过2 000(本文算法收敛平均迭代次数为557)时仍未收敛则视为无法收敛。文献[7]方法的稳定收敛区间为时间步长0.01≤Δt≤0.71,即当Δt位于稳定收敛区间内时,则该算法收敛,反之则该算法无法收敛。同理,常规动力松弛法的稳定收敛区间为时间步长0.01≤Δt≤0.8,而本文方法在时间步长Δt≤1内可达到全域收敛。据表8结果可知,得益于计算机强大的运算能力,在面对较为复杂的张拉整体结构模型时,不同定位方法之间的计算效率未有明显差异。

表7 不同Δt步长的收敛情况Table 7 Convergence with different Δt
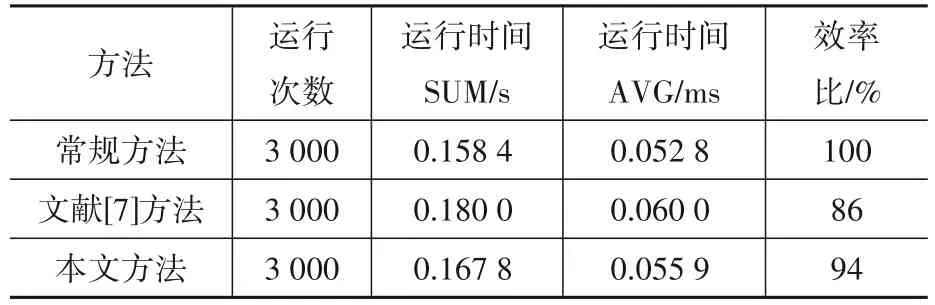
表8 不同定位方法的效率差异(螺旋塔张拉整体结构)Table 8 Difference in efficiency of different methods(spiral tensegrity tower)
因此在收敛稳定性方面,就该螺旋塔型张拉整体结构,本文方法的收敛稳定区间相对于常规方法和文献文献[7]方法分别扩大了25%和41%。值得一提的是,算法的收敛效率也是评判一个算法收敛性能优劣的重要指标。图7所示为三种方法在不同时间步长Δt下的迭代收敛情况。
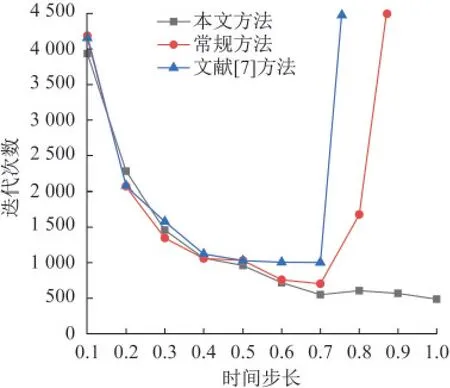
图7 三种方法的全局收敛表现Fig.7 The global convergence performance of three methods
由图7可知,随着时间步长Δt的增大,三种算法迭代次数呈下降的趋势,即收敛效率逐渐提高。在0.1≤Δt≤0.5时,三种方法收敛效率相差不大,从Δt=0.5附近开始,本文算法优势逐渐体现,随着时间步长的增大,迭代次数持续下降,算法收敛效率继续提高,而常规方法和文献[7]方法分别在越过Δt=0.8、Δt=0.71附近后出现迭代次数急速上升的情况,即算法无法收敛。同样地,为直观展示本文算法在收敛效率上的优势,假定常规方法与文献[7]方法在无法收敛情况下的迭代次数为2 000,收敛效率提升百分比曲线如图8所示。
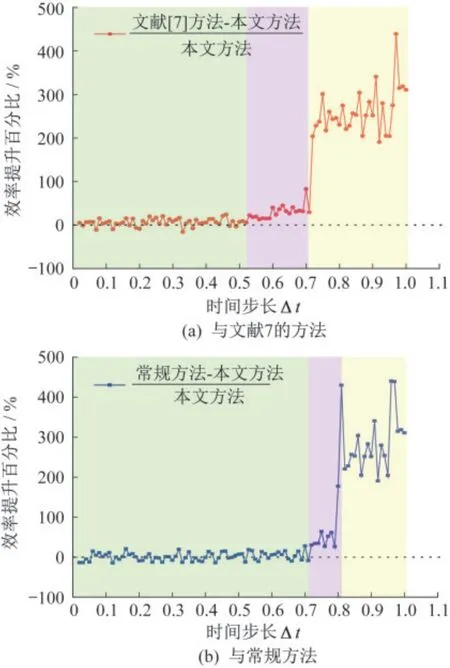
图8 本算法与现有方法的效率提升比较(螺旋塔型张拉整体结构)Fig.8 Comparison of efficiency improvement between the proposed algorithm and existing methods(spiral tower tensegrity tower)
图8(a)、图8(b)分别为本文方法相较于文献[7]方法和常规方法的收敛效率提升曲线。在稳定收敛区(绿色区域+紫色区域)中,小步长区域(绿色区域)三种方法的收敛效率差异并不明显。在大步长区域(紫色区域)内,本文方法相较于其余两种方法在收敛效率上均有着不同程度的提升。对比文献[7]方法,最高效率提升约为80%,平均效率提升约为30%。对比常规方法,最高效率提升约为177%,平均效率提升约为48%;在常规方法和文献[7]方法无法收敛的黄色区域,本文算法不仅能保持稳定收敛,而且收敛效率仍呈上升趋势。
综上,本文所提出的改进动力松弛法不但能很好应对大型、复杂的张拉整体结构找形问题,同时相较于常规动力松弛法以及文献[7]的动力松弛法在处理此类张拉整体找形问题时有着更好的收敛效率和更大的稳定收敛区域。
3 结 论
(1) 本文所提出改进方法能准确求解简单的三棱柱张拉整体结构找形问题,相对于常规动力松弛法和文献[7]的方法具有更好的迭代收敛进程。此外,常规动力松弛法能解决的问题,本文方法同样适用(例如索穹顶和弦支穹顶等空间索杆结构)。
(2) 本文算法在求解六杆张拉整体结构找形问题中,在结果相同的情况下,相较于其余两种方法收敛效率提升了17%~58%,最大提升198%。
(3) 针对大型的螺旋塔型张拉整体结构找形问题,本文算法相比于其余两种动力松弛法具有30%~48%收敛效率的提升,同时稳定收敛区域扩大了25%~41%。

