基于卷积神经网络和多变量递归图的斜拉桥拉索损伤识别

刘鹏飞 段元锋 段政腾

（浙江大学建筑工程学院，杭州 310058）

0 引 言

斜拉桥结构具有优越的跨越能力和经济性，因此广泛运用于跨江、跨河和跨海等重要的交通工程，有着重要的社会与经济意义。通常大跨桥梁结构的设计使用年限为100年，但由于其自身柔度大，阻尼小，实际运营过程中还承受着强风、地震和车辆荷载等动力荷载作用，桥梁构件很容易产生损坏。国内外很多学者开展了基于结构模态参数、模型更新和信号分析技术的桥梁结构损伤识别方法的研究，但桥梁健康监测系统的信号具有较强的非线性和非平稳性，制约了前述等方法的进一步发展。实际桥梁在运营期间除了承受自重和车辆荷载外，还会受到地震、强风、船撞和车辆超载等灾害威胁，难免会发生各种各样的结构损伤，桥梁的承载能力和耐久性也有一定程度的降低，不能满足设计使用年限要求，在极端情况下还会产生难以预计的灾难性事故［1-4］，造成严重的经济损失。因此，桥梁损伤识别一直是国内外学者的研究热点之一。

国内外学者针对桥梁损伤主要有基于模态参数、现代信号处理方法、优化方法和机器学习的损伤识别方法，但均存在各种程度的不足和局限性。

1） 基于模态参数的损伤识别研究

基于模态参数的损伤识别方法［5-6］是结构健康监测领域的经典内容，模态参数如频率、振型等是桥梁结构自身的特性，结构出现损伤时模态参数会发生变化。其优势是物理含义明确，解释性强，但实际使用时模态参数存在着易受环境因素影响，监测不完备，对局部损伤灵敏度低等问题。

2） 基于现代信号技术的损伤识别研究

桥梁结构出现损伤时，其监测信号的变化是非平稳的，现代信号分析技术［7-8］能够较好地刻画非平稳信号的局部特征，展示信号的全貌并保留瞬时特性。常用的信号分析技术有小波变换、短时傅里叶变换和HHT变换等，但是该方法在处理响应信号时存在着模态混叠问题，在实际复杂结构工程中的运用仍需进一步验证。

3） 基于优化方法的损伤识别研究

基于优化方法［9-10］的损伤识别方法的前身是基于模型更新的损伤识别算法，是典型的结构动力学反问题。该方法通过选择结构优化参数，构造目标函数，采用不同的优化方法如粒子群算法、遗传算法和模拟退火算法等，利用实际响应进行不断迭代求解，寻找到全局最优值时对应的结构参数，从而实现结构的损伤识别。但实际使用中监测得到的结构模态参数远小于待优化的结构模态参数数目，优化方法也无法考虑复杂的非线性行为和结构物理含义，结果容易出现陷入局部最优值，实际工程运用中存在较大的局限性。

4） 基于机器学习的损伤识别研究

基于机器学习的AI方法通过搭建机器学习模型使模型从数据样本中学习和提取特征，完成分类或回归任务。目前常见的基于机器学习的损伤识别方法［11-12］集中于采用加速度信号、模态参数等作为模型的输入，多用于简单模型的数值模拟与试验，也存在着识别精度不高且较少应用于复杂结构体系的问题。

采用的多变量递归图分析方法属于递归分析的研究范畴，为常规递归图的扩展形式。Eckmann等［13］于1987年正式提出了递归图的准确概念，是一个将一维信号转换成二维图像去观察信号递归行为的方法，展现状态空间中信号不同时刻状态之间的递归现象，被广泛运用于动力系统的分析。Zbilut等［14］提出了递归图量化分析的指标，如递归率、确定性、递归熵和递归趋势等。Nichols等［15］采用递归量化分析方法实现了铝薄板的损伤位置和损伤程度的识别，并讨论了递归图参数如阈值的选取。杨栋等［16］提出了基于递归图奇异熵的损伤识别方法，并通过简支梁数值模拟验证了该方法，得出了递归图奇异熵值随着损伤程度的增大而增大的结论，具有较好的敏感度。贾强辉［17］根据递归图中的平稳与非平稳模式对模拟信号进行定性分析，选择层状度（LAM）作为信号非平稳性及程度的评价指标，利用实测的桥梁振动信号来检验了层状度（LAM）评价指标的适用性和可靠性。

卷积神经网络属于深度学习方法的一种，最早由Lecun等［18］在1998年提出，通过堆叠多个隐藏层如卷积层、池化层和全连接层等，来模拟人脑的分层结构，实现输入样本的特征提取与特征映射，完成从输入样本到输出标签的分类或回归分析，例如其在人脸识别领域的精度已经超过人类平均水平。因此，拟结合递归图的非平稳信号分析能力和卷积神经网络优异的图片识别能力，首先提取斜拉桥数值模型不同损伤工况下的风致振动桥面加速度响应，接着选择合适的递归图参数，将加速度响应转换成二维的多变量递归图并赋予标签作为卷积神经网络CNN的训练和测试样本集，搭建卷积神经网络模型进行训练和测试，分析损伤识别结果，验证本方法的泛化能力和鲁棒性。

1 多变量递归图基本理论

1.1 递归图概念

递归图最早由Eckmann等［13］提出的针对非平稳、非线性信号的研究方法，对重构后的相空间中系统的运动轨迹的时间演化规律十分敏感，揭示结构动力系统的非平稳性和复杂度，算法具体流程如下：

1） 首先根据时间序列x={x1，x2，…，xn}重构其等价相空间如下：

式中：n为时间序列的长度，N为重构后X的长度；m为嵌入维度，τ为延迟时间，可分别通过虚假近邻法和互信息法求解。

2）在重构后的相空间X中，递归值Ri，j根据下式计算：

式中：Ri，j表示递归图在（i，j）处的值，ε为阈值，‖‖·表示欧几里得范数，Θ(·)为Heaviside函数，

3） 根据公式（2）可知，当Xi和Xj的距离小于阈值ε时，递归值为1，两相点间是递归的，在图中表示为黑点，反之，当递归图的值为0时，两相点之间无递归现象，在图上表示为白点。递归图沿着两条时间轴黑点和白点的组合会展现出不同的图像特征，反映时间序列x的递归特性。

选取相空间轨迹长度为1000，嵌入维度m为1，阈值为数据标准差σ，高斯白噪声、正弦信号和洛伦兹信号的递归图（图1）作为示例。

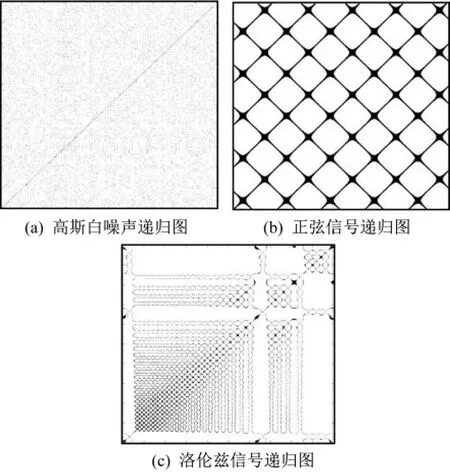
图1 三种不同信号的递归图Fig.1 3 different signals’ recurrence plot

三种不同信号的递归图分别对应递归图的三种基本模式：均匀模式、周期模式和漂移模式。这些基本模式的组合能够以二维图形的方式描述振动信号的特征。

1.2 多变量递归图

Nichols等［15］首次将多变量递归图用于结构健康监测领域中的损伤识别问题，通过分析多变量递归图的递归量化值，完成了薄板（0～25%）损伤程度的识别任务。实际桥梁健康监测系统中通常会布置多个不同点位的传感器（加速度、位移计、应变计等），以获得更加全面的桥梁结构信息。利用多个传感器的采集信号时序重构相空间从而得到多变量递归图，多变量递归图的构造公式如下：

式中：N为信号采样长度，n为传感器数目是第j个传感器在采样点i处的数据值。是相空间X′在时间点i处的相点，多个传感器的信号数据共同构成了相空间，同理选择合适的递归图参数后，根据公式（2）可以计算各相点的递归值后绘制多变量递归图。

1.3 斜拉索损伤时多变量递归图

斜拉桥有限元模型的原型是杭州市某斜拉桥缩尺的实验室模型（图2），主梁和主塔采用Beam188单元共628个，拉索采用Link10单元共40个，有限元模态分析结果如表1。对斜拉索引入损伤来开展研究，图2中斜拉索从左至右编号为C1-C20，对C3、C7、C9、C13、C15和C19斜拉索引入损伤。参考相关文献，改变弹性模量E变化来等效引入截面损伤，设定了单处拉索损伤和双处拉索损伤，损伤程度小于30%。采取Kaimal风谱模拟生成脉动风时程后计算抖振风力导入ANSYS模型进行动力计算，提取主梁上均匀分布的7个点位的加速度信号，不同损伤工况的多变量递归图如图3所示。

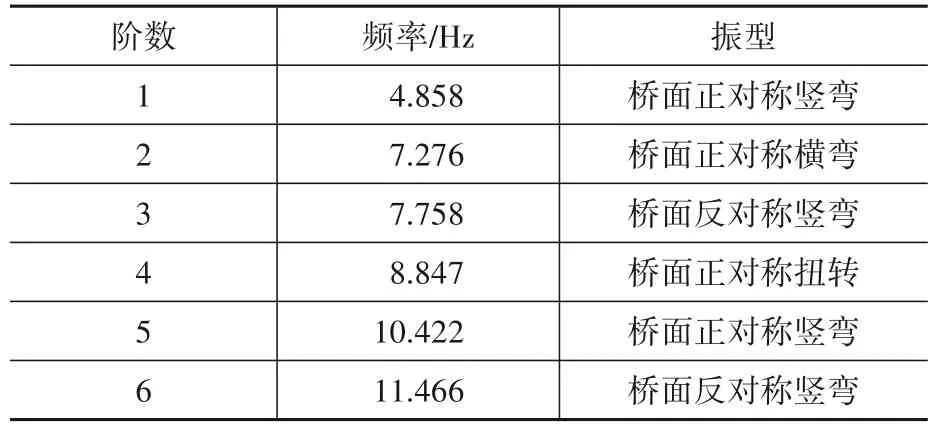
表1 斜拉桥有限元模型前6阶模态参数Table 1 Parameters of first 6 modals

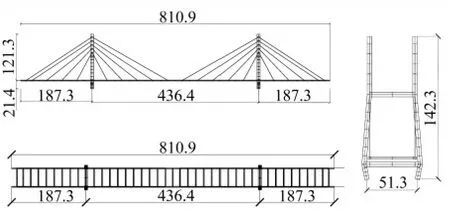
图2 斜拉桥模型图（单位：cm）Fig.2 Cable-stayed bridge model （Unit：cm）

图3 不同损伤工况的多变量递归图Fig.3 MRPs of different damage condition

根据图3可以看出，不同损伤工况的多变量递归图存在着整体差异和局部差异，当损伤程度增大时，多变量递归图的整体递归点会减小，即递归率下降；相同损伤程度但不同损伤位置时，递归图的左下和中部会呈现不同的突变细节信息；损伤引入导致结构模态参数发生改变，可以看出递归图的周期性也发生改变，如对角线结构的间距改变与消失，表明多变量递归图能够反映不同的损伤工况。

2 卷积神经网络搭建

2.1 卷积神经网络基本结构

卷积神经网络的经典结构（图4）为LeNet-5，包括输入层、卷积层、池化层（下采样层）、全连接层和输出层。

图4 卷积神经网络经典结构图Fig.4 Classical structure of CNN

2.1.1 卷积层

卷积层是完成特征提取的核心层，针对图像的二维卷积运算实例如图5所示。

图5 二维张量的卷积运算Fig.5 Convolution operation of 2-D tensor

2.1.2 池化层

池化层又被称为下采样层，一般设置于卷积层后，其目的是对卷积层提取出来的特征进行降采样，减少卷积神经网络的参数数量，提升网络的鲁棒性能，防止出现过拟合现象，不同的池化方式如图6所示。

图6 不同的池化方式Fig.6 Different pooling methods

2.1.3 全连接层

全连接层（图7）又被称为线性层，一般用于卷积神经网络的最后映射部分，将卷积层和池化层提取出来的特征映射到目标空间中，输入为特征，输出是预测结果。

图7 全连接层Fig.7 Fully-connected layer

2.1.4 激活函数

激活函数的主要作用是给卷积神经网络提供非线性建模能力，每次卷积运算结束后进行激活函数的运算，常用的激活函数有Sigmoid，Tanh，Relu和Softplus等。

2.1.5 损失函数和优化器

全连接层最后一层的输出将作为损失函数的输入，计算样本输出值和样本标签的误差。在深度学习中常用的损失函数有交叉熵函数（Cross Entropy）和均方误差函数（MSE），对于分类问题，一般采用交叉熵函数，反应两个概率分布的距离；对回归问题一般采用均方差函数来反应模型预测值和样本标签值的欧氏距离，分别如式（4）和式（5）所示。

式中：fij指的是第i个样本对应第j个类别上的标签值；yij是第i个样本对应第j个类别的预测值；Ji为第i个样本的代价函数值。

2.2 卷积神经网络模型

多变量递归图的输入尺寸为［1，2 048，2 048］，为单通道的黑白多变量递归图，输出层的大小为1×6，该向量的每列数值代表顺序位置（C3、C7、C9、C13、C15、C19）的斜拉索损伤程度，搭建的卷积神经网络的结构如表2和图8所示。

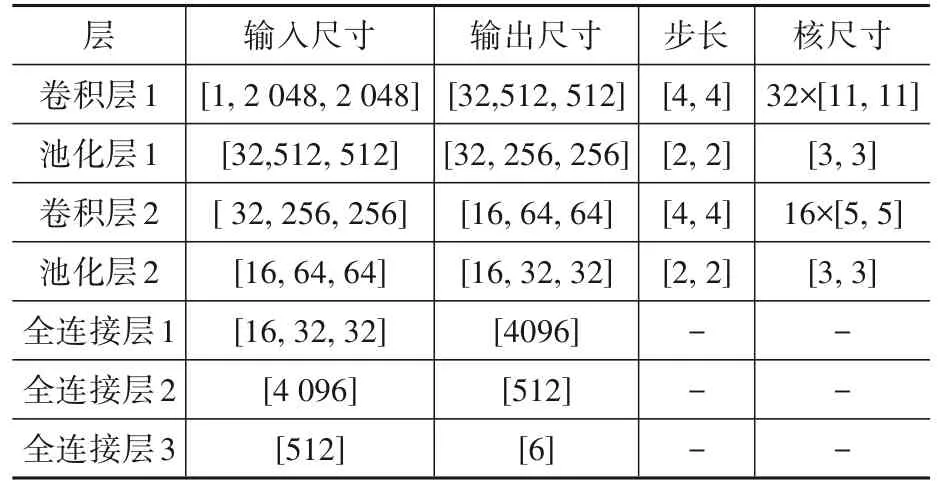
表2 卷积神经网络参数Table 2 Parameters of CNN

表3 训练集、验证集和测试集Table 3 Training， validation and test set

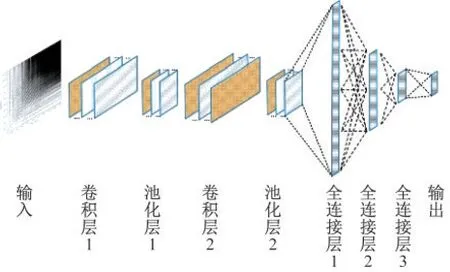
图8 卷积神经网络模型图Fig.8 Model structure of CNN

2.3 卷积神经网络优化方法

2.3.1 批归一化

批归一化法［19］可以有效解决神经网络训练时可能出现的梯度消失问题，还可以增强卷积神经网络的鲁棒性。训练集在进行训练时会进行随机打乱，因此每一批次的数据分布都可能存在不同，测试集同理也存在着不同的数据分布现象。

2.3.2 随机失活

随机失活［20］（Dropout）又被称为丢弃层，在卷积神经网络训练过程中按照一定的百分比随机忽略或者屏蔽一些神经元，这些神经元被随机抛弃了，因此其不会对后续的神经元有参数传递，在损失值通过梯度进行反向传播时该神经元的权重也不会更新。

2.3.3 早停法

早停法［21］（Early Stopping）是一种被广泛使用的避免模型过拟合的训练方法，训练时训练集的误差一般会不断减小，但验证集的表现可能会出现下降，这时候如果提前停止训练能够避免模型继续训练产生的过拟合现象。

3 斜拉桥损伤识别结果

3.1 训练集、验证集和测试集

将深度学习中CNN从样本数据中生成模型的过程称为训练，训练过程中采用的样本数据集称为训练集；训练集中留出20%比例的样本用于调优的样本数据集称为验证集；用来评估卷积神经网络泛化能力的数据集合称为测试集。为了生成卷积神经网络对应的样本数据库，并考虑到ANSYS模型计算时间、泛化性能和抗噪性能研究，针对每个工况10倍生成多变量递归图样本，在训练集中随机采用平均风速为5 m/s，8 m/s和10 m/s，损伤程度为10%，20%，30%，无损伤工况样本数量增加6组即70个，因此训练集样本数量为1 600。为了确保测试集生成的独立性，采用两种不同平均风速的脉动风时程测试集，测试集1的随机平均风速为5 m/s，8 m/s和10 m/s，损伤程度为5%，15%，25%，数量为1 530。测试集2的随机平均风速为7 m/s，9 m/s和15 m/s，损伤程度为5%，15%，25%，数量为1 530。

3.2 单处损伤识别结果

单处损伤识别结果如图9所示。

图9 单处损伤结果示例Fig.9 Single damage case results

此外，用准确度（Precision）和召回率（Recall）来评价模型的损伤识别精度，单处损伤程度达15%时结果如表4所示。

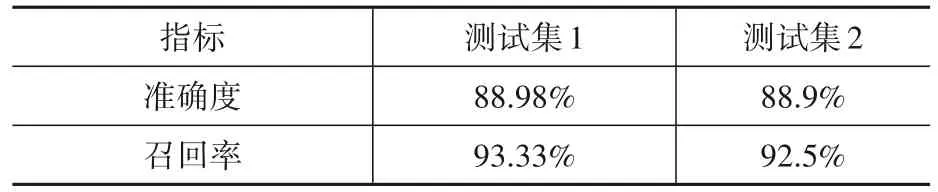
表4 测试集单处损伤位置识别结果Table 4 Singles damage location results of test sets

3.3 多处损伤识别结果

双处损伤时损伤结果示例如图10，双处损伤位置识别结果如表5所示。工程中更关注的指标为召回率，确保能够查找全面的损伤位置，表4和表5结果可以看出，召回率均高于90%，具有较高的损伤识别精度。

表5 测试集双处损伤位置识别结果Table 5 Two-damage location results of test sets

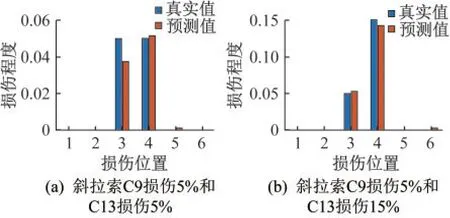
图10 双处损伤结果示例Fig.10 Results with two damage locations

针对三处以上位置的损伤，增加对应损伤工况的训练样本，调整卷积神经网络的结构参数和输出参数，本文损伤识别方法同样适用。

4 结 论

提出的基于多变量递归图和卷积神经网络的斜拉桥拉索损伤识别方法，一方面利用多变量递归图对监测信号的非平稳性分析能力和特征提取能力，另一方面利用卷积神经网络优异的图像识别能力完成不同工况的损伤识别，可以得出如下结论：

（1） 多变量递归图采用多条响应信号重构相空间，将响应信号的特征通过递归图表示，完成响应信号的非平稳性分析，充分提取响应信号的特征。

（2） 将多变量递归图作为卷积神经网络的输入进行训练与测试，损伤识别结果表明，单处损伤程度达15%时，损伤位置的召回率均高于90%，准确率高于88%，具有良好的损伤识别结果。