单项J-自伴向量微分算子谱的离散性与其系数的关系

钱志祥，林秋红

(广东理工学院 基础教学部，广东 肇庆 526100)

0 引言

随着Hamilton算子谱分析和算子逆谱问题研究的迅速发展，向量值微分算子谱理论引起了学者的广泛关注.向量值微分算子是Weidmann[1]首次引入的，他详细研究了对称向量微分算子的自伴随扩张理论及其谱理论.关于向量函数空间中微分算子的研究较少，特别是如何利用向量微分算子的系数来确定它的谱[2].J-自伴向量微分算子是向量函数空间中的微分算子，它常出现于能量耗散的量子力学系统[3]，一般是在研究非封闭动力系统时产生的[4-6]，它在系统理论、非线性分析和发展方程中得到了广泛的应用.

在纯量函数空间中，关于2N阶单项自伴微分算子谱的离散性与其系数的关系，早在20世纪50年代，Glazman[7]已经得到了2N阶单项自伴微分算子谱离散的一个充分条件，但它的谱离散的必要条件是一个世界难题，这个问题一直困扰数学界20余年，直到1974年，Lewis[8]终于解决了这个著名问题.2001年，王忠等[9,10]研究了单项J-自伴情形下的微分算子，得到了这类算子谱的离散性与其系数之间的关系，给出了单项J-自伴算子的谱离散的一些充分条件和必要条件.

在向量函数空间中，这类算子谱的离散性研究成果目前还很少见，2018年，钱志祥等[11]研究了自伴向量情形下这类算子谱的离散性，得到了该类算子谱离散的充要条件.本文研究二阶单项J-自伴向量微分算子谱的离散性.

考虑二阶单项微分表达式

其中，系数P(x)=P1(x)+iP2(x)是一个m×m阶复对称矩阵函数，P1(x)和P2(x)为m×m阶实对称矩阵函数.

本文研究微分表达式(1)在其J-自伴域内生成的J-自伴向量微分算子谱的离散性与其系数之间的关系.令y(x)=(y1(x),y2(x),…,ym(x))是定义在[0,+∞)上的m维向量函数，记λ1(x),λ2(x),…,λm(x)是实对称矩阵P1(x)的m个连续特征根函数，θ1(x),θ2(x),…,θm(x)是实对称矩阵P2(x)的m个连续特征根函数；λmin(P1(x))=min{λ1(x),λ2(x),…,λm(x)}和θmin(P2(x))=min{θ1(x),θ2(x),…,θm(x)}分别表示实对称矩阵P1(x)和P2(x)的最小特征根函数.

1 预备知识

定义1[10,12]定义算子T,T0如下:

其中

定义域中的f[i]是f(x)的第i阶拟导数，定义为

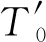
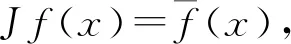
引理1[13]设算子A是一个闭的J-对称向量微分算子，且具有有限亏指数，即

def(A)=d<+∞,D(A)⊂D⊂D(JA*J),

D是A的J-自伴扩张的定义域的充分条件是：存在{w1,w2,…,wd}⊂D(JA*J)，使得

1){w1,w2,…,wd}模D(A)线性无关;

3)D={u∈D(JA*J):u,wjm=0,j=1,2,…,d}.

以下记σ(T)为算子T的谱，σr(T)为算子T的剩余谱，σc(T)为算子T的连续谱，σp(T)为算子T的点谱，σd(T)为算子T的离散谱，σe(T)为算子T的本质谱.

引理2[12]J-自伴算子T的剩余谱为空，即

引理3[12-14]设算子A是一个Hilbert空间上稠定的闭线性算子，如果λ∉{(Af,f):f∈D(A),=f==1}，那么λ∈Π(A)，这里Π(A)是算子A的正则型域.

引理4[13]若算子T是定义在Hilbert空间H上的J-自伴算子，则算子T的正则集和正则型域相同，即ρ(T)=Π(T).

引理5[7,12]具有有限亏指数的对称算子T0的所有自伴扩张T具有相同的本质谱，而且等于对称算子的本质谱.

引理6[15]若算子A是自伴算子A1,A2的直和，则A=A1⊕A2是Hilbert空间X上的一个自伴算子，而且

引理7[10,16]设A是Hilbert空间H的稠定闭线性算子，若A的预解算子全连续，则A的谱是离散的；若A是自伴算子，则上述结论的逆也成立.

引理8[10,17]设L1,L2是Hilbert空间H中的稠定闭线性算子，且满足下列条件：

(a)L1,L2是对称的、半有界算子；

(b)D(L1)=D(L2);

(c)对某个复数λ0，集合R(L1+iL2-λ0I)或者R(L1-iL2-λ0I)在Hilbert空间H内是稠定的；

(d)对称算子L1+L2的Friedrichs扩张算子的预解算子是全连续的.

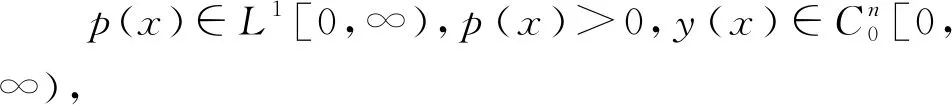
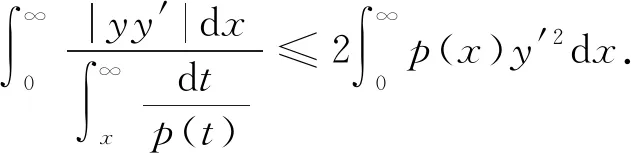
(2)

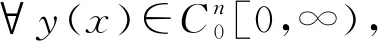
(3)

引理11[18](Weyl 特征值比较定理) 设矩阵A,B∈Cm×m是Hermitian矩阵，并且它们的特征值按增序排列，即有

则

其中，k=1,2,3,…,m.

引理12[7]设a[u,v]是稠定、闭、对称、下半有界的双线性型，则存在唯一的一个下半有界的自伴算子A，具有如下特性：

1)a[u,v]=(Au,v),u∈D(A),v∈D(a),D(A)⊆D(a);

2)D(A)在距离=·=a之下在D(a)内稠密;

3)对∀v∈D(a),w∈X,a[u,v]=(w,v)成立，则u∈D(A)且Au=w;

4)若干a[u,v]≥0,u∈D(a)，则D(a)=D(A1/2)且a[u,v]=(A1/2,A1/2),u,v∈D(a).

引理13[15]设a[u,v],b[u,v]是两个稠定的、闭的、对称的、下半有界的双线性型，而且a[u,v]≥b[u,v],u∈D(a)⊆D(b).设A,B分别是由a[u,v],b[u,v]生成的自伴算子，若σe(B)∩(-∞,λ)=∅,-∞<λ≤∞，则σe(A)∩(-∞,λ)=∅.

引理14[7]若

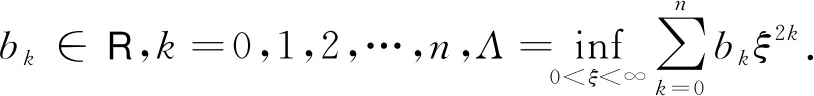
2 谱的离散性的充分条件

定理1当向量微分表达式(1)中的系数矩阵P(x)=P1(x)+iP2(x),x∈[0,∞)的实部P1(x)和虚部P2(x)均取值为正定对角矩阵时，即

则向量微分表达式(1)在其J-自伴扩张域内生成的算子L是一个J-自伴算子，它的所有J-自伴扩张算子的谱离散的充分条件是

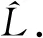
由定义1，可设L1,L2,L分别表示由微分表达式τ1,τ2,τ生成的最小算子，即

下面只要证明算子L1,L2和L满足引理8的条件，然后再根据引理7就可以得出结论.

根据表达式(8),(9)及实部矩阵和虚部矩阵的正定性可知，算子L1,L2是对称的稠定算子且D(L1)=D(L2).对于∀y∈D(L1)=D(L2)，考察二次型，并利用分部积分可得

所以

同理可得

因此算子L1和L2是下方有界的，于是算子L1和L2满足引理8的条件(a)和(b).

由(8)～(12)式，设L=L1+iL2，因为算子L是一个J-自伴算子，根据引理2知

σr(L)=∅,σ(L)=σd(L)+σe(L).

根据引理4可知Π(L)=ρ(L)，这里ρ(L)表示算子L的正则集，Π(L)={λ∈C:∃kλ，使得对∀f∈D(L),=(L-λI)f=≥kλ=f=}是算子L的正则型域.由引理3知，C=Π(L)∪σ(L)，因此算子L的正则集非空.若Reλ<0，则λ∈ρ(L)，所以算子L的预解集非空，并且集合R(L1+iL2-λI)或者R(L1-iL2-λI)在Hilbert空间H中稠定，这样算子L1,L2满足引理8的条件(c).

再设L′y=(L1+L2)y=(τ1+τ2)y=-((P1(x)+P2(x))y′)′,∀y∈D(L1)=D(L2)，显然L′=L1+L2是对称、稠定、下方有界的.接着证明算子L′的任意自伴扩张的谱是离散的.因为定理中的极限条件(5)成立，即对于给定的任意小的正数ε，总存在一个充分大的数N，使得当x≥N时，有

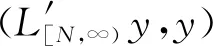
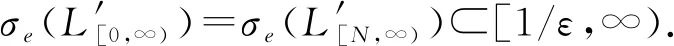
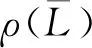
定理2当向量微分表达式(1)中的系数矩阵P(x)=P1(x)+iP2(x),x∈[0,+∞)的实部P1(x)和虚部P2(x)均为m×m阶正定对称矩阵时，记λi(x)(i=1,2,…,m)是实对称矩阵P1(x)的m个连续的特征根函数，θi(x)(i=1,2,…,m)是实对称矩阵P2(x)的m个连续的特征根函数.则向量微分表达式(1)在其J-自伴扩张域内生成的算子L是一个J-自伴算子，它的所有J-自伴扩张算子的谱离散的充分条件是

证明因为矩阵P1(x)和P2(x)都是m×m阶正定对称矩阵，故存在正交矩阵C1(x),C2(x)，使得

其中

证明过程类似于定理1，所以我们只给出不同的部分.设L1,L2,L分别表示由微分表达式τ1,τ2,τ生成的最小算子，同样只要证明L1,L2,L都满足引理8的条件(a)～(d)即可.

满足条件(b)和(c)的证明和定理1相同，下面只证满足条件(a)和(d).分部积分结合系数矩阵的正定性可知，对于∀y∈D(T10)=D(T20)，有下列关系式：

同理可得

所以，算子L1和L2是下方有界的，这样L1和L2满足引理8的条件(a).

下面再证算子L1和L2满足引理8的条件(d).对于∀y∈D(L1)=D(L2)，设L′y=(L1+L2)y=(τ1+τ2)y=-((P1(x)+P2(x))y′)′，那么算子L′=L1+L2是对称的、稠定的、下半有界的算子.利用定理的条件(14)，对于给定任意小的正数ε，存在一个充分大的数N，使得当x≥N时，有

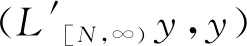
其中

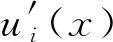
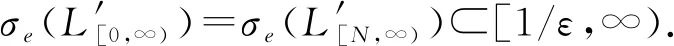
综上所述，算子L1,L2和L满足引理8的条件(a)～(d)，于是定理得证. 】

定理3当向量微分表达式(1)中的系数矩阵P(x)=P1(x)+iP2(x),x∈[0,+∞)的实部P1(x)和虚部P2(x)均为m×m阶正定对称矩阵时，记λi(x)(i=1,2,…,m)是实对称矩阵P1(x)的m个连续的特征根函数，θi(x)(i=1,2,…,m)是实对称矩阵P2(x)的m个连续的特征根函数.则向量微分表达式(1)在其J-自伴扩张域内生成的算子L是一个J-自伴算子，它的所有J-自伴扩张算子的谱离散的充分条件是

证明由定理2立刻证得. 】

定理4当向量微分表达式(1)中的系数矩阵P(x)=P1(x)+iP2(x),x∈[0,+∞)的实部P1(x)和虚部P2(x)均为m×m阶正定对称矩阵时，记λi(x)∈L1[0,+∞),i=1,2,…,m是实对称矩阵P1(x)的m个连续的特征根函数，θi(x)∈L1[0,+∞),i=1,2,…,m是实对称矩阵P2(x)的m个连续的特征根函数.则向量微分表达式(1)在其J-自伴扩张域内生成的算子L是一个J-自伴算子，它的所有J-自伴扩张算子的谱离散的充分条件是下列两个条件成立：

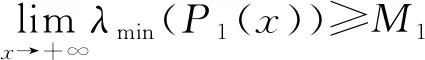
(ii)下面公式成立：

证明证明过程与定理2相似，稍作修改即可证得. 】

3 谱的离散性的充分必要条件

定理1中，如果对系数矩阵P1(x)和P2(x)的特征根函数加以一定的限制条件，我们也能给出这类算子的谱离散的一个充分必要条件.

定理5设向量微分表达式(1)中的系数矩阵P(x)=P1(x)+iP2(x),x∈[0,+∞)的实部P1(x)和虚部P2(x)均为m×m阶对角矩阵，即

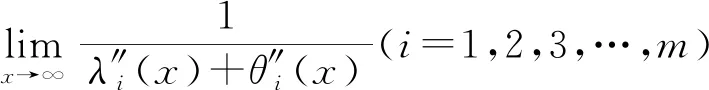
利用洛必达法则可得

所以

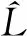
其中

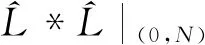
为了方便，记

所以

利用(27)～(29)式可得

取N充分大，则存在实数Ci>0(i=1,2,3)，使得

设

则a[y,z]是一个闭的、下方有界的双线性型，根据引理12，存在自伴算子A，使得a[y,z]=(Ay,z)，它是一个欧拉算子.根据引理14知，算子A的本质谱σe(A)=[Λ,∞)，其中

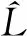
由直和分解定理可知

根据(35),(36)式和引理13得到σe(A)∩(-∞,+∞)=∅，所以算子A的本质谱为空，即σe(A)=∅，但是欧拉算子的本质谱σe(A)=[Λ,∞)，这显然是一个矛盾，因此假设错误，条件(22)式成立，必要性得证.】

4 应用

例1当向量微分表达式(1)中的系数矩阵P(x)是一个m×m阶复矩阵时，记

如果ai>0,bi>0,max{αi,βi}>2(i=1,2,…,m)，那么算子L的所有J-自伴扩张算子的谱是离散的.

证明因为题设满足定理1的条件，所以结果成立. 】

例2设向量微分表达式(1)中的系数矩阵

证明因为满足定理5的所有条件，故结论成立. 】

J-自伴向量微分算子理论在量子力学的能量耗散问题、反散射、逆谱等问题中有着广泛的应用，热传导、流体力学、机械振动系统和复信号处理系统中的许多微分方程一般都可以转化为J-自伴向量微分算子问题来求解，因此研究J-自伴向量微分算子谱的离散性对于求解微分方程具有重要理论意义.值得思考的问题是：高阶情形下的J-自伴微分算子谱离散性的必要条件至今尚无结果.