太阳能热发电系统多模型加权预测控制研究

丁 坤，孙亚璐，杨昌海，陈博洋

(国网甘肃省电力公司 经济技术研究院，甘肃 兰州 730000)

太阳能光热发电与其它的新能源发电方式相比，其与现有电网的匹配性更好，可直接上网，且能实现规模化的生产，因而受到了广泛关注.要保证稳定的发电量，控制的关键是利用太阳辐照强度加热循环流动的熔盐，使集热场熔盐的出口温度控制在一定的范围内[1-3].因此，多种智能控制算法在此得到了应用，其控制的目的是减小跟踪误差，使得集热器的出口温度控制在一个相对平稳的范围内.Len等[4]针对线性菲涅尔集热场设计了一种自适应模型预测控制器，仿真结果与PID+前馈串联控制器和GS-GPC策略相比较，均有较好的跟踪性能；Lima等[5]利用滤波动态矩阵对太阳能集热场的输出温度进行控制，与动态矩阵控制相比，提高了系统的鲁棒性和抗干扰性；Lu等[6]提出了基于卡尔曼滤波器的模型预测控制，进一步提高了集热系统的稳定性；Gil等[7]介绍了一种在分布式太阳能集热器领域基于约束仿射状态空间神经网络的预测控制方案，用状态空间非线性模型的阶数来度量神经网络预测器的复杂度，通过估计数据驱动Hankel矩阵的子空间斜投影的主奇异值个数来处理，该神经网络首先离线训练，随后通过基于双无迹卡尔曼滤波器的递归更新权值和偏差来改进，抑制了太阳辐射强度变化对系统的影响；张志勇等[8]提出了基于K-means方法的径向基函数(Radial Basis Function, RBF)神经网络温度预测模型，仿真结果表明，该模型可以有效实现线性菲涅尔集热回路出口熔盐温度预测输出，这一模型已应用于敦煌50MW熔盐线性菲涅尔式光热示范电站的实际运行中，指导电站集热回路出口温度的预测控制.

现有的对太阳能光热发电集热场出口温度的控制大多采用模型预测控制算法，且都是采用单模型为预测模型；聚类多模型预测控制已成功应用于其它随机性强的系统的控制中[12-14]，已取得了较好的效果.文中基于以上分析，主要研究内容包括：

1)采集2500组太阳能集热数据组，采用模糊聚类算法对数据组进行有效分类，采用遗忘因子递推最小二乘法建立多变量预测模型.

2)以入口熔盐温度、太阳辐照强度以及环境温度为扰动信号，集热管内熔盐的流量为控制量设计多模型.

3)针对每个子模型设计相应的控制器，根据系统工作状态的变化选择不同的子模型，再对子控制器采用一定的加权策略不断更新得到最小的控制增量，将MMPC控制应用到实际的线性菲涅尔热发电系统中，和SMPC结果进行对比分析，结果说明：MMPC控制精度高于单模型，系统控制的平稳性更好.

1 集热系统的动态数学模型

Carmona等[9]首次对太阳能集热子系统的数学模型进行描述，在集热器工作的过程中，吸热管表面吸收的热量加热流动的熔盐，使得管内熔盐的温度升高，将吸热管分成N等分，每一段用Δx表示，则可以得到

吸热管吸收的热量一部分被吸热管内熔盐吸收，一部分散失到大气中，可以得到

将(1)式和(2)式合并，可以得到

(1)～(3)式中：n∈[1,N]；Tab为吸热体温度；Tair为外界环境空气温度；Kab-f为从吸热体到流体的综合传热系数；Kab-air为从吸热体到环境空气的综合传热系数；t为时间；Δx为集热集热管分段；m,ρf为工质密度和比热容；Af为管道横截面积；u(t)为熔盐流量；I(t)为太阳辐照强度；η0,G1分别为反射镜光学效率和光学孔径；Tout,Tin分别为集热管熔盐出口温度和入口温度.

真空吸热管吸收的热量绝大部分被吸热管内熔盐吸收，对于玻璃管管壁与空气的对流传热，环境温度对其传热具有明显的影响.对于金属内管与熔盐介质的对流传热，熔盐介质温度对其传热具有明显的影响.分析可知，影响出口温度的主要因素有太阳辐照强度、环境温度、集热场入口熔盐温度.因此，集热系统的输入输出关系为

Tout=f(I(t),Tin(t),Tair,η0,u(t)).

(4)

2 太阳热发电集热系统聚类建模

2.1 数据集模糊聚类

取实测的数据用聚类算法进行分类，再利用遗忘因子最小二乘辨识法生成多模型.模糊C均值聚类算法根据隶属度确定每个数据点的类别，当模糊目标函数最小时，把数据组分成c个模糊类，步骤如下：

1)首先确定类别数c和模糊权重指数m；

2)初始化聚类中心vj；

3)确定个体xi属于第j类的模糊隶属度uij：

其中，vj为第j类的聚类中心；

4)计算vj：

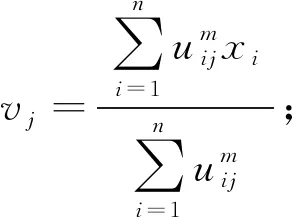
(6)

5)计算聚类目标值J1：

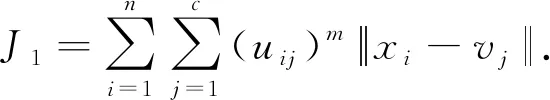
(7)

当J1最小时聚类结束，否则返回第2步.

2.2 聚类的有效性

采用指标D(Davies Bould,DB)对聚类的优劣进行判断，D用下式计算得到：

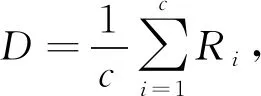
(8)

其中

这里，s(ci)为类内的紧密性度量；d(ci,cj)为类间距离.s(ci)和d(ci,cj)分别定义为

指标D是从类的平均相似性和几何的角度去考虑聚类的效果，D越小表示聚类效果越好.

文中取已经投入并网运行的兰州大成菲涅尔热发电的2500组数据进行分类建模，数组用S[s1,s2,s3,s4,s5]表示，其中，s1为出口温度，s2为入口温度，s3为导热熔盐流量，s4为太阳辐射，s5为环境温度.用模糊聚类分析，当聚类数等于5时D最小，表1列出了聚类结果.

表1 聚类结果

聚类中心为

2.3 最小二乘建模

根据数据分类的结果用遗忘因子递推最小二乘法建立集热器的数学模型，将入口温度、太阳辐射强度和熔盐的流量作为输入，出口温度为输出，为了克服最小二乘法修正能力差的缺点，采用遗忘因子递推最小二乘法，取性能指标为

遗忘因子递推最小二乘法的参数估计为

其中，θ(k)为待辨识的参数；K(k)为增益矩阵；φ(k)为观测矩阵；P(k)为协方差矩阵；λ为遗忘因子(0<λ≤1)，L为观测次数.

根据实测的数据和太阳能热发电聚光集热子系统运行的特点，采用(12)式表示的CAR模型对参数θ(k)进行辨识，结合数据分类结果，建立5个数学模型：

Y(k+1)=φT(k)θ(k),

(14)

其中

取初值θ(0)=0,P(0)=105I,λ=0.95，得到太阳能集热系统的5个数学模型如下:

其中，yi(k)为出口温度；ui(k)为熔盐流量；Tin1(k)为入口温度；Ii(k)为太阳辐射强度.(15)式可作为Tair(k)系统的预测模型.

3 多模型预测控制器设计

3.1 局部预测控制器

定义单变量MPC的性能指标[13-17]

其中，Nn为控制时域；N为预测时域；R(j)为控制增量的惩罚权矩阵；Qj为k+1时刻输出误差.各个子模型均为局部有效，每个子模型都有相应的有效域Γi，根据聚类中心可以确定.因此子模型的局部约束可表示为

Γimin≤φ(k+j)≤Γimax,

(17)

其中，Γimax和Γimin为有效域Γi的上下界，

φ(k)=(y(k)u(k-1))T,j=1,2,…,N.

因此局部约束可表示为

其中

局部模型同样应满足全局约束，全局控制增量的约束为

(18)和(19)式合并化简可以得到局部模型的约束预测控制问题

3.2 控制器的加权原理

控制器加权多模型预测控制器的设计准则为模型的调度函数值等于控制器的加权值，对各调度函数进行归一化处理，可以保证输入空间划分的统一性，模型预测控制器加权准则可描述为采集当前时刻的值φ(k)及各子模型的调度函数值ρi(φ(k)):

该函数值可作为局部控制器的加权值.

3.3 算法步骤

非线性多模型由(15)式得到，设计各子预测控制器，全局控制量为各个子控制量加权和.多模型加权预测控制系统的结构如图1所示.具体步骤为：

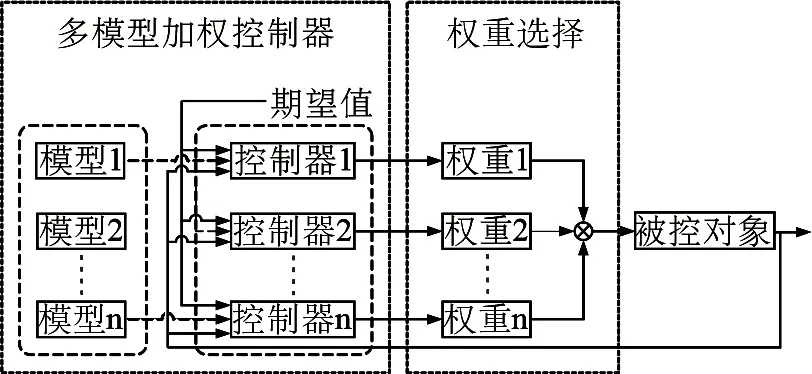
图1 多模型预测控制系统结构

第1步：采集实测的数据进行聚类，建立如(15)式所示的太阳能热发电集热子系统的多个非线性预测模型；

第2步：对各子模型设计相应的局部约束的MPC控制器；

第3步：在k时刻检测当前输入输出，并代入优化问题(20)，求解当前时刻局部控制增量Δui(k);

第4步：检测当前时刻工况参数φ(k)，由加权准则计算各局部控制量的加权值ρi(k);

第5步：计算控制增量

第6步：计算u(k)=u(k-1)+Δu(k)，作用于实际对象；

第7步：令k=k+1，返回第3步.

4 稳定性分析

引理1对于模型(12)，参数估计有如下性质[13]：

定理1文中设计的多模型切换控制算法，能够保证相应闭环系统的稳定性以及输出跟踪误差的收敛性，即

1){u(t)},{y(t)}有界;

2)ec(t)收敛.

证明(Ⅰ){u(t)},{y(t)}的有界性.

设太阳能热发电系统模型为

MPC的控制作用是在u(k)的作用下，使得k+1时刻的预测输出y(k+1)尽可能接近给定的期望值yr(k+1).

设(22)式中输出量的上、下限分别为ymax和ymin，则

ymin≤y(k+1)≤ymax

.

(23)

将(23)式代入(20)式可得

因此，多输出的约束可以用控制量变化量实现.

(Ⅱ)ec(t)的收敛性.

由控制误差e0(τ)=y(τ)-yr(τ)，得

|u(τ)|≤|ec(τ)|+|yr(τ)|≤|ec(τ)|+m,

其中|yr(τ)|≤m(0≤m<∞)为有界参数输入.从而

|φ(t-1)|≤M,

其中0≤M<∞,ec(t)=φT(t-1)θ(t-1)-yr(t).由于{u(t)},{y(t)}有界，所以{y(t)}有界；当Δu(k)趋近于0时，{yr(t)}趋近于{y(t)}，所以ec(t)收敛.】

5 结果分析

取甘肃西部已经投入并网发电的线性菲涅尔发电系统的参数进行验证分析.熔盐的流量取值在3～12 L·s-1,G=0.08 m,Af=0.65 m,η0=0.60,T=20 s,L=220 m，分别采用单模型和多模型进行验证分析.ρ=0.75,α=0.35，控制步长取1，控制加权系数取0.95，用实测的2023年6月15日数据进行验证，分析得到图2～9.图2为实测的太阳辐射强度，图3为入口温度变化，图4为室外温度变化，图5为单模型预测控制的结果，图6为控制增量，图7为6个模型切换的过程，图8和图9为多模型加权控制的结果和控制增量.

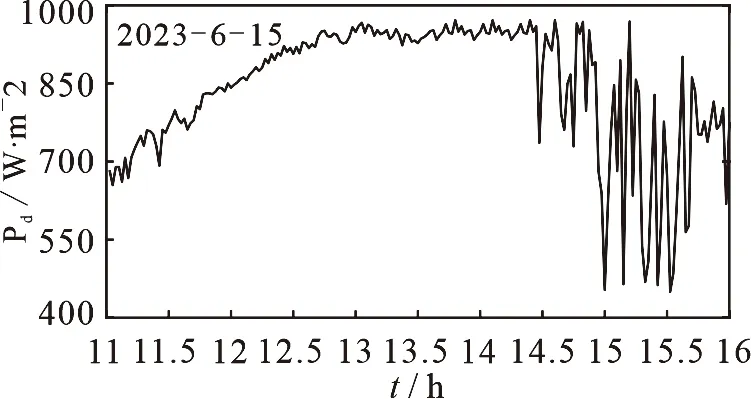
图2 太阳辐射强度

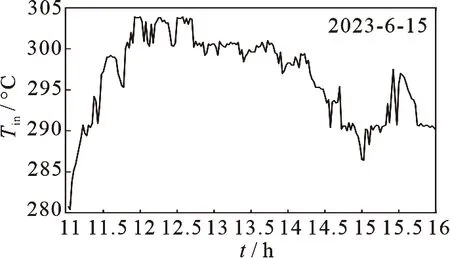
图3 入口温度

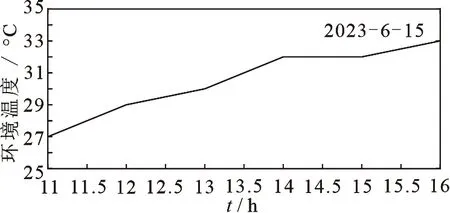
图4 当日温度变化

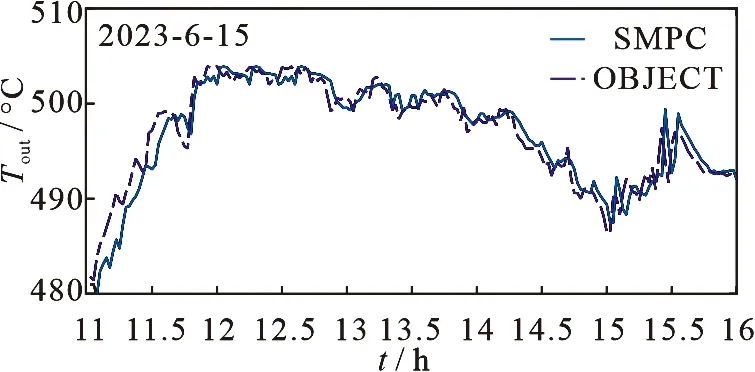
图5 单模型预测控制结果

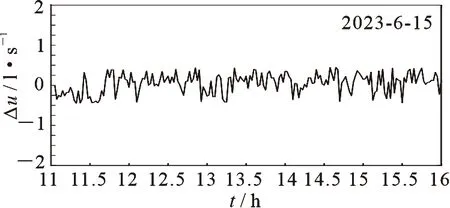
图6 单模型控制增量

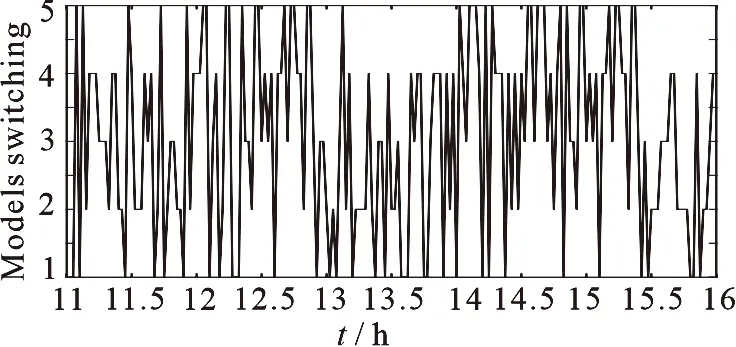
图7 控制过程模型选择

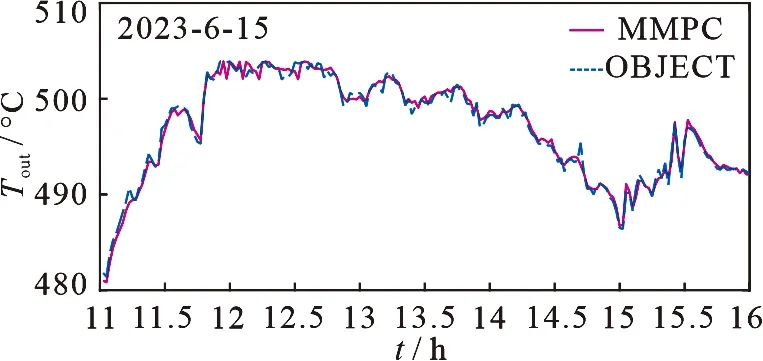
图8 加权多模型预测控制结果

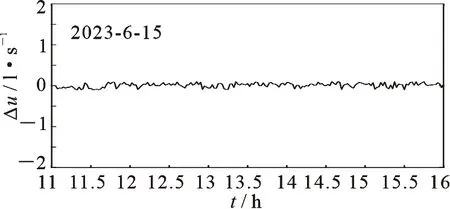
图9 加权多模型控制增量

集热管内采用熔盐为传热介质，熔盐密度、比热容分别为ρf=1 734J·(kg·K)-1,Cf=1 539.2 J·(kg·K)-1.

从图6和图9可以看出，多模型控制误差更小，控制的平稳性更好，SMPC得到MSE为1.487，MMPC得到的MSE为0.652.

6 结束语

利用加权准则设计了多模型预测控制器，应用实测的数据建立系统的多模型，并进行仿真研究；分别对实际系统做单模型预测控制和加权多模型预测控制研究，从实际采集的数据可以看出多模型控制精度更高；多模型比单模型预测控制的均方差明显要小，说明该方法能有效应用到太阳能热发电系统控制中.