离散情形下广义梯度与广义Skorohod积分的共轭关系

周玉兰，魏万瑛，柳翠翠，杨青青

(西北师范大学 数学与统计学院，甘肃 兰州 730070)

0 引言

近几年，离散时间正规鞅噪声泛函及其上量子分析理论受到广泛关注[5].2001年，Emery[5]讨论了这类泛函的混沌表示性质；2008年，Privault[6]用重积分形式讨论了Bernoulli泛函空间上的随机理论并给出了其在金融领域的应用；2011年，Wang等[7]构造了关于Bernoulli噪声平方可积泛函空间L2(Z)上的一组标准正交基，建立了N的有限幂集Γ上的平方可和函数空间L2(Γ)与Bernoulli噪声平方可积泛函空间L2(Z)的等距同构关系，从而给出了一个Privault理论的统一表达，并提出了量子Bernoulli噪声(简称QBN)的概念[8].Γ-指标集量子Bernoulli噪声{∂σ,∂*σ:σ∈Γ}是L2(Z)上的一列有界线性算子，满足典则反交换和等时可交换性质.文献[9]针对N上的非负函数h，在正规鞅平方可积泛函空间L2(Z)和正规鞅平方可积过程空间L2(Z×N)上提出了广义随机梯度h和广义Skorohod积分δh的概念，讨论发现，h可用点态湮灭算子列{∂k:k≥0}表示，而δh可用点态增生算子列{∂*k:k≥0}表示；文献[10]讨论了广义计数算子Nh关于QBN{∂k,∂*k:k≥0}的加权表示，并针对不同类型的非负函数h，在L2(Z)的不同稠密子空间上讨论广义计数算子Nh与h,δh之间的表示关系.

1 预备知识

设N表示非负整数集，Γ为N的有限幂集，即

Γ={σ:σ⊂N且#(σ)<+∞},

(1)

其中#(σ)表示集合σ的基数.显然Γ是一个可列集.对∀n≥0，令Γ(n)={σ∈Γ:#σ=n},{Γ(n):n≥0}是Γ的一个划分，Γ=∪n≥0Γ(n),∀n≥0.记[0,n]={0,1,2,…,n},Γn]={σ∈Γ:σ⊂[0,n]}，则Γn]是有限集，实际上，#Γn]=2n+1.设(Ω,F,P)是任意给定的概率空间，E是关于概率P的期望，用L2(Ω,F,P)表示(Ω,F,P)上平方可积复值随机变量所成的Hilbert空间.

设M=(Mn)n∈N是(Ω,F,P)上的离散时间正规鞅，应用M=(Mn)n∈N可构造离散时间过程Z=(Zn)n∈N如下:

Z0=M0,Zn=Mn-Mn-1,n≥1.

易证Z满足下面性质：

因此Z=(Zn)n∈N可看作离散时间正规噪声.

引理1[7]定义Z∅=1，且

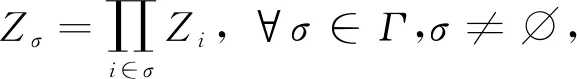
(2)

其中∅表示空集，则{Zσ:σ∈Γ(n)}是空间L2(Ω,F,P)的可数标准正交系.

为方便叙述，令H=L2(Ω,F,P)，若F是由{Zσ:σ∈Γ}生成的σ-代数，则H=L2(Z)=L2(Ω,F,P)为离散时间正规鞅平方可积泛函空间，其上内积和范数分别记作·,·和=·=.

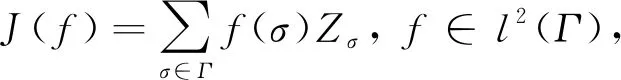
(3)

其中级数依L2(Ω,F,P)中范数收敛.

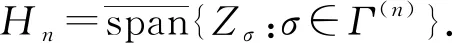
引理3[8](Wiener-It-Segal分解) 存在唯一的等距映射

(4)

∂kξ=J[f(*∪k)(1-1*(k))],

(5)

其中f=J-1(ξ)∈l2(Γ)，则∂k是H上的有界线性算子，且=∂k==1，特别地，

∂kZσ=1σ(k)Zσk, ∀σ∈Γ.

(6)

定义2[8]设k∈N，称∂k为k点处的湮灭算子，它的共轭算子∂*k称为k点处的增生算子.

引理4[8]设k∈N，则

∂*kξ=J[f(*k)1*(k)], ∀ξ∈H,

(7)

其中f=J-1(ξ)∈l2(Γ)，特别地，

∂*kZσ=(1-1σ(k))Zσ∪k, ∀σ∈Γ.

(8)

引理5[8]设k,l∈N,则

其中I是H上的恒同算子.

引理6[8]对∀k≥0，则∂*k∂k和∂k∂*k都是H的正交投影，并且

其中f=J-1(ξ)∈l2(Γ)；特别地，

用L2(Z×N)表示离散时间正规鞅M=(Mn)n≥0的平方可积过程全体所成的Hilbert空间，其中内积和范数分别为·,·和=·=L2(Z×N)，即对∀u=(uk)k≥0,v=(vk)k≥0∈L2(Z×N)，约定P+(N)表示N上的非负实函数，为N上可和序列(非负可和序列)全体所成Hilbert空间(子集).

定义3[11]设h∈P+(N)，定义算子h:L2(Z)L2(Z×N)如下:

称δh为关于h的广义Skorohod积分.

特别地，若h(k)≡1，则h=,δh=δ.

引理7[12]设h是N上的非负函数，则广义随机梯度h是L2(Z)中的稠定线性算子，δh是L2(Z×N)中的稠定闭线性算子，而h,δh有界当且仅当h是N上的平方可和函数，此时

引理8[9]Skorohod积分δ和随机梯度在其定义域内互为共轭算子，即有

定义4[9]对∀σ∈Γ,σ≠∅，定义L2(Z)上有界线性算子∂σ,∂*τ如下:

特别地，约定∂∅=O，而∂*∅=I，则称{∂σ,∂*τ:σ,τ∈Γ}为Γ指标集量子Bernoulli噪声，简记为Γ-QBN，这里σ={k1,k2,…,kn},τ={l1,l2,…,lm}，{∂σ∂*τ,∂*τ∂σ:σ,τ∈Γ}称为Γ-QBN混合积.

2 主要结果

下面定理1表明，对N上任意的非负实函数h,h的共轭算子恰是δh.

定理1设h∈P+(N)，则有

特别地，若h平方可和，则(13)式在全空间L2(Z)×L2(Z×N)上成立.

证明首先说明(13)式有意义.对∀ξ∈Domh,hξ∈L2(Z×N)，于是对u∈Domδh，由Cauchy-Schwartz不等式，有

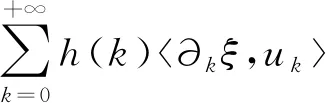
约定#g(∅)=0，称#g(·)为Γ上由g生成的广义计数测度.由(14)式可知，必存在L2(Z×N)到L2(Z)的算子T使得hξ,u=ξ,T(u).

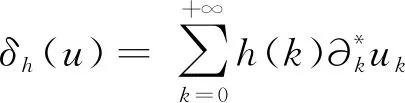
且该级数在L2(Z)中收敛.于是由内积连续性知，对∀ξ∈L2(Z)，有

而

故有

hξ,u=ξ,δh(u).

这表明(13)式成立.特别地，若h是N上非负平方可和函数，h和δh分别是L2(Z)和L2(Z×N)上有界线性算子，则上述共轭关系在L2(Z)×L2(Z×N)上成立.】

定理2设h∈P+(N)，则对∀σ,τ∈Γ，有

特别地，有

其中(15),(16)式中ξ∈Domh,u∈Domδh.当h平方可和时，上述共轭关系在L2(Z)×L2(Z×N)上成立，(16)式中若σ=∅，则h与δh相互共轭.特别地，h和量子Bernoulli噪声{∂k,∂*k:k≥0}的复合与同时刻对偶QBN和δh的复合也相互共轭.

证明首先证明，对h∈P+(N),h的定义域Domh是Γ-QBN{∂σ,∂*σ:σ∈Γ}的不变子空间.实际上，任取任取σ,τ∈Γ，由∂σ,∂*τ的有界性，有

这里

从而对任意l≥0，有

故

这表明∂σξ,∂*τξ∈Domh.由ξ∈Domh的任意性知，Domh是Γ-湮灭算子∂σ和τ-增生算子∂*τ的不变子空间，进而Domh是Γ-QBN混合积{∂σ∂*τ,∂*τ∂σ:σ,τ∈Γ}的不变子空间，即h∂σ∂*τ,h∂*τ∂σ在Domh上有意义，于是有

这里在第三个等号中令α=(ω∪τ)σl，则ω=(α∪σ)∪lτ，故(15)的第一式成立，(h∂σ∂*τ)*=∂τ∂*σδh，且

同理可证(15)的第二式也成立，即

h∂*τ∂σξ,u=ξ,∂*σ∂τδh(u).

在(15)式中取σ=∅或τ=∅可得(16)式成立.

若h是N上非负平方可和函数，则对应的h和δh分别是L2(Z)和L2(Z×N)上有界线性算子，从而由前述证明可得(15),(16)式在全空间L2(Z)×L2(Z×N)上成立，进而在(15),(16)式中取σ,τ∈Γ，则h和Γ-QBN的复合与δh和共轭QBN的复合相互共轭.】

注1定理2中，σ-湮灭算子∂σ和τ-增生算子∂*τ不可交换.

下面命题1表明，当σ与τ满足某种特殊条件时，复合共轭关系中∂σ与∂*τ指标顺序不变.

命题1设h∈P+(N),σ,τ∈Γ，且σ∩τ=∅，则

这里ξ∈Domh,u∈Domδh.

证明设h∈P+(N)，则对任意σ,τ∈Γ,l≥0，由定理2，有

由于σ∩τ=∅，故有(1-1ω(τ))1(ω∪τ)(σ)1(ω∪τ)σ(l)=(1-1ωσ(τ))1ω(σ)1(ωσ)∪τ(l)，从而对∀l≥0，有

从而

h∂σ∂*τξ=h∂*τ∂σξ，

故由(15)式可得

同理可证

注2由命题1的证明知，当σ∩τ=∅时，σ-湮灭算子∂σ与τ-增生算子∂*τ可交换，即

∂σ∂*τ=∂*τ∂σ.

下面定理3表明等时异型Γ-QBN“夹逼”h和δh的复合时，复合算子可“跳出夹逼”，此时又“增生”出等时型复合Γ-QBN{∂σ∂*σ,∂*σ∂σ:σ∈Γ}的数乘算子，且当增生在左、湮灭在右时，∂*σ∂σ的系数为负，而湮灭在左、增生在右时，∂σ∂*σ的系数为正.

定理3设h∈P+(N),σ∈Γ，则

上式在L2(Z)的稠密线性子空间Dh上成立，这里

证明首先说明h(Dh)⊂Domδh.实际上，任取ξ∈Dh,hξ=(h(l)∂lξ)l≥0，令ul=h(l)∂lξ,∀l≥0，则有

故由ξ∈Dh的任意性知，h(Dh)⊂Domδh，从而(18),(19)式左端复合算子δh∘h有意义.又由于

故

对g∈P+(N)，其诱导了Γ上广义计数测度#g，对任意σ⊂Nsuppg有#g(σ)=0.对支撑不是全空间N的h∈P+(N)，一类特殊Γ-QBN“夹逼”复合δh∘h时，δh∘h直接“跳出夹逼”，特别地，对特殊的QBN，不同顺序的QBN“夹逼”δh∘h时，消除了QBN的作用.

命题2设h∈P+(N)且supph≠N，则

特别地，有

证明由定理3的证明可知，(18),(19)式成立，而当σ⊂Nsupph时#h2(σ)=0，从而等时Γ-QBN“夹逼”δh∘h时，∂*σ∂σ,∂σ∂*σ的系数为0，于是(20)式成立.而当k⊂Nsupph时，∂*k,∂k满足等时CAR，∂*k∂k+∂k∂*k=I，从而

对h∈P+(N),h与δh的复合与等时型混合Γ-QBN有某种交换性可推广到更一般情形.Γ-QBN混合积{∂*τ∂σ,∂τ∂*σ:σ,τ∈Γ}及其共轭“夹逼”δh∘h时，δh∘h可“跳出夹逼”，且出现混合积复合的线性函数，其系数是h2生成测度在σ与τ不交部分上测度值的组合.

定理4设σ,τ∈Γ,h∈P+(N)，则

以上两式在Dh上成立.

证明任取ξ∈Dh，则

这表明(22),(23)式成立.】

下面给出针对N上非负函数h，Γ-QBN混合积{∂*σ∂τ,∂τ∂*σ:σ,τ∈Γ}“夹逼”δh∘h时，其复合δh∘h直接“跳出夹逼”，QBN等时混合积及其共轭“夹逼”δh∘h时，消除了QBN的作用.

推论1设σ,τ∈Γ,h∈P+(N),

1)若#h2(στ)=#h2(τσ)，则

(∂*τ∂σδh)∘(h∂*σ∂τ)=δh∘h∂*τ∂σ∂*σ∂τ.

2)若στ,τσ⊂Nsupph，则

(∂σ∂*τδh)∘(h∂τ∂*σ)=δh∘h∂σ∂*τ∂τ∂*∂.

推论2设h∈P+(N),k≥0，则

特别地，有

∂*k∂kδh∘h∂*k∂k+∂k∂*kδh∘h∂k∂*k=δh∘h.